中国数字普惠金融的发展现状及收敛性研究——基于logt检验方法的考察

王善高 陈燕齐 田 旭

一、引言与文献综述

随着互联网、云计算等信息技术发展，金融服务与信息技术开始逐渐交叉融合(1)黄益平、黄卓：《中国的数字金融发展：现在与未来》，《经济学(季刊)》2018年第4期。。在此背景下，深度融合通信技术与普惠金融服务的数字普惠金融应运而生。作为一种新的金融模式，数字普惠金融能够克服传统金融对物理网点的依赖，具有更大的地理穿透力和低成本优势(2)何宏庆：《数字普惠金融风险：现实表征与化解进路》，《兰州学刊》2020年第1期。。在G20峰会上，中国政府参与制定的《G20数字普惠金融高级原则》明确了数字普惠金融发展方向。在政府引导、信息技术支撑以及各类金融服务主体参与下，数字普惠金融在全国各地如雨后春笋般迅猛发展。政府发展普惠金融的初衷是为社会所有阶层和群体提供金融服务，特别是为贫困地区、少数民族地区、偏远地区以及残疾人和其他弱势群体提供金融服务(3)尹应凯、侯蕤：《数字普惠金融的发展逻辑、国际经验与中国贡献》，《学术探索》2017年第3期。(4)郑雅心：《数字普惠金融是否可以提高区域创新产出：基于我国省际面板数据的实证研究》，《经济问题》2020年第10期。。由于经济发展水平、经济结构、传统金融发展水平、互联网发展程度等存在差异，我国各地区普惠金融服务发展不均衡(5)郭峰、王靖一、王芳等：《测度中国数字普惠金融发展：指数编制与空间特征》，《经济学(季刊)》2020年第4期。，这使得普惠金融的初衷难以实现。那么，作为普惠金融的新业态，数字普惠金融能否突破传统金融的不足，打破地域限制，实现均衡发展呢？这一问题的解答关乎数字普惠金融能否实现协同发展，而要想回答这一问题，就需要掌握数字普惠金融的现状及其在未来的发展趋势。

为解答上述问题，许多学者基于北京大学数字金融研究中心课题组发布的中国数字普惠金融指数对中国数字普惠金融的分布差异及收敛趋势进行了研究，如孙英杰和林春采用该数据分析了中国数字普惠金融的绝对β收敛和条件β收敛，发现我国数字普惠金融发展同时存在绝对β收敛和条件β收敛(6)孙英杰、林春：《中国普惠金融发展的影响因素及其收敛性——基于中国省级面板数据检验》，《广东财经大学学报》2018年第2期。。梁榜和张建华采用该数据考察了中国城市数字普惠金融发展的收敛情况，发现东部、中部和西部地区的数字普惠金融发展存在σ收敛、绝对β收敛和条件β收敛(7)梁榜、张建华：《中国城市数字普惠金融发展的空间集聚及收敛性研究》，《财经论丛》2020年第1期。。张德钢和朱旭森采用该数据考察了中国九大城市群数字普惠金融发展的收敛情况，发现九大城市群数字普惠金融发展具有σ收敛特征和β收敛特征(8)张德钢、朱旭森：《中国九大城市群数字普惠金融发展的时空差异及动态演进》，《当代经济管理》2020年第12期。。此外，王雪和何广文、张龙耀和邢朝辉等学者还采用该数据考察了中国县域数字普惠金融发展的σ收敛情况和β收敛情况(9)王雪、何广文：《中国县域普惠金融发展的空间非均衡及收敛性分析》，《现代经济探讨》2020年第2期。(10)张龙耀、邢朝辉：《中国农村数字普惠金融发展的分布动态、地区差异与收敛性研究》，《数量经济技术经济研究》2021年第3期。。

上述研究在理论与实证方面均作了有益探讨，然而，还存在以下不足：第一，在分析数字普惠金融的收敛趋势时，大都聚焦于数字普惠金融指数本身，忽视了数字普惠金融不同维度的分指数。事实上，北京大学数字普惠金融指数，除了包含数字普惠金融指数外，还包含不同维度的分指数，如覆盖广度指数、使用深度指数和数字化程度指数等，这些分指数代表了数字普惠金融的不同方面。仅分析数字普惠金融指数的收敛趋势，只能从整体上把握数字普惠金融的发展趋势，不能细致展现数字普惠金融指数内部是如何变化的，不利于找出引起数字普惠金融异动的因素。第二，在收敛检验方法上，大多采用σ收敛检验和β收敛检验。然而，Phillips等指出σ收敛检验和β收敛检验均存在一定偏误(11)Phillips P C B., Sul D., “Transition modeling and econometric convergence tests”, Econometrica，Vol. 75, no.6, 2007, pp. 1771-1855.。对于σ收敛，如果数据存在诸如布朗运动、列维游走等不稳定现象，方差的自然增长会使得σ收敛检验存在严重偏误。对于β收敛，Lichtenberg指出存在这样一种情形，就是部分省份的初始水平较低，但它拥有较快的增长速度，以至于在末期的时候超过了初始水平较高的省份，导致末期两省之间的差距大于初期的差距(12)Lichtenberg F R., “Testing the convergence hypothesis”, Review of Economics and Statistics，Vol. 76, no.3, 1994, pp. 576-579.，即出现了所谓的“赶超”现象，此时用Barro提出的方程检验β收敛所得出的结论是错误的(13)Barro R J., Sala-i-Martin X., “Convergence”, Journal of Political Economy，Vol. 100, no.2,1992,pp.223-251.。此外，σ收敛检验和β收敛检验均属于“非此即彼”的检验，即要么存在收敛，要么不存在收敛，完全忽视了俱乐部收敛。事实上，当数据总体不收敛时，依然可能存在收敛的俱乐部，而σ收敛检验和β收敛检验均忽视了俱乐部收敛现象。

针对现有研究的不足，本研究拟作出以下改进：第一，研究内容上，在分析数字普惠金融的收敛趋势时，除了对数字普惠金融指数进行收敛性分析外，还对数字普惠金融三个一级分指数进行收敛性分析，以期识别出数字普惠金融不同维度分指数的变化情况。第二，研究方法上，在进行收敛检验时，采用logt检验方法(也称俱乐部收敛检验)。该检验方法允许数据存在各种不同的时间趋势和个体异质性，而且还能在总体样本不收敛时，进一步考察样本是否存在俱乐部收敛。有鉴于此，本研究拟基于北京大学数字金融研究中心课题组发布的2011—2020年中国数字普惠金融指数，采用数理统计方法从时间和空间两个维度梳理中国数字普惠金融的现状，并采用logt检验方法分别考察中国数字普惠金融指数及其三个一级分指数的收敛情况，以期准确识别出中国数字普惠金融的动态演进特征，为各地区的数字普惠金融实现均衡发展提供理论指导。

二、研究方法

(一)传统收敛检验

1. σ收敛检验

σ收敛指的是不同地区间的分散程度随时间推移而趋于下降。目前，检验σ收敛的指标有很多，如标准差、变异系数、基尼系数和泰尔指数等。其中，变异系数因测算简单，且能消除测量尺度和量纲的影响，被学者们广泛用于σ收敛检验中(14)唐文健、李琦：《中国区域俱乐部收敛的形成与变化——基于参数与非参数估计的研究》，《华东经济管理》2008年第9期。。本研究也采用变异系数来考察数字普惠金融指数及其三个一级分指数的σ收敛情况。变异系数计算公式如下：

(1)

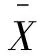
2. β收敛检验

β收敛指的是初始水平较低的地区因拥有较高的增长率而在未来某个阶段赶上那些初始水平较高的地区，最后达到相同的稳态水平。需要说明的是，β收敛分为两类：一是绝对β收敛；二是条件β收敛。两者的基本回归方程大体一致，区别在于绝对β收敛认为即使不加入控制变量，不同地区间也会呈现收敛趋势；而条件β收敛认为只有加入控制变量，不同地区间才会呈现收敛趋势。为简化分析，我们仅进行绝对β收敛检验。借鉴Barro的思路(15)Barro R J., Sala-i-Martin X., “Convergence”, Journal of Political Economy，Vol. 100, no.2, 1992, pp. 223-251.，构造如下的实证方程进行检验：

[ln(Xi,t+T)-ln(Xi,t)]/T=α+βln(Xi,t)+εit

(2)

其中，i和t为省份和年份，X为相关指数，T为时间跨度，ε为随机误差，α、β为待估计系数。

(二)俱乐部收敛检验

1. 俱乐部收敛检验理论的介绍

由于面板数据包含了时间特征和个体特征，因此对于任意一个面板数据我们在理论上都可以将其分解为两部分。假设面板数据为Xit，分解公式如下：

Xit=δit×μt

(3)

其中，Xit为任意一个面板数据，这里指数字普惠金融指数及其三个一级分指数；δit为时间变化因子的载荷系数；μt为所有个体的共同因子。需要说明的是，公式(3)可以看作是一个动态因子模型，其中，μt反映了一些确定性或随机性的趋势行为，而δit测度了Xit和μt之间的特殊距离。

进一步地，时间变化因子的载荷系数δit可以用一个半参数方程表示，公式如下：

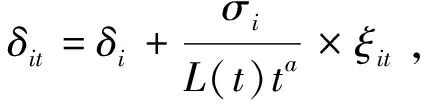
(4)

其中，δit为时间变化因子的载荷系数，δi为不随时间变化的固定成分，ξit为随时间变化的可变成分，L(t)是一个关于时间t的函数。主要用于消除方差随时间发展而出现的自然增长趋势，从而将非平稳面板数据转化为平稳面板数据。需要指出的是，如果面板数据本身就是平稳的，那么方差就不会随时间发展而出现自然增长趋势，此时L(t)可以忽略不计。由公式(4)可知，当面板数据是平稳面板数据的时候，如果a≥0且t→+∞，δit就会收敛于δi。进一步地，如果δi=δ，即所有个体的共同因子都一样，在此情形下，如果a≥0，则所有个体都将收敛于相同的均衡状态。如此一来，面板数据Xit是否收敛就可以通过检验a是否大于等于0来判断。

在实证研究中，我们可以通过以下方法来检验面板数据Xit是否收敛。原假设为H0：δi=δ，且a≥0。假设检验可以通过以下的logt回归模型实现，公式如下：

(5)

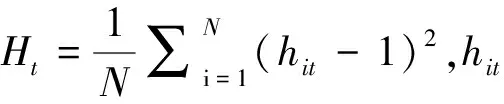
2. 俱乐部收敛检验的分析步骤

为系统展示俱乐部收敛检验方法，接下来，我们将对俱乐部收敛检验的操作步骤作简要介绍。具体步骤如下：

第二步：确定核心组成员。按照公式(5)依次对均值最高的k个个体进行回归，计算出logt的t检验值tk。如果计算出的tk值<-1.65，就不再回归，因为tk值<-1.65说明在5%的水平上显著，表明我们已经找到了核心组成员。此时，需要在已经计算出的tk值中找出最大值，与该值对应的k*即为核心收敛组成员个数。在上述实证过程中，可能会出现如下的情形：情形一，如果所有的tk值>-1.65，说明面板数据中所有个体都收敛于同一个组，这意味着总体样本收敛，此时存在一个收敛俱乐部。情形二，如果均值最高的2个个体logt的t检验值tk<-1.65，说明这2个个体不是核心组成员，此时需要剔除均值最高的个体，并对余下的个体重复上述步骤，即重新进行logt检验。如此往复循环，直至找出tk值>-1.65的核心组。如果任意连续个体对应的t检验值tk均<-1.65，说明不存在核心组，这意味着总体样本不收敛。

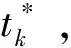
三、数据来源与变量说明

(一)数据来源

本研究数据来源于北京大学数字金融研究中心课题组于2021年4月最新发布的2011—2020年“北京大学数字普惠金融指数”。该指数是北京大学数字金融研究中心利用蚂蚁金服的微观数据，从数字金融覆盖广度、数字金融使用深度和数字金融数字化程度三个维度共计33个具体指标加权汇编而成。同时，该指数覆盖了全国31个省份337个地级以上城市和约2800个县域城市，具有样本量大、覆盖范围广、连续性好、可比性强的特点，能较为客观、全面地反映中国数字普惠金融的实际发展状况。

(二)变量说明

北京大学数字金融研究中心课题组公布的“北京大学数字普惠金融指数”，除了包含数字普惠金融指数外，还包含不同维度的分指数，如一级维度指数、二级维度指数等。数字普惠金融指数是由三个维度的一级分指数构建而成，而不同维度的一级分指数也是由若干维度的二级分指数构建而成。本研究选取其中的数字普惠金融指数及其三个一级分指数进行研究。具体说明如下：(1)数字普惠金融指数：该指数包含三个一级分指数，分别是覆盖广度指数、使用深度指数和数字化程度指数。(2)一级分指数：①覆盖广度指数，该指数仅包含账户覆盖率一个业务维度。②使用深度指数，该指数包含支付、货基、信用、保险、投资和信贷六个业务维度。③数字化程度指数，该指数包含信用化、便利化、实惠化和移动化四个业务维度。

四、实证结果与分析

(一)数字普惠金融的现状分析

1. 时间维度

图1展示了2011—2020年数字普惠金融指数及其三个一级分指数均值的折线图。由图可知，2011—2020年，我国数字普惠金融指数均值由40.00变为341.22，增长了7.5倍，年均增长速度为23.91%，呈现出明显的增长趋势。出现这种现象的可能原因有：一方面，在数字普惠金融发展的初期，其借助互联网、云计算等现代信息通信技术在全国各地如雨后春笋般地迅猛发展。另一方面，国务院印发的《推进普惠金融发展规划纲要(2016—2020年)》，确立了推进普惠金融发展的指导思想、基本原则和发展目标。在此背景下，各地政府先后出台了一些促进普惠金融发展的政策措施，而且在政府的引导下，各类金融服务主体也参与到普惠金融的建设中，因此我国的数字普惠金融业务实现了快速发展。

从分指数来看，2011—2020年，覆盖广度指数、使用深度指数、数字化程度指数的均值分别由34.28、46.93、46.32变为326.44、338.05、395.82，分别增长了8.5倍、6.2倍和7.5倍，年均增长速度依次为25.28%、21.83%、23.93%，均呈现出明显的增长趋势。值得注意的是，覆盖广度指数、使用深度指数、数字化程度指数的增长具有明显的阶段性特征。具体而言，在2011—2015年期间，数字普惠金融的数字化程度增长最快，覆盖广度次之，而使用深度增长最慢。在2015—2018年期间，数字普惠金融的使用深度增长最快，覆盖广度次之，而数字化程度增长最慢。在2018—2020年期间，数字普惠金融的使用深度增长最快，而覆盖广度和数字化程度的增长速度差不多。由此可见，使用深度指数增长是数字普惠金融指数增长的重要驱动力，这可能是因为当数字普惠金融的覆盖广度达到一定程度以后，数字普惠金融发展的动力必然落到了数字化程度和使用深度上，而数字化程度的发展需要依托现代信息通信技术，技术的升级不是一蹴而就的行为，因此数字化程度指数增长就相对缓慢，所以使用深度指数增长就成了数字普惠金融指数增长的重要驱动力。

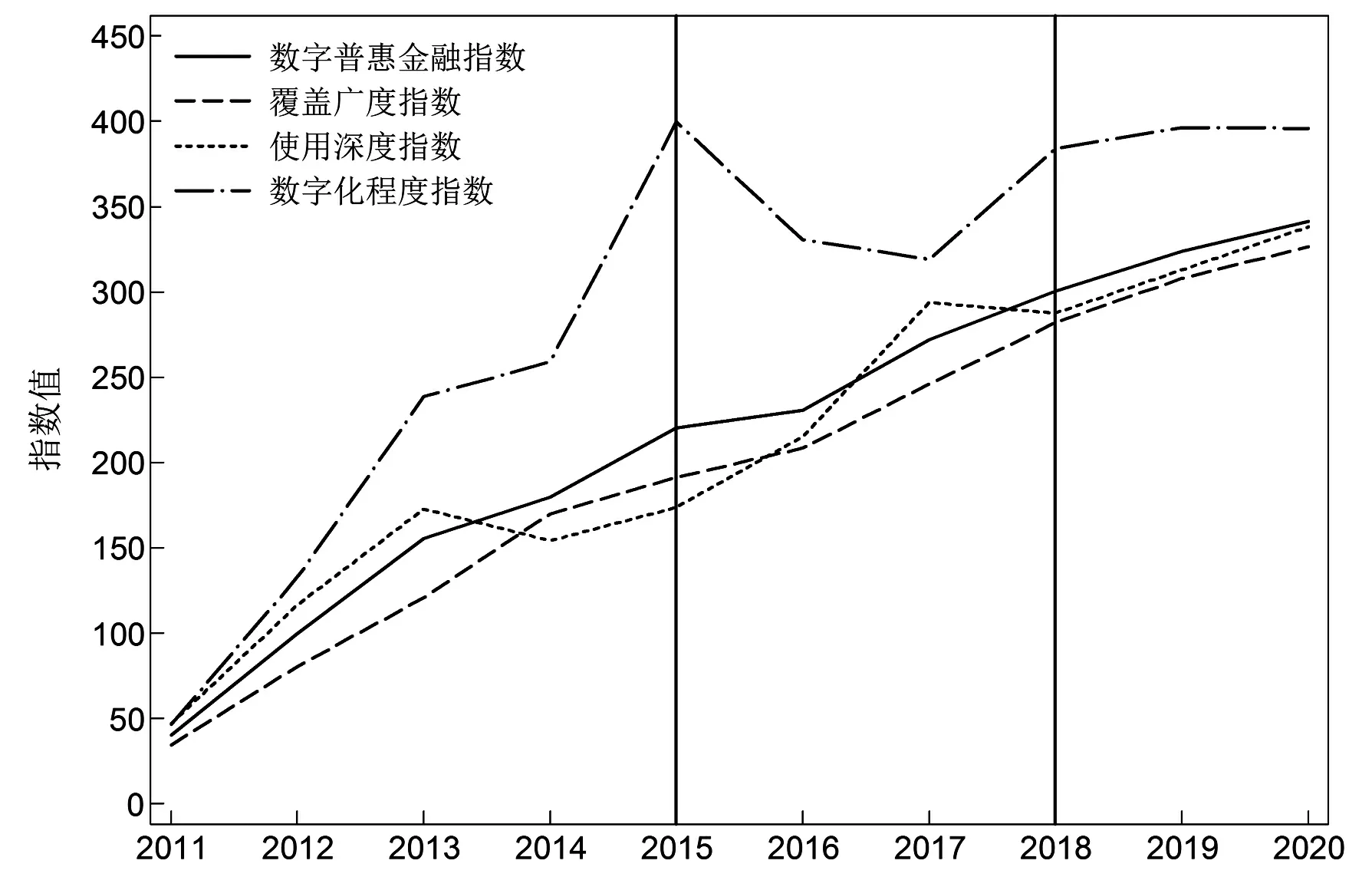
图1 2011—2020年数字普惠金融指数及其三个一级分指数均值的折线图

2. 空间维度

图2展示了2011—2020年不同地区数字普惠金融指数及其三个一级分指数均值的柱状图。由图可知，东部地区的数字普惠金融指数要高于中部地区和西部地区，而中部地区的数字普惠金融指数又要高于西部地区，说明我国的数字普惠金融业务发展存在明显的地区差异。与此同时，我们发现在每一个区域内部，不同省份的数字普惠金融指数均存在不同程度的两极分化现象，即出现了所谓的“高的高、低的低”现象，且这种现象在东部地区体现得尤为明显。以东部地区为例，数字普惠金融指数得分最高的上海市是得分最低的河北省的1.39倍。当然，这也是在提醒我们，要注重数字普惠金融业务发展的均衡性，因为“木桶理论”告诉我们，一只水桶能装多少水取决于它最短的那块木板(16)王善高、田旭、徐章星：《中国生猪养殖的最优规模研究——基于不同效率指标的考察》，《统计与决策》2020年第17期。，所以在每一个区域内部，不能只看那些数字普惠金融业务发展得较好的省份，还要对那些数字普惠金融业务发展得不好的省份投入更多的关注。

从分指数来看，覆盖广度指数和使用深度指数也存在东部地区高于中、西部地区，而中部地区又高于西部地区的现象，且这种现象在使用深度指数上体现得尤为明显。不同的是，数字化程度指数在东部地区、中部地区、西部地区虽有差异，但差异相对较小。出现这种现象的可能原因是，数字化程度指数的发展不受地理条件的限制，主要依赖于现代信息通信技术，因此即使是条件相对艰苦的西部地区，只要有智能手机等通信基础设施，数字化程度指数也会处于相对较高的水平，而现代信息通信技术的传播与扩散又具有较强的穿透性和快捷性，这在一定程度上会提升西部地区的数字化程度指数，因此东部地区、中部地区、西部地区数字化程度指数的差异不大。

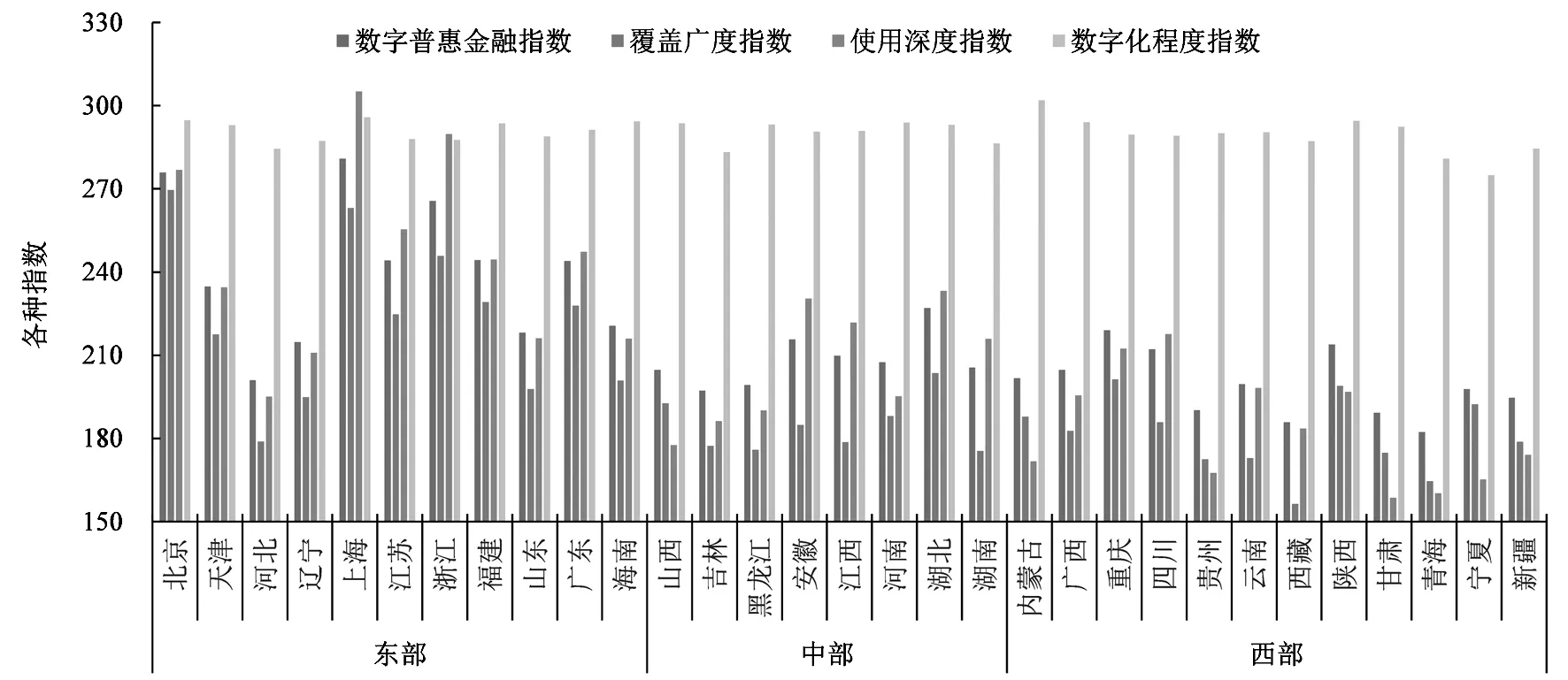
图2 2011—2020年不同地区数字普惠金融指数及其三个一级分指数均值的柱状图

(二)数字普惠金融的传统收敛检验

1. σ收敛检验

图3展示了数字普惠金融指数及其三个一级分指数变异系数的折线图。由图可知，数字普惠金融指数、覆盖广度指数、使用深度指数、数字化程度指数的变异系数在总体上均存在下降趋势，说明数字普惠金融指数、覆盖广度指数、使用深度指数、数字化程度指数的分散程度在总体上有缩小趋势，这意味着数字普惠金融指数及其三个一级分指数均存在σ收敛趋势。与之相似，焦云霞、梁榜和张建华、张德钢和朱旭森等学者的研究中也发现了类似的现象(17)焦云霞：《中国数字普惠金融发展的空间集聚与收敛性研究》，《金融发展》2020年第2期。(18)梁榜、张建华：《中国城市数字普惠金融发展的空间集聚及收敛性研究》，《财经论丛》2020年第1期。(19)张德钢、朱旭森：《中国九大城市群数字普惠金融发展的时空差异及动态演进》，《当代经济管理》2020年第12期。。值得注意的是，除覆盖广度指数的变异系数有一直下降的趋势以外，数字普惠金融指数、使用深度指数以及数字化程度指数变异系数在2017—2020年均出现了不同程度的上升趋势，说明覆盖广度指数的分散程度一直在缩小，而数字普惠金融指数、使用深度指数和数字化程度指数的分散程度在2017年以后有略微扩大的趋势，这意味着数字普惠金融的覆盖广度在日渐趋同，而数字普惠金融的使用深度和数字化程度有朝着不同方向发展的势头。考虑到数字普惠金融指数是由覆盖广度指数、使用深度指数和数字化程度指数加权汇编而成，因此我们推断数字普惠金融地区收敛性反弹的主要原因是使用深度指数和数字化程度指数在反弹。

图3 数字普惠金融指数及其三个一级分指数变异系数折线图

2. β收敛检验

表1汇报了数字普惠金融指数及其三个一级分指数绝对β收敛检验的估计结果。首先，看模型拟合情况，模型1、模型2、模型3、模型4的R-squared值(拟合优度)依次为0.974、0.992、0.928、0.982，均相对较大，说明4个模型拟合得较好。其次，看绝对β收敛情况，ln(数字普惠金融指数)、ln(覆盖广度指数)、ln(使用深度指数)、ln(数字化程度指数)的估计系数依次为-0.073、-0.089、-0.068、-0.113，且都在1%的水平上显著，说明数字普惠金融指数、覆盖广度指数、使用深度指数以及数字化程度指数均存在绝对β收敛趋势，这意味着在各种可能因素的作用下，数字普惠金融指数、覆盖广度指数、使用深度指数以及数字化程度指数初始水平较低的省份因拥有较高的增长速度而朝着初始水平较高的省份追赶，并且随着时间推移，可以预期初始水平较低的省份和初始水平较高的省份在未来某个阶段会收敛于相同的稳态水平。与之相似，胡宗义等、沈丽等、林春等等学者的研究中也发现了类似的现象(20)胡宗义、丁李平、刘亦文：《中国普惠金融发展的空间动态分布及收敛性研究》，《软科学》2018年第9期。(21)沈丽、张好圆、李文君：《中国普惠金融的区域差异及分布动态演进》，《数量经济技术经济研究》2019年第7期。(22)林春、康宽、孙英杰：《中国普惠金融的区域差异与极化趋势：2005-2016》，《国际金融研究》2019年第8期。。

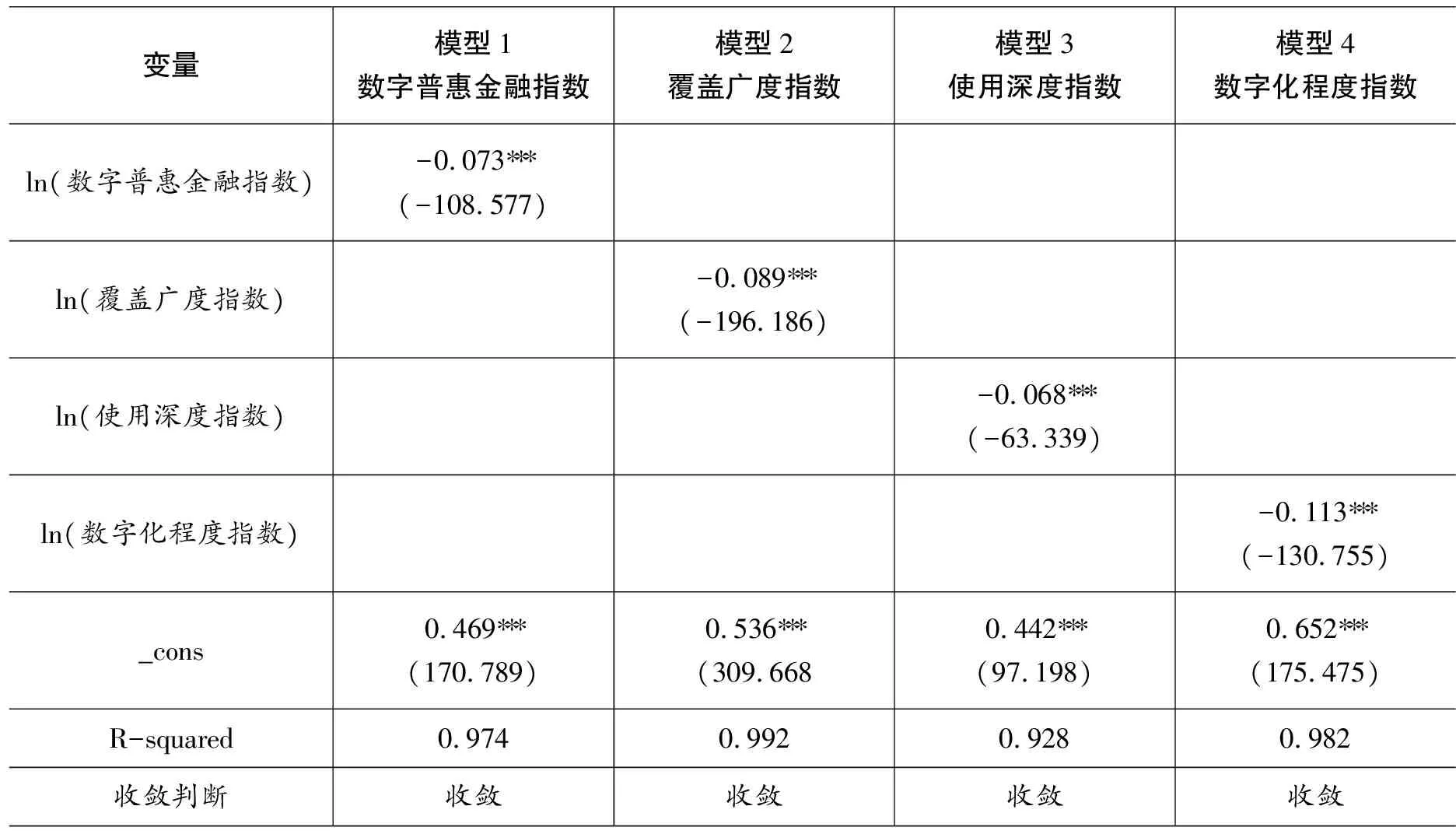
表1 数字普惠金融指数及其三个一级分指数的绝对β收敛检验

(三)数字普惠金融的俱乐部收敛检验

上文的研究结果显示，数字普惠金融指数、覆盖广度指数、使用深度指数、数字化程度指数同时存在σ收敛趋势和绝对β收敛趋势。然而，传统的σ收敛检验方法和β收敛检验方法均存在一些不足之处。对于σ收敛检验，如果数据在不同阶段的变化趋势不一致，就无法明确判断数据是否存在σ收敛。此外，如果数据本身就是不稳定的，方差的自然增长也会使σ收敛出现误导性。对于β收敛检验，存在这样一种情形，就是部分省份的初始水平较低，但它拥有较快的增长速度，以至于在末期的时候超过了初始水平较高的省份，导致末期两者之间的差距大于初期的差距，这就会使得β收敛检验出现偏误。更关键的是，σ收敛检验和β收敛检验均忽视了俱乐部收敛。

为弥补传统收敛检验存在的不足，本研究采用logt检验来考察数字普惠金融指数、覆盖广度指数、使用深度指数、数字化程度指数的收敛情况。需要说明的是，logt检验的分析步骤较多，而且涉及大量的计算，因此logt检验相对繁杂。庆幸的是，中国经济学者Kerui Du开发出了一套完整的用于logt检验的stata指令包，该指令包包含pfilter、logtreg、psecta、scheckmerge、imergeclub等5部分(23)Du K., “Econometric convergence test and club clustering using stata”, The Stata Journal， Vol. 17, no.4, 2018, pp. 882-900.。其中，指令pfilter用于消除面板数据存在的时间趋势，指令logtreg用于总体收敛检验，指令psecta用于俱乐部收敛检验，指令scheckmerge用于检查相邻的两个收敛俱乐部能否合并成更大的收敛俱乐部，指令imergeclub用于展示合并以后的收敛俱乐部。得益于专家学者的研究以及学术成果的开放共享，以上指令均属于公开指令，均可在stata软件中直接下载使用，我们将借助上述指令进行logt检验。

1. 总体收敛检验

考虑到面板数据可能存在时间趋势，我们首先用pfilter指令基于HP滤波法对数字普惠金融指数、覆盖广度指数、使用深度指数和数字化程度指数进行了平滑处理。然后，基于平滑处理后的数据，利用logtreg指令检验了数字普惠金融指数及其三个一级分指数的总体收敛趋势，结果见表2。结果显示，数字普惠金融指数、覆盖广度指数、使用深度指数log(t)检验的t统计值均>-1.65，说明数字普惠金融指数、覆盖广度指数、使用深度指数在全国范围内趋于收敛，而数字化程度指数log(t)检验的t统计值<-1.65，说明数字化程度指数不存在总体收敛趋势。出现这种现象的可能原因有：第一，数字普惠金融指数收敛的可能原因是，数字金融不再依赖传统的金融基础设施和物理网点，而是借助互联网、大数据和云计算等现代信息通信技术，以及数字金融产品创新拓展了普惠金融的触达能力和服务范围，降低了金融服务的成本，实现了金融机构和客户的共赢。由于优势明显，数字普惠金融在全国各地如雨后春笋般地迅猛发展。在此期间，全国各地数字普惠金融的覆盖广度、使用深度、数字化程度均得到了极大提高，所以数字普惠金融指数在全国范围内趋于收敛。第二，覆盖广度指数收敛的可能原因是，覆盖广度通俗讲就是覆盖了多少人群，而覆盖范围是有边界的，随着各地客户市场逐渐饱和，数字普惠金融的覆盖范围会逐渐达到边界，因此各地数字普惠金融的覆盖广度在全国范围内趋于收敛。第三，使用深度指数收敛的可能原因是，使用深度通俗讲就是使用频率，由于数字普惠金融优势明显，因此使用的人会越来越多，但消费习惯会使人们的使用频次趋于稳定，这在一定程度上会促使使用深度指数在全国范围内趋于收敛。第四，数字化程度指数发散的可能原因是，伴随着智能手机的普及，数字普惠金融的数字化程度迅速提升，然而，现代移动通信技术不是一成不变的，随着我国科学技术水平的不断提升，移动通信技术也得到了快速发展，因此各地的现代通信技术也呈现出了差异化的态势，这在一定程度上会促使各地数字普惠金融的数字化程度朝着不同的方向发展，最终使得数字化程度指数发散。

值得注意的是，数字化程度指数不存在总体收敛趋势，这一结论在一定程度上佐证了图1的结果，即在2017年以后使用深度指数和数字化程度指数的变异系数开始出现不同程度的上升趋势。当然，可能此时仅有数字化程度指数的发散性显现出来了，而使用深度指数的发散性还没有完全显现出来，因此使用深度指数在全国范围内还是趋于收敛的。但我们相信，随着时间的推移，使用深度指数的发散性也会逐步显现出来。事实上，当用户规模达到一定级别以后，数字普惠金融指数的增长点只可能来自使用深度和数字化程度，而这两点也会是造成数字普惠金融出现地区差异的重要原因。

由此可见，logt检验对传统的σ收敛检验和β收敛检验的结果提出了挑战，表明σ收敛检验和β收敛检验在理论和实践中存在一定的偏误，如果完全依赖σ收敛检验和β收敛检验可能会遗漏部分潜在信息，从而得到片面甚至是有偏误的研究结论。

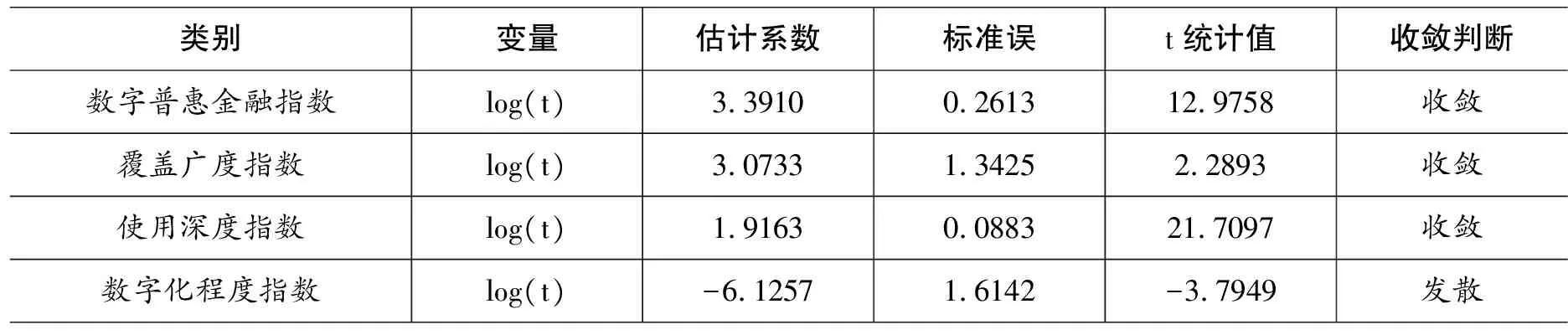
表2 数字普惠金融指数及其三个一级分指数的总体收敛检验

2. 收敛俱乐部检验

上文指出，即使总体不收敛，不同省份也完全有可能收敛于几个区域性的俱乐部，呈现出俱乐部收敛态势。进一步地，利用stata指令psecta、scheckmerge和imergeclub考察了数字普惠金融指数、覆盖广度指数、使用深度指数和数字化程度指数的俱乐部收敛情况，结果见表3。结果显示：第一，数字普惠金融指数、覆盖广度指数以及使用深度指数均收敛于一个俱乐部，即在全国范围内趋于收敛，这与表2的研究结果相一致。第二，数字化程度指数存在俱乐部收敛趋势，而且收敛于两个俱乐部。具体而言：北京、天津、内蒙古、辽宁、吉林、江苏、浙江、福建、江西、山东、河南、湖南、重庆、四川、云南等15省收敛于第一个俱乐部；河北、山西、黑龙江、广东、广西、海南、贵州、西藏、陕西、甘肃、青海、宁夏、新疆等13省收敛于第二个俱乐部；而上海、安徽、湖北等3省呈现发散趋势，不与其他任何地区收敛。数字化程度指数收敛的俱乐部虽不是完全符合我国东部、中部、西部的地理区划，但总体来看，数字化程度指数收敛的第一个俱乐部包含了东部地区和中部地区的绝大多数省份；而收敛的第二个俱乐部包含了西部地区的绝大多数省份，这说明在数字普惠金融的数字化程度方面，东部地区和中部地区的省份会收敛于相同的稳态水平，而西部地区的省份会收敛于相同的稳态水平。出现这种现象的可能原因是，北京大学数字金融研究中心课题组是从移动化、实惠化、信用化和便利化4个方面来编制数字化程度指标的，因此数字化程度主要与现代移动通信技术、地区商业化程度、地区市场化程度以及地区经济发展水平等息息相关，而这些因素均具有较强的溢出效应，东部地区和中部地区相互毗邻，这在一定程度上会促使中部地区向东部地区形成靠拢，最终收敛于相同的稳态水平。然而，西部地区由于深居内陆，与东部地区相距较远，而且中间还间隔了一个中部地区，因此受东部地区的辐射较小，因而很难跟东部地区收敛于同一个俱乐部。

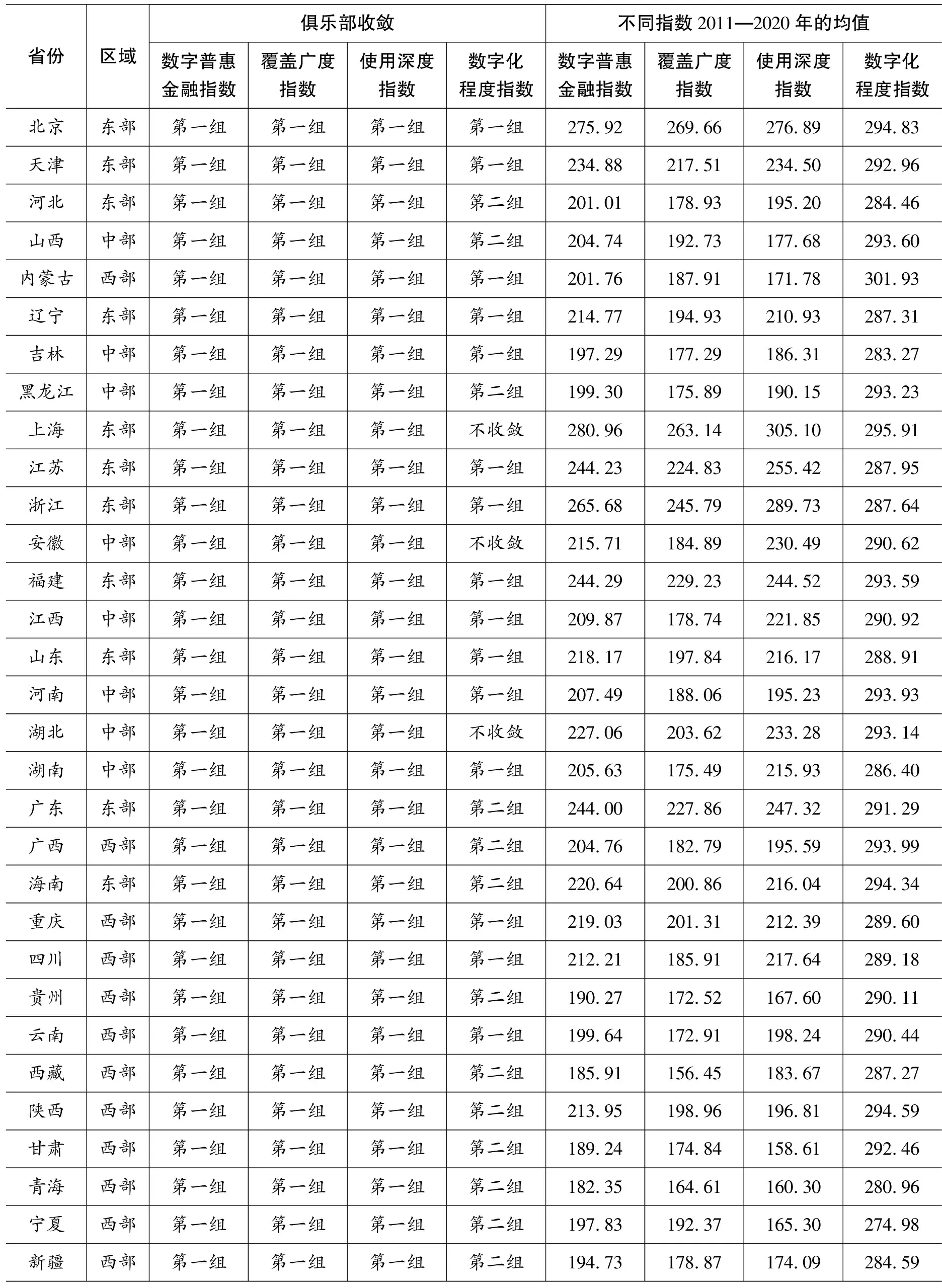
表3 数字普惠金融指数及其三个一级分指数的俱乐部收敛检验

五、研究结论与政策启示

为准确揭示中国数字普惠金融的现状及其动态演进特征，文章基于北京大学数字金融研究中心课题组发布的2011—2020年中国数字普惠金融指数，采用数理统计方法从时间和空间两个维度梳理了中国数字普惠金融的现状，并采用logt检验方法分别考察了中国数字普惠金融指数及其三个一级分指数的收敛情况。主要结论有：(1)在样本考察期间，我国数字普惠金融指数呈现出上升趋势，但存在较大的地区差异，呈现出东部、中部、西部依次递减趋势。(2)从分类指数来看，覆盖广度指数、使用深度指数和数字化程度指数均呈现出上升趋势，但覆盖广度指数和使用深度指数存在较大的地区差异性，而数字化程度指数在三大区域中相对均衡。(3)数字普惠金融指数、覆盖广度指数以及使用深度指数在全国范围内趋于收敛，而数字化程度指数总体不收敛，但存在俱乐部收敛，且东部地区和中部地区收敛于一个俱乐部，西部地区收敛于一个俱乐部。

基于本文的研究结论，我们可以得出以下启示：(1)在分析数字普惠金融的动态演进特征时，不能只看数字普惠金融指数的变化情况，还要看数字普惠金融不同维度分指数的变化情况，只有这样才能准确掌握数字普惠金融的动态演进特征。(2)尽管数字普惠金融指数在全国范围内趋于收敛，但其三个一级分指数并不是全部收敛的，其中，数字化程度指数总体不收敛，且使用深度指数呈现发散趋势，因此提高落后地区数字普惠金融的使用深度和数字化程度显得迫在眉睫，而且这是实现数字普惠金融均衡发展的重要措施。(3)覆盖广度指数在全国范围内趋于收敛，这提醒我们当用户规模达到一定级别以后，数字普惠金融指数的增长点只可能来自使用深度和数字化程度，因此使用深度与数字化程度是数字普惠金融未来拓展的重要方向。