基于PFC2D隧洞注浆混凝土三点弯曲梁破坏模拟
2022-02-17田林昌季日臣
田林昌, 季日臣
(1.兰州交通大学土木工程学院, 兰州 730070; 2.兰州交通大学土木工程学院, 兰州 730070)
Cundal[1]在1971年提出了离散单元法,其方法适用于在准静力条件下或动力条件下的节理系统或块体集合的问题,最初用于研究岩土边坡的问题。
颗粒流计算程序(particle flow code,PFC)是基于离散元模型的分析程序。国内学者利用离散元方法,结合工程实际案例,取得了很多研究成果。尹阳阳等[2]发现试件自身重量对混凝土断裂性能有极大影响,研究发现混凝土三点弯曲梁尺寸和起始缝高比两者较大时需考虑自重引起的CMODini(裂隙口张开距离)的影响。丁永政等[3]研究三点弯曲梁在外荷载作用下的破坏模式,用颗粒流程序PFC2D对存在不同位置和高度的预置裂隙的三点弯曲梁受压破裂过程进行了模拟,研究表明试件在含不同高度预置裂隙下破坏模式和破坏机制有较大差别。王思莹等[4]根据离散元思想,采用混凝土刚体弹簧模型,研究了混凝土楔入劈拉试验和三点弯曲切口梁的断裂过程。刘妙燕等[5]通过橡胶混凝土三点弯曲梁断裂试验,得到了混凝土的荷载、挠度和裂缝开口位移值,认为掺入橡胶后混凝土韧性和变形能力提高,脆性得到了改善,并可利用经验式推断达到某一声发射能量值时混凝土的破坏程度。刘超[6]应用真实破裂过程分析(realistic failure process analysis,RFPA)程序对完好岩石试件以及含有单个裂纹和交叉裂纹的岩石试件在单轴压缩下的破坏过程进行数值模拟模拟。结果表明完好岩石试件和含有不同裂隙岩石试件破裂过程发展规律的不一致性。胡少伟等[7]为探究不同尺寸混凝土三点弯曲梁试件断裂过程的不一致性及其尺寸效应,分别取高度为0.25、0.30、0.40、0.50 m的4组16根不同尺寸试件,对其进行断裂试验,分析了起裂和失稳荷载、荷载张口位移曲线的变化。管俊峰等[8]认为在裂缝黏聚力作用下,通过Paris位移公式得出混凝土三点弯曲梁裂纹发展过程中断裂过程区上的裂缝延伸位移的解析表达式,结果表明其方法简单且有效。石明宇等[9]研究了隧洞运行期间衬砌混凝土受低温度场影响,并进行数值模拟试验,结果表明,不同温度工况下对混凝土强度与稳定性有较大影响。李守巨等[10]通过PFC2D巴西劈裂试验,以细观参数为基础,得出以估计的细观参数,通过试验模拟与实际试验吻合度较高,较好地验证了其本构关系,吴胜智等[11]利用FLAC3D和PFC3D耦合程序,研究认为隧洞豆砾石在注浆前,其单位填充体积,颗粒的迁移都会对地层沉降产生影响。而对上部岩体的沉降对注浆之后的混凝土的受压破坏尚未深入研究,因此,有必要利用PFC2D离散元程序模拟研究隧洞上部岩体对豆砾石回填灌浆层混凝土的受压破坏机理。
通过PFC2D颗粒流离散元程序,建立二维隧洞模型,检测开挖过程中的隧洞上部沉降,对因隧洞上部沉降而引起的隧洞豆砾石回填灌浆层混凝土受压破坏进行数值模拟,根据实际工程和数值计算确定的细观参数建立回填灌浆层数值模型,通过PFC2D颗粒流程序,利用平行黏结模型来模拟颗粒与骨料间的接触模型,最终生成三点弯曲梁模型。以往数值模拟试验大多建立在以连续介质模型的基础之上,如利用FLAC3D或FLAC2D等程序,其存在的最大短板是无法从微观角度观察混凝土等材料在受压或受拉状态下的细观变化。以二维为基础的目的则是为了更加直观地观察混凝土试件在受压或受拉过程裂纹的发展。基于此,现依托甘肃省白龙江深埋长输水隧洞工程提供的回填灌浆层粗、细骨料的宏观参数进行细观参数标定,通过模拟,综合分析不同加载速度、不同平行黏结模量下,试件的损伤和断裂过程[12],以期得出回填灌浆层混凝土弯曲梁的受压破坏规律,对实际工程设计、施工、运行具有重要的参考价值。
1 颗粒流离散元软件原理
数值试验利用基于颗粒流模拟理论的离散元PFC2D程序实现。为更好地实现回填灌浆材料的各方面力学性能和模拟的效果,隧洞模型颗粒间的接触本构模型使用线性抗转动模型。模拟回填灌浆层混凝土的接触本构模型使用平行黏结模型。
平行黏结模型提供了在两个接触片之间沉积的有限尺寸的类水泥材料的力学行为。平行黏结组件与线性组件平行作用,并在片之间建立弹性相互作用。平行键的存在并不排除滑移的可能性。平行键可以传递各块之间的力和力矩,可以想像为一组具有恒定的法向刚度和剪切刚度、均匀的弹性弹簧。
平行黏结模型的接触力Fc和接触力力矩Mc为
(1)

(2)

将平行黏结力分解为法向力和剪切力,将平行黏结力矩分解为扭转力矩和弯矩:
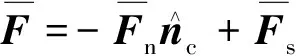
(3)
(4)
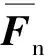
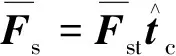
(5)
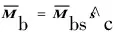
(6)
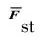


(7)
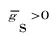
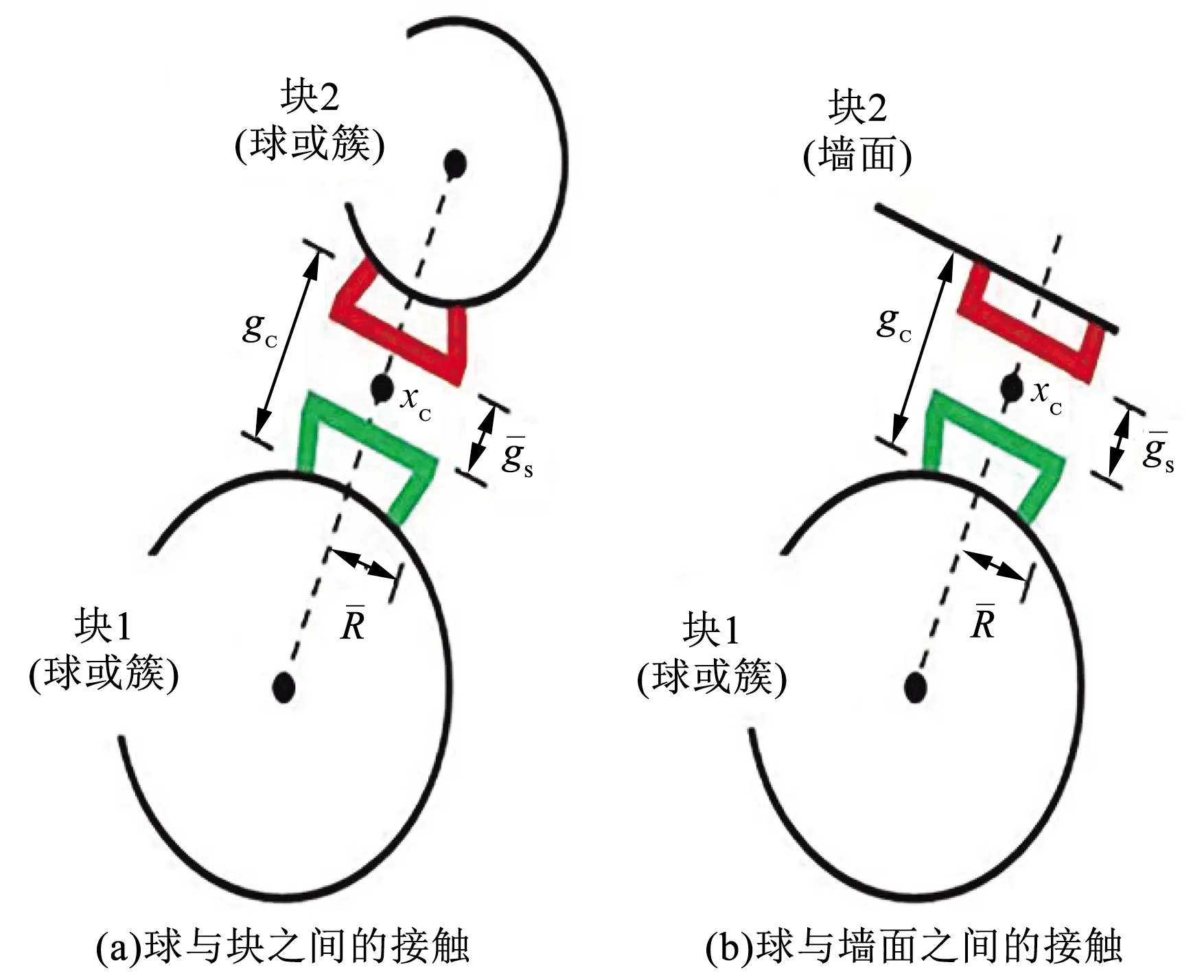
gc为球与簇或球与墙面之间的距离;为接触面半径;xc为两个 接触中心线的中点图1 两种基本接触类型Fig.1 Two basic contact types
2 数值模拟方案设计
2.1 回填灌浆层三点弯曲梁建模
(1)生成颗粒。使用PFC2D中的ball来模拟回填灌浆层中的细骨料,生成球颗粒,模拟豆砾石颗粒利用计算机辅助设计程序(computer aided design,CAD)画结构图导入dxf文件来生成。
(2)预压。胶结材料一般在一定的压力下生成,回填灌浆层亦不例外,与岩石的高应力下的形成条件不同,回填灌浆层生成于岩层与预制衬砌之间,为防止在程序中生成颗粒后重叠量过大,需要在颗粒流程序模拟给予其预压值,但值不需要太大。
(3)加胶结。模拟对象为类似于混凝土的回填灌浆材料,应用离散元平行黏结模型,模拟细骨料与粗骨料的结合。
(4)卸载。以实际工程为研究对象,给定一个围压值,模拟取样过程。
(5)加载。给加载墙体一个竖向的速度,加载时给加载棒摩擦系数,使得给试样的力是向下的。不会由于颗粒的离散性导致出现横向移动。
2.2 离散元模型的细观参数
平行黏结模型由7个参数定义,平行黏结模量、平行黏结法向刚度、切向黏结刚度、法向强黏结度、切向黏结强度、摩擦角以及摩擦系数。具体细观参数如表1和表2所示。
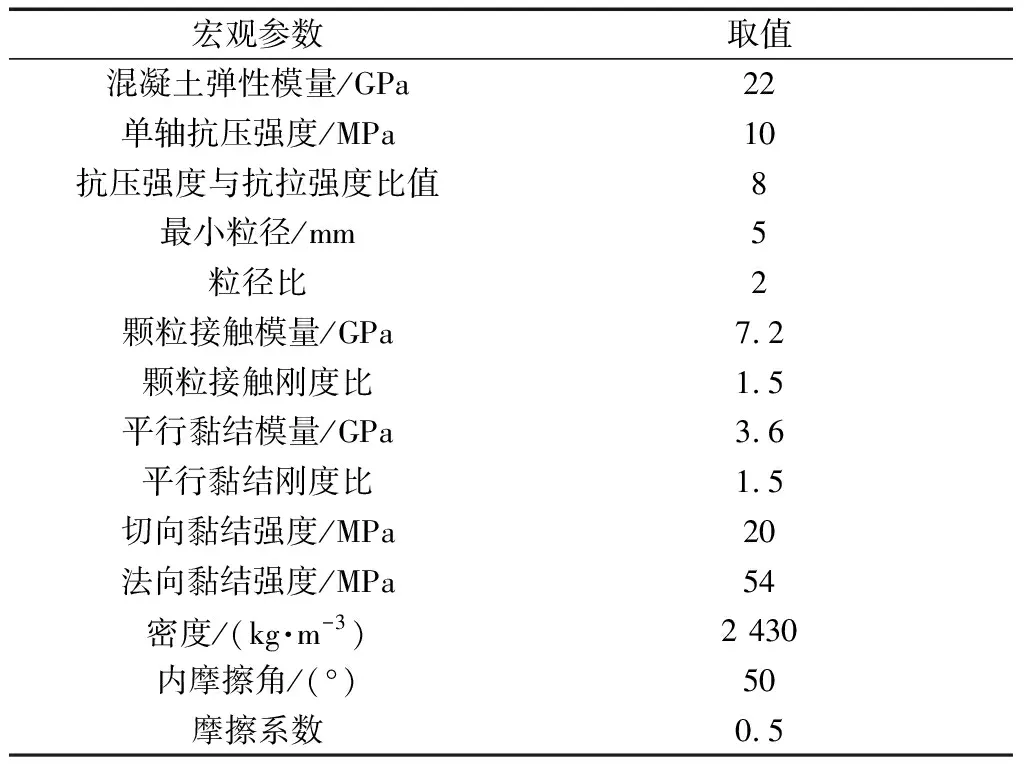
表1 回填灌浆层三点弯曲梁模型参数Table 1 Parameters of three-point curved beam model in backfill grouting layer
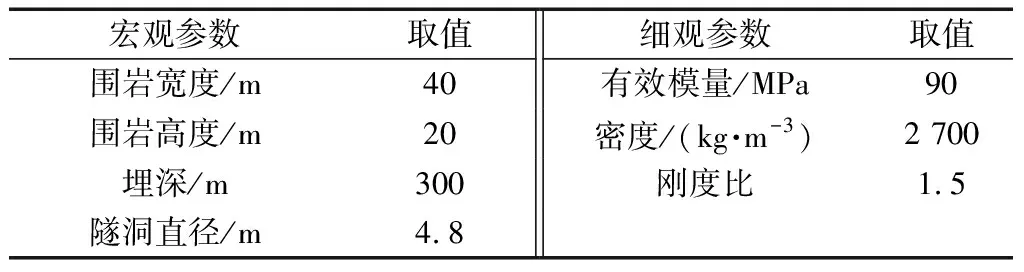
表2 隧洞模型参数Table 2 Parameters of tunnel model
离散元模型高400 mm、宽1 000 mm,边界采用墙(wall)来模拟,生成细骨料和豆砾石后,删除边界墙,并同时生成上部圆形加载墙,给上部圆形wall速度,下部两个圆形墙体不施加任何速度,模拟实际工程中固定的衬砌,利用PFC2D中的簇clump模拟豆砾石,clump数量为2 800,粒最小粒径5 mm,最大与最小颗粒粒径比为2,颗粒数量为4 585,利用PFC2D内置的fish函数,颗粒将会在最小与最大粒径之间随机生成,然后通过粒径扩大法来调整模型内的颗粒分布,通过内置fish语言,利用墙体伺服机制控制模型在试验过程中的预压,围压,再通过设置加载墙在试件上部中心处给予一个速度,对其加载。
隧洞模型宏观及细观参数如表2所示。
上部圆形墙体的加载速率V=应变率×wly,其中,应变率是时间的倒数,wly为模型上部与下部位置变化量的差值。
研究方案设计如下。
(1)通过布置测量点,模拟仿真隧洞沉降,得到隧道沉降曲线。由于隧洞上部沉降的存在,对回填灌浆层混凝土受压破坏进行分析。通过受压破坏下裂纹的发展,分析应力、力链。
(2)针对回填灌浆层混凝土,改变平行黏结模量,研究在同一加载速度下不同平行黏结模量对胶结破坏能的影响。
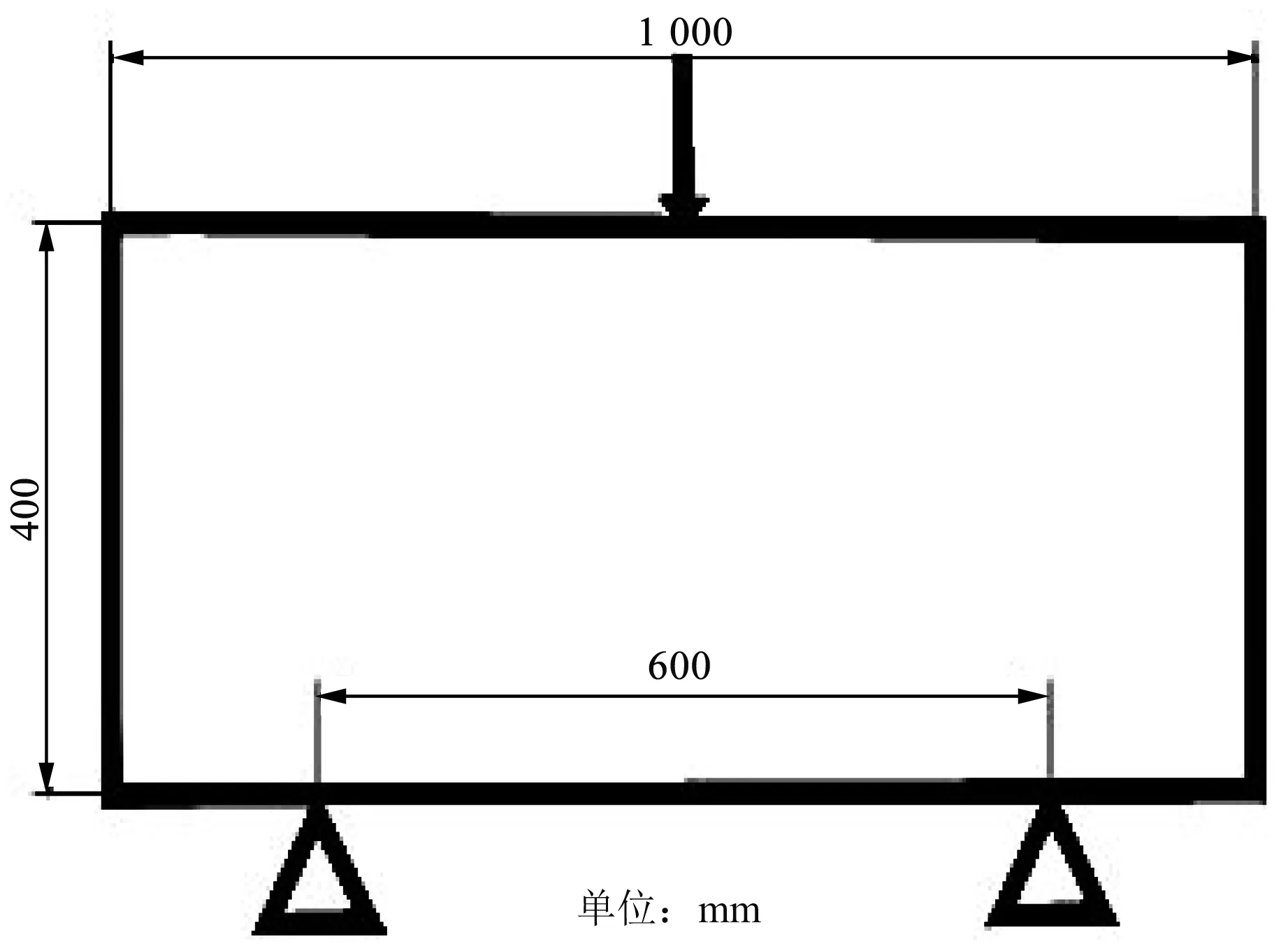
图2 受力结构图Fig.2 Force structure diagram
(3)检测同一加载速度、同一平行黏结模量下的内部颗粒位移变化情况,从微观角度研究颗粒在同一破坏模式下的破坏机制。
3 结果分析
3.1 隧洞沉降分析
隧洞沉降矢量图和沉降拟合曲线,如图3~图5所示,两者表明,上部沉降较大,根据拟合曲线得知,最大沉降量3.6 cm。实际工程中输水隧洞回填灌浆层混凝土正是由于上部岩体的沉降而发生破坏,回填灌浆层混凝土的存在目的是为了抵抗围岩沉降、将沉降所施加的力均匀传递,直至减小至对衬砌几乎不受影响。
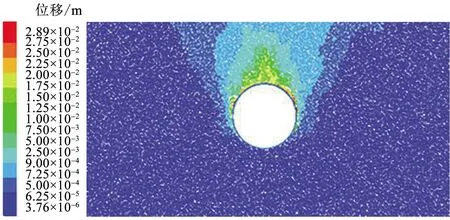
图3 隧洞开挖后位移场Fig.3 Displacement field after tunnel excavation

图4 隧洞沉降矢量图Fig.4 Vector diagram of tunnel settlement
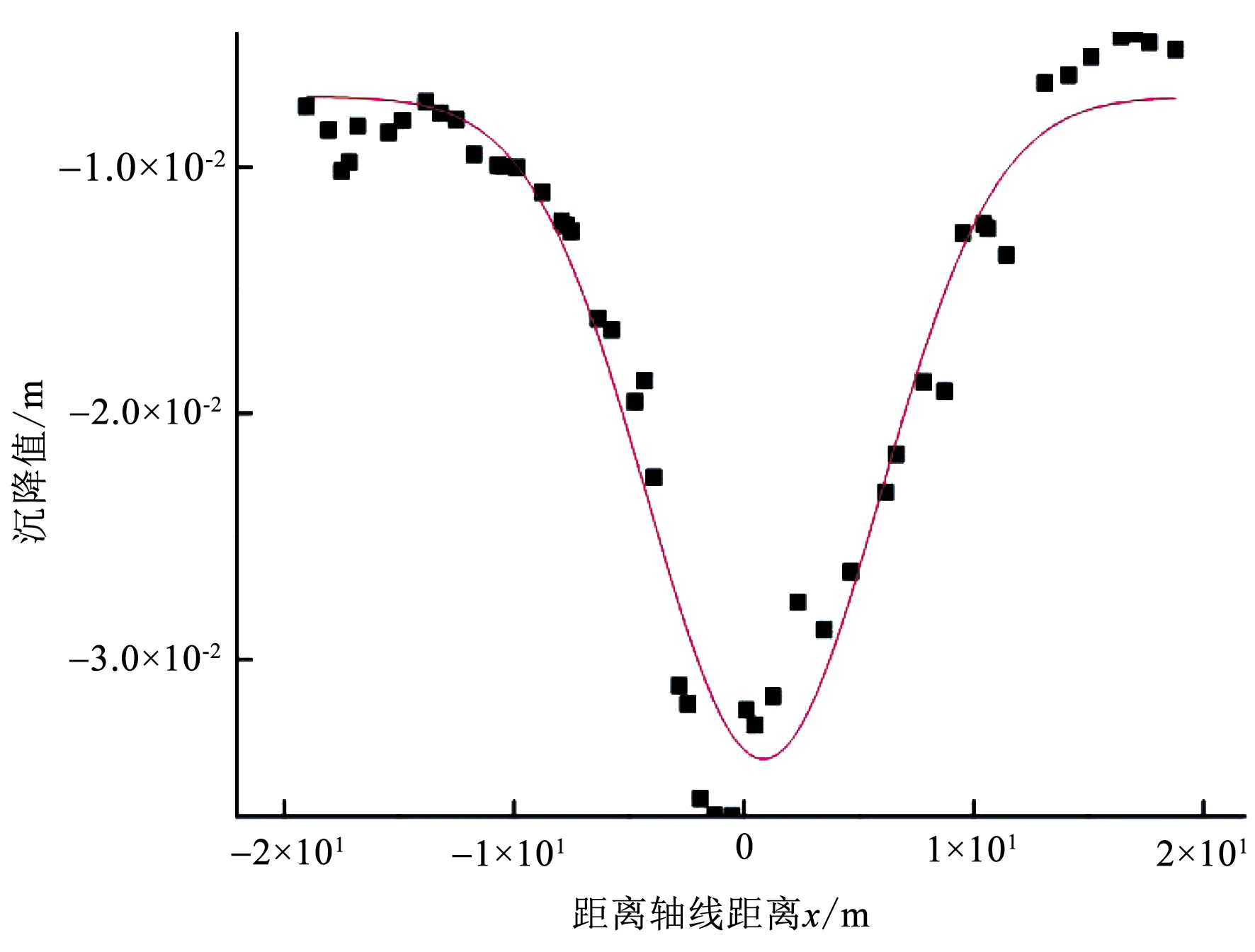
图5 沉降值拟合曲线Fig.5 Fitting curve of settlement value
3.2 回填灌浆层混凝土破坏分析
3.2.1 应力分析
根据力-位移法则,基于平行黏结接触模型,试件在上部受压过程中,颗粒与颗粒间存在法向和切向平行黏结力,当试件受力超过材料的极限抗拉强度,试件会在受拉中破坏黏结,产生法向平行黏结应力。
法向平行黏结力为
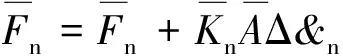
(8)
平行黏结弯矩为
(9)
Mb=Kbθb
(10)
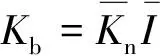
(11)
得到法向平行黏结应力为
(12)
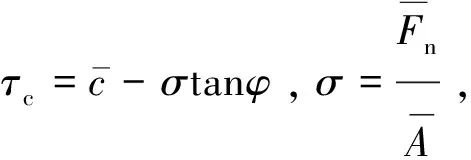
切向平行黏结力为
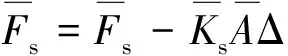
(13)
于是得到切向平行黏结应力为
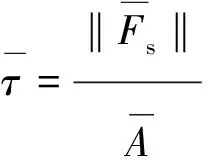
(14)
图6给出了试件在未开裂时的x方向应力σx、y方向应力σy、剪应力τxy应力云图。上部圆形加载墙处受压,由于底部支撑的作用,圆形加载墙正下方受拉,如图6(a)所示,y方向在加载处及下部支持点处受压,其余位置均表现为受拉。切应力云图说明在加载处正下方位置受剪应力为负值,左右两边右侧剪应力为正值,左侧剪应力为负值,表明左右两侧受剪切的方向都指向裂纹发展的位置。
当试件出现裂纹后(图7),σx云图上部加载处受压迅速减小,加载处正下部受拉也迅速减小,受拉部分主要集中在裂纹位置。σy云图中由于裂纹发展导致试件原来受拉区域发生改变,未开裂时的受拉区域,在开裂后转变为受压状态,同时底部两个支撑处受压减小,剪应力的发展与未开裂时基本一致(图8),受剪方向都指向裂纹出现位置。

图6 未开裂应力云图Fig.6 Uncracked stress nephogram
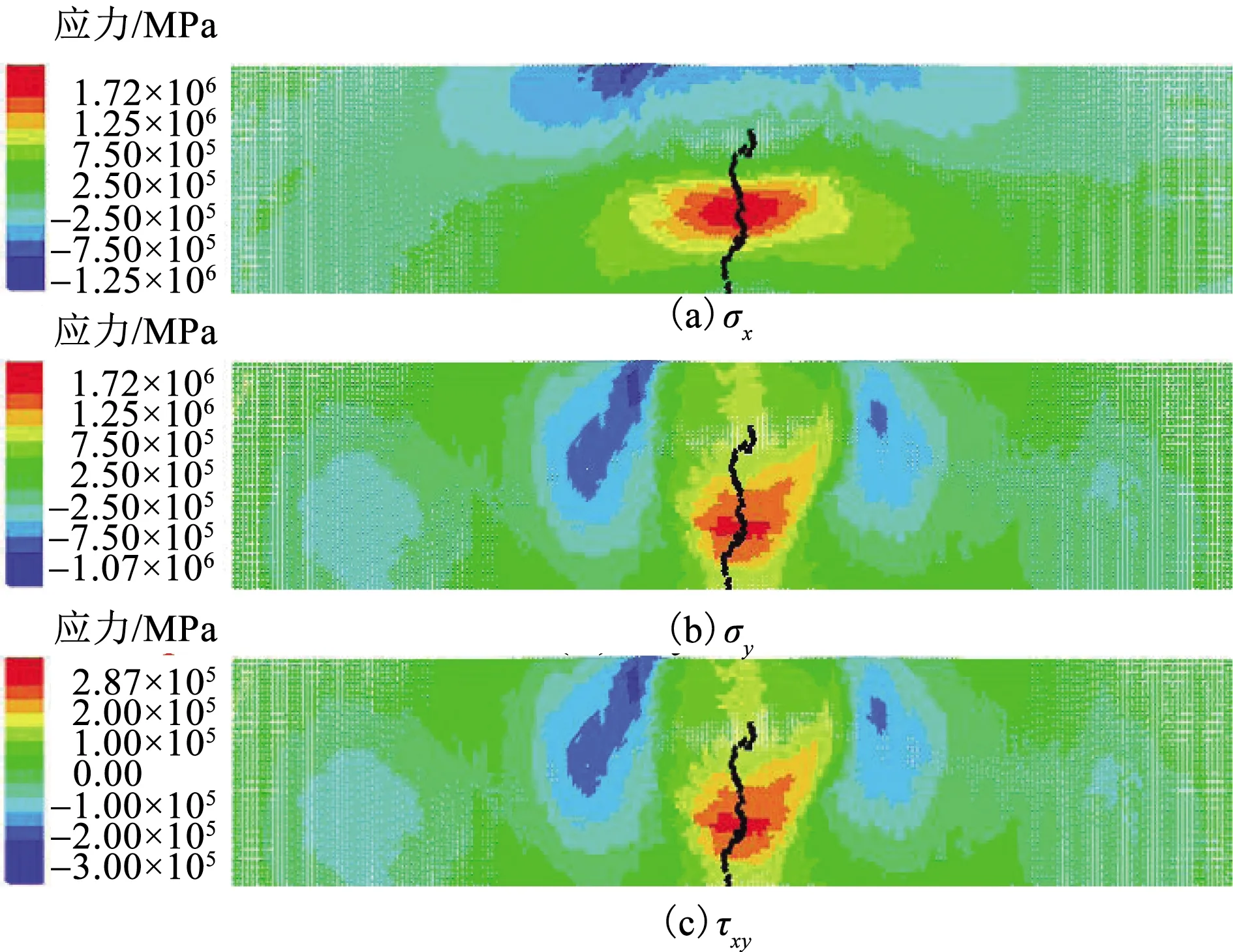
图7 开裂后的应力云图Fig.7 Stress nephogram after cracking
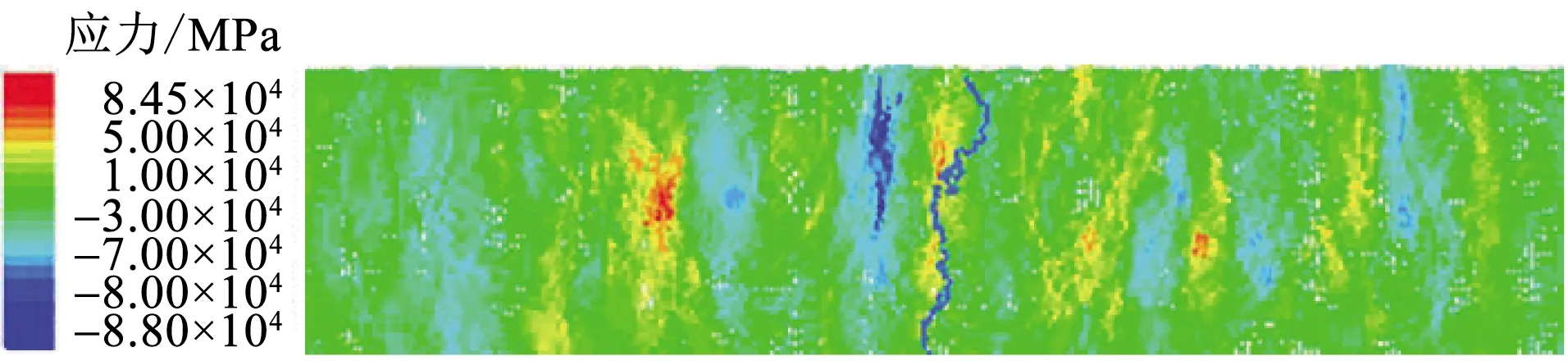
图8 裂纹贯穿后的τxy应力云图Fig.8 Stress cloud after crack penetration
裂纹贯穿后,试件内部应力减小,受拉应力和压应力区域散乱分布,未呈现规律性。
3.2.2 加载速度敏感性分析
试件在加载时给予不同加载速度时,其破坏模式有较大差别。在PFC2D中,加载速率是一个较为重要的参数。对于加载速率的选取,Zhang等[13]已经做出了详细的分析,认为准静态加载速率上限为0.08 m/s。选取了0.02、0.002、0.000 2 m/s三种加载速度来研究加载速度对破坏模式的改变。在加载速度0.000 2 m/s时,试件未出现裂纹(图9),说明加载速度过小,无法导致试件破坏。
在两种不同加载速度之下,剪切裂纹数量要远远多于拉伸裂纹数量,但拉伸裂纹出现的时间要略早于剪切裂纹出现的时间。这表明,当上部施压时,底部最先出现的是拉伸裂纹,随后立即出现剪切裂纹,随着不断加载,较大的加载速度之下的拉伸裂纹将不再发展,剪切裂纹成为主要裂纹,而在较小的加载速度下,拉伸裂纹会继续发展,但数量增长缓慢,数量也较少,剪切裂纹则迅速增多,直至试件完全破坏。
综合分析应力云图和不同加载速度下的裂纹类型及数量,结果表明:试件破坏最初是由于底部受拉应力作用,而当开始出现裂纹后,试件继续加载,受拉区域随裂纹发展而改变,裂纹类型也发生了
改变,剪切裂纹迅速增多。裂纹贯穿后,应力迅速减小,试件内部呈现应力均匀分布。
3.3 力链分析
颗粒体表现的动态受力特性和静态堆积性质与细观尺度力链的衍变规律存在极大的相关性。根据孙其诚等[14]的研究,颗粒间的摩擦系数是影响力链的最主要的宏观参数。以颗粒摩擦系数0.5为研究对象,粒径为2~4 mm的细骨料颗粒和粒径为5~10 mm的豆砾石颗粒,重力加速度9.8 m/s2。从力链角度揭示颗粒的静态和动态性质。
图10(a)为试件初次出现裂纹时的接触力分布,上部加载处和底部支撑处表现为强力链,即为图中深蓝色较粗部分,该部分力链主要是模拟豆砾石颗粒产生的。其余部分表现为弱力链。当裂纹以较快速度增长时,如图10(b)所示,强、弱力链基本呈均匀分布,颗粒间接触力的大小开始减小。当外荷载不断增大时,如图10(c)所示,强、弱力链的方向与加载力的方向大体一致。裂纹贯穿后上部荷载继续加载,强、弱力链的值继续减小。
3.4 胶结破坏能分析
试件在出现裂纹后,存在能量的产生与消耗,胶结破坏能就是其中之一[15],为了探究胶结破坏能的产生与那些因素有相关性,选取了两个对胶结破坏能的产生可能存在较大影响的变量,加载速度和平行黏结模量。
裂纹产生的时间的早晚,受加载速度的影响,由之前的模拟所得到的结论,初始加载速度为0.002 m/s,裂纹出现的时间为200 000步,当加载速度增大时,裂纹出现时间提前,图11给出了当给加载墙不同加载速度,胶结破坏能产生的时间和大小,当加载速度增大,胶结破坏能产生的时间提前,但所产生的能量三者之间几乎相同。加载速度对胶结破坏能的影响体现在其产生的时间的早晚,对最终能量的大小影响较小。
图12给出了在相同加载速度下,平行黏结模量取不同值对胶结破坏能的影响,以黏结模量3.6 GPa为基本对比数据,当黏结模量增大,胶结破坏能出现时间提前,但所产生的能量是最少的,与之相反,当黏结模量增大,胶结破坏能出现时间最晚,但产生了最多的能量。说明当黏结模量增大,试件不易被破坏,颗粒黏结更加稳固。
由于上部加载墙的不断加载,造试件内部能量积累,当能量积累达到某一临界值,裂纹开始萌生,累积的能量以胶结破坏能的形式被释放。裂纹萌生并快速发展的根本原因能量的积累和发散,其促进了裂纹的出现和扩张,结果是造成试件贯穿破坏。
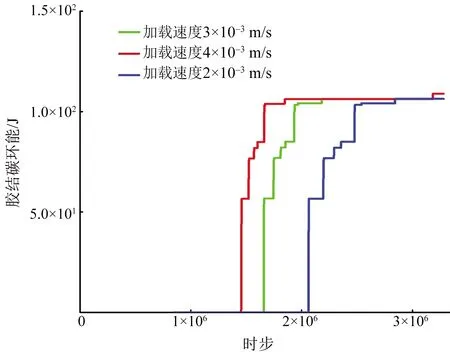
图11 不同加载速度下的胶接破坏能Fig.11 Bonding failure energies at different loading rates

图12 不同黏结模量下的胶结破坏能Fig.12 Cement failure energies under different bond moduli
3.5 位移场分析
试件内部裂纹产生和发展的动态过程需要从更加精细的角度去研究,并且从试件整个裂纹发展的动态过程来研究,从微观角度出发分析。以加载速度0.002 m/s时的位移云图为例对试样内部颗粒进行监测。图12给出了在试样的初期阶段,位移首先出现在上部圆形加载墙正下方部位,如图13(a)所示,沿着加载墙向试样的下部慢慢扩散,随着上部圆形墙体不断的施加力,圆形加载墙正下方的颗粒位移有增大的趋势,模拟豆砾石颗粒的位移在试件上部和下部位的方向相反,且大小不同,同时加载墙两侧位移值逐渐变大,且位移基本上呈对称分布,由中间至两侧位移呈带状分布,如图13(b)~图13(f)所示。试件破坏后,如图13(g)所示,裂纹的产生使局部位移发生改变,中部颗粒位移增大,两侧位移值不断减小,随着裂纹的扩张至整个试件被贯穿,颗粒趋于稳定。
整个模拟过程细骨料颗粒的位移基本保持不变,而模拟豆砾石颗粒位移产生少量变化,符合实际工程中细骨料材料由于回填灌浆材料的胶结而无法发生错动,偏移,而回填灌浆层中豆砾石在上部围岩压力的作用下由于裂纹的发展而产生局部的位移变化。试件在裂纹部位位移显著超过其他位置,说明试件在裂纹部位有剥落的迹象。
4 结论
通过颗粒流程序,模拟隧洞沉降,分析由于隧洞沉降引起的回填灌浆层混凝土破坏。主要结论叙述如下。
(1)输水隧洞在开挖完成后需要立即对衬砌外层吹填豆砾石并灌浆以抵抗上部围岩沉降。通过建立PFC2D二维隧洞模型,得到沉降值约3.6 cm。
(2)分析回填灌浆层混凝土三点弯曲梁破坏,结果表明,试件内部应力状态在试件裂纹出现之前和出现之后被改变。裂纹贯穿之后试件内部应力未完全消失,但呈现均匀分布。加载速度敏感性分析表明,加载之初,试件最先出现拉伸裂纹,之后快速出现剪切裂纹。在不同加载速度下,剪切裂纹数量多于拉伸裂纹数量,加载速度增大,裂纹出现的时间提前。
(3)摩擦系数对接触力的影响通过细观尺度力链分布来反映,强、弱力链分布反映接触力的大小,力链的方向与加载力方向基本一致,接触力与重力方向是否一致以及两者之间存在的夹角大小范围,该部分内容有待继续研究。
(4)在试件破坏过程中,在加载之初开始有能量的累积,当能量不断累积到某一临界值时,试件不间断施加力,试件开始破裂。影响胶结破坏能的主要因素是平行黏结模量,加载速度对破坏能的影响从根本上分析是破坏发生的早晚。
