基于天牛须搜索算法的短期风电功率组合预测

单斌斌， 李华*， 谷瑞政， 李玲玲

(1.河北工业大学电气工程学院/省部共建电工装备可靠性与智能化国家重点实验室/河北省电磁场与 电器可靠性重点实验室， 天津 300130； 2.国网天津市电力公司检修公司，天津 300232)

风电作为一种可再生的清洁能源，其技术相对成熟，是目前应用最为广泛的新能源发电方式之一[1]。但风电场输出功率的不确定性是风电面临的一系列并网问题的根源之一，对风电场输出功率进行准确预测是降低风电输出功率不确定性的最有效手段。经过多年发展，功率预测已成为风电调度运行技术的主要组成部分，为大规模风电的有效消纳提供了重要支撑。因此研究风电功率预测具有重大意义[2]。

目前，风电功率预测模型分为物理模型和统计模型。搭建物理模型不需要历史数据，但需要结合风电场的具体环境，方法复杂度太高。统计模型只需要风电场的历史测量数据来搭建学习模型，最常用的统计学习模型包括时间序列分析模型[3]，神经网络模型和支持向量机模型等[4]。文献[5]采用时间序列法和BP(back propagation)神经网络对同一风电场进行了短期功率预测。文献[6]采用极限学习机(extreme learning machine, ELM)对风电场进行了超短期风电功率预测，并与BP神经网络进行对比分析。结果表明极限学习机收敛速度更快，预测精度更高。

由于单一预测模型具有局限性，为了减少风电功率的波动性，提高预测精度，将原始风电功率序列使用信号分解技术进行分解[7]。文献[8]采用小波分析分解风电功率序列，预测精度得到显著提高。但是小波基选取难度较大，缺乏自适应性，而经验模态分解依据数据自身的时间尺度来进行信号分解，无需设定任何基函数，泛化性能更好。文献[9]提出了改进经验模态分解和支持向量回归的模型，提高了预测精度，但模态混叠的问题得不到解决。文献[10]采用基于完全集成经验模态分解(complete ensemble empirical mode decomposition adaptive noise, CEEMDAN)和支持向量回归的预测模型，不仅解决了模态混叠问题，还消除了残留噪声，但模型参数初值依旧存在选取困难的问题。

近年来一些新的智能优化算法在机器学习参数优化中脱颖而出。文献[11]采用花朵授粉算法优化BP神经网络的参数，降低了预测误差。但算法收敛速度慢，且容易陷入局部最优。文献[12]提出了一种改进天牛须搜索算法(improved beetle antennae search, IBAS)优化最小二乘支持向量机的短期电力负荷预测模型。算例结果表明，该模型运算时间短，且算法稳定性高。

因此，现提出一种完全集成经验模态分解、极限学习机和改进天牛须搜索算法相结合的风电功率预测模型。利用CEEMDAN将原始风电功率历史数据分解为简单序列分量，对各序列分量分别用IBAS-ELM模型进行预测，将各分量的预测值进行叠加得到最终预测值，以期获得精确度更高的风电功率预测值。

1 完全集成经验模态分解

经验模态分解(empirical mode decomposition, EMD)假设任何原始信号都是由不同震荡模式组成的，原始信号经过EMD分解后，会得到一组按照频率和振幅大小排列的本征模函数(intrinsic mode function, IMF)。EMD[13]将原始信号v(t)分解为

(1)

式(1)中：v(t)为原始信号；k为IMF分量的总数；imfj为第j个IMF分量；r(t)为残余分量。

由于EMD算法在分解信号时容易出现模态混叠现象，为了改进这个问题，提出了集合经验模态分解法(ensemble empirical mode decomposition, EEMD)，EEMD算法是在EMD的基础上添加一组服从正态分布的高斯白噪声，有效避免了EMD分解出现的模态混叠现象。但添加白噪声使EEMD运算量变得很大，并且添加的白噪声集总平均之后不能完全抵消，会存在残留，导致重建之后残留噪声造成的误差不可忽略。为了解决这个问题，互补集合经验模态(complementary ensemble empirical mode decomposition, CEEMD)被提出，与EEMD不同的是，CEEMD是将原始信号加上白噪声与原信号减去白噪声分别进行EMD分解，求两者均值，用于抵消加入的噪声。该方法不仅节省了计算时间，还消除了残留噪声，但如果参数选择不当，会产生错误成分，导致得到的IMF不符合IMF定义。

针对上述分解算法存在的问题，采用添加自适应白噪声的CEEMDAN来对原始信号进行分解，CEEMDAN通过在各个分解阶段添加自适应白噪声，不仅可以消除模态混叠，还能使信号重建后完整且无噪音。与CMMED相比，CEEMDAN的运算量更小，分解速度更快。

2 改进天牛须搜索算法

2.1 天牛须搜索算法

天牛须搜索算法(beetle antennae search, BAS)是一种模仿天牛觅食的智能优化算法[14]。天牛有两只长触角，如果右侧触角收到的气味强度大于左侧，那么天牛会在下一步往右飞，否则就往左飞。根据这一简单原理天牛就可以有效找到最优解。由于BAS只需要一只天牛，所以运算量非常小，收敛速度非常快。BAS的具体实现步骤如下。

(1)确定搜索空间维度为n，天牛质心为x，天牛左须为xl，天牛右须为xr，两须间距离为d，其中x、xl、xr都是n维向量。

(2)初始化天牛位置，由于天牛头朝向随机，所以随机生成n维单位向量a来表示天牛头朝向，即

(2)

式(2)中：rands(n,1)为生成n维向量。

(3)确定天牛左右须的空间位置。

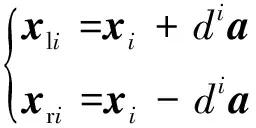
(3)

式(3)中：i为迭代次数；xli、xri分别为天牛左须与右须在第i次迭代中的空间位置；di为在第i次迭代中天牛两须之间的距离。

(4)计算两须适应度值以及确定步长因子。

(4)

式(4)中：fl、fr分别为左右两须的适应度值；δi为第i次迭代时天牛的移动步长。

(5)天牛更新位置。

xi=xi-1+δiasign(fl-fr)

(5)

式(5)中：sign()为符号函数。

(6)更新两须间距离。

di=0.95di-1

(6)

(7)判断是否符合迭代结束条件，符合则结束，不符合则重复步骤(2)～步骤(6)，直至符合结束条件。

2.2 天牛须搜索算法改进策略

天牛须搜索算法具有良好的全局搜索能力，但局部搜索能力有待提高。给天牛须搜索算法增加一个动态惯性权重来增强天牛的局部搜索能力，动态惯性权重是一种能够协调搜索能力的有效机制，能够动态平衡优化算法的全局搜索能力和局部搜索能力，从而使天牛在搜索过程中可以顺利找到最优解。权重w的取值方法为

(7)

式(7)中：wmax=0.9；wmin=0.4；imax为最大迭代次数。

在天牛的位置更新公式中引入动态惯性权重w对天牛的位置更新方式进行优化，使天牛在自我学习时可以按照惯性策略进行调整，改进天牛须搜索算法的位置更新公式为

xi=wxi-1+δiasign(fl-fr)

(8)

3 模型组合

3.1 极限学习机

ELM随机生成权值和阈值，并且在训练过程中无需进行调整，仅需设置隐藏层神经元的数量，就可以求出最优解。ELM的数学模型为

Hβ=Q

(9)

式(9)中：H为网络隐藏层的输出矩阵；β为权值矩阵；Q为目标期望输出矩阵。

ELM的训练目标是要找到模型的最优权值组合W=(w,b,β)，使式(10)成立：

minE(W)=min‖Hβ-Q‖

(10)

式中：w为隐藏层节点的输入权值；b为隐藏层的偏置。在ELM算法中，输入w和b，输出矩阵H就会被唯一确定。此时，ELM的训练过程即求解式(9)的线性方程组，其最优解为

(11)

式(11)中：H+为隐藏层输出矩阵H的Moore-Penrose广义逆。

3.2 IBAS优化ELM的基本原理

由于ELM的权值和阈值是随机生成的，训练精度和时间都会受到随机性的影响。采用IBAS算法对ELM的权值和阈值进行优化，将得到的权值和阈值用于ELM的训练，得到最终的ELM网络结构。IBAS-ELM预测模型的步骤如下。

(1)初始化ELM，设置输入层、隐藏层和输出层的节点数，初始化网络权值和阈值。

(2)设置IBAS算法的参数，初始化天牛的位置。

(3)将ELM的初始权值和阈值编码到天牛中，并确定IBAS算法适应度函数，选取使适应度函数最小的权值和阈值。选择的适应度函数为

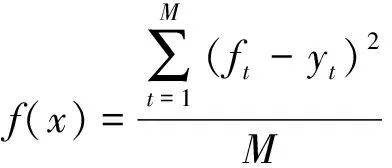
(12)

式(12)中：ft为测试样本中第t个样本的实际值；yt为测试样本中第t个样本的模型预测值；M为对应的样本数。

(4)由式(4)来计算天牛左右须的适应度函数fl和fr。

(5)天牛根据式(8)来进行位置更新，并保留适应度值最小的天牛位置。

(6)判断是否满足IBAS算法的结束条件，若满足转步骤(7)；若不满足，转步骤(4)。

(7)将最优值的天牛进行解码，生成的最优解作为ELM的初始权值和初始阈值进行训练。

综上所述，给出IBAS优化ELM参数的具体流程图，如图1所示。

3.3 CEEMDAN-IBAS-ELM预测模型

构建的短期风电功率预测模型，具体实现步骤如下。

Taking the AC actuator load and the DC motor load as examples, the correctness and validity of the model in normal mode and fault mode are respectively verified.

(1)使用CEEMDAN将原始风电功率序列分解为9个IMF分量和1个RSE分量。

(2)将分解后的各个IMF分量和RES分量分别作为预测模型的输入量，采用IBAS算法优化ELM的权值和阈值，得到各分量优化后的预测模型。

(3)将分解后的各个IMF分量和RES分量送入训练好的各分量的ELM模型进行预测，得到各分量的预测值。

(4)叠加每个分量的预测值来获得风电功率的最终预测值。

(5)对获得的风电功率预测值和风电功率实际值进行误差分析。

基于CEEMDAN-IBAS-ELM预测模型的示意图，如图2所示。

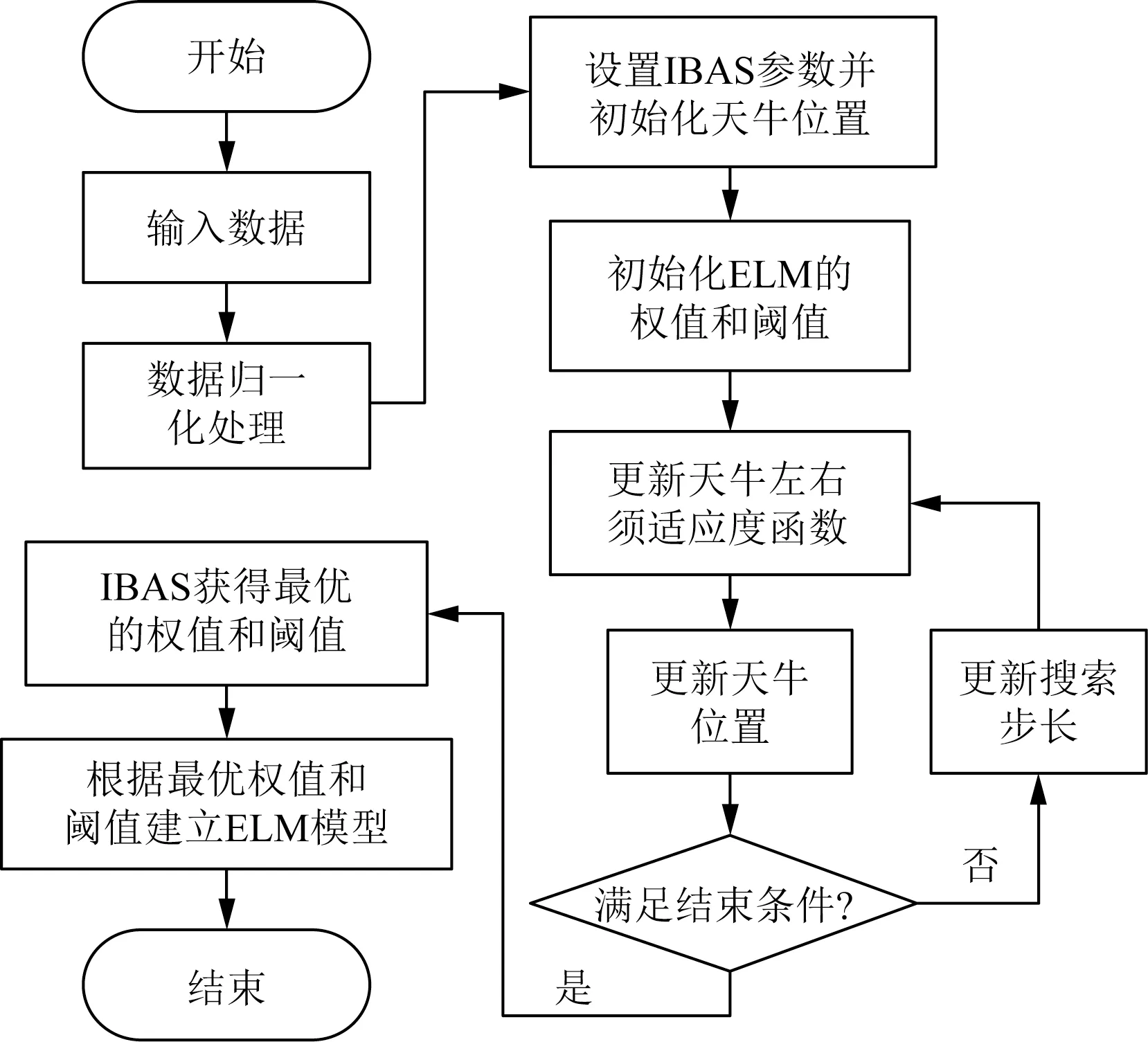
图1 IBAS优化ELM参数流程图Fig.1 IBAS optimization ELM parameter flow chart

图2 基于CEEMDAN-IBAS-ELM的预测模型Fig.2 Prediction model based on CEEMDAN-IBAS-ELM

4 案例分析

本文研究中的风电功率数据来源于西班牙加利西亚Sotavento风电场。该风电场的采样时间间隔为10 min，额定功率为2 500 kW。以2020年3月1—17日的风电功率实测数据为例进行验证，共2 448个样本点，前2 304个数据作为训练集，最后的144个样本点为测试集。风电功率原始序列，如图3所示。

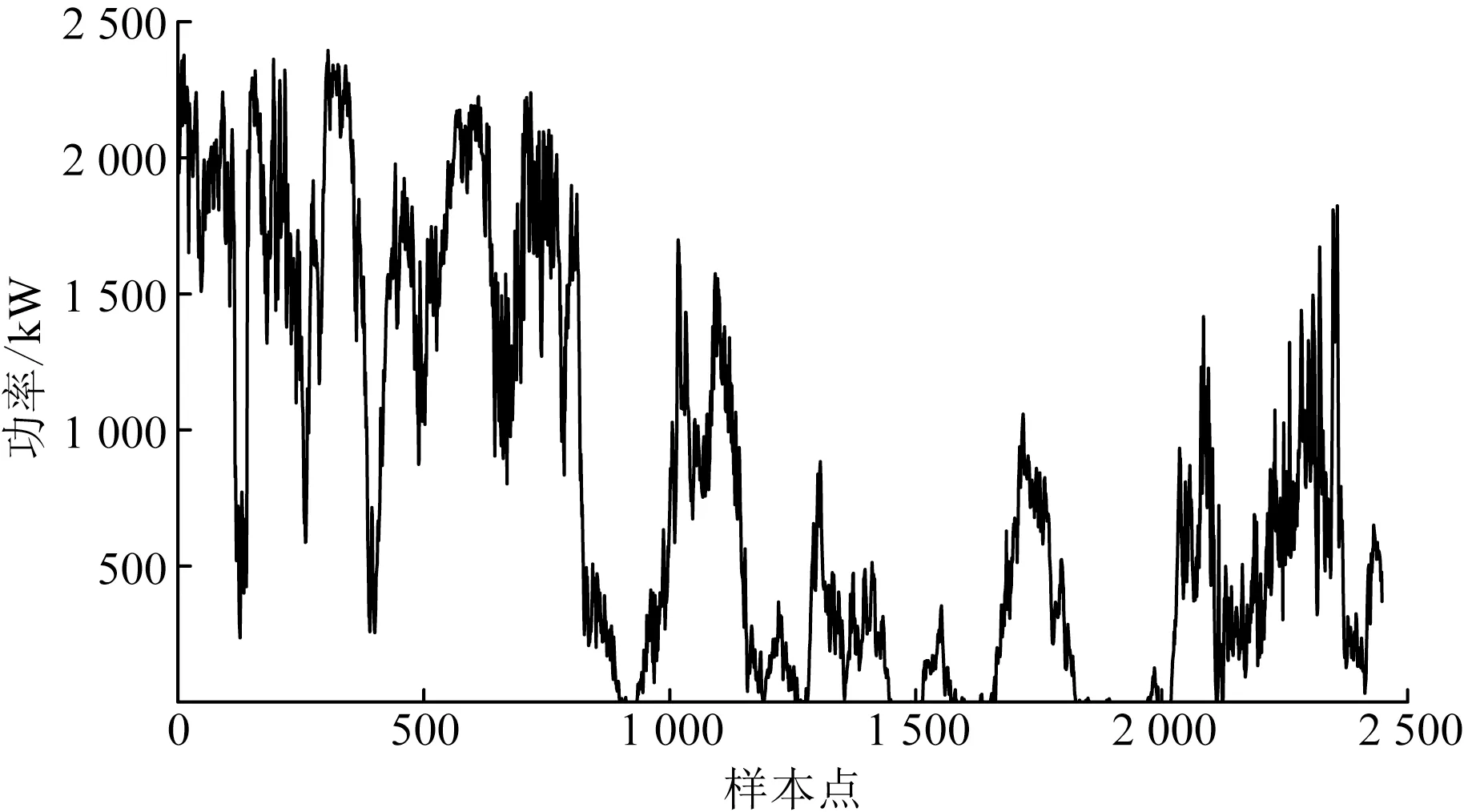
图3 风电功率原始序列Fig.3 Original sequence of wind power

(1)平均绝对误差(MAE)。

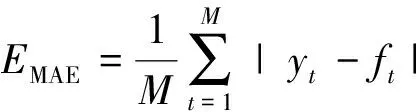
(13)

式(13)中：ft为测试样本中第t个样本的实际值；yt为测试样本中第t个样本的模型预测值；M为对应的样本数。

(2)均方根误差(RMSE)。

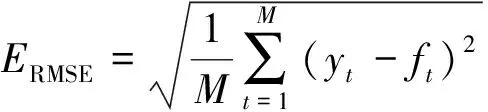
(14)

(3)平均绝对百分比误差(MAPE)。

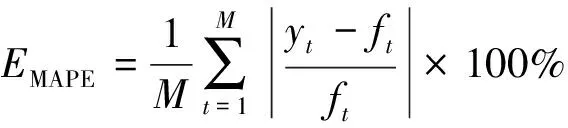
(15)

(4)各个风电功率预测模型各自进行一次预测需要的时间(TIME)，单位为s。

4.1 风电功率序列分解实验

由图3可以看出，原始的风电功率序列的随机性和波动性比较大。使用CEEMD和CEEMDAN分别对原始功率数据进行处理，把数据分解为不同特征尺度下的平稳序列，来提高后续预测模型的准确性。CEEMD和CEEMDAN的参数均选择0.2倍标准差，添加100次白噪声，将原始风电功率数据分为9个IMF分量和一个RES分量。仅放置原始风电功率信号经过CEEMDAN分解后的各功率序列分量，如图4所示。

图4中，RES表示所研究风电功率序列的变化趋势；IMF为风电功率样本的特征分量，按照频率由高到低排列，高频分量波动性比较大，表示风电功率的随机性分量；低频分量具有正弦波特点，表示风电功率的周期性分量。

针对同一原始风电功率序列，分别用CEEMD和CEEMDAN把信号分解为不同特征尺度下的序列分量，再将分解后的各分量进行叠加，重构成一个新序列。用实际功率序列减去重构序列来计算重构误差。采用平均绝对误差MAE和平均绝对百分比误差RMSE来评价重构功率序列与原始功率序列的误差。CEEMD和CEEMDAN的重构误差，如图5所示。

CEEMD的重构误差MAE为2.99×10-13，RMSE为4.25×10-13，而CEEMDAN的重构误差MAE为5.77×10-14，RMSE为1.09×10-13。CEEMDAN分解后的重构误差更小，证明了CEEMDAN可以更好地消除残余辅助噪声，分解能力更加优秀。

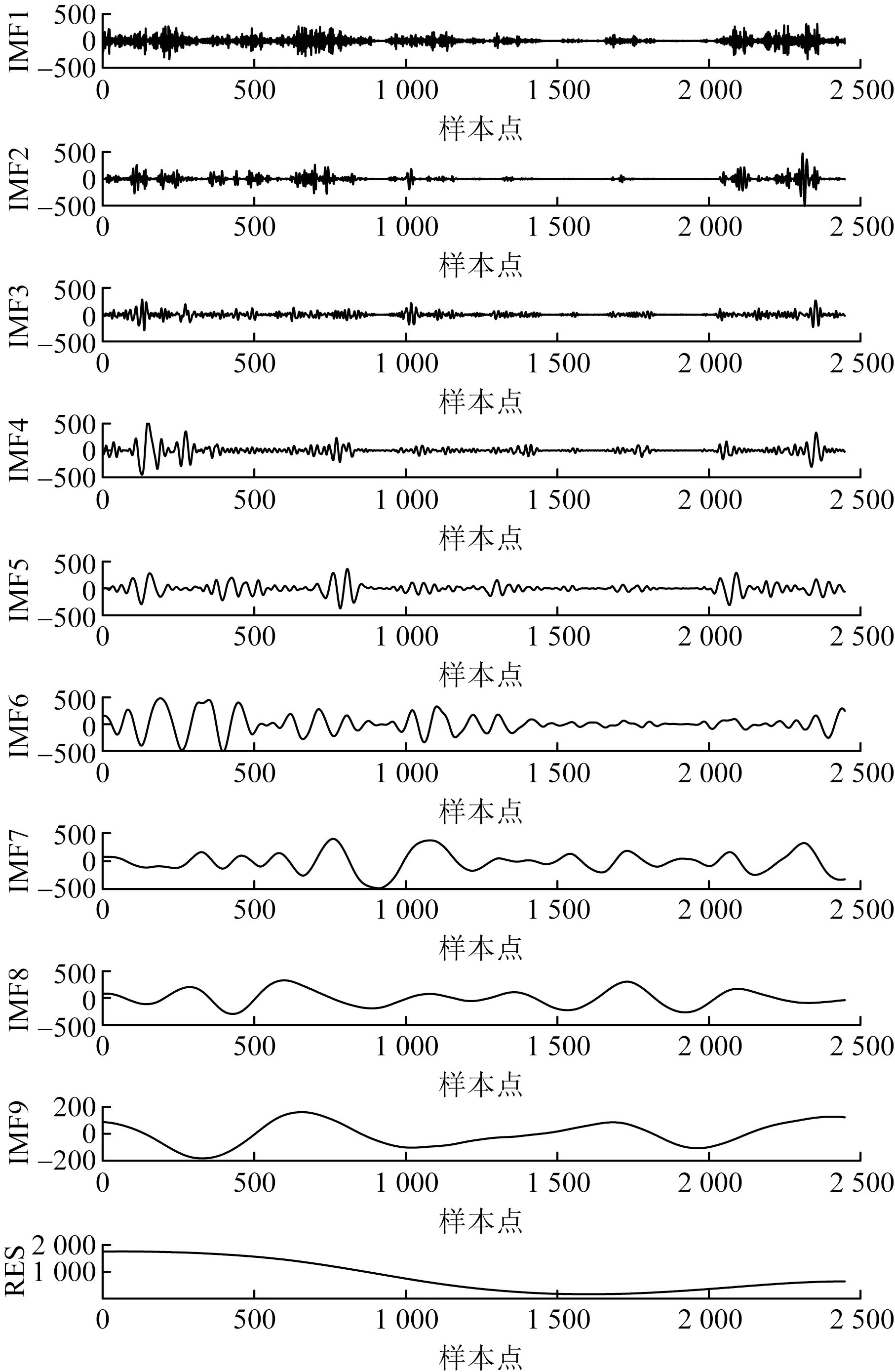
RES为趋势分量 图4 经CEEMDAN分解后的功率序列Fig.4 Power sequence decomposed by CEEMDAN

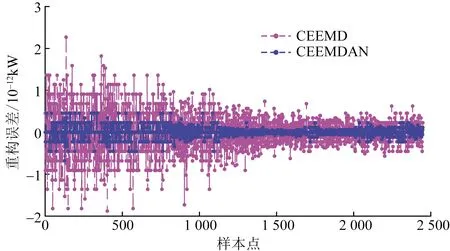
图5 重构误差Fig.5 Reconstruction error

4.2 风电功率预测实验

为了验证本文所提出的预测模型的有效性，搭建了ELM、BAS-ELM、IBAS-ELM、CEEMD-IBAS-ELM、CEEMDAN-IBAS-ELM多种组合模型。还与其他算法优化ELM的预测模型如花朵授粉算法优化的极限学习机(FPA-ELM)、粒子群算法优化的极限学习机(PSO-ELM)以及BP神经网络进行对比，进一步证明所提出的预测模型的有效性。

除IBAS只需要一只天牛外，所有优化算法中最大迭代次数和种群数量均设为100和30。在所有预测模型中，经过CEEMD和CEEMDAN分解的模型运行时间是所有分量序列分别运行的时间之和，其余预测模型运行时间都为进行一次预测运行的时间。

CEEMDAN-IBAS-ELM模型与其他对比模型对风电场2020年3月17日的144个样本点的风电功率进行了预测。基于BAS算法的各组合模型预测结果，如图6所示；基于不同优化算法的组合模型预测结果，如图7所示；2020年3月各预测模型误差评价指标结果，如表1所示。

由表1可以看出，相对于没有模态分解的预测模型，基于模态分解的组合模型的预测精度均有大幅度提升，说明采用信号分解技术可以有效改善预测性能。在所有预测模型中，CEEMDAN-IBAS-ELM模型的预测结果最优，MAE、RMSE、MAPE结果均为最小。与CEEMD-IBAS-ELM相比，MAE下降了30.45%、RMSE下降了33.41%、MAPE下降了27.84%，运行时间也降低了13.31%。说明CEEMDAN的分解效果更加优秀。IBAS-ELM预测模型与BAS-ELM模型相比，MAE下降了6.36%、RMSE下降了5.87%、MAPE下降了5.94%，运行时间基本不变，显示出IBAS的寻优能力更出色。IBAS-ELM与FPA-ELM、PSO-ELM相比，MAE、RMSE、MAPE均是最小，而且运行时间比FPA-ELM降低了84.11%、比PSO-ELM降低了70.12%，运算速度大大提升。显示了IBAS算法的优越性。BP神经网络的性能基本全面落后于ELM网络，表明ELM更适合风电功率预测。

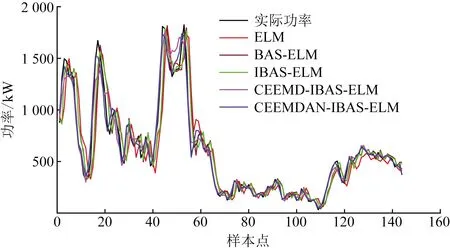
图6 基于BAS算法的各组合模型预测结果Fig.6 Prediction results of each combination model based on BAS algorithm

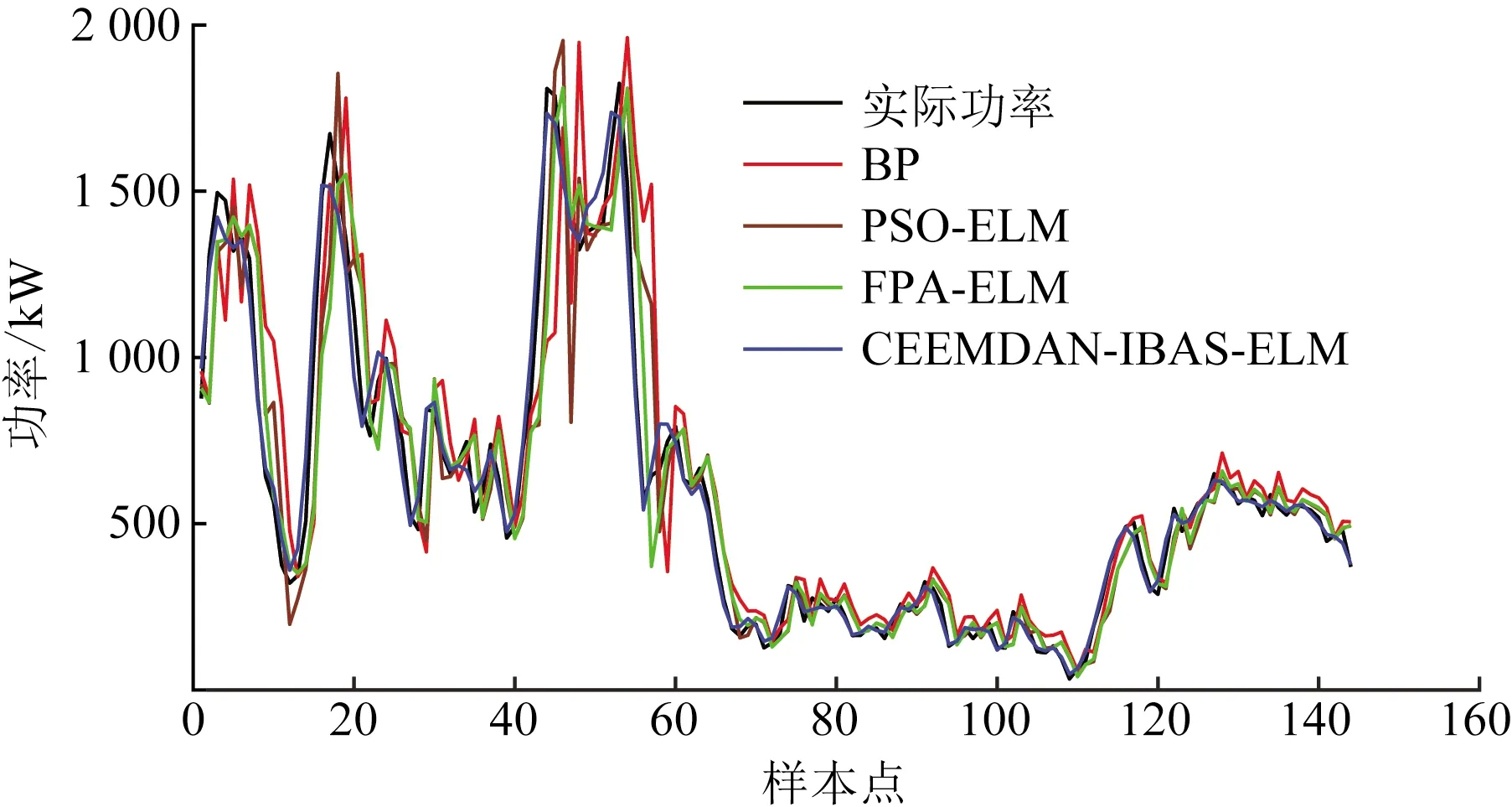
图7 基于不同优化算法的组合模型预测结果Fig.7 Combination model prediction results based on different optimization algorithms

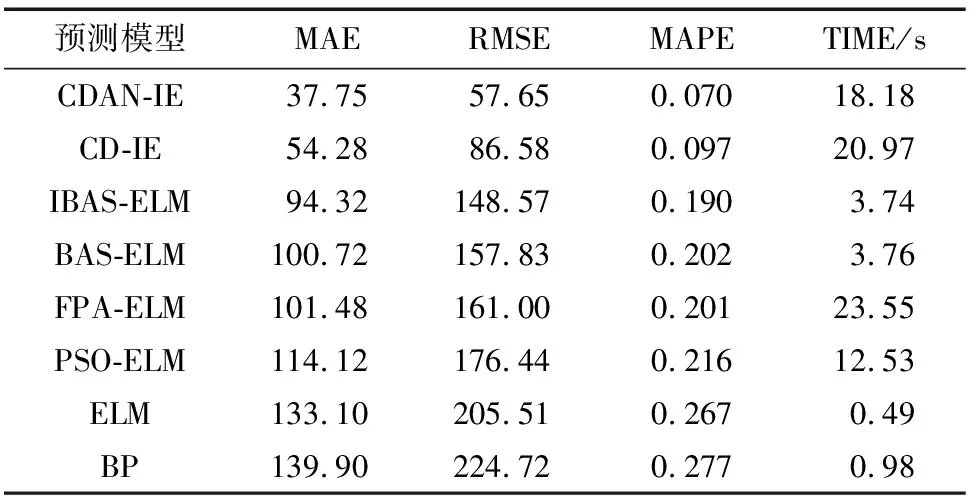
表1 2020年3月模型误差分析Table 1 Model error analysis of March 2020

2020年12月加利西亚Sotavento风电场的额定功率由2 500 kW增加至17 000 kW，为了进一步验证本文提出的CEEMDAN-IBAS-ELM预测模型的准确性和普适性。选取该风电场2020年12月1—17日的风电功率实测数据对该预测模型进行验证，共2 448个样本点，前2 304个样本点为训练集，最后144个数据为测试集。各预测模型对2020年12月17日的144个样本点的风电功率进行了预测。基于BAS算法的各组合模型预测结果，如图8所示；基于不同优化算法的组合模型预测结果，如图9所示；2020年12月各预测模型误差评价指标结果，如表2所示。

由表2可以看出ELM的预测结果更接近于实际值，进一步证明ELM更适合风电功率预测。显然，在所有模型中，CEEMDAN-IBAS-ELM的预测结果最优。与CEEMD-IBAS-ELM相比，MAE下降了55.08%、RMSE下降了59.88%、MAPE下降了41.37%，运行时间也降低了14.66%。进一步证明了CEEMDAN分解效果更加优秀。此外，IBAS-ELM与BAS-ELM相比，MAE下降了3.32%、RMSE下降了4.73%、MAPE下降了3.13%，运算时间基本不变。进一步显示出对BAS算法的优化效果。与FPA-ELM、PSO-ELM相比，不仅三个误差评价指标均为最小，而且运行时间比FPA-ELM降低了84.23%，比PSO-ELM降低了70.21%。进一步证明了显示了IBAS算法的优越性。

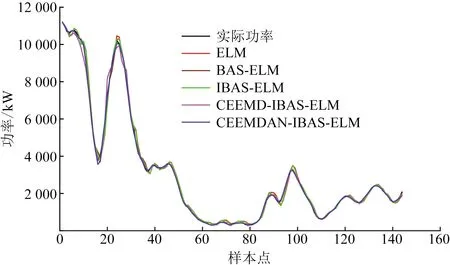
图8 基于BAS算法的各组合模型预测结果Fig.8 Prediction results of each combination model based on BAS algorithm

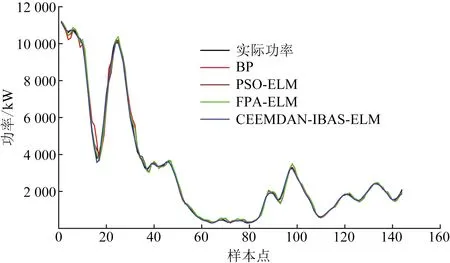
图9 基于不同优化算法的组合模型预测结果Fig.9 Combination model prediction results based on different optimization algorithms

表2 2020年12月模型误差分析Table 2 Model error analysis in December 2020

5 结论

针对风电功率具有很强的波动性和间歇性、预测误差大的问题。提出了一种CEEMDAN-IBAS-ELM的预测模型，大大提高了风电功率预测的准确度。研究结论如下。

(1)引入了动态惯性权重，改变了天牛的位置更新方式，使天牛的局部搜索能力得到加强，提高了BAS算法的优化能力。

(2)采用CEEMDAN对原始数据进行预处理，把原本非平稳、非线性的复杂功率数据，分解为多个简单序列。减少了原始数据的波动性和随机性，为后面模型的准确预测奠定了基础。

(3)利用IBAS对ELM进行寻优，找到最优权值和阈值并赋给ELM,分别建立分解序列的ELM预测模型，最后叠加各序列的预测值得到最终预测结果。

(4)使用MAE、RMSE、MAPE以及算法运行时间四个评价指标对各模型的预测结果进行分析。与其他预测模型相比，CEEMDAN-IBAS-ELM模型的MAE、RMSE、MAPE均为最小，且算法运行速度快，可以看出本文提出的预测模型预测精度高且运行时间短，可以很快获得预测的功率，便于电网进行电力调度和设备检修。