基于长短期记忆法的换流站阀冷系统参数预测
2022-02-17王凌云杨雨琪史磊刘钊
王凌云, 杨雨琪, 史磊, 刘钊
(1.三峡大学电气与新能源学院, 宜昌 443002; 2.国网宁夏电力有限公司, 银川 750001; 3.国网宁夏电力有限公司检修公司, 银川 750001)
随着特高压直流输电的快速发展,已经有众多的特高压直流输电线路应用到中国的电力系统中。在换流站交直流转换方面涉及各个环节的关键设备,其中换流阀占据重要的地位。由于通态平均电流较高,换流阀在工作过程中会形成较多的热量,其中,阀冷系统对于换流阀的正常运行发挥了重要的作用,它能够保证阀组运行在合适的温度范围内。伴随2005年第一套国产化灵宝背靠背直流工程投运成功,换流阀在中国得到有力发展。为了保证阀冷系统在全生命周期内的可靠性,根据《国家电网公司直流换流站检测管理规定》等条例的要求,换流站每年需要对阀组进行全面测试,并定时对内冷水流量、进出阀温度、主泵及回水压力等运行参数进行抄录。在数据收集的过程中,时常会发生采样错误,对基于深度学习的数据挖掘过程造成不可忽视的影响。
另外,通过对历史采样数据研究发现,阀冷系统中监测到的各类参数与电力负荷相类似,大时段内存在规律性,小时段内又具有随机性,是典型的时间序列数据。基于上述属性,如果能在完善数据集的基础上实现对换流阀冷却系统运维环节中部分关键参数的有效预测和判断,便可以更深一步挖掘分析阀冷系统的运行状态及冷却能力。
文献[1-2]根据换流站冷却系统日常运维的实际需求,进行包含系统关键参数的仿真建模,旨在对阀冷系统运行时各个设备的参数变化进行智能判断,同时实现工况预测和故障诊断等功能,但是该模型侧重于仿真模拟,只能对现有的参数进行输入分析,并不能发现阀组运行中潜在的问题。另外,基于换流站日常运维产生的大量监测数据也展开了相应的研究分析[3-5]。文献[6-9]研究的内容主要包括了阀冷系统漏水研究、冷却能力分析、逻辑控制研究、保护值整定计算等,但都侧重于设备状态分析,无法对阀冷系统的性能进行有效预测和判断。
在预测算法方面,文献[10]研究了城市用电量与季节、环境温度、节假日、风速等因素的相互关系,并在用电预测的分析建模中引入了长短期记忆网络(long-short term memory,LSTM)。文献[11]成功将LSTM方法应用于风力发电功率的预测中,并将人工神经网络与支持向量机网络的优缺点进行分析对比,证明在时间序列处理中采用LSTM可以达到较好的效果。文献[12-13]也指出,将LSTM方法应用到电力负荷预测中,能够得到较为准确的预测结果。但目前为止,关于换流站阀冷系统各环节关键参数的预测研究较少,LSTM在处理时序属性数据方面的优势也未能在换流站中充分体现。
基于上述分析,现以宁夏某换流站阀冷系统的运行参数为例,基于均值填补法对回水压力、进出阀温度等进行处理,然后进行特征参数提取的过程。该过程主要利用主成分分析法(principal component analysis, PCA),同时结合LSTM网络学习时间维度特征,建立基于PCA-LSTM的换流站阀冷系统时序运行参数预测模型,实现系统冷却能力的分析与故障判断,以期帮助换流站运维人员提前发现并及时处理系统存在的隐患,使换流站阀冷系统能够获得更高的安全性。
1 换流站阀冷系统构成及工作原理
阀冷系统总体划分为三个部分,分别为外冷水系统、内冷水系统、阀冷控制系统,各个部分的功能存在一定的差异性。具体介绍如下。
内冷水系统主要利用液态水的流动带走换流阀产生的热量,其中冷却介质是去离子水(电导率低于0.5 μS/cm,纯度较高)。在结构上,整个系统划分为主水、稳压以及水处理三大回路。其中主水回路内包括换热器以及换流阀等部分;稳压回路能够维持压力的稳定性,并对水容积变化进行缓冲,主要包括氮气瓶与膨胀管;水处理回路能够将水中的离子等物质进行过滤,确保内冷水处于较高的质量,一般包括补水泵以及交换器等设备。
外冷水系统包括喷淋泵以及冷却塔等结构,可以对内冷水进行冷却,从而达到温度的要求。该系统在运行过程中,可以将喷淋泵进行蒸发,使得换热盘管表面具有适量水分,在水分蒸发过程中可能带走一定的热量,基于这种方式降低阀内冷水的温度,并再次流动到换流阀中。
阀冷控制系统具有设备运行状态监控等功能,可观测到的参数包括电导率、温度以及压力等,同时还能够对冷却塔以及阀门的运行状态进行监测,一旦发现异常状况可以及时报警,确保各部分处于稳定的工作状态。该系统的核心控制部分基于可编程逻辑控制器(programmable logic controller, PLC)实现,可以控制内、外冷水系统使各项参数运行在稳定工况下。当控制系统监测到上述参数值严重异常时,PLC将输出跳闸保护,向阀控发出闭锁请求。换流站阀冷系统整体结构如图1所示。
通信系统主要与数据传输的过程有关,它可以实现报警量以及设备运行参数等信息的发送功能。其中阀冷控制系统内流量、压力、液位和温度变送器等仪表传感器由PLC控制系统进行控制与监测,从整体上实现阀冷却系统的全自动运行[14]。
2 阀冷系统运行参数预处理
2.1 数据预处理
在对换流站阀冷系统运行参数进行周期性采样的过程中,可能出现的数据缺失问题一般与人为操作失误以及设备故障有关。在文献[15]之后定义了不同类型的数据缺失机制,并提出了针对性的处理方法,如缺失填充、元组删除等。当对阀冷系统的运行参数进行分析时,基于时间序列的采样数据分析对样本连续性要求较高,删除部分数据对整体样本集特征的研究会产生不利影响。因此,采用填补类型中的均值填补法对换流阀运行参数进行处理。
均值填补法主要利用精度、方差、标准差等概念进行数学分析。
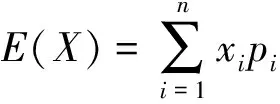
(1)
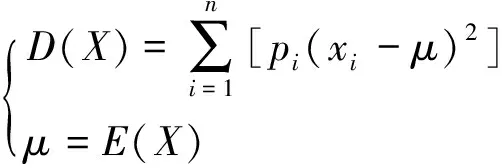
(2)
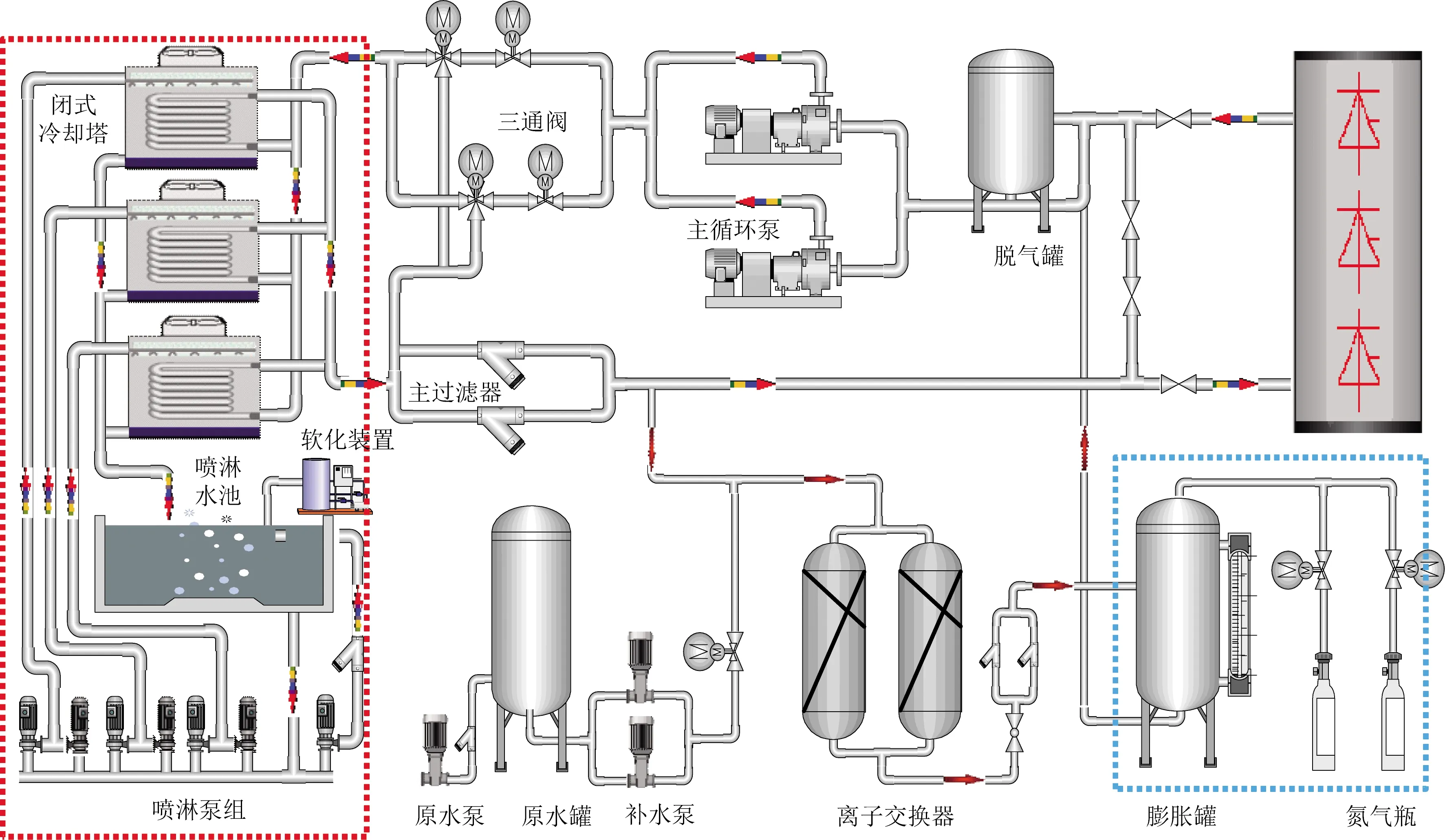
图1 换流阀冷却系统工艺结构图Fig.1 Structure of cooling system of converter valve
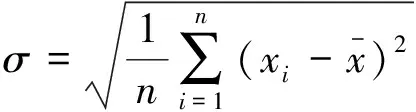
(3)
均值填补法的应用具有一定的优势,如果已经明确变量类型以及属性信息,则处理难度较低,并且能够达到较高的精度要求,可以满足实际需求。具体算法步骤如图2所示。
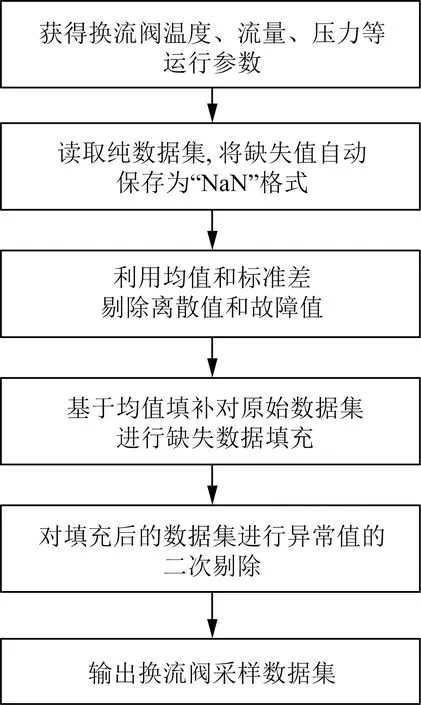
图2 均值填补法算法步骤图Fig.2 Algorithm steps of mean filling method
2.2 算法实例
通过采集宁夏某换流站2019年10月—2020年9月极一低端换流阀组进出阀温度、冷却水流量、主泵出水压力及回水压力抄录数据发现,原始采样集由于设备传感器故障,导致数据存在片段状缺失以及明显数值异常。基于此,采用优化后的均值填补法对上述参数进行了批量处理。数据处理结果如图3~图5所示。
由图3~图5可以看出,经过均值填补法处理后的4类参数范围皆符合换流站阀冷系统正常运行要求。
选择合适的模型评价指标,采用均方根误差(root mean squard error, RMSE)对缺失属性的预测偏差进行评价。如果该指标较大,则说明采用的模型在数据描述上存在较大的偏差;而如果该指标较小,则说明精度较高。
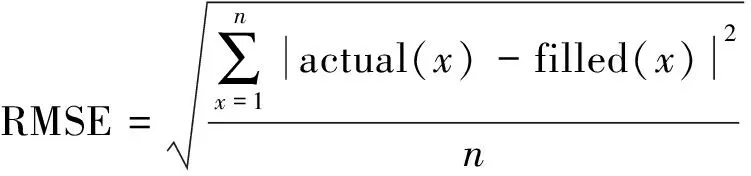
(4)
式(4)中:n为x在不同取值下,样本集中所填充数据的个数;actual(x)为实际值;filled(x)为填充值。
由于在真实测量场景下的n是有限的,一般通过“最可信赖值”来取代真实值。处理之后的主泵出水压力、进出阀温度、回水压力和冷却水流量数值与系统实际运行最优值之间的RMSE结果(均值填补法)如表1所示。

图3 进、出阀温度采样值处理Fig.3 Temperature sampling value processing of inlet and outlet valves
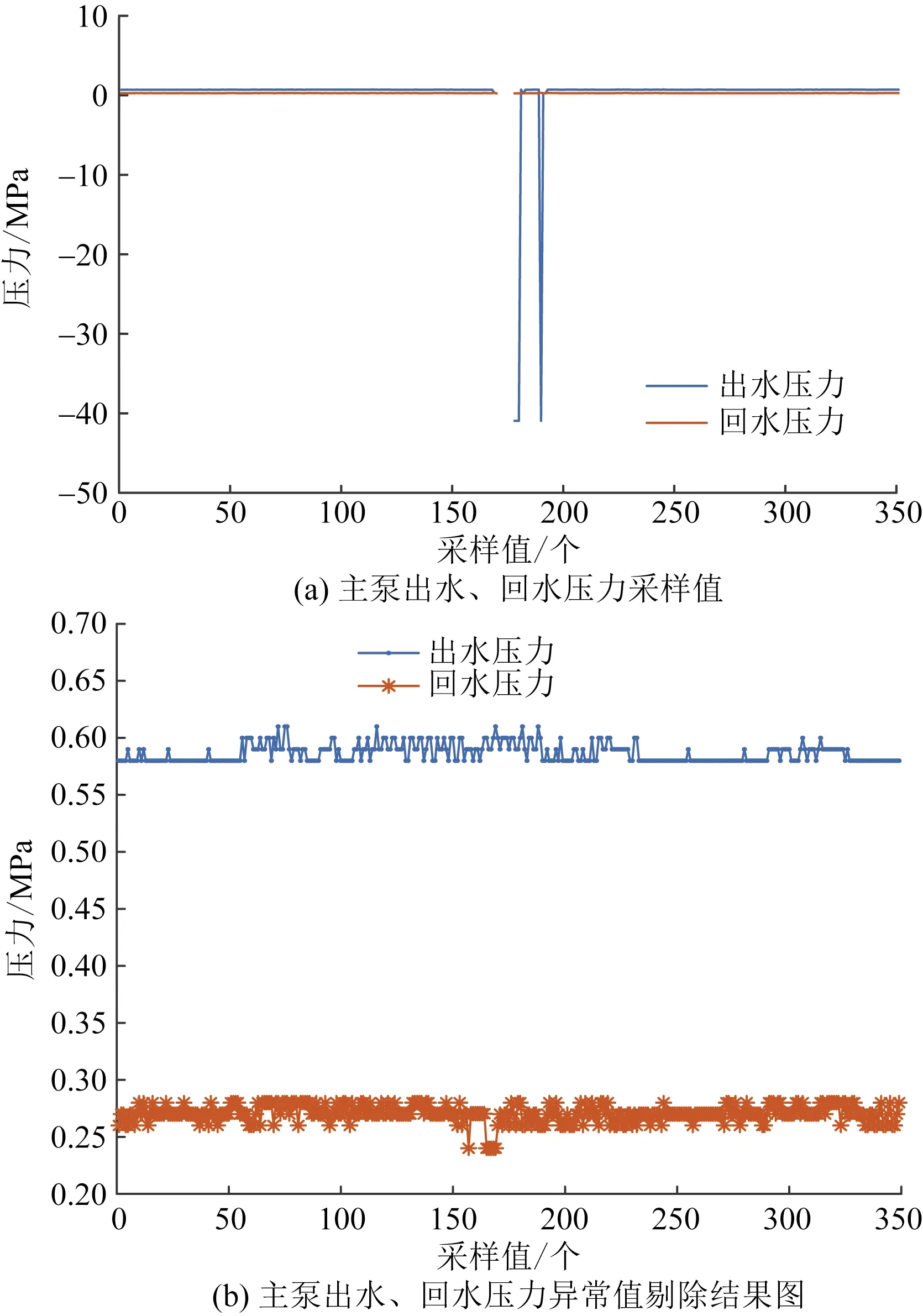
图4 主泵出水压力及回水压力采样值处理Fig.4 Treatment of sampling value of outlet pressure and return water pressure of main pump
由表1可知,所求RMSE皆符合模型精度评价标准,同时满足阀冷系统运行要求。
综上可得,采用的数据处理方法可以对阀冷系统中的异常数据进行有效识别,并对缺失数据实现高效准确的填充,为下一步阀冷系统关键参数的预测和应用提供了完整而可靠的数据基础。
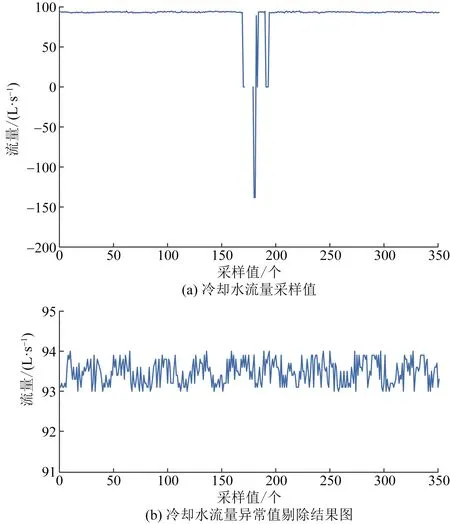
图5 冷却水流量采样值处理Fig.5 Treatment of sampling value of cooling water flow
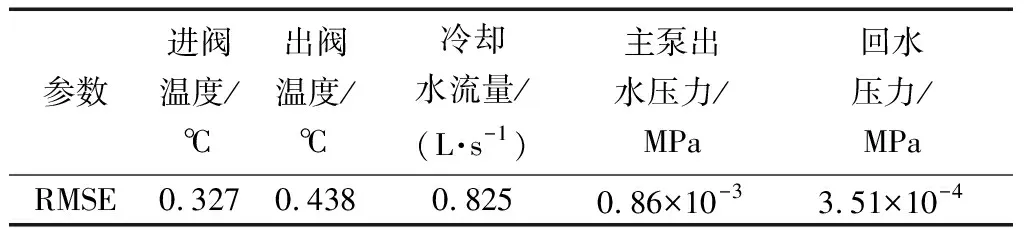
表1 模型评价结果Table 1 Model evaluation results
3 基于PCA-LSTM网络的阀冷系统时序参数预测模型
为进一步挖掘和利用换流站阀冷系统潜在的数据信息,利用系统运行采样数据的时序性,以完善后的样本集为基础,对阀冷系统关键运行参数进行预测,从而对换流阀的冷却能力进行有效评估,为换流站的维护提供准确的信息,使其能够保持最佳且安全的运行状态。
3.1 相关性分析
阀冷系统采集到的内冷水流量、环境温度、出入水温度、回水压力和主泵出水压力等监测数据之间有着一定的相关度。因此,基于PCA方法来分析指标的相关性,以此将大量的指标简化为少数关键指标进行分析,提高了计算的效率,降低了模型的复杂度,且对计算结果的精度产生的影响可忽略不计。
计算过程如下。

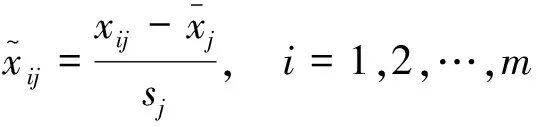
(5)
(6)

(7)

(2)相关系数矩阵R的计算。
R=(rij)m×m
(8)
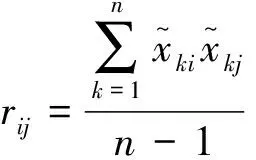
(9)
式中:rii=1;rij=rji;rij为第i个指标和第j个指标的相关性系数;i,j=1,2,…,m。
(3)特征值和特征向量的计算。按照高低顺序排列特征值,得到R的特征值有λ1≥λ2≥…≥λm≥0,而u1,u2,…,um即为特征向量,uj=(u1j,u2j,…,unj)T,由此可以得到的指标变量为
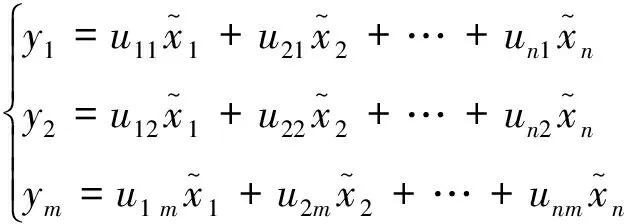
(10)
式(10)中:y1为第1主成分;ym为第m主成分。
(4)计算主成分贡献率及累计贡献率。选取特征值λ1,λ2,…,λm所对应的前p个主成分(m≤p),并对评价结果进行计算,具体公式为

(11)

(12)
式中:bj为主成分yj的信息贡献率;ap为主成分y1,y2,…,yp的累计贡献率。如果αp基本等于1(αp=0.85,0.90,0.95),那么可以直接将前p个指标作为主成分,在此基础上进行后续计算。
(5)计算综合得分。
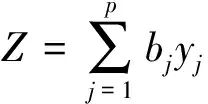
(13)
式(13)中:Z为综合得分值;bj为第j个主成分yj的信息贡献率。
根据上述算法流程,输入换流站阀冷系统的入水温度(x1)、环境温度(x2)、主泵出水压力(x3)、回水压力(x4)、冷却水流量(x5)5项指标进行训练。最终得到的相关系数矩阵,如表2所示。
由表2可以得出每两个指标之间的相关性。与入水温度相关系数最高的是冷却水流量;与环境温度相关度最高的是入水温度;主泵出水压力与回水压力相互拥有最高的相关度;与冷却水流量相关度最高的是主泵出水压力。
如表3所示,前3个主成分的累积贡献率达到了86.769 4%>85%(将PCA的贡献阈值设为85%),所以在后续研究中只需要选择前3个主成分,基于这种方式实现了降维处理,从而简化计算,提高了计算的效率。计算所得因子得分矩阵如表4所示。
(1)第1主成分y1的表达式中,在标准化变量主泵出水压力(x3)和回水压力(x4)中有较大的正载荷,因此可以认为y1是压力的综合成分。
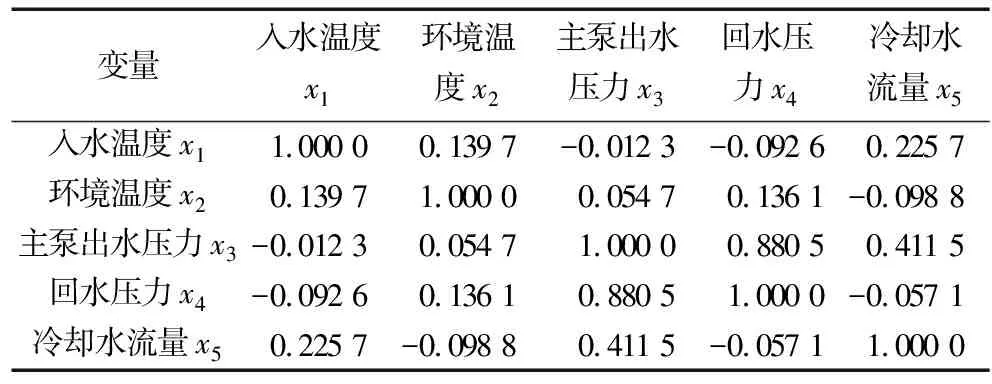
表2 相关系数矩阵Table 2 Correlation matrix
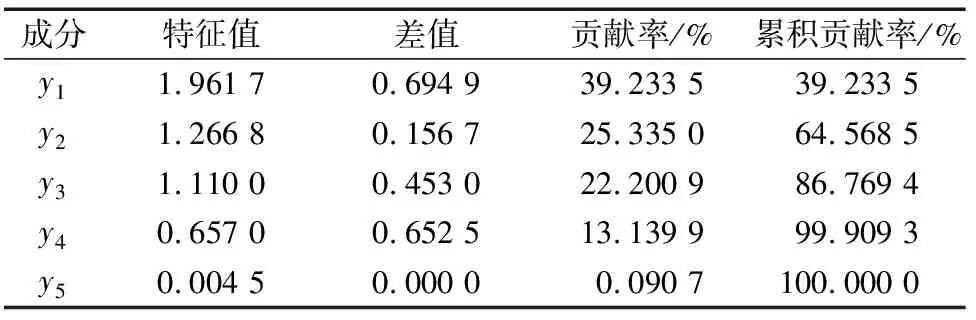
表3 主成分表达式系数矩阵Table 3 Principal component expression coefficient matrix

表4 因子得分矩阵Table 4 Factor score matrix
(2)第2主成分y2的表达式中,在入水温度x1和冷却水流量x5中有相近且较大的正载荷。通过对运维数据的调查研究和相关资料可知,在换流阀温度、风机转速一定时,内冷水入水温度与阀冷系统冷却效果成反比,即入水温度越高,冷却系统冷却效果越差,换流阀能够继续承受的负荷越少,因此可以认为阀冷系统的冷却能力能够近似通过内冷却系统的入水温度直观反映。故可认为第2主成分y2是冷却能力的协调成分。
(3)第3主成分y3的表达式中,在入水温度x1和环境温度x2中有比较大的正载荷,可以认为第3个主成分y3是温度成分。
3.2 时序数据预测方法
蕴含时序属性的数据预测分析是一类较为复杂的预测建模问题,在众多预测算法中对蕴含时序属性的数据应用较多的方法主要有:周期因子法、传统时序建模方法(如自回归移动平均模型、差分自回归移动平均模型等),此外还可以利用LSTM模型等针对数据组织方式进行调整。RNN(recurrent neural network)网络引入了时序概念[16],使得网络的适用性明显提高,便于对时序属性数据进行处理,在RNN的众多变体中[17],LSTM作为其中之一,解决了循环神经网络存在的诸多不足,如梯度爆炸等,便于应用长距离的时序信息。
3.3 长短期记忆网络
LSTM方法在网络中融入了sigmoid函数和双曲正切函数,通过求和操作等实现数据的长期保留,所以在应用中显示出明显的优势。
该网络模型基本结构如图6所示。其运行流程可大致分为4部分。
(1)“遗忘门”[18]共有σ层,输入Ct-1、xt,然后在Ct-1输出特定的值,处于0~1范围内;其中0、1

xt为模型输入;ht为模型输出;Ct为传递神经元细胞状态; tanh函数为激活函数图6 LSTM网络结构图Fig.6 LSTM network structure diagram
对应着两个特殊的状态,分别是完全遗忘、完全保留;具体公式为
ft=σ(wf[ht-1,xt]+bf)
(14)
式(14)中:ft为t时刻的遗忘门;σ为sigmoid函数;xt、ht-1分别为t时刻和t-1时刻的输入层和隐藏层输出;wf为对应的权重矩阵;bf为对应的偏置项。
(2)“输入门”选择模型所需要的数据。该门的σ层决定要更新的数值,由双曲正切层生成一个新的候选数值并增加到神经元状态中。
it=σ(wi[ht-1,xt]+bi)
(15)
C′t=tanh(wc[ht-1,xt]+bc)
(16)
式中:it为t时刻的输入门;C′t为更新后的神经元细胞状态;wi、wc为对应的权重矩阵;bi、bc为对应的偏置项。
(3)执行神经元状态更新的过程,即从Ct-1到Ct,将ft与旧状态进行相乘,添加新候选值,公式为
Ct=ft⊙Ct-1+it⊙C′t
(17)
式(16)中:Ct为t时的细胞状态。
(4)“输出门”决定最后的输出值[19]。
Ot=σ(wο[ht-1,xt]+bο)
(18)
ht=Ot⊙tanh(ct)
(19)
式中:Ot为t时的输出门;⊙为矩阵元素相乘[20];wo为对应的权重矩阵;bo为对应的偏置项。
3.4 算法实例
在当前换流站阀冷系统的运维工作中,当监测系统观测到相关设备的运行参数超出保护整定值时,系统会进行故障报警;但若运行参数值在保护定值范围内,系统便无法准确作出判断,此时若是出现其他问题或者记录设备状态,便只能以运维人员的经验为依托进行记录或是判断;同时,各类仪器提供的大量设备实时监测数据也并未得到合理充分的利用,多数情况下对设备寿命以及运行能力的判断仍然根据运维人员的经验或者是生产厂家依据相关规定设定的告警值。
结合当前运维实际和PCA分析结果,在风机开机台数固定且转速保持一致的条件下,保留冷却水流量为LSTM模型输入,实现对内冷系统入水温度的预测,从而对换流阀整体的冷却能力进行判断。具体算法结构如图7所示。
整个框架包含了数据预处理、输入层、隐藏层、输出层4个功能模块,预处理模块负责对阀冷系统几类运行参数进行基于均值填补的缺失值处理和基于PCA的指标参数降维,将得到的简化后的标准数据传递给输入层,输入层将接收到的数据划分为训练数据集和测试数据集,隐藏层基于LSTM(图6)构建网络模型,最后将预测的结果输出[21]。
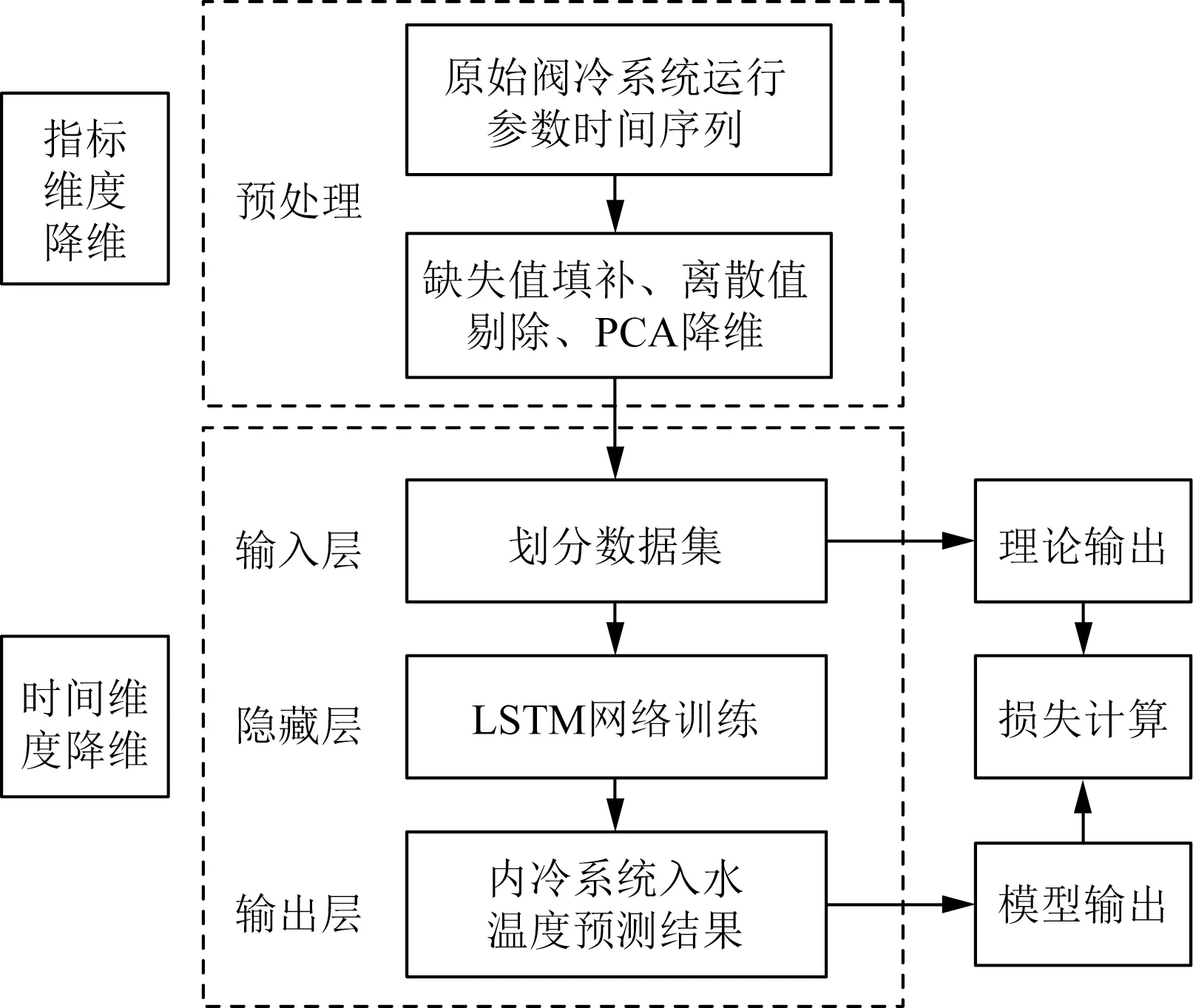
图7 基于PCA-LSTM的时间序列预测结构图Fig.7 Time-series prediction structure chart based on PCA-LSTM
由于在同一个换流站中存在构造相同但接线端口不同的阀组,当运行工况相同时,不同阀组的相同项参数在数值和变化趋势方面一般差别较小。基于此,在得出某台阀组内冷系统的入水温度预测结果后,可以与其他阀组的运行参数进行横向对比。若某一阀组内冷系统的入水温度比其他阀组高,或者在某一时间段内的数值上升速率过快,则表明该阀组的冷却能力在下降,即系统中可能存在某些故障,需要运维人员进行检修。
以宁夏某换流站极一低端换流阀组2019年10月—2020年9月的冷却水流量和内冷水入水温度两项共2 728组运行参数为模型输入,选取数据总量的90%作为训练集,10%作为验证集,基于PCA-LSTM方法进行仿真建模,并同ARIMA模型进行对比,两类模型的输入数据皆由相同历史数据集生成,预测结果如图8所示。
图8为采用PCA-LSTM和ARIMA模型在300个和3 000个数据集的训练中得到的进阀温度预测曲线。
图9为预测模型结果对比图。经过对图10中实际进阀温度曲线和采用上述两种方法进行预测的结果曲线对比分析可知, 建立的PCA-LSTM预测模型相比ARIMA而言具有更佳的预测效果。选择指标进行评价,主要有RMSE、平均绝对百分比误差(mean absolute percentage error,MAPE)两项指标,具体的计算结果如表5所示。
由表5可知,在对换流站阀冷系统入水温度进行预测的过程中,本文中建立的PCA-LSTM模型有着更高的精度,其MAPE比ARIMA模型少了0.508%,同时能够准确实现阀冷系统入水温度的预测,有效帮助运维人员提前发现隐患并及时解决问题,避免发生更加严重的后果。
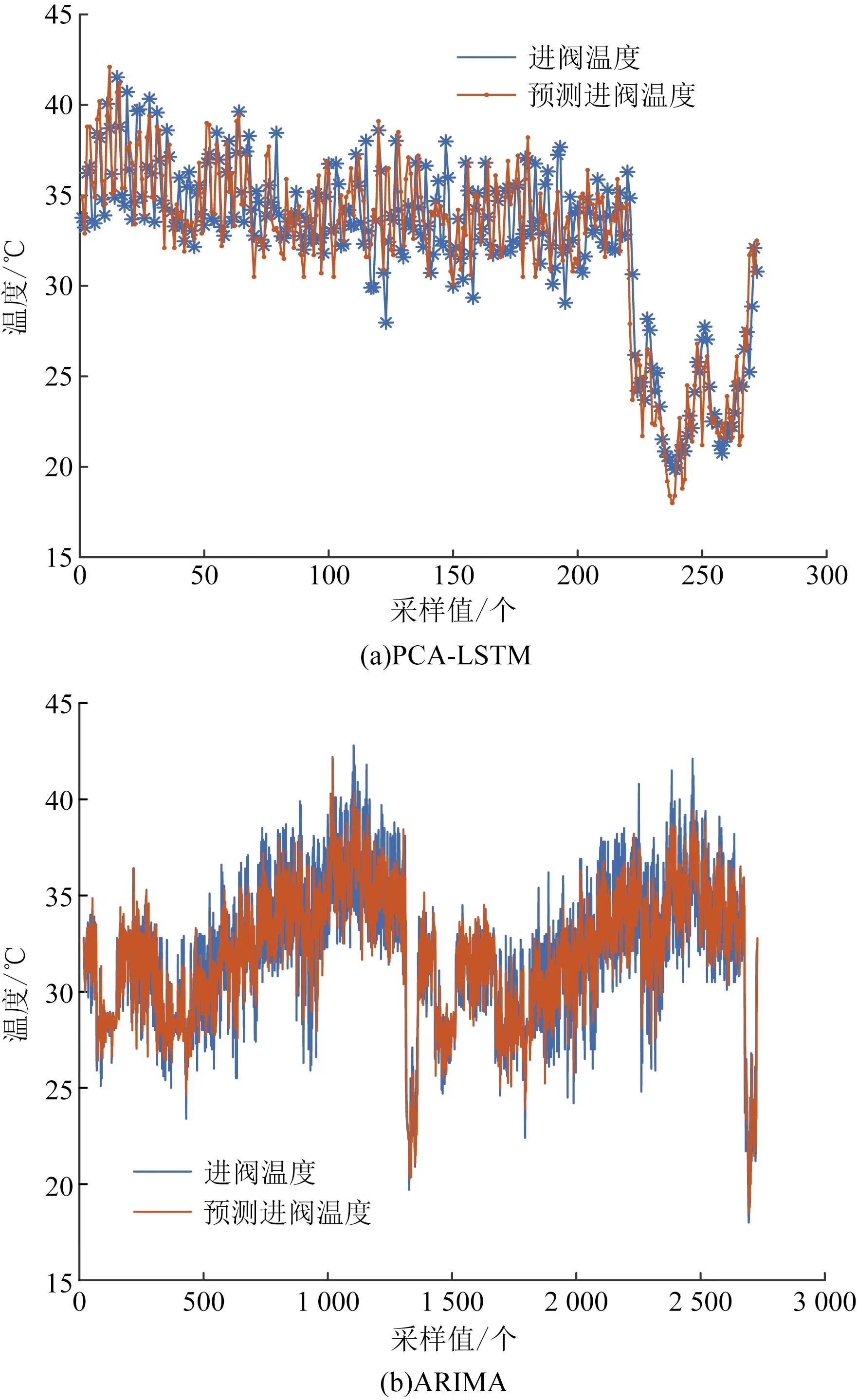
图8 PCA-LSTM和ARIMA预测结果图Fig.8 Prediction result chart of PCA-LSTM and ARIMA
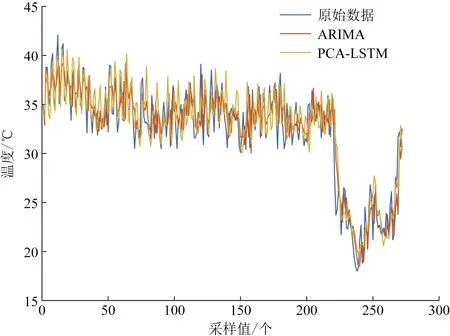
图9 模型预测结果对比图Fig.9 Comparison chart of model prediction results

表5 模型预测结果比较Table 5 Comparison of model prediction results
4 结论
提出了一种基于PCA-LSTM网络的预测方法,通过对换流站阀冷系统入水温度的有效预测判断换流阀的冷却能力,帮助运维人员提前发现并及时解决系统隐患。通过实际算例分析,可以得出以下结论。
(1)基于均值填补法实现了阀冷系统运行参数中异常值的修正和缺失数据的填补,使样本采样集更加贴合换流阀实际运行情况。
(2)在完整可靠样本集的基础上,采用PCA对多维影响因子进行降维,从而改善了单一LSTM网络易造成过拟合的情况。
(3)在所建立的ARIMA、PCA-LSTM两种模型中,采用后者得到了更佳的预测结果,对应的MAPE为4.96%。
综上,所建立的模型能够有效应用于换流站阀冷系统冷却能力的预测,从整体上提高了阀冷系统运行的安全性、稳定性,同时提高了换流站相关保护检修工作的质量和效率。
