基于特征工程的集成学习短期光伏功率预测
2022-02-17崔树银汪昕杰
崔树银, 汪昕杰
(上海电力大学经济与管理学院, 上海 200090)
如今,越来越多的国家为了达到环境保护的目的而加大对可再生能源的利用。目前,光伏(photovoltaic,PV)发电系统已在世界范围内得到广泛使用,其装机容量逐年增加。根据中国电力调度部门规定[1]光伏发电功率预测根据时间分为短期预测和超短期预测,准确的短期光伏功率预测对于电网稳定运行、园区综合能源管理及可再生能源消纳都具有一定意义[2]。
目前,针对短期光伏功率预测的方法还是以数据驱动[3]为主,并主要分为两种:传统的统计方法和现代人工智能方法。传统的统计方法普遍是通过已有的历史数据,来提取光伏输出功率与天气因素之间的相关性进行预测。文献[4]通过分析光伏发电与地理位置和天气因素之间的相关性,建立光伏发电时间序列模型进行预测。文献[5]提出一种马氏距离相似度量的方法来选取相似日,结果表明,预测精度较高。与传统的统计方法相比,现代人工智能方法更适合处理光伏输出功率与影响因素之间的非线性关系。文献[6]分别用长短时记忆网络和深度置信网络进行训练,再将各模型的训练结果进行动态结合,结果表明,预测精度良好。文献[7]首先通过变分模态分解将光伏输出功率分解为不同频率的分量,再使用长短时记忆网络进行预测。近年来,越来越多的研究表明多模型融合比单一模型能取得更好的预测精度。文献[8]将多种神经网络模型进行融合,来对超短期母线负荷进行预测,结果表明,相较于各单一模型有更高的预测精度。
综上所述,现提出一种在Stacking集成学习框架下融合Bagging和Boosting算法的短期光伏功率预测模型。利用Copula函数的相关性分析和轻量级梯度提升机的特征贡献度计算来进行特征筛选;选取泛化性能较优的模型作为基学习器,并采用贝叶斯优化算法来对基学习器模型参数进行优化;定义一个超级学习器,并采用5折交叉验证,将基学习器和元学习器封装到超级学习器中训练;采用澳大利亚太阳能中心的艾丽丝泉光伏站数据来验证模型的准确性。
1 特征工程
光伏输出功率不仅受到天气因素的影响,如温度、湿度、风速、辐照角度等,还受到光伏板内部因素的影响,如电压、电流、转换效率[9]等。可见,光伏输出功率受到的影响因素较多。因此,利用Copula函数来对影响因素进行相关性分析,再通过轻量级梯度提升机的特征贡献度计算来进行特征筛选。
1.1 Copula函数
Copula函数的思想就是把边缘变量转化为均匀分布变量,再把相关性定义为一个在均匀分布之上的联合分布[10]。根据Sklar定理[11],设H为n维变量x1,x2,…,xn的联合分布函数,那么其对应的边际分布则分别为F1,F2,…,Fn;n元Copula函数C的表达式为
H(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]
(1)
若F1,F2,…,Fn是连续的,则C唯一;反之,如果F1,F2,…,Fn为边缘累积分布函数,C为相应的Copula函数,则由式(1)定义的函数H为F1,F2,…,Fn的联合分布函数。
1.2 基于Copula函数的相关性分析
通常使用皮尔逊相关系数(Pearson)、斯皮尔曼秩相关系数(Spearman)、肯德尔秩相关系数(Kendall)来量化样本之间的相关程度。传统的相关性分析方法对于样本变量的要求较高,且主要分析变量间的线性关系,而由Copula函数导出的相关系数可以很好地描述变量之间的非线性关系。
选取由Copula函数导出的Spearman相关系数,来分析光伏输出功率与影响因素之间的非线性关系。假设两个随机变量X和Y,与两者对应的分布函数为P(x)和Q(x),则由Copula函数C(u,v)得到的Spearman相关系数ρ的计算式为
(2)
式(2)中:u和v分别为两个随机变量的边缘分布函数P(x)和Q(x);其中ρ的值越大,表示变量之间的相关性越显著。
常见的Copula函数有这几种,分别为Normal-Copula、t-Copula、Frank-Copula、Gumbel-Copula、Clayton-Copula[12]。选取最优Copula函数是准确进行相关性分析的前提条件。通过计算经验Copula函数与各个备选Copula函数之间的欧式距离,最优Copula函数选择欧式距离最小的备选Copula函数,并计算出其相应的相关系数。
最优Copula函数选取流程如下:①求出变量的边缘分布,根据边缘分布函数求出各个备选Copula函数的参数估计值;②计算变量的经验分布函数,并求出原始样本点的经验分布函数值;③计算各个Copula函数对应的Spearman相关系数;④根据步骤②的经验分布函数值,再计算出原始样本点的经验Copula函数值,以及各个备选Copula函数值;⑤计算两者的欧式距离,选取最小者为最优Copula函数。
欧式距离的表达式为
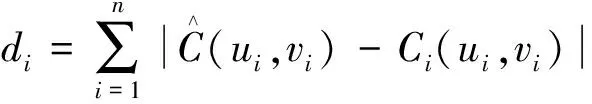
(3)
选取全球水平辐照度(global horizontal irradiance,GHI)、阵列平面辐照度(plane-of-array irradiance,POA)、直接法向辐照度(direct normal irradiance,DNI)、风向(wind direction,WD)、风速(wind speed,WS)、温度(temperature,T)、湿度(humidity,H)、降雨量(rainfall,RFL)作为特征变量。欧式距离计算结果如表1所示。
由表1可知,GHI、POA、DNI、WS这4个特征选取Gumbel-Copula函数作为最优Copula函数;WD、T、H、RFL这4个特征选取Frank-Copula函数作为最优Copula函数。上述特征的最优Copula函数导出的Spearman相关系数如表2所示。
由表2可知,三种不同角度的辐照度与光伏输出功率的相关性强,相关系数均大于0.89。风速、温度与光伏输出功率之间的相关性也较强,相关系数均大于0.65。风向、湿度与光伏输出功率之间呈现较强的负相关性,相关系数均大于0.49。

表1 欧氏距离计算结果Table 1 Calculation results of euclidean distance
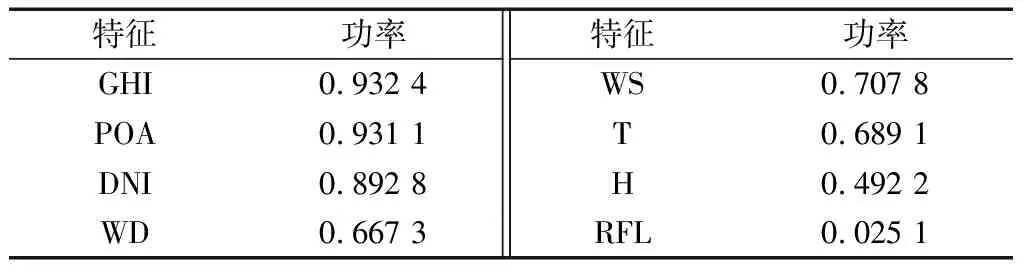
表2 Copula-Spearman相关系数表Table 2 Copula-Spearman correlation coefficient table
1.3 基于轻量级梯度提升机的特征贡献度分析
轻量级梯度提升机(light gradient boosting machine,LightGBM)是一种改进的梯度提升树(gradient boosting decision tree,GBDT)[13]。提出了梯度单边采样(gradient one-side sampling, GOSS)和独家特征捆绑(exclusive feature bundling,EFB)使得其相较于其他梯度提升树算法更高效。
LightGBM在训练的时候,将梯度较大的样本保留下来,梯度较小的采取随机抽样,并引入常量系数,对于训练集(x1,x2,…,xn)在每轮迭代的损失函数的梯度对应为(g1,g2,…,gn)[14]。
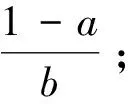
选取进行特征贡献度计算的特征向量表达式为
W=[GHI,POA,DNI,WD,WS,T,H,RFL]
(4)
由于各特征变量之间的单位不同,因此有必要对训练样本数据进行标准化处理,将各特征变量的数值转化为0~1,标准化的计算公式为
(5)
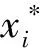
基于澳大利亚沙漠光伏站2019年7月1日至2021年1月1日的数据,LIghtGBM计算得到特征贡献度如图1所示。
图1可知,不同特征的贡献度存在差异,各特征贡献度分别为[230,35,103,121,73,84,149,15]。如果将判断标准设为30,并且将贡献度大于30的影响因素作为预测模型的输入,则可以剔除降雨量特征,但由于选取数据处于沙漠地区,全年降雨量较少,但光伏功率受到雨天的影响程度较大,因此保留降雨量特征。根据Copula相关性分析可知,三种不同角度的辐照度之间存在线性相关性,并均大于0.95属于强相关,且互相之间可以相互转化,所以仅保留全球水平辐照度作为输入变量。因此,根据Copula函数的相关性分析及LightGBM的特征贡献度计算,选取6个影响因素,与历史光伏输出功率数据作为模型的输入变量,具体如图2所示。
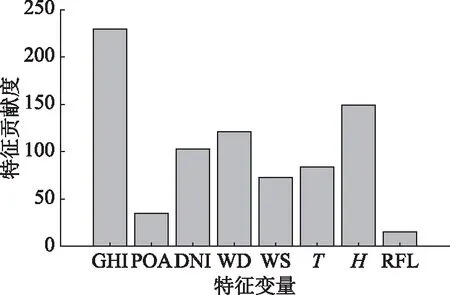
图1 特征贡献度Fig.1 Feature contribution

图2 输入变量图Fig.2 Input variable diagram
2 Stacking集成学习模型
2.1 Stacking理论
Stacking 集成学习算法通过将各类机器学习算法通过分层的形式融合起来[15]。首先,对原始数据重新划分,并输入至多个基学习器进行训练;然后,把多个基学习器的输出作为元学习器的输入,并训练得到最终结果。Stacking集成学习算法通过结合多个学习器的学习能力,使模型的准确性大幅度提高。Stacking集成学习算法框架如图3所示。

图3 Stacking集成学习框架图Fig.3 Stacking ensemble learning framework
2.2 极限梯度提升算法
极限梯度提升算法(extreme gradient boosting,XGBoost)由陈天奇博士提出,是一种强大的基于树的集成学习模型[16]。它使用分类回归树(classification and regression tree,CART)作为其弱学习者。在每次迭代中,残差将被用来修改之前的弱学习者。整个过程可视为CART的集成模型,XGBoost预测值的计算公式为
(6)
XGBoost目标函数的计算公式为
(7)
式(7)中:
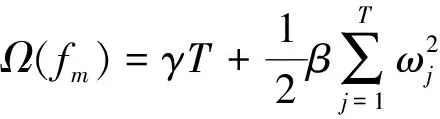
(8)
式中:n为样本数;l为二阶导数的损失函数,即训练误差;yxi为第i个样本的实际值;Ω(fm)为正则项;T为树中叶子节点的数量;ωj为叶子分数;γ和β为控制树的复杂度的参数。实际上,目标函数的优化就是确定CART树的结构和ωj的值。通过二阶泰勒展开,可以将目标函数简化为关于ωj的一元二次方程,目标函数展开的计算公式为

(9)
式(9)中:Ij为在叶子节点j中所有数据样本;gi和hi分别为损失函数的一阶和二阶导数。
2.3 基于Stacking集成学习的短期光伏功率预测模型
Stacking集成学习算法,通过将不同的机器学习算法融合在一起,并通过K折交叉验证来进行基学习器训练集的划分,再将基学习器训练后得到的结果作为元学习器的输入,从而得到最终预测结果。在Stacking集成学习模型的第一层除了选取梯度提升决策树(gradient boosted decision tree,GBDT)、XGBoost、LightGBM为主的Boosting模型,还选取以随机森林(random forest,RF)为代表的Bagging模型,再加入K最近邻算法(K-nearest neighbor,KNN)。在第一层分别选取多个不同类型的算法,这是由于不同类型的算法能让模型从不同数据空间和结构去训练数据,从而充分发挥不同算法的优势,使得预测性能达到最佳。在第二层的元学习器选取中,要考虑防止过拟合现象的出现,因此选取LightGBM算法这种泛化能力好的模型。综上所示,第一层基学习器为GBDT、XGBoost、LightGBM、RF、KNN;第二层元学习器为LightGBM。对于其中各个模型的超参数采用贝叶斯优化算法进行寻优[17],再定义一个超级学习器,采用5折交叉验证,并将基学习器和元学习器封装到超级学习器中训练。模型预测流程图如图4所示。
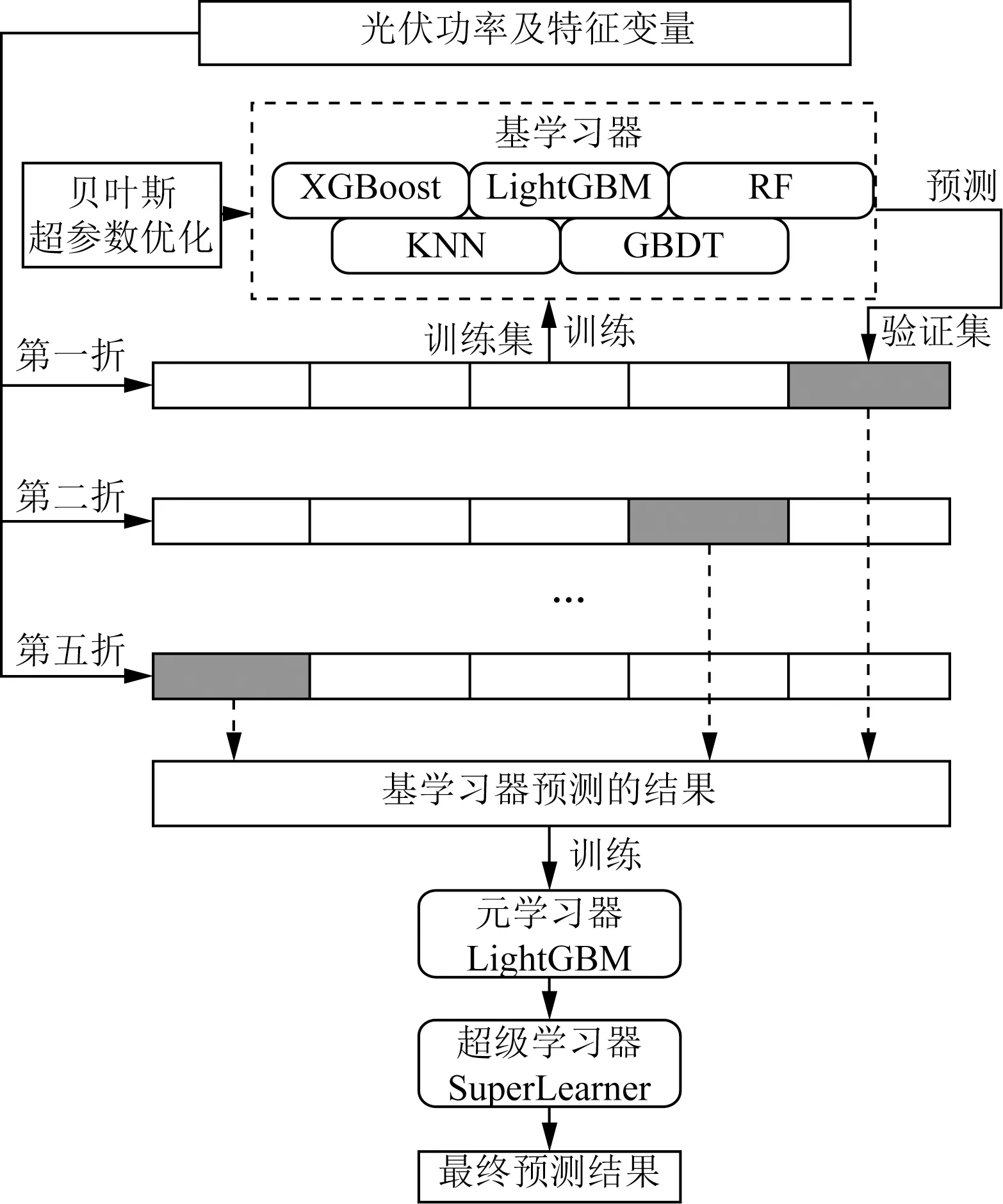
图4 Stacking集成学习预测流程图Fig.4 Flow chart of Stacking ensemble learning prediction
3 算例分析
采用澳大利亚沙漠太阳能中心(the desert knowledge australia solar centre,DKASC)的艾丽丝泉的光伏数据和天气数据,DKASC是澳大利亚中部地区商业太阳能技术的示范设施,选取2019年7月1日至2021年1月1日每天7:00—17:00的数据,采样间隔为1 h。采用的硬件设施为Inter Core i5-9300H、NVDIA GTX1660Ti 6G GDDR6独立显卡,软件平台为Python3.7.1和MATLAB R2016a。定义的超级学习器来自Python中的mlens库。
3.1 数据预处理
(1)考虑到在实际光伏数据记录过程中,人工的失误导致某一时刻数据出现异常情况,因此采用3σ准则[18]来进行异常值检测,并采用向前填补法来进行异常值替换。
(2)由于输入变量特征存在量纲不同的问题,因此对输入变量采用标准化处理,标准化的表达式如式(5)所示。
3.2 评价指标
采用平方绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE)来评估预测误差,用决定系数(R-square,R2)来评估模型的预测精度。各评估指标的计算公式为

(10)
(11)
(12)
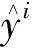
3.3 超参数选取
超参数的选取直接影响到最终Stacking模型的预测精度,因此采用贝叶斯优化算法来对基学习器模型进行超参数寻优,采用的是基于Python机器学习库中的Bayes-opt模块来进行调参。超参数选取结果如表3所示。
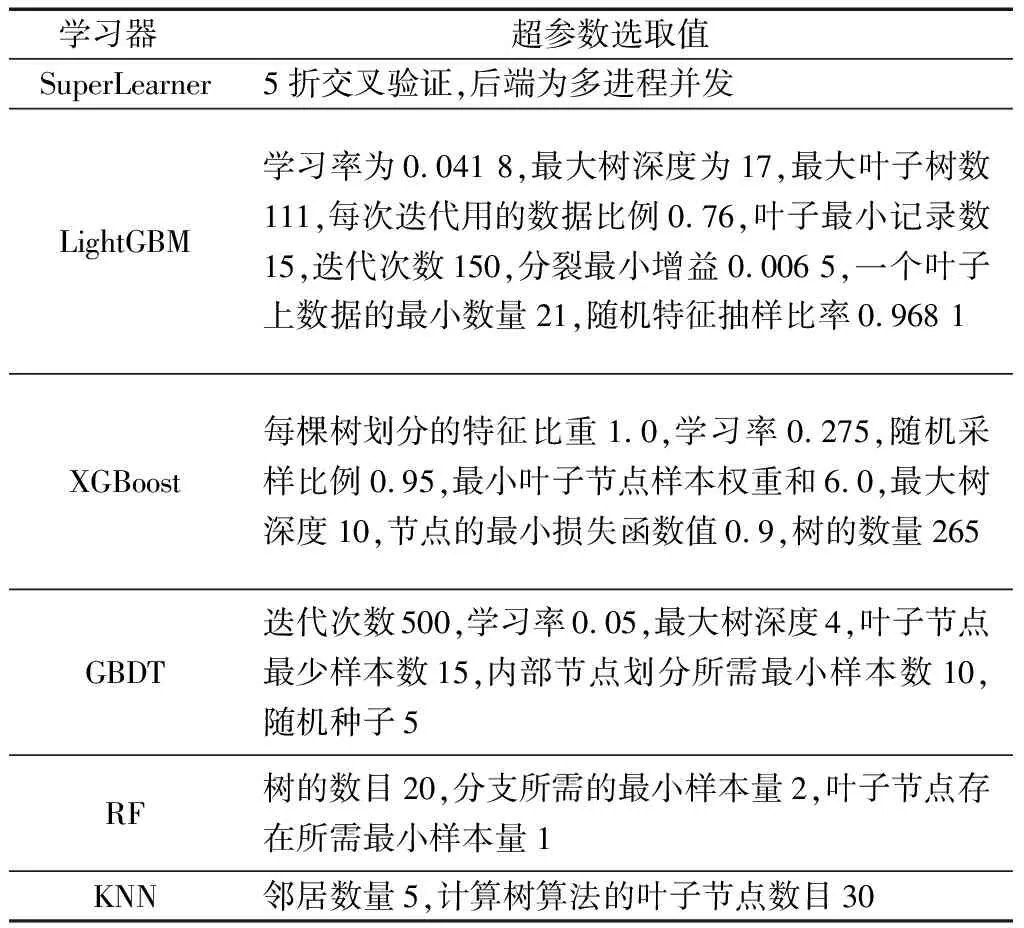
表3 学习器的超参数选取表Table 3 Hyperparameter selection table of learner
3.4 Stacking模型关联度及预测结果分析
为了验证本文模型组合能使得Stacking算法性能达到最优效果,所以对各个基学习器算法之间进行关联度计算。模型之间相关系数越大,表明模型融合的效果越好,预测的精度越高。各模型相关系数表如表4所示。
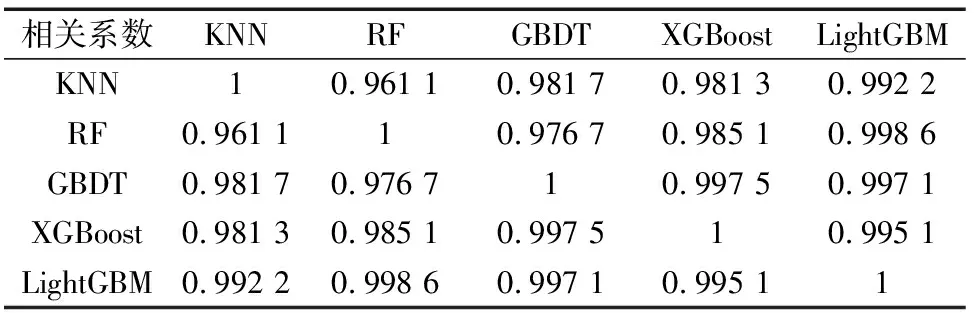
表4 各模型相关系数表Table 4 Correlation coefficient of each model
由表4中可知,本文所选取的各个模型之间的相关系数均超过0.95,具有非常强的相关性,表示将上述5个模型进行融合的预测效果较好。
为了进一步验证不同基学习器的选取对于模型预测结果的影响,对于基学习器进行随机选取,元学习器保持不变,不同基学习器组合下的Stacking模型预测误差结果如表5所示。
由表5可知,本文所选取的基学习器的MAE和RMSE误差值均为最小,R2最高,这是因为多样化的选取基学习器对于集成学习的效果越好,模型预测精度越高。
为了验证本文提出的基于贝叶斯算法的超参数优化方法有着更高的预测精度,因此,选取随机搜索算法,和网格搜索算法进行对比分析,对比结果如表6所示。

表5 不同基学习器组合的Stacking模型预测结果评价表Table 5 Prediction error evaluation table of Stacking model with different combination of base learners
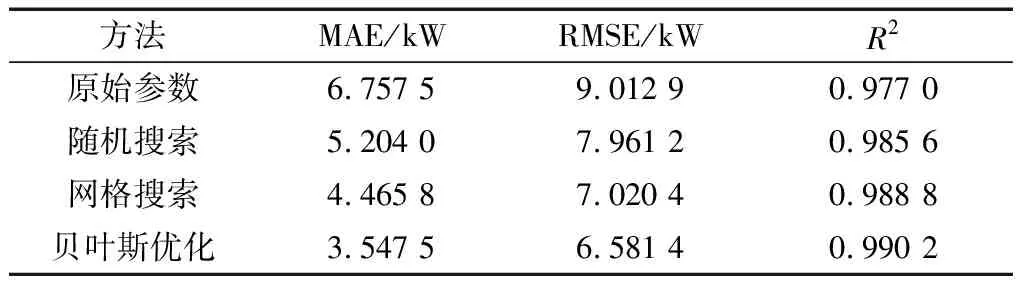
表6 不同优化算法预测结果对比Table 6 Comparison of prediction results of different optimization algorithms
由表6可知,本文提出的贝叶斯超参数优化方法相较于其他优化算法的MAE值和RMSE值误差最小,R2预测精度最高,这是由于贝叶斯优化算法在寻优时,会充分考虑之前参数的信息,不断更新先验,而随机搜索算法和网格搜索算法会忽视之前的信息,从而错过最优参数。
为了验证本文提出的模型在应对不同季节时的预测效果,因此在4个季节各选取一天来分别进行对比分析。春季选取的是2020年3月12日;夏季选取的是2019年8月15日;秋季选取的是2020年11月21日;冬季选取的是2020年12月31日,预测结果对比图及预测结果评价表如图5和表7所示。
由图5可知,在不同季节情况下,光伏输出功率都呈现出先升高后降低的变化趋势,在10~13 h时光伏输出功率值最大,这是由于该时间段的太阳辐射度最大,导致光伏输出功率增大。秋季的光伏输出功率曲线相较于其他三季呈现较为明显的波动趋势,这是由于秋季天气较为复杂,且温差较大,导致光伏输出功率波动较大。
由表7可知,在不同季节下,本文所提出的模型的误差值最小,预测精度最高。春季的预测精度比冬季提升了2.48%,这是由于春季的气象变化较为平稳,光伏输出功率受到天气影响较少,因此误差较低。夏季的预测精度最高,这是由于夏季温度较高,同时太阳辐照量充足。秋季的预测精度相较于春季和夏季明显降低,这是由于秋季天气较为复杂,太阳辐射减少,且昼夜温差较大,导致了预测精度下降。冬季的预测精度最低,这是由于冬季温度偏低,雨雪天气变多,导致了预测精度偏低。

图5 四季输出功率对比图Fig.5 Comparison of power output in four seasons
为了验证本文所提出的模型在应对不同天气类型时的预测精度,分别在晴天和雨天场景下,来进行对比分析,预测结果如表8所示。
由表8可知,在各个模型预测结果下,雨天的预测误差较高,预测精度较低,这是由于雨天的云层的剧烈变化加剧了天气的随机性,导致了光伏出力的不稳定。
在不同季节和不同天气场景下,本文所提出的模型均获得了更高的预测精度,这是由于本文将多个集成学习算法融合在Stacking框架下,使得模型能够从不同空间去深度挖掘数据间的关系,从而提高模型的稳定性和泛化性。

表7 不同季节的预测结果评价表Table 7 Evaluation table of prediction results in different seasons
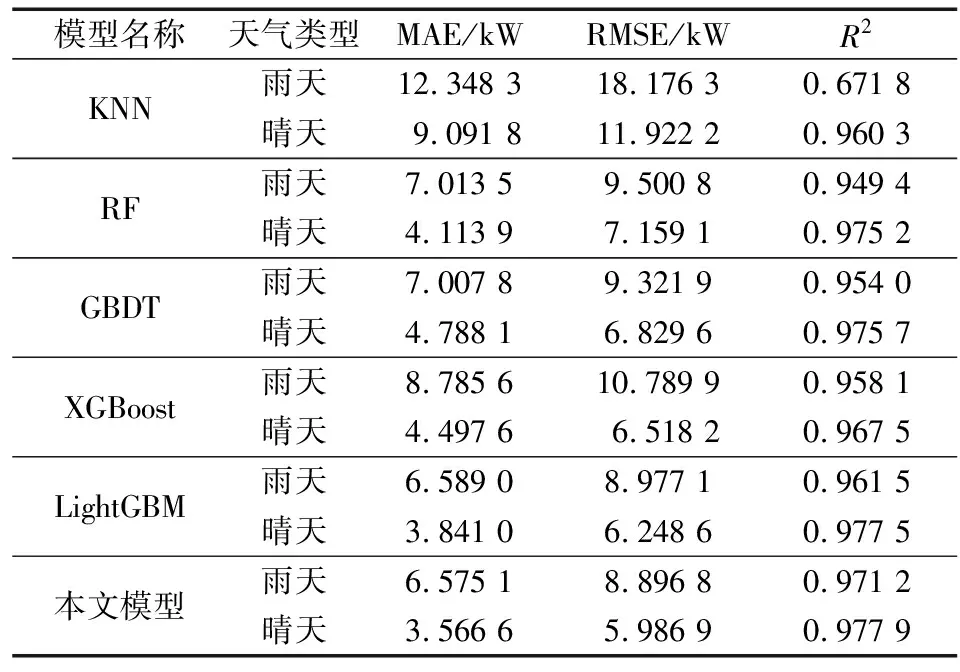
表8 晴天与雨天预测结果评价表Table 8 Error index of sunny and rainy days
4 结论
提出了一种在Stacking集成学习框架下融合Bagging和Boosting算法的短期光伏功率预测模型,引入Copula函数来进行相关系分析,以及LightGBM的特征贡献度计算进行特征筛选,并将模型封装至超级学习器中进行预测,得到如下结论。
(1)相较于其他Stacking模型组合和各单一模型,本文提出的模型组合的误差值最小,预测精度最高。
(2)本文提出的贝叶斯超参数优化算法,相较于其他优化算法误差值更低,预测精度更高。
(3)季节变化对于模型的预测精度影响较大,冬季的预测精度最低,夏季的预测精度最高, 夏季的值相较于冬季R2提高了2.63%。
(4)天气类型对于模型的预测精度影响较大,雨天的预测精度低于晴天。在两种不同天气类型下,本文提出的模型在晴天和雨天的R2之差最小,只有0.69%,表明模型的稳定性最好。
