并联管线复杂连接阀组的水锤边界条件求解方法

党云刚，周龙才，邓云龙

（1.陕西省水利电力勘测设计研究院，西安 710001；2.武汉大学水利水电学院，武汉 430072）

0 引 言

为缓解水资源时空分布不均，实现水资源合理配置，近年来我国兴建了一批大型调水工程［1］。采用重力流管道输水的长距离大流量调水工程一般设并联的双管线，以保障供水的可靠性。扩大单元的并联双管线需要在管线间设置连接阀来实现配水或检修时切断或恢复部分管段的输水。当输水管径较大时，为减少关阀末期阀门开度的变化梯度，从而减小关阀水锤压力，有的输水工程检修阀或调流阀设有旁通管，并在旁通管上安装旁通阀［2，3］。设置旁通管或旁通阀对减小水锤压力波动较好效果［4-6］，如果并联双管线的连接阀组也采取主阀加旁通管的形式，则构成复杂连接阀组，形成复杂的水锤计算边界条件。

复杂连接阀组在工程中较为少见，关于其边界条件求解方法的研究也很少见到。即使有的工程设置了复杂连接阀组，但在水锤计算中为了避免求解复杂连接阀组的非线性方程组，也可通过改变阀间的连接管长度或波速，在连接管上设置若干计算节点，从而将阀组分解成多个单独阀或带旁通阀的阀组。这种改变管段长度或波速的方法在工程应用中是可以满足计算精度要求的［7］，但从水锤计算的研究及发展的角度来看，则有必要研究分析复杂连接阀组的水锤边界条件求解方法，以完善水锤计算理论，为准确进行长距离大流量并联管线调水工程的水锤计算提供技术支持。

1 数学模型

输水管道中的瞬变流的基本微分方程为双曲型，目前工程中应用最多的求解方法是一维特征线法［8］。下面基于特征线法来分析阀门边界条件的求解。

1.1 管路中的单独阀边界条件

对如图1 所示的管路中的单个阀，采用特征线法时其边界条件如下［9］：

图1 管路中的单个阀Fig.1 Single valve in pipeline

式中：QX为通过阀门的流量；HX，1、HX，2为阀前、后的压力水头；CP、CM为水锤相容性特征线方程中的计算常数；B1、B2为管道特性常数；CX= τ2μ2A2g 定义为阀系数；A 为阀门全开时的过流面积；τ为阀门无量纲开度系数；μ为阀门全开出流系数（与全开时的阻力参数ξ有关）。

解方程组（1）得到通过阀的流量QX为：

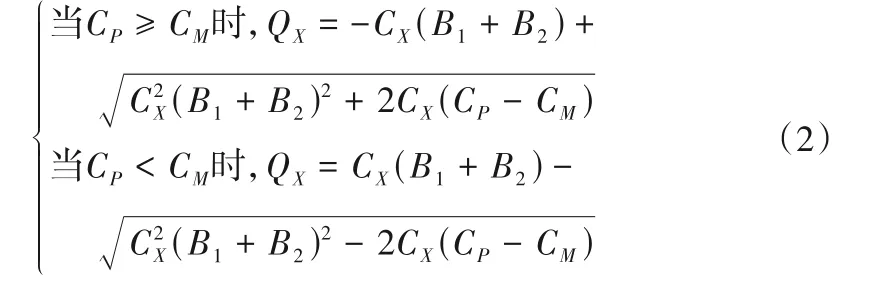
求得QX后，按式（1）的前两式可进一步求得阀前后的压力水头HX，1、HX，2，限于篇幅，后面不再说明其他变量的求解。

1.2 管路中的串联阀组边界条件

对如图2 所示的管道中n 个阀串联的阀组，采用特征线法时其边界条件为：

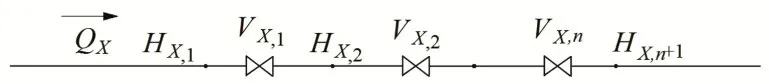
图2 管路中的串联阀组Fig.2 Series valves in pipeline

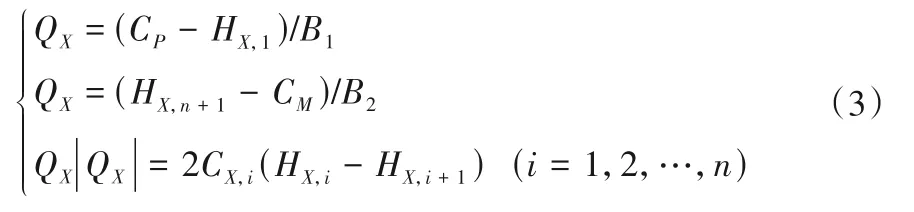
式中：QX为通过各阀门的流量；HX，i、HX，i+1为第i个阀前、后的压力水头为第（ii=1，2，…，n）阀的系数。

由式（3）的第3式，可得：

1.3 管路中的并联阀组边界条件

对如图3 所示的管道中n 个阀并联的阀组，设通过阀组的总流量为QX，则其边界条件为：

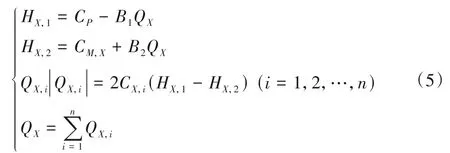
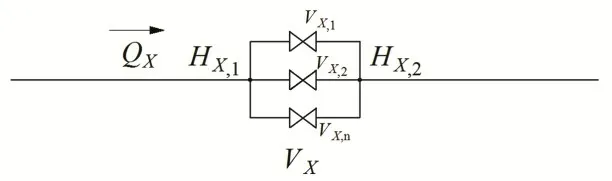
图3 管路中的并联阀组Fig.3 Parallel valves in pipeline

因为并联阀组内不会产生环流，故各阀内流量方向相同，由式（5）的后两式可得：

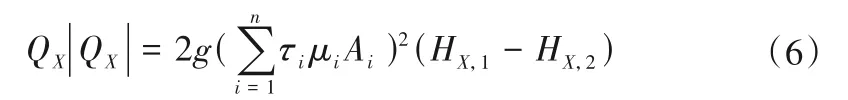
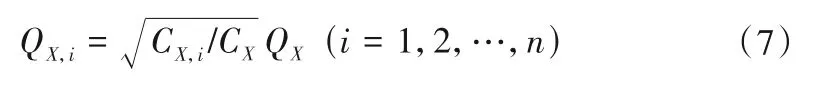
1.4 复杂连接阀组边界条件

设输水的并联管线分别为L1、L2，两管间有连接阀VV，连接阀前后分别均有检修阀（VⅠ、VⅡ、VⅢ、VⅣ）；考虑到模型通用性，假设连接阀、检修阀均是由并联的阀组构成，并联阀最多为n个，如图4所示。当各阀组间的连接管较长时，图4中HA与HI，2、HII，1、HV，1之间，HB与HIII，2、HIV，1、HV，2之间存在至少1 个管段计算节点，则各阀组被这些计算节点隔开，成单独的并联阀组，其水锤边界条件求解方法如前所述。

图4 并联管线的复杂连接阀组Fig.4 Complex connecting valve group of parallel pipeline

当各阀组间的连接管较短时，则图4 中近似有HA=HI，2=HII，1=HV，1，HB=HIII，2=HIV，1=HV，2，这样各阀组的边界条件耦合而成复杂的非线性方程组，求解较麻烦。为避免求解复杂连接阀组的非线性方程组，或者直接应用商用软件，工程计算中可采用人为加大连接管段长度，或减小连接管段水锤波速的方法，从而在连接管上增加计算节点，将复杂连接阀组的各阀组概化为管路中间阀。这种方法从工程应用的角度是可行的，但毕竟是近似的方法，同时也增加了建模工作量。

在此，分析连接管较短情况下的复杂连接阀组的水锤边界条件求解方法。将并联阀组简化为单独阀（按并联的阀组计算则图4 的并联管线复杂连接阀组可以简化为如图5的布置形式。

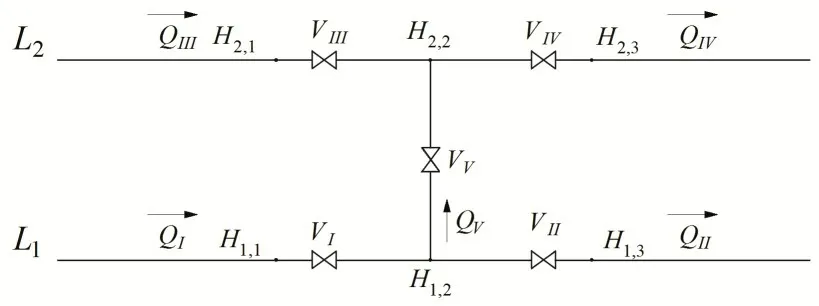
图5 复杂连接阀组简化图Fig.5 Simplified diagram of complex connecting valve group

采用特征线法求解时，有如下的边界条件：

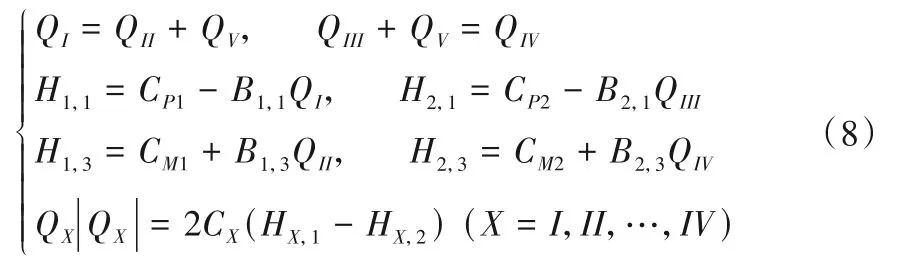
式中：CP1、CP2及B1，1、B2，1分别为阀VⅠ、VⅢ左侧的水锤相容性特征线方程中的计算常数及管道特性常数；CM1、CM2及B1，3、B2，3分别阀VⅡ、VⅣ右侧的水锤相容性特征线方程中的计算常数及管道特性常数；X 为阀组编号；HX，1、HX，2为阀组两侧压力水头，对应于H1，1～H2，3等。

式（8）形成复杂的方程组，可采用如下方法来求解：

（1）当任有3个及以上的阀组关闭时，则通过各阀组的流量均为0。

（2）当中间连接阀组关闭，即CV=0 时，QV=0，按VⅠ、VⅡ两个阀组串联计算QI= QV，按VⅢ、VⅣ两个阀组串联来计算QIII= QIV。

（3）当同管线两个检修阀组关闭，比如CI=0、CII=0 时，则QI= QII= QV= 0，按VⅢ、VⅣ两个阀组串联来计算QIII= QIV。

（4）当非同管线的两个检修阀组关闭，比如CI=0、CIV=0 时，则QI= QIV= 0，按VⅡ、VV、VⅢ三个阀组串联来计算QII= -QV=QII。

（5）当只有一个检修阀组关闭，比如CIII=0 时，则QIII= 0，化简方程组（8）得：

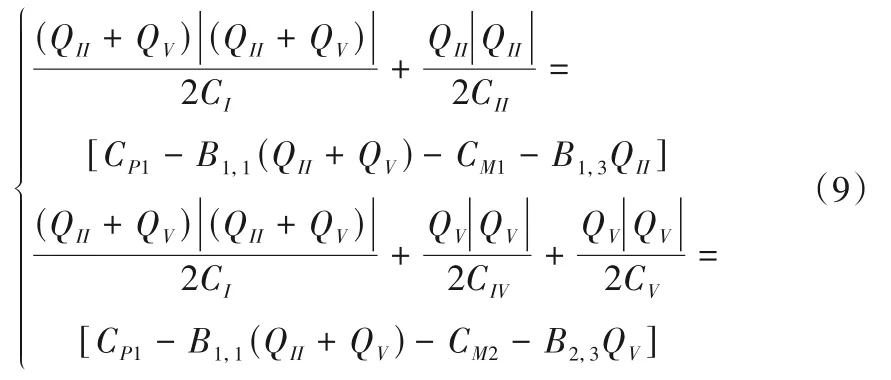
方程组（9）有2个方程，2个未知数QII、QV，可采用牛顿迭代法求解；进而可求得其他未知量。

（6）当检修阀组及连接阀组全部开启时，化简方程组（8）得：

方程组（10）有3个方程，3个未知数QII、QIII、QV，同样采用牛顿迭代法求解；进而可求得其他未知量。

2 实例计算

2.1 基本资料

陕西省内某大型调水工程的输水道中的一段自桩号0+715～桩号39+020 为重力流压力管道输水，全长38.31 km，设计流量为30～23 m3/s，采用两根DN3400管道布置。为便于管道分段检修，本段布置3 座连通阀井，分别在干线桩号11+100、17+847、28+000 处，连通井内设置DN3400 电动蝶阀，其中Ⅱ、Ⅳ阀设置带DN800半球阀的旁通管，如图6所示。正常运行时，连接阀井的Ⅴ阀处于关闭状态。

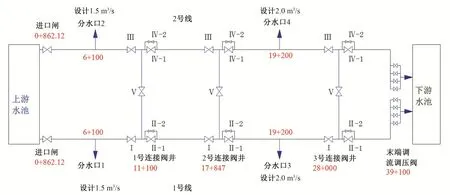
图6 某调水工程连通阀井布置Fig.6 Layout of connecting valve wells of a water transfer project

2.2 部分管段检修时的关阀水锤计算

设在设计流量（首端30 m3/s、末端23 m3/s、总分水7 m3/s）下运行时，需要检修1号管线的1号连接阀井与2号连接阀井之间管段，通过相应闸阀的操作切除这一管段运行，并且将分水流量减小到设计分水流量的70%。

经调算，设定相关阀门分水口及相应阀开关设置如表1 所示。其中分水口在180 s 内减小分流量到70%，连接阀在180 s打开。

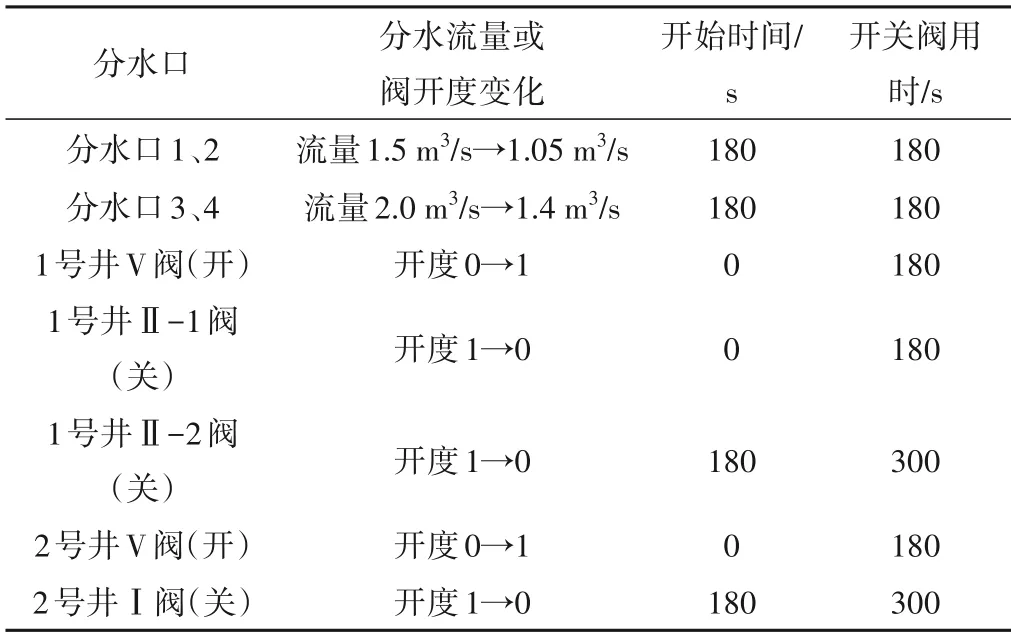
表1 分水口及相应阀的开关设置Tab.1 Opening and closing setting of water diversion port and corresponding valves

开发了带复杂连接阀组的重力流水锤开发了计算软件并应用于本工程的计算。针对本工况，计算得到的1 号连接阀井处的Ⅰ阀前、分汇流点A、Ⅱ阀组后、Ⅲ阀前、分汇流点B、Ⅳ阀组后等不同位置的压力变化过程线及通过Ⅰ～Ⅴ等各阀（组）的流量变化过程线如图7所示，不同的压力流量线按颜色标识。

图7 1号连接阀井处的压力、流量变化过程线Fig.7 Pressure and flow change process line at No.1 connecting valves well

在关闭1 号井Ⅱ-1 阀、Ⅱ-2 阀过程中，Ⅱ阀组后压力有明显的压力下降，Ⅱ阀组后压力由86.33 m 下降到71.3 m，降幅15.03 m。操作阀组来关闭部分管段过程中出现了压力波动，但计算得到各阀（组）的水力波动具有较好的连续性和一致性，没有出现因数值计算误差引起的异常，表明复杂连接阀组的水锤边界条件求解方法是准确的。

计算得到的1 号管线压力水头包络线如图8 所示，其中工作压力水线为关阀前正常运行的压力水头沿线分布线，最高、最低压力水线为关阀过程中出现的最高、最低压力沿程分布线。全线最大压力111.734 m、最低压力4.0 m；虽然在关闭1 号井Ⅱ阀组过程中，Ⅱ阀组后压力有明显的压力下降，但压力下降仍在合理的范围内。

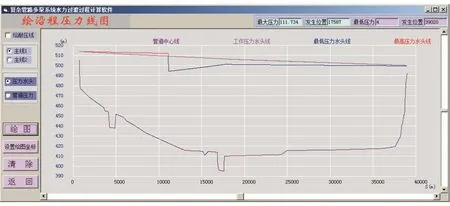
图8 1号管线压力水头包络线Fig.8 Pressure head envelope of 1#pipeline

2.3 取消旁通阀的对比计算

为进行对比分析，现取消1 号连接阀井Ⅱ阀组的DN800 旁通阀，其DN3400 的主阀不变。针对前述检修工况，设1 号连接阀井的Ⅱ阀在480 s内关闭，其余计算条件同前。

计算得到的1 号连接阀井处压力、流量变化过程线如图9所示。在关闭1号井Ⅱ阀过程中，Ⅱ阀组后压力由86.33 m下降到60.7 m，降幅25.63 m，比设旁通阀情况下降10.6 m。相对设旁通阀，不设旁通阀关闭部分管段过程中出现了更剧烈的压力波动。

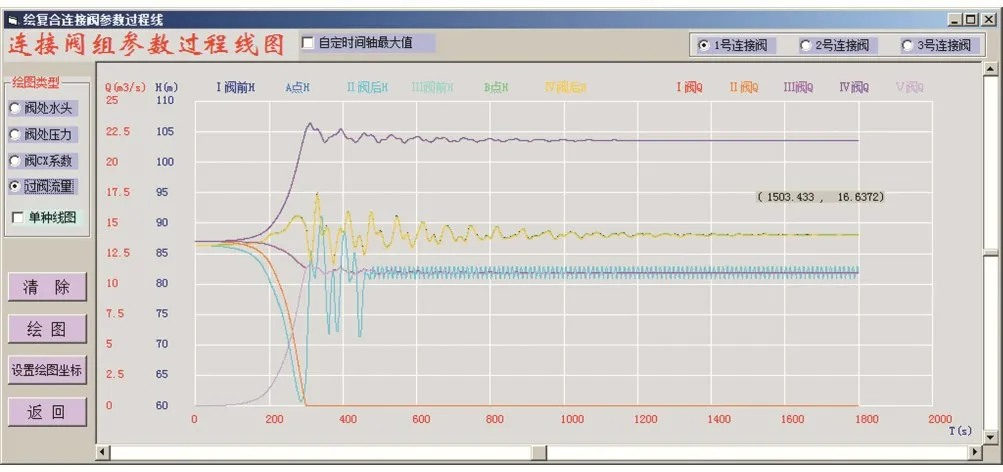
图9 1号连接阀井处的压力、流量变化过程线（无旁通阀）Fig.9 Pressure and flow change process line at No.1 connecting valves well（without bypass valve）

计算得到的1 号管线压力水头包络线如图10 所示，全线最大压力119.104 m、最低压力4.0 m；在1 号连接阀井Ⅱ阀后有明显的压力下降更为明显。因此，虽然Ⅱ阀组设置旁通阀增加了工程投资，但有利于减小关阀时压力波动。

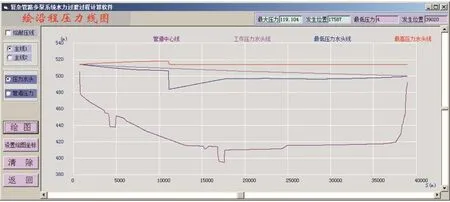
图10 1号管线压力水头包络线（无旁通阀）Fig.10 Pressure head envelope of 1#pipeline（without bypass valve）

3 结 论

（2）针对长距离大流量并联管线的复杂连接阀组，推导了多并联阀（含旁通阀）组合的并联管线连接阀组边界条件的通用方程组并进行简化，给出了最终得到的非线性方程组的数值求解方法。对某调水工程的进行了检修时关闭部分管段的水力过渡过程计算，计算得的压力波动具有较好的连续性和一致性，没有出现因数值计算误差引起的异常，表明复杂连接阀组的水锤边界条件求解方法是准确的。

（3）对某调水工程中的1 号连接阀井II 阀组是否设置旁通阀进行了对比计算。结果表明，设置旁通阀时，按先主阀180s关闭、再旁通阀300 s 关闭，则1 号连接阀井II 阀组后压力由86.33 m 下降到71.3 m，降幅15.03 m；取消旁通阀后，按主阀480 s 关闭，则1 号连接阀井II 阀后压力水头由86.33 m 下降到60.7 m，降幅25.63 m，比设旁通阀情况下降10.6 m。而且不设旁通阀关闭部分管段过程中出现了更剧烈的压力波动。因此，设置旁通阀有利于减小关阀时压力波动。