双工字钢-混组合连续弯梁桥有效宽度
2022-02-17江林松徐略勤熊光泽陈叙先
江林松, 徐略勤,2*, 熊光泽, 陈叙先
(1.重庆交通大学土木工程学院, 重庆 400074; 2.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室, 重庆 400074)
钢-混凝土组合梁近几年在中国得到了空前的发展,由于其经济性良好、施工方便、受力合理等优点,被广泛应用于公路和城市桥梁中。钢-混凝土组合梁桥可以充分挖掘并利用传统混凝土和钢材的材料性能潜力,也符合中国绿色交通、标准化和工业化建造的发展趋势[1]。随着工程实践的不断推进,钢-混凝土组合梁逐渐开始应用于平面弯桥之中。弯梁桥本身存在强烈的弯-扭耦合效应,而钢-混组合弯梁桥的混凝土桥面板还存在明显的剪力滞效应,两种效应的叠加使得混凝土桥面板的应力状态更为复杂。为了便于工程应用分析,中外规范[2-3]与国外规范[4-7]通常采用有效宽度来简化处理混凝土桥面板的剪力滞效应。有效宽度的取值影响着组合梁挠度验算和剪力钉设计的合理性,尤其对组合梁正常使用阶段的变形验算有很大影响[8],因此是组合梁桥设计计算的重要考量之一。
从各国规范[2-7]的规定来看,影响组合梁混凝土桥面板有效宽度的主要因素有:梁跨与桥面板宽度之比L/b、荷载类型及其沿梁跨方向的位置、桥面板厚度、抗剪连接程度以及混凝土桥面板和钢梁的刚度比等。为了便于应用,各国规范一般选取其中几项因素来决定有效宽度的取值,但由于影响因素较多,影响机理较复杂,钢-混凝土组合梁桥面板有效宽度的合理取值一直都是中外学者的研究重点之一。刘寒冰等[9]利用能量变分法,探讨了不同荷载作用下翼缘板有效宽度的变化情况;聂建国等[10]用荷载类型与宽跨比作为参数进行组合,提出了具有很高精度的翼板有效宽度简化计算公式;文献[11-13]基于几何构造对组合梁的翼缘有效宽度进行了不同类型的参数分析。但已有研究主要针对的是正交直桥,对于平面弯桥的研究则非常欠缺。文献[14-17]提出曲线组合箱梁的理论模型,研究了不同截面形式的曲线梁的剪力滞效应;张庆[18]还详细探讨了跨曲比对剪力滞效应的影响并提出了设计建议,但都没有进一步探讨桥面板的有效宽度问题。随着钢-混组合梁在平面弯桥中的进一步推广使用,桥面板有效宽度的合理取值问题会更加突显。
因此,基于某在建实际工程,现针对其所采用的双工字钢-混组合连续弯梁的结构特点,结合中外相关设计规范,研究了混凝土桥面板有效宽度的取值问题,对影响桥面板有效宽度的关键因素进行了参数分析,最终提出双工字钢-混组合连续弯梁桥混凝土桥面板有效宽度的简化计算方法,以期为同类结构提供参考。
1 研究背景
剪力滞效应使得组合梁混凝土桥面板内的实际正应力分布呈现如图1所示的不均匀状态。在线弹性分析中,通常假定在桥面板的一定范围内,弯曲正应力均匀分布,这一范围就称为有效宽度beff。将桥面板实际非均匀分布的最大正应力作为有效宽度内的应力值,然后根据合力相等原则(图1中面积ABCDE与HIJK相等)求得有效宽度beff。
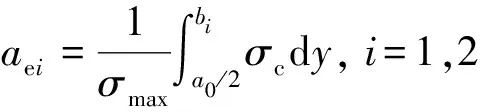
(1)
式(1)中:aei为无剪力键区域的单侧混凝土板有效宽度;a0为剪力键的外侧中心距;bi为单侧混凝土桥面板的实际宽度;σmax和σc分别为桥面板内最大正应力和分布正应力。混凝土桥面板的有效宽度beff可写为
beff=be1+be2=ae1+a0+ae2
(2)
采用式(1)和式(2)来确定正交直桥桥面板的有效宽度相对比较成熟,但平面弯桥的弯扭耦合效应使得正应力σc的计算变得困难。本文以某在建桥梁所采用的双工字钢-混组合连续弯梁结构为例来展开研究。如图1所示,该桥为4 m×25 m连续组合梁结构,平面曲率半径为R=250 m,桥面全宽10.5 m,工字钢梁高1.3 m,采用Q345qD钢材,两片钢梁的标准间距为5.6 m;预制桥面板悬臂翼缘厚25 cm,根部厚41 cm,采用C40混凝土;钢梁与混凝土板间设置集束式Φ22 mm圆柱头焊钉。由于剪力
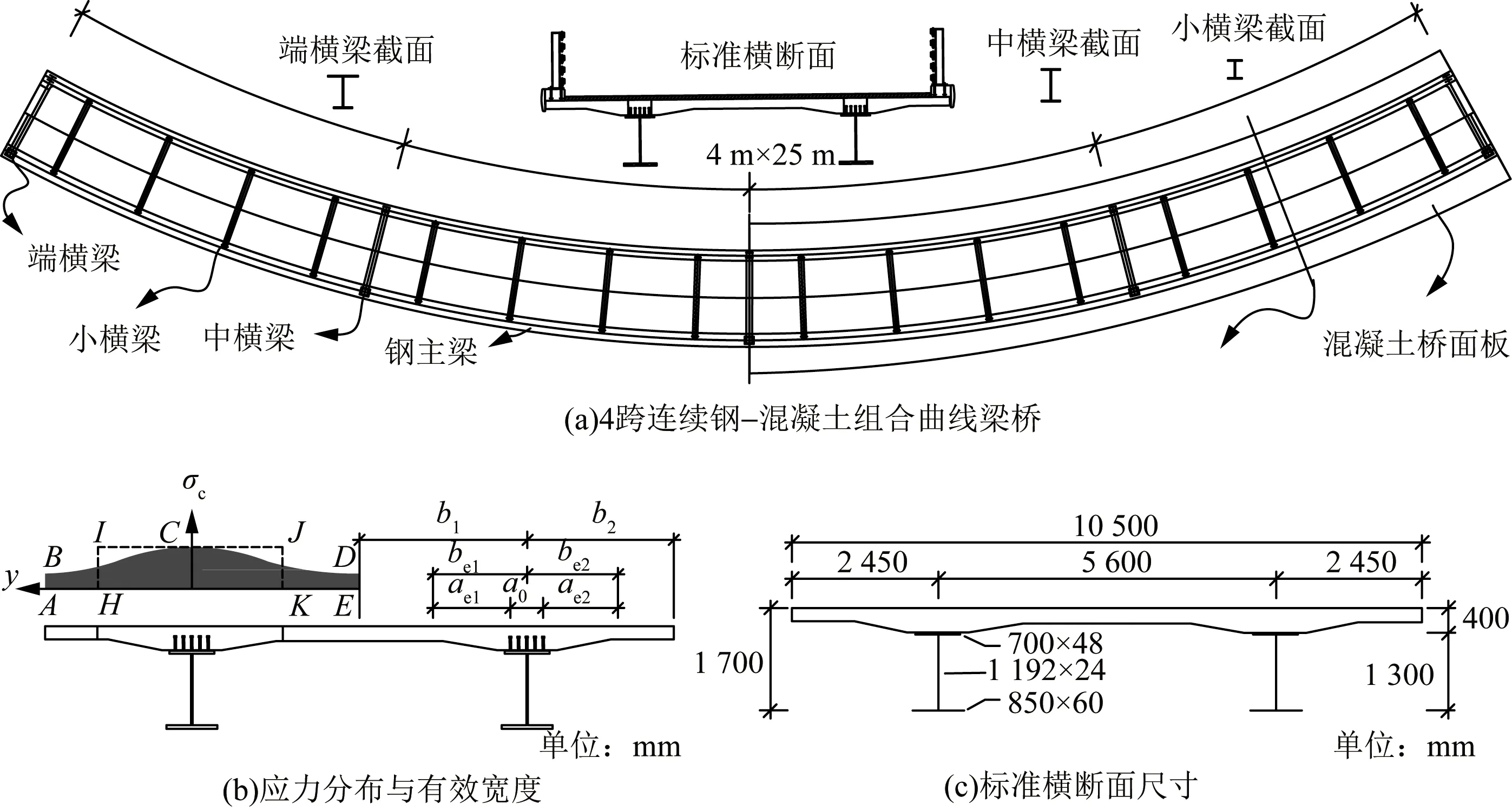
y为横桥向方向;bi为单侧桥面板实际板宽;bei为单侧翼缘有效宽度图1 桥面板有效宽度定义Fig.1 Definition of effective flange width
钉的存在,钢-混组合梁在受力时桥面板和钢梁间会产生界面滑移效应,但文献[8]认为,界面滑移主要影响组合梁的变形,对桥面板剪力滞效应的影响较小,这在文献[9-10]中得到进一步的验证。因此,提出如下假设。
(1)不考虑弹性工作状态下混凝土桥面板与钢梁的界面滑移。
(2)在桥宽范围内,混凝土桥面板中的正应力σc沿板厚方向分布规律相同。
(3)采用梁轴线的曲率半径来计算桥面板的应变,忽略曲率沿横桥向的变化。
2 连续组合梁有效宽度的基本规定
2.1 中外主要规范的规定
2.1.1 中国规范JTG/T D64-01和GB50017—2017
中国规范[2-3]均以桥面板宽和跨径作为主要因素,相对之前版本的规范进行了改进,不再考虑有效宽度和混凝土板厚的关系,因此更具经济性,但在某些宽跨比较小的组合梁中,按规范算出的有效宽度与实际板宽相同,存在高估的现象[8]。另外,相比JTG/T D64-01,GB50017—2017区分了有无板托的区别。同时,两部规范均对连续梁正、负弯矩区的不同受力性质进行了讨论。其中,JTG/T D64-01明确提出了等效跨径的概念及其取值。
2.1.2 美国规范AASHTO
美国规范AASHTO[4]规定,组合梁混凝土桥面板的有效宽度应满足:
(3)
式(3)中:leff为等效跨径;t为混凝土桥面板的平均厚度;a为取钢梁腹板厚度和钢梁上翼缘板宽一半的较大值;w1和w2分别为相邻钢梁平均中心距和混凝土悬臂翼缘宽度。
另外,对于连续组合梁桥,AASHTO按照均布荷载作用下的弯矩图,根据反弯点的距离确定每一部分的等效跨径。
2.1.3 欧洲规范EC4
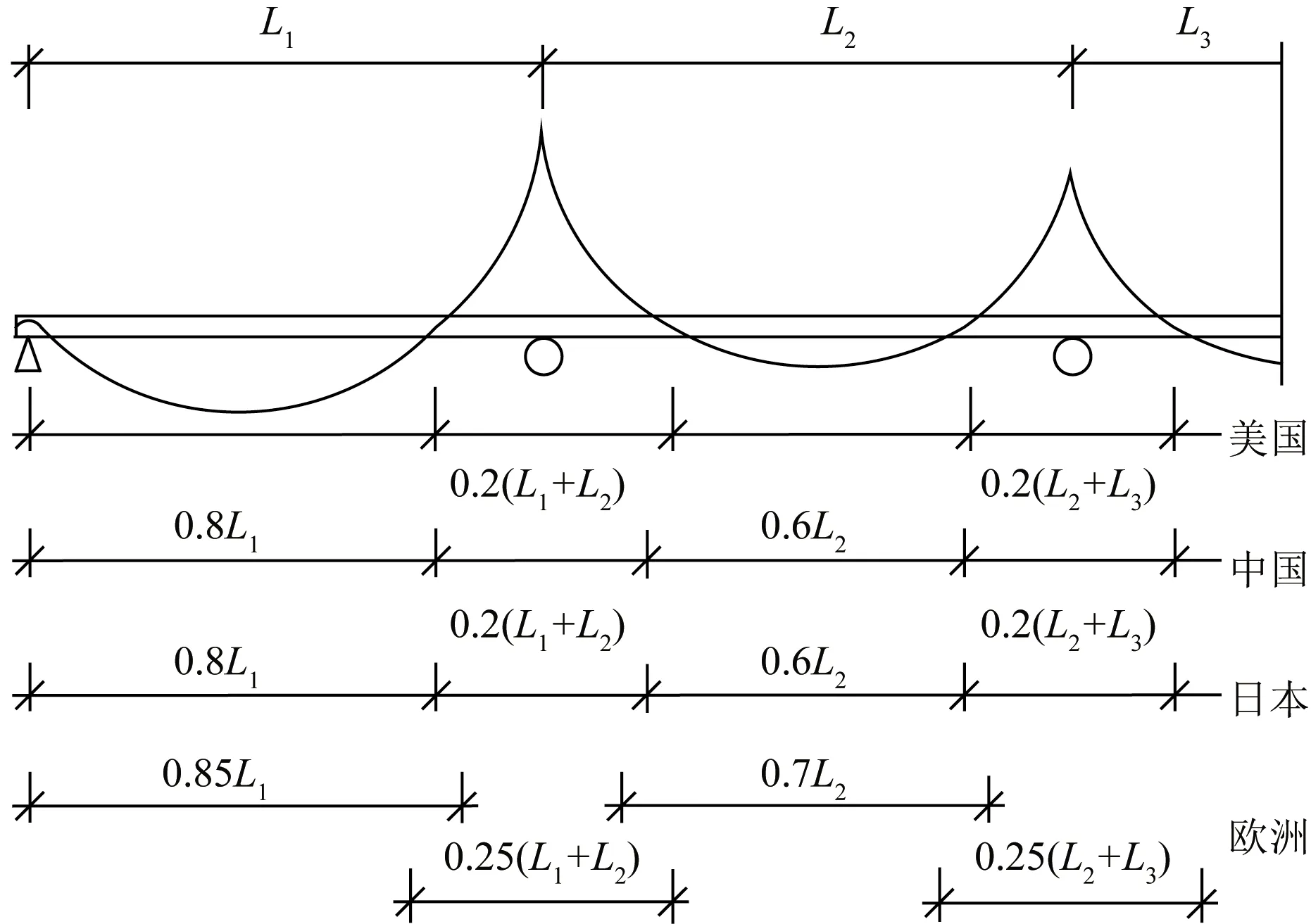
欧洲规范EC4[5]是中国规范JTG/T D64-01的主要参考对象,因此两者考虑的影响因素基本一致,只是在等效跨径leff的计算上存在差异,具体如图2所示。
2.1.4 日本规范JRA
日本规范JRA[6]对组合梁桥面板有效宽度的计算分为均布荷载和集中荷载两种情况。
均布荷载下:
(4)
集中荷载下:
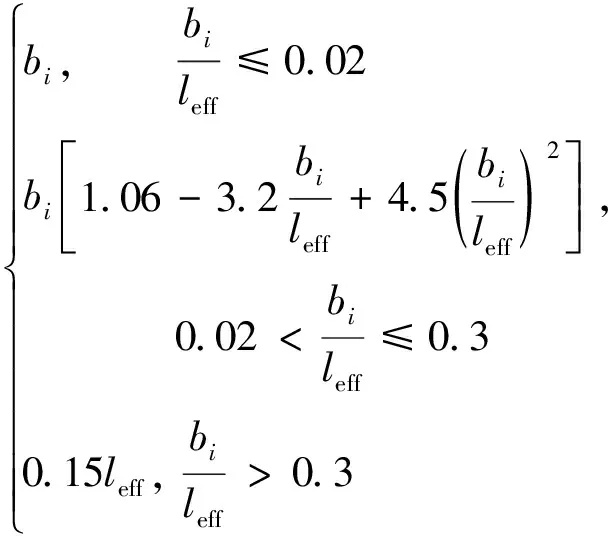
(5)
2.2 规范对比分析
根据上述规范的具体规定,表1列举了各规范的主要考虑因素及其基本特征。
由表1可见,各国规范在针对连续组合梁桥的有效宽度时,都分别考虑了正、负弯矩区。采用等效跨径leff这一概念,可将连续梁按照正、负弯矩的分布情况划分为多个简支梁,其中,中间支承处可视为方向向上的集中力。各国规范关于等效跨径的规定如图2所示,其中,美国规范按照连续梁在均布荷载下的弯矩图确定等效跨径,虽然准确但过程繁琐,不便于计算;中国和日本规范与连续梁的弯矩图较为吻合;欧洲规范中,边跨和中跨的等效跨径与支承处的等效跨径均存在重合部分。
各国规范通常都采用不同的比例系数来体现连续梁边跨与中跨的内力区别,在内、外支承处却很少做出区分。实际上,边跨和中跨、中跨和中跨之间的支承点是存在差异的,忽略这种差异容易造成计算结果不安全或者不经济。为进行直观对比,将第1节中的背景桥例直接改为正交直线桥,采用ABAQUS软件建立实体模型,如图3所示。混凝土桥面板与工字梁板梁之间采用绑定的方式连接,为保持与实际工程一致,参考原始桥例,在边支座处设置端横梁,中支座处设置中横梁,每跨另设置四道小横梁,主梁和横梁之间均采用绑定的方式连接。
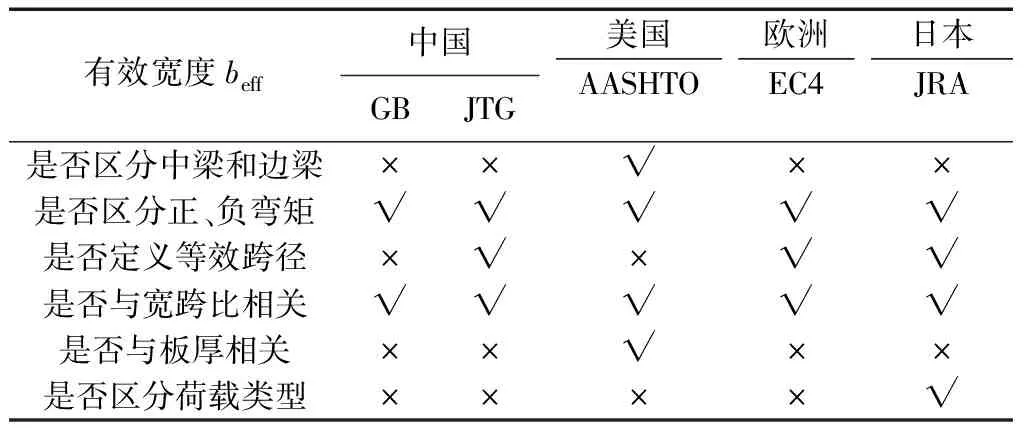
表1 各规范对有效宽度的规定Table 1 Requirements for effective flange width by design codes
L1~L3依次为连续梁第1~3跨图2 连续梁桥等效跨径的比较Fig.2 Comparison of effective span lengths of continuous bridge
各国规范(为便于说明,后文分别简称为JTG、GB、AASHTO、EC4和JRA)对连续组合梁混凝土桥面板有效宽度沿跨长的取值情况如图4所示,由于结构对称,图4中仅给出了两跨的结果。由图4可见,AASHTO因为将混凝土板厚作为有效宽度计算的影响因素,严重低估了除支座附近以外的有效宽度;由于宽跨比较小,GB、JTG和EC4的有效宽度在跨中部分取值为实际板宽,略微高估了连续组合梁的有效宽度。从数值来看,在边跨跨中处,JTG和EC4的取值均高出有限元结果2.70%;在中跨跨中处,JTG的取值高出有限元结果4.17%,EC4的取值比有限元结果低2.56%。中国规范JTG和GB取等效跨径的1/6作为有效宽度,EC4取等效跨径的1/8作为有效宽度,后者更为适用于小宽跨比连续组合梁有效宽度沿跨径方向的计算。JRA虽然不考虑混凝土板厚的影响,但是其边跨和中跨的跨中有效宽度取值分别比有限元结果低14.11%、21.13%,显然偏保守。其原因在于,日本规范尽管也将宽跨比作为主要因素来计算有效宽度,但只有当宽跨比小于0.05时才将实际板宽直接作为有效宽度,因此取值明显低于中国和欧洲规范。
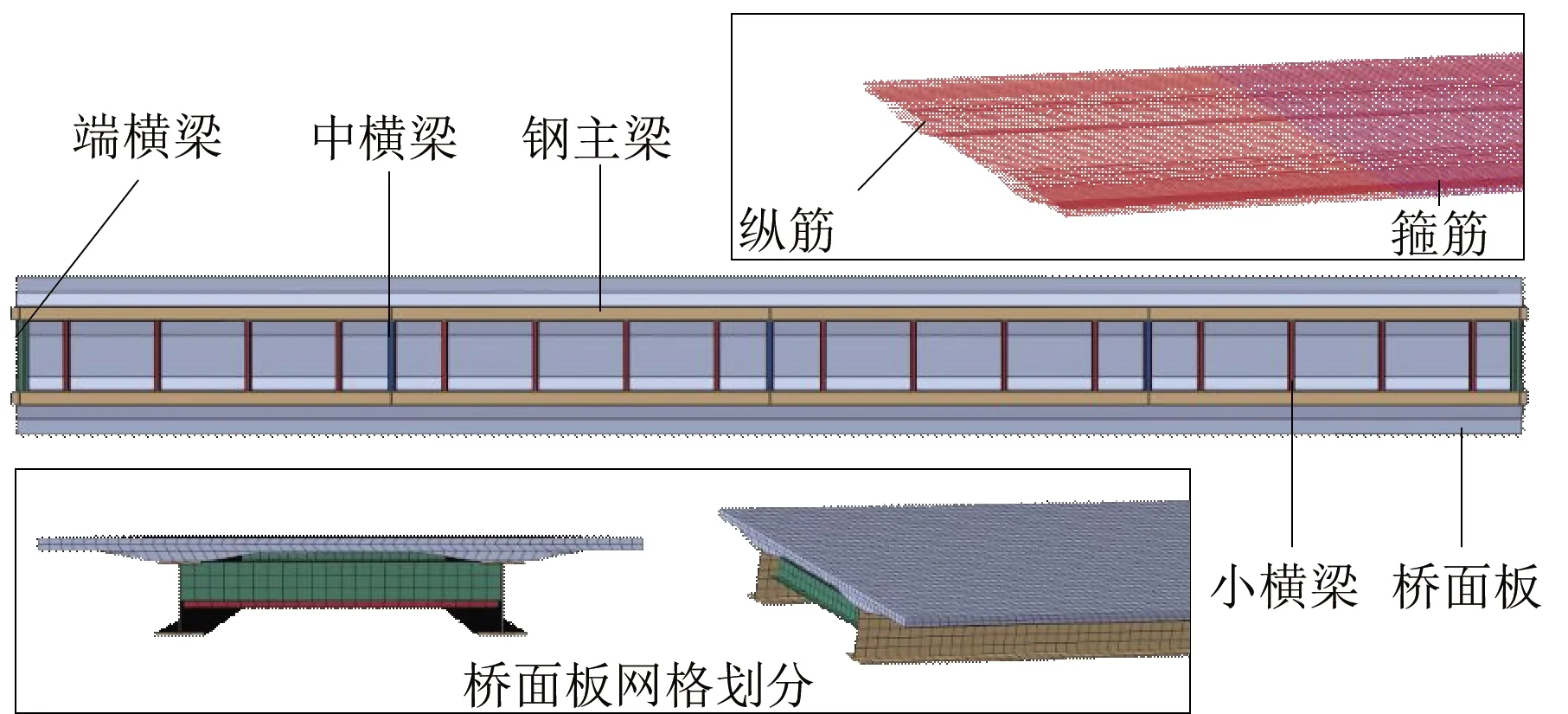
图3 钢-混组合直梁桥分析模型Fig.3 Analytical model of steel-concrete composite straight bridge

图4 规范与有限元结果对比Fig.4 Comparison of analytical results by codes and finite element method(FEM)
参考EC4,若按照图4(b)中的方式来计算等效跨径,即边跨等效跨径取相应跨度的70%,中跨等效跨径取相应跨度的65%;边跨与中跨间的支承处为两跨之和的23%,两个中跨间的支承处为两跨之和的20%,那么计算得到的沿跨径方向的有效宽度结果处于中国规范JTG和日本规范JRA之间,对所有关键截面都能实现包络,且最多只比有限元结果小9.38%,相比日本规范更为经济。
3 连续组合弯梁桥有效宽度分析
3.1 组合弯桥剪力滞效应分析
前文结合各国规范,针对钢-混组合连续直梁桥开展了对比分析。实际上,上述规范大多仅适用于受弯为主的组合梁。对于连续组合弯梁桥,其扭转约束产生的正应力显著,而且由于组合梁桥腹板间距大,桥面板较宽,剪力滞效应更加突出,这种弯扭耦合效应使得混凝土桥面板受力更为复杂。以第1节中的背景桥例为基准,采用ABAQUS软件建立计算跨径为4 m×25 m,曲率半径分别为100、150、200、250 m的连续组合弯梁桥分析模型,其中,基准桥例模型如图5所示。本节主要分析桥梁的自重荷载工况,其余荷载工况的影响规律在后文进一步讨论。
不同曲率半径下混凝土桥面板最边缘处沿顺桥向的正应力分布如图6所示。由图6可见,边跨跨中的应力均大于中跨,边支点处的应力大于中支点,且该四跨连续梁桥沿纵桥向存在多个正应力为零的点。图6(b)中所标识的a、b两个典型截面的正应力分布情况如图7所示。
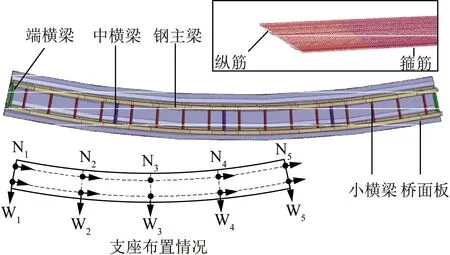
N1~Ns为梁桥内侧1~5号支座;W1~Ws为梁桥外侧1~5号支座图5 钢-混组合弯梁桥分析模型Fig.5 Analytical model of steel-concrete composite curved bridge

图6 不同曲率半径下桥面板顺桥向正应力分布Fig.6 Normal stress distributions along the longitudinal direction of deck with different curvature radii

图7 不同曲率半径下典型断面正应力分布Fig.7 Normal stress distributions of typical cross sections in different curvature radii
由图7(a)可见,由于连续梁反弯点及其附近的混凝土板横断面上同时存在拉、压应力,且应力数值较小,因此,根据有限元结果按照式(1)和式(2)计算得出的有效宽度在反弯点附近可能出现不合理的情况。由图7(b)可见,组合弯桥与直桥在混凝土桥面板的正应力分布方面存在明显区别,其横断面正应力除了受到剪力滞效应的影响,扭转效应产生的影响同样明显,表现为弯桥内侧主梁翼缘板正应力低于外侧主梁,且随着曲率半径的减小,扭转效应对正应力分布的影响逐渐增大,如当曲率半径为250 m时,内侧与外侧主梁的最大正应力相差7.20%;当曲率半径为100 m时,内侧与外侧主梁的最大正应力相差达2.76%。
3.2 组合弯桥有效宽度分析
不同曲率半径下连续组合梁桥面板有效宽度沿着跨长的取值情况如图8所示,因为弯扭耦合效应的影响,特将内、外侧梁分开,同样由于结构对称,图8中仅给出了两跨的结果。由图8可见,内侧主梁的有效宽度受曲率半径的影响更为明显。总体上看,随着曲率半径逐渐变小,支座处的有效宽度变化不大,跨中有效宽度逐渐变小。这一特点在内侧主梁第一跨跨中位置尤为明显,因此选取A1梁段增设3个观测截面进行内、外侧主梁有效宽度的对比如图9所示。
由图9可知,由于内、外侧主梁支座布置不完全一致,直桥内、外侧主梁的有效宽度也存在细微的差异,但是相比弯桥内、外侧主梁的差异,可以忽略不计。随着曲率半径的减小,组合弯梁桥内侧主梁的桥面板有效宽度出现明显的减小趋势。从边跨跨中断面A2来看,当曲率半径为250 m时,内侧主梁对应桥面板的有效宽度比外侧主梁小4.06%;当曲率半径为100 m时,内侧主梁对应桥面板有效宽度比外侧小了9.69%。
由于不同荷载组合对弯桥内力的影响远高于直桥,特别是当车道布载在外侧主梁时。因此,本节设计了三种包含自重、二期恒载、车辆荷载的工况:①工况一,自重、二期恒载和车道内偏;②工况二,自重、二期恒载和车道对称;③工况三,自重、二期恒载和车道外偏。
不同工况作用下,内、外侧主梁的混凝土桥面板最边缘处沿顺桥向正应力的变化趋势如图10所示。
由图10可见,对于内、外两侧主梁,边跨跨中应力均高于中跨跨中应力。对于内侧主梁,内偏车道工况下,跨中和支座处的应力均为最大,外偏车道工况的跨中、支座处应力均为最小;外侧主梁的情况恰好相反。对比图6可以发现,在加上二期恒载和车辆荷载作用后,支座附近的正应力明显增大,且支座N3、W3附近的拉应力小于其余4个中支座附近的拉应力。其中,工况三下的外侧主梁对应的桥面板最为明显,最多比后者低0.68 MPa(38.34%)。
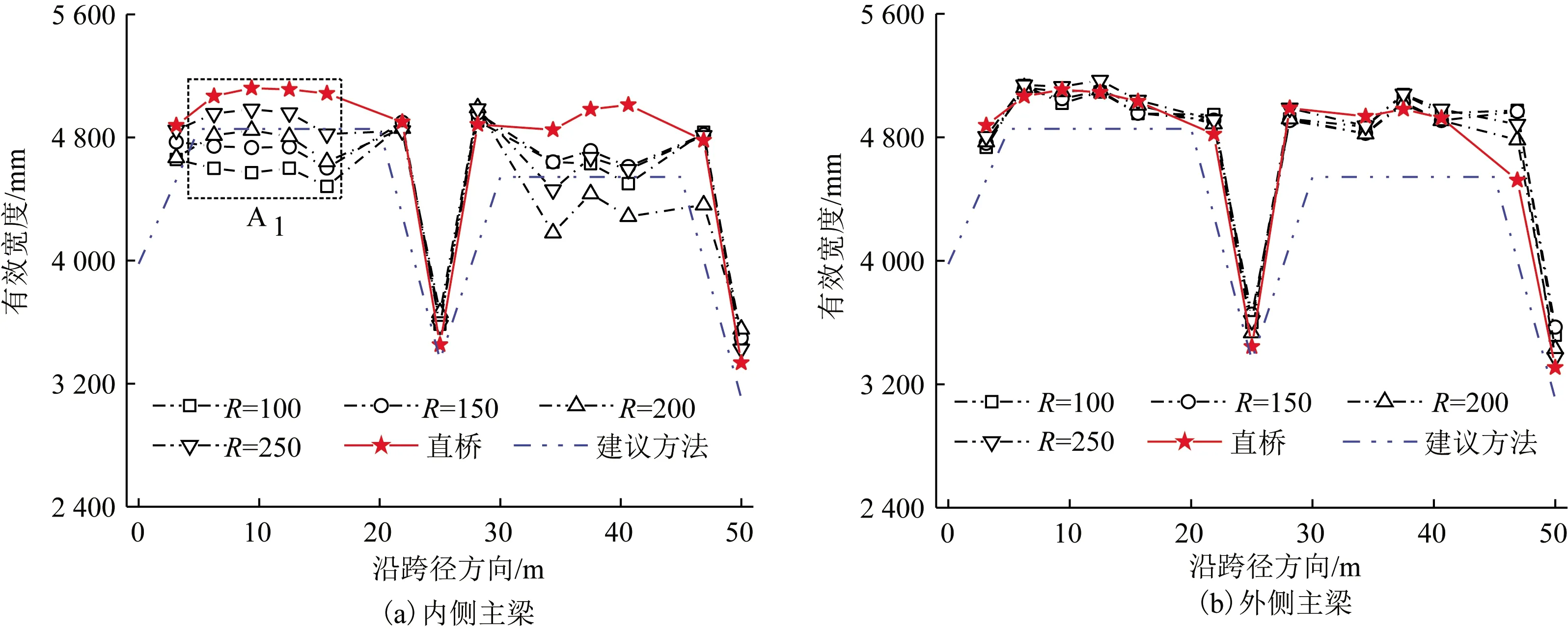
图8 沿跨径方向有效宽度比较Fig.8 Comparison of effective flange widths along spans
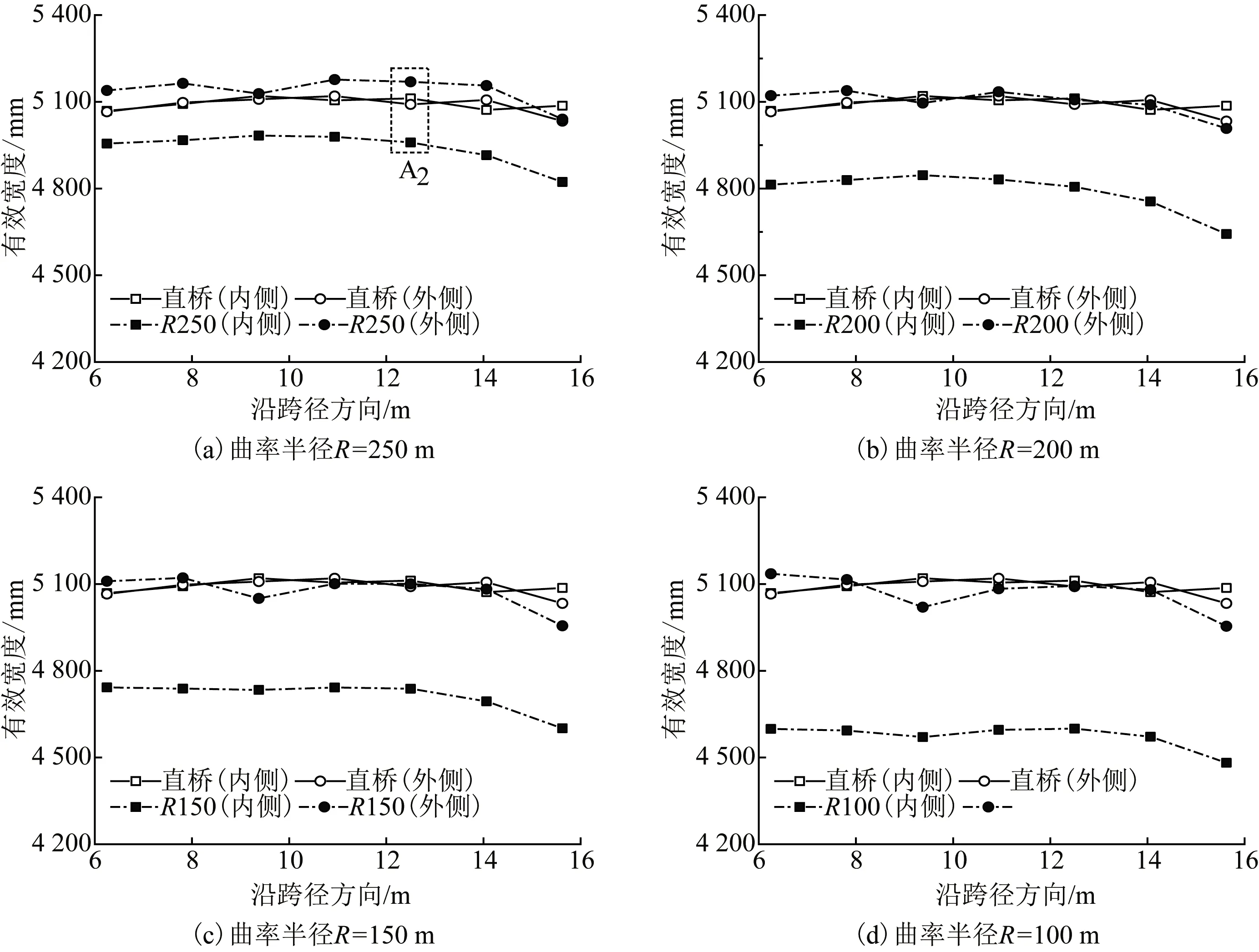
图9 A1梁段内、外侧主梁有效宽度比较Fig.9 Comparison of effective flange widths in A1 portions between inner and outer girders
不同荷载工况下,典型截面的剪力滞系数分布如图11所示,剪力滞系数反应了截面正应力的不均匀分布情况。由图11(a)可见,车道的横向布置位置,直接影响最大正应力出现的位置。在工况一(车道内偏)作用下,内侧桥面板最大压应力比外侧高0.82%,正应力沿横向分布较为对称;在工况二(车道对称)作用下,外侧桥面板的压应力最大值比内侧高18.45%;在工况三(车道外偏)作用下,外侧桥面板压应力最大值比内侧高37.50%。可见,车道布置在外侧的工况加剧了组合弯桥的弯扭耦合效应。从图11(b)中也可以发现类似的现象,即车道的横向布置位置直接影响最大正应力出现的位置,但相比之下,中支座断面的正应力沿横向分布比跨中断面更为对称,说明弯扭耦合效应对支座附近应力分布的影响较小,与图8中支座处有效宽度对曲率半径敏感性不高的现象相对应。
几个关键截面的有效宽度计算结果如表2所示。
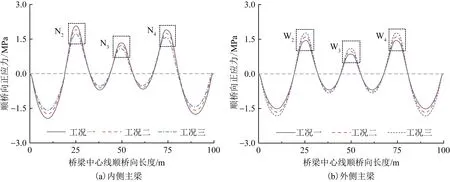
图10 不同荷载工况下桥面板顺桥向正应力Fig.10 Normal stress distributions along the longitudinal direction of deck under different load cases
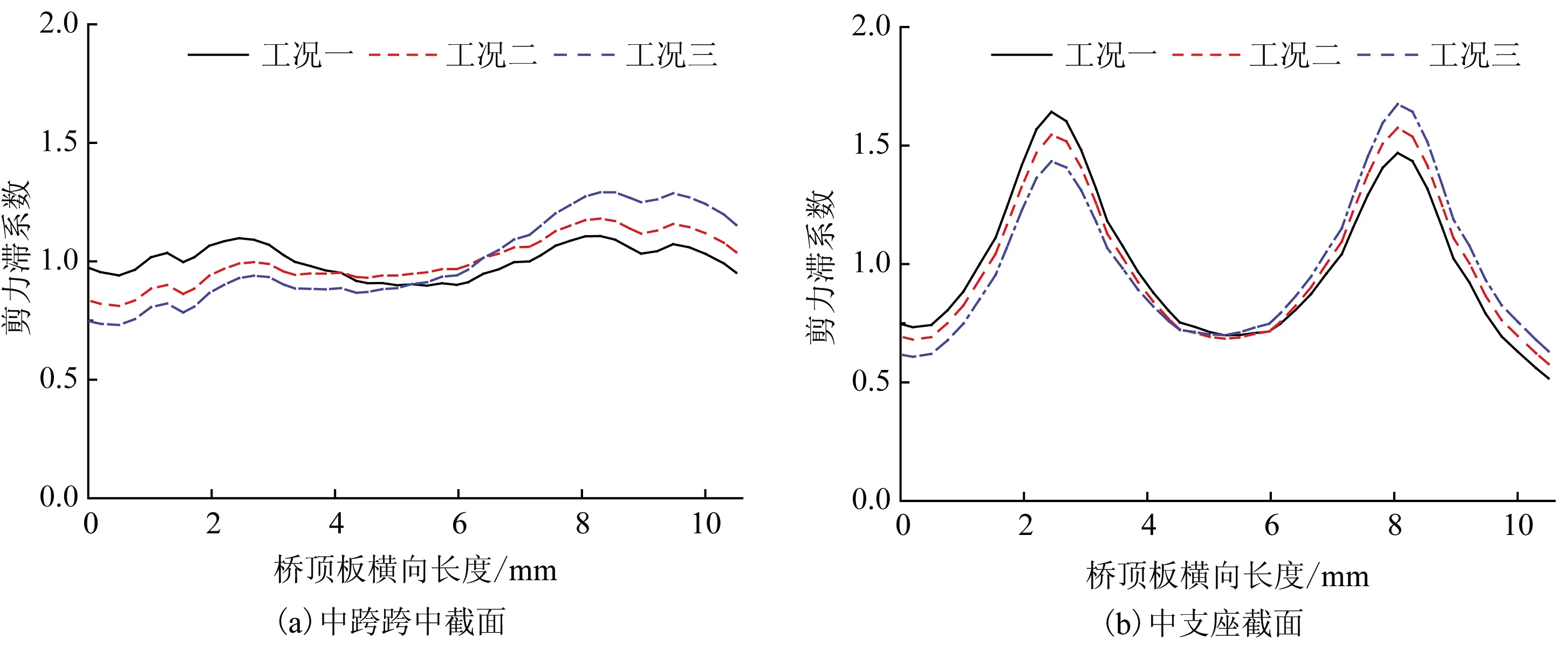
图11 不同荷载工况下典型截面剪力滞系数分布Fig.11 Shear lag coefficient distributions of typical cross sections under different load cases

表2 关键截面有效宽度计算结果Table 2 Calculation results of effective widths of key sections
由表2可知,在跨中断面处,外侧主梁桥面板在工况三作用下的有效宽度明显小于其余三种工况,且当车道偏载时,内、外侧主梁桥面板的有效宽度差值明显大于将车道对称布置的计算结果;在中支点断面处,桥面板受拉应力峰值较大,说明二期荷载、车道荷载使得正应力的不均匀分布加剧,导致该处桥面板有效宽度相比仅考虑自重作用时明显减小。
4 连续组合弯梁桥有效宽度简化计算方法
根据计算结果,选取A1梁段6个控制截面,分别计算每个控制截面对应的直、弯桥的桥面板有效宽度,定义有效宽度比λ1为
(6)
式(6)中:beff,z为直桥的桥面板有效宽度;beff,q为弯桥的桥面板有效宽度。
λ1随曲率半径的变化趋势如图12所示。针对曲率半径在250 m及以下的双工字钢-混组合连续弯梁桥,采用对数函数拟合出λ1的简化计算公式为
λ1=0.42lnR+0.7
(7)
式(7)中:R为双工字钢-混组合连续弯梁桥的曲率半径。
在2.2节所提出的直桥有效宽度建议方法基础上,在正弯矩区乘以相应曲率半径所对应的系数λ1,负弯矩区不变,即可得到相应的双工字钢-混组合连续弯梁桥桥面板有效宽度的简化计算方法,由于建议方法中的系数λ1偏保守,得出的内、外侧主梁有效宽度计算结果相差较小,为了实际设计计算的简便,可统一采用内侧主梁的取法,其具体计算结果如图13所示。由图13可知,在所研究的4种不同曲率半径下,根据简化计算方法得出的有效宽度取值均能包络相应的有限元结果,且计算结果偏安全。
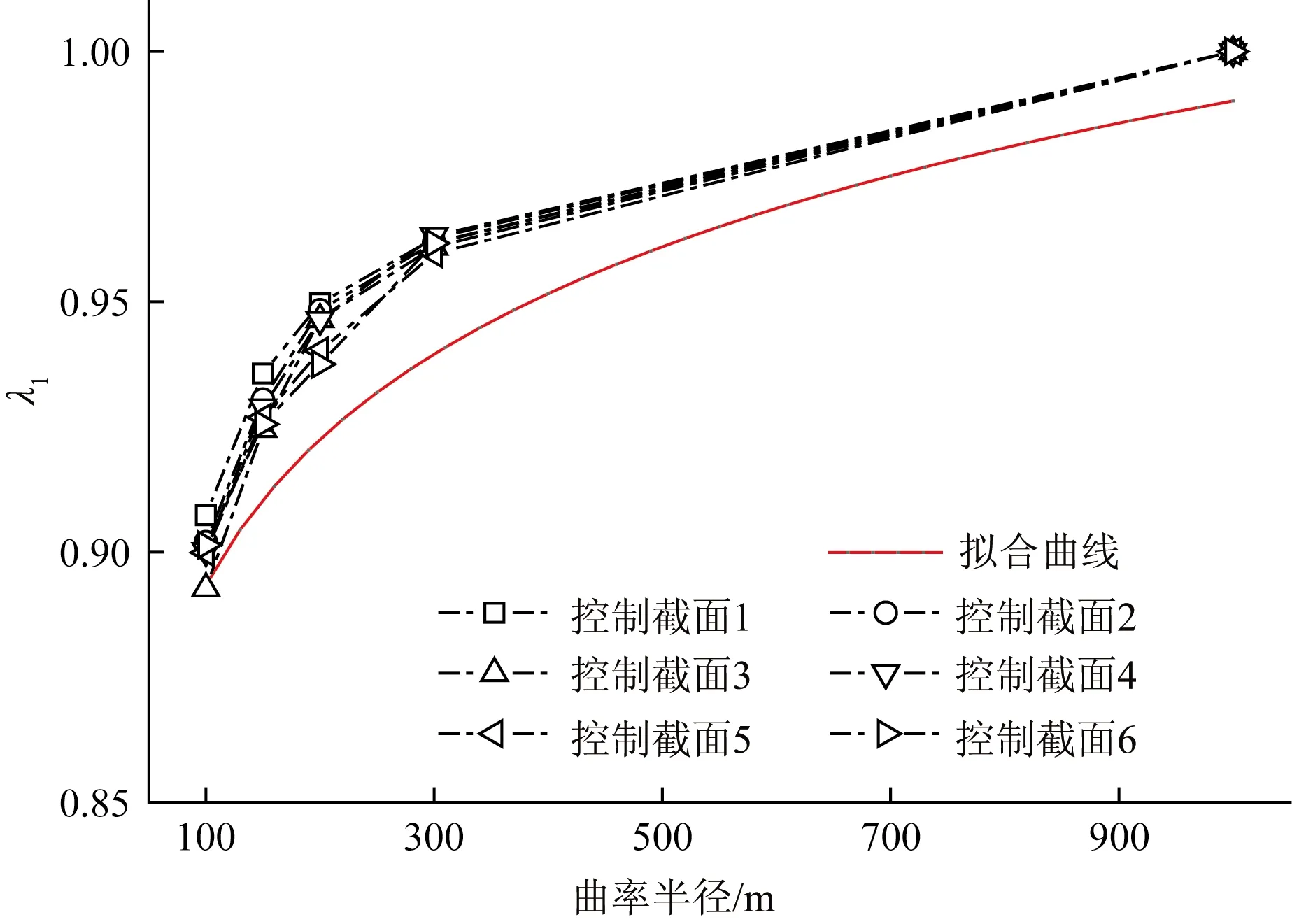
图12 各控制截面λ1值拟合情况Fig.12 Fit conditions of λ1 of each control sections

图13 简化计算方法有效宽度比较Fig.13 Comparison of effective flange widths derived by simplified method
5 结论
(1)双工字钢-混组合连续弯梁桥的桥面板横断面正应力受扭转的影响较大,使内、外侧主梁对应的桥面板正应力分布失去对称性,宜分别计算内、外侧主梁对应的桥面板有效宽度。
(2)随着曲率半径的减小,内、外侧主梁对应的桥面板横断面正应力的不对称性也不断增大,内侧主梁对应的桥面板横断面正应力明显低于外侧主梁,内侧主梁对应的桥面板有效宽度不断减小,而外侧主梁对应的桥面板有效宽度基本保持不变。
(3)荷载大小对双工字钢-混组合连续弯梁桥在支座处的有效宽度取值影响很大,而活载布置方式对跨中区段的有效宽度取值影响很大。车道外偏布置会加剧弯扭耦合效应,从而导致内、外侧主梁对应的桥面板有效宽度的差距增大。
(4)在EC4基础上,提出了钢-混组合连续直梁桥等效跨径的建议划分方式,在此基础上进一步提出小半径连续弯梁桥桥面板有效宽度的拟合修正系数,以此得到的内、外侧主梁桥面板有效宽度简化计算结果能较好地包络有限元分析结果,且计算结果偏保守。
(5)主要结合具体工程,针对现行规范的不足而展开研究,主要用于为小半径双工字钢-混组合连续弯梁桥的桥面板有效宽度计算提供参考,研究结论的普适性有待于进一步的参数分析和试验验证。
