双轴应变对二维IV-VI硫族化合物电子特性的影响*

郭 颖，赵高扬

(1. 西安理工大学 材料科学与工程学院， 西安 710048；2. 陕西理工大学 物理与电信工程学院，陕西 汉中 723001)

0 引 言

2004年，石墨烯首次被剥离出来[1]，开启了一扇基于二维材料理论与实验研究的大门，短短几年间成为举世瞩目的研究热点。原子层厚度的二维半导体材料，由于独特光电性质而在光电子学方面有着潜在的应用前景。二维材料的逻辑器件具有三大优势[2]：(1)二维材料超薄的厚度，使其作为器件的沟道时短沟道效应弱或者不产生短沟道效应，从而使器件门的静电控制能力更强；(2)二维材料侧向没有悬挂键、表面平整，使器件的输运性能更好；(3)二维材料弯曲性好，使其可用于制作柔性可穿戴器件。因此，二维半导体材料被认为很有希望成为未来传统半导体沟道材料的替代品。

摩尔定律表明每隔18个月集成电路上可容纳的晶体管数目会增加一倍，同时性能也提高一倍。在过去的50多年里，晶体管器件的特征尺寸不断缩小，集成度不断提高，因此单个器件的尺寸不断缩短[3]。由于短沟道效应的影响使传统的硅基晶体管几乎不可能满足这一要求，而二维半导体材料可以扩展摩尔定律到亚5 nm。例如，二维MoS2场效应管(FETs)(栅电极：单壁碳纳米管)的物理门长已经可以降低到1 nm的尺度范围[4]。但是MoS2FETs器件的载流子迁移率太低(约150 cm2/(V·s))导致开态电流很小(<250 μA/μm)[5]。虽然二维黑磷烯晶体管的载流子迁移率很高可以达到103cm2/(V·s)，但是黑磷烯本身在室温下非常的不稳定，因此，迫切需要探索其他室温稳定而且性能优异的二维半导体材料。

二维Ⅳ-Ⅵ硫族半导体MXs (M=Sn、Ge；X=S、Se、Te)也被称为类黑磷烯材料，与黑磷烯结构类似且具有各向异性的光电性能。二维 MXs具有适合制作逻辑器件的带隙(0.86 ～1.78 eV)、高达103～105cm2/(V·s)的载流子迁移率。因此，在电子器件(尤其是光电器件)方面有着优异的应用前景。例如：GeSe在光伏器件应用中表现出很好的光学性能，光学吸收系数很高(>104/cm)[6]，在厚度约为一微米时能吸收大部分太阳能[7]；SnSe(SnSe FETs电流开关比可以达到107)[8]、SnS的性能也不俗。实验表明，采用二维MXs为载体制备出来的光电子器件逐渐显露出优越性[9-12]。于是我们对二维MXs的电子性能与哪些因素有关比较感兴趣。

应变工程可以通过提高器件的载流子迁移率[13]和离子注入速度有效地提高硅基场效应晶体管性能。研究表明，施加应变后硅晶体管的开态电流提高了4.5倍[14- 15]。本文研究应变工程对二维 MXs的电子性能的影响并阐明其内在规律，进而为将来制作高性能的逻辑器件提供理论依据。

1 方法与模型

本文采用基于密度泛函理论(density function theory，DFT)的VASP(vienna Ab initio simulation package)软件程序包进行模拟计算。几何结构优化和电子特性计算选用缀加平面波赝势(projector augmented wave，PAW)描述电子-离子相互作用。电子波函数通过平面波基组展开，电子与电子之间相互作用的交换关联采用广义梯度近似(generalized gradient approximation, GGA)下的Perdew-Burke-Ernzerhof(PBE)交换泛函形式。经过收敛性检验，在该体系下的结果表明平面波截止能量选为400 eV最为合适。在弛豫的过程中：原子位置、晶格参数及单胞体积等几何结构都进行了完全弛豫, 直到原子上的受力收敛于0.001 eV/0.1 nm为止；收敛精度为1×10-6eV/atom；布里渊区的k点网格采用9×9×1 (由Monkhorst-Pack方案自动生成, 以Gamma为中心)。在计算电子能带时，布里渊区采用的k点网格为24×24×1。计算采用半经验的DFT-D3方法考虑范德瓦尔斯相互作用。在z方向采用偶极子修正，以防体系不对称时赝的偶极矩相互作用。

2 结果与讨论

2.1 二维MXs的本征特性

单层 MXs弛豫后的晶体常数为a和b、各向异性参数和带隙如表1所示。其结构俯视图和侧视图如图1(a)和(b)所示。MXs具有类似黑鳞的结构，3个X原子与一个M原子配位形成puckered的M- X层。

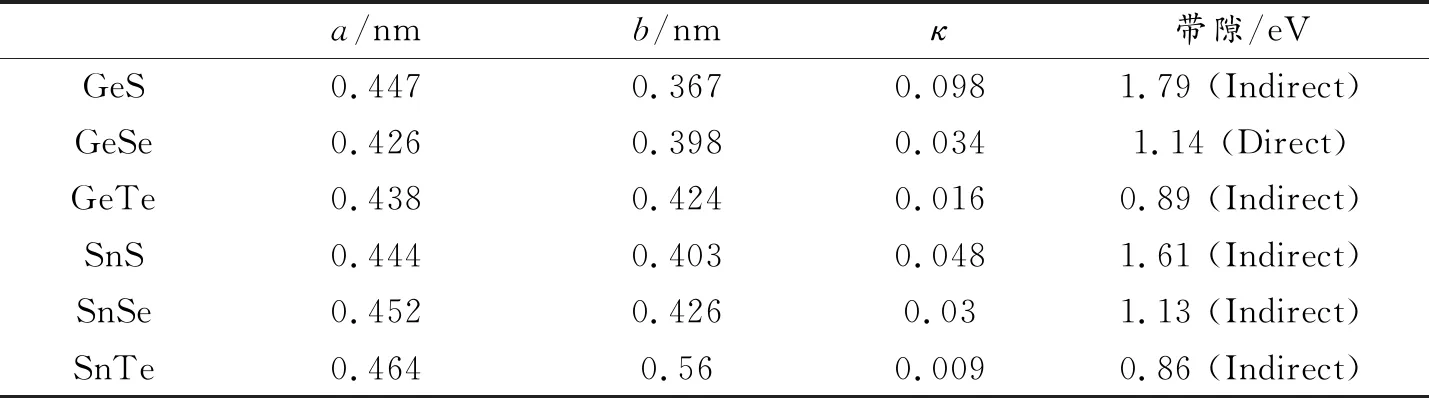
表1 单层MXs的晶格常数、各向异性因子和带隙值

图1 单层MX晶胞俯视图(a)和侧视图(b)虚线矩形表示单胞的大小，晶格常数分别为a和b双向箭头表示在晶胞的ab面施加双轴应变

图2为单层MXs的本征能带图。由图可知，单层MXs中GeSe为直接带隙，其他MXs都为间接带隙；GeSe的直接带隙位于X-Г的区间内，其他MXs的间接带隙都在X-Y的区间内。其值(见表1) 范围为0.86～1.78 eV，带隙的大小依次递增为：SnTe (0.86)0.4 eV特别适合应用于场效应管的沟道材料，而且与太阳光谱匹配的很好适合制备成光电探测器[23]。

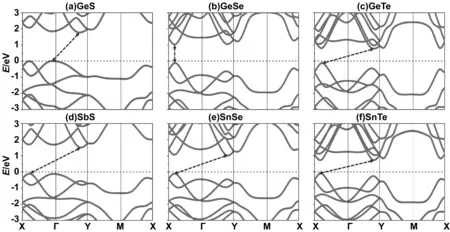
图2 单层MXs的能带结构图

单层MXs的带隙在相同的X元素下，GeX的带隙比SnX的带隙大，这是因为Ge和X原子之间的相互作用更强。研究还发现，当M (Ge或Sn)为一定值时，从Te到Se再到S，单层MXs的带隙和结构各向异性因子κ随着X的减小而增大，这是由于原子轨道减小，M与X的相互作用增强所致。这些结果与其他二维过渡金属二硫族化合物和III族硫属化合物的结果一致[24-26]。

2.2 双轴应变对二维MXs的光电性能影响

已经有文献报道利用施加应变的方法可以有效的调节二维材料和其准一维形式的电子、光学和输运的性质[27-28]。而在实验室制备二维MXs材料或者二维 MXs器件时，基底材料和电极材料会改变MXs的晶格常数，相当于给MXs施加了应变。因此为了形象的、理想的把这种应变表现出来，本文模拟实施双轴应变对二维MXs的电子特性影响。本文的双轴应变ε同时施加在armchair和zigzag方向(如图1所示)。ε<0表明给单层MXs施加了压缩应变，ε> 0表明应变为拉伸应变，|ε|值越大表示应变越大。当应变太大时MXs材料会严重变形甚至不成形，因此我们的应变范围控制在-5% ≤ε≤ 5%之间。施加这种程度的应变既能说明应变对材料性能的影响，又不会破坏材料本身。

图3为双轴应变从-5%曾加到5%时单层GeS的能带结构。施加双轴应变后单层GeS的色散关系变化不大，但是带隙变化比较大，说明带隙对应变比较敏感。间接带隙在应变作用下可调范围为：0.94 ～1.89 eV，且随ε值的增加而增加，在ε为2%时达到极大值1.89 eV，随后随ε的增加而缓慢减少。单层SnS在应变作用下的带隙变化与GeS相似(如图4所示)，带隙变化范围为：1.13～1.72 eV，带隙也随ε值的增加而增加在ε为2%时达到极大值1.78 eV，随后随ε的增加而缓慢减少。单层GeS和SnS的价带顶(valence band maximum，VBM)都一直保持在费米能级附近，但是在ε>0时VBM位于Г点，而ε<0时位于X-Г的区间内。ε≥ 3%时导带底(conduction band minimum，CBM)位于X-Г的区间内，-3%≤ε≤2%时CBM位于Г-Y的区间内，ε为-4%和-5% 时CBM位于X-Г的区间内，但是来自于不同的色散曲线。

图3 单层GeS在双轴应变为ε=±1%、±2% 、±3%、±4%、±5%时的能带结构图

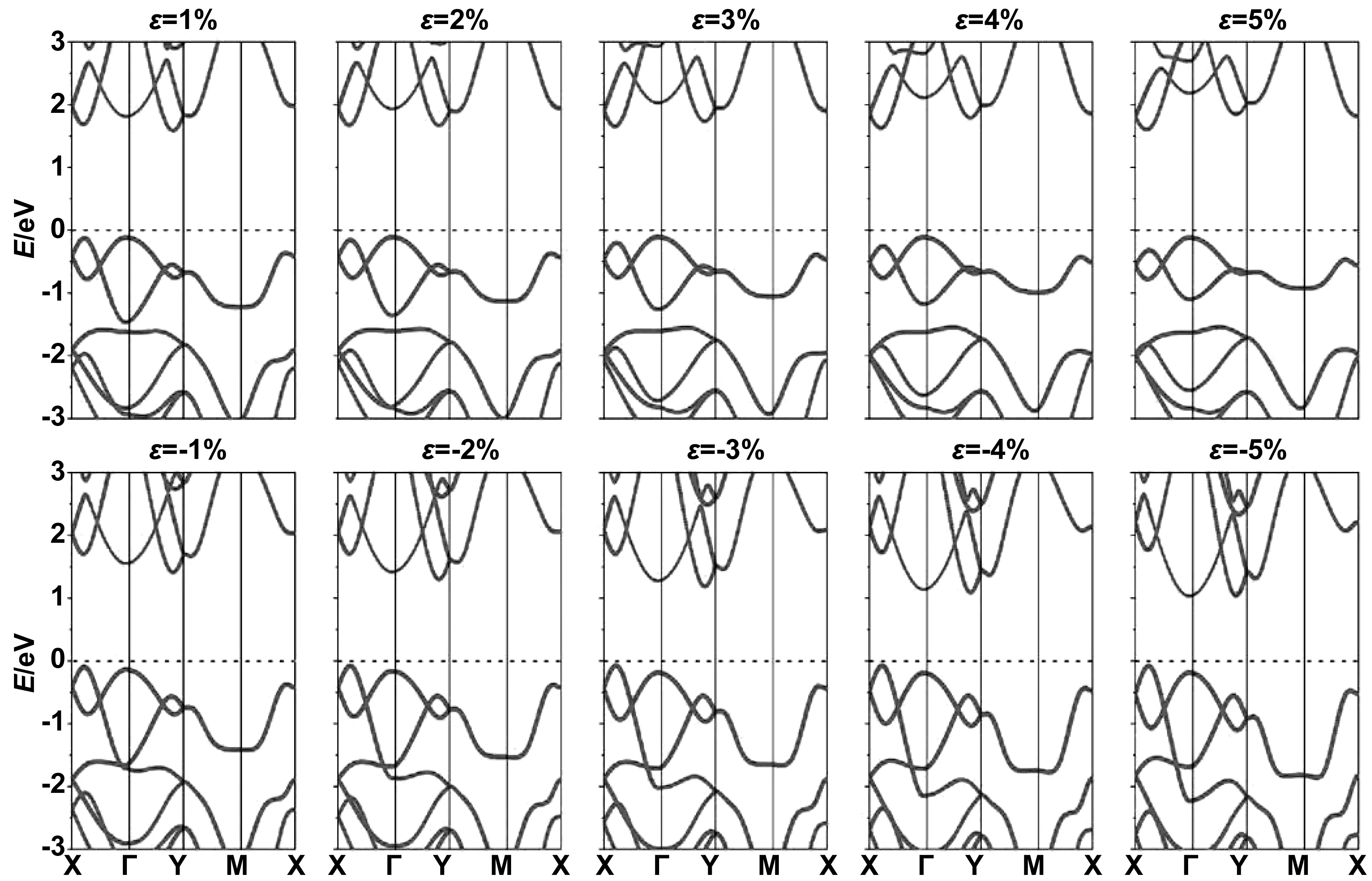
图4 ML SnS在双轴应变为ε=±1%、±2% 、±3%、±4%、±5%时的能带结构图

图5 ～8为GeSe、GeTe、SnSe和SnTe在双轴应变(-5%≤ε≤5%)作用下的能带结构图。施加双轴应变后单层MXs的色散关系变化不大，但是带隙相对变化大，说明带隙对应变敏感。单层MXs的带隙值变化范围分别为：(GeSe)0.23～1.46 eV、(GeTe)0.07～1.16 eV、(SnSe)0.26～1.44 eV和(SnTe)0.27～1.14 eV。

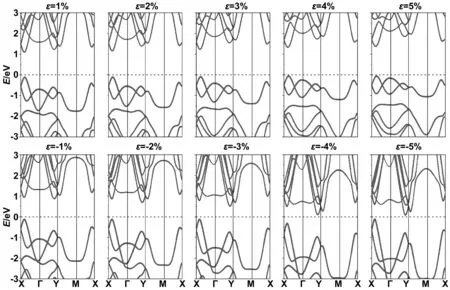
图5 单层GeSe在双轴应变为ε=±1%、±2% 、±3%、±4%、±5%时的能带结构图

在光电器件的实际应用中，由于直接带隙的半导体材料的发光效率高，更适合做光电器件，因此具有直接带隙的半导体材料更受光电器件的青睐。本征MXs带隙中只有GeSe是直接带隙，可喜的是当施加拉伸应变后，即ε> 0时，GeTe、SnSe和SnTe都变成直接带隙，并且处于X-Г区间内。说明双轴拉伸应变可以将间接带隙变成直接带隙。为进一步研究MXs的光电器件提供了一种途径。而且还发现当ε由拉伸应变变为压缩应变后带隙由直接带隙变为间接带隙(包括GeSe也在拉伸应变的作用下变为间接带隙)。VBM一直保持在费米能级附近，位于X-Г区间内。而CBM由X-Г区间(拉伸应变)变化为在Г-Y的区间内(压缩应变)。当压缩应变最大时单层 MXs的带隙都达到了本次模拟的最小值，(GeTe的最小值为0.07 eV，近似为赝的导体)可以预见如果继续增加压缩应变，单层 GeSe、GeTe、SnSe和SnTe的带隙将为零，单层 MXs将由半导体变成导体。有文献已经报道当压缩应变继续增加(ε≤-6%)时，GeSe的带隙为零，半导体特性消失而具有金属性[29]。

图9为最大压缩应变与最大拉伸应变对单层MXs带隙的改变量。当施加压缩应变(ε<0)时，单层MXs带隙的总改变量分别为：0.85(GeS)、 0.91(GeSe)、0.82(GeTe)、0.48(SnS)、0.87(SnSe)和0.59(SnTe) eV，如柱图标注。当施加拉伸应变(ε>0)时，带隙的总改变量分别为：0.096(GeS)、 0.32(GeSe)、0.27(GeTe)、0.17(SnS)、0.31(SnSe)和0.28(SnTe) eV，如柱图标注。对于同种单层 MXs拉伸应变对带隙的改变量小于压缩应变的作用。说明压缩应变对带隙的影响大于拉伸应变。

图7 ML SnSe在双轴应变为ε=±1%、±2% 、±3%、±4%、±5%时的能带结构图

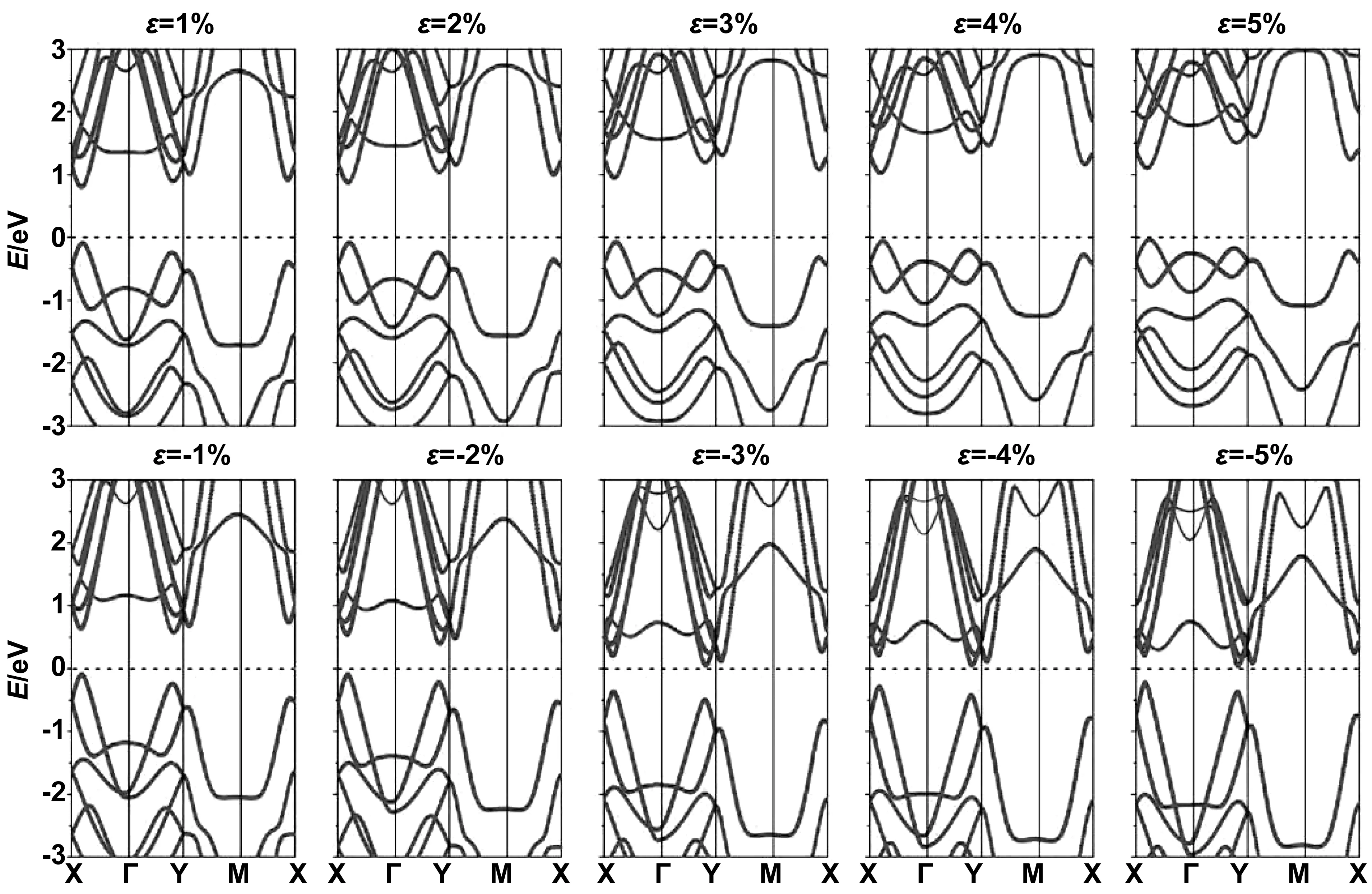
图8 ML SnTe在双轴应变为ε=±1%、±2% 、±3%、±4%、±5%时的能带结构图

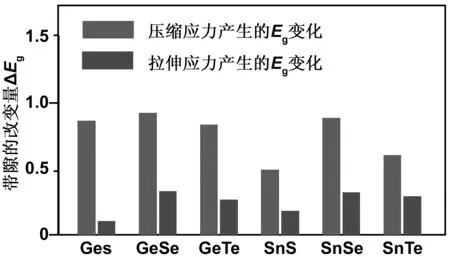
图9 最大压缩应变与最大拉伸应变对单层MXs的带隙改变量

图10(a)和(b)分别为单层MXs的带隙(Eg)和费米能级与所施加的双轴应变(-5%～5%)的关系图。从带隙与应变关系可以看出：GeS和SnS的带隙变化随应变的增加呈近似抛物线状，带隙的可调范围相对较小，分别为：0.94和0.65 eV。其他MXs(GeSe、GeTe、SnSe和SnTe)的带隙变化随应变的增加单调增大，其中GeSe的带隙变化范围最大为1.23 eV，而SnS的带隙变化范围最小为0.65 eV。在图中用实心符号表示直接带隙，空心符号表示间接带隙。ε=0时只有GeSe为直接带隙，但是当施加拉伸应变时GeSe、GeTe、SnSe和SnTe都是直接带隙。不同的是GeSe继续保持本征带隙，而GeTe、SnSe和SnTe由本征的间接带隙变成直接带隙。而当施加压缩应变时，GeTe、SnSe和SnTe又变回本征的间接带隙，而GeSe变成与本征带隙不符的间接带隙。可见在单层MXs中不仅可以用应变调整带隙大小，还可以调节直接带隙与间接带隙之间的变换。

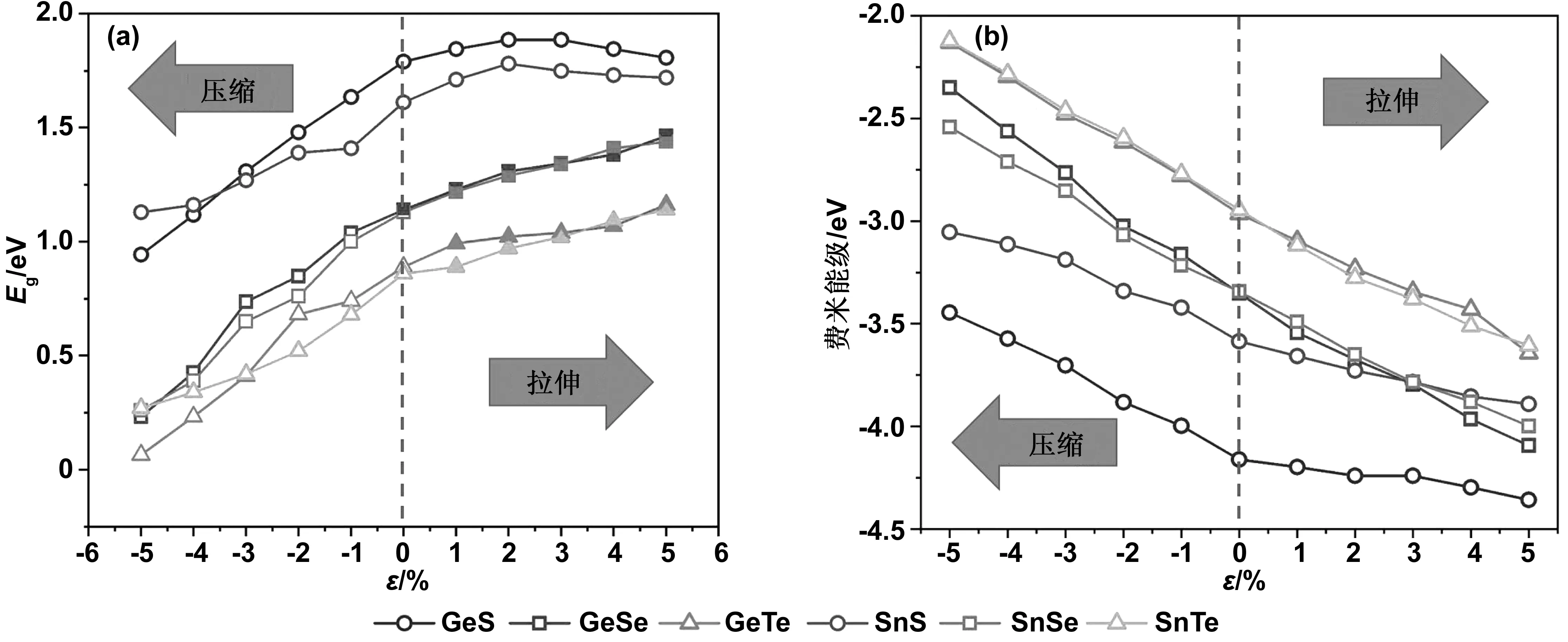
图10 单层MXs的带隙(a)和费米能级(b)与双轴应变(范围-5%～5%)的关系

图10(b)可以看到，在双轴应变的作用下单层MXs的费米能单调下降，ε值越大费米能级越低。其中GeS和SnS的费米能级下降较缓慢，分别降低了了0.91和0.84 eV。GeSe的费米能下降最多为1.74 eV，SnSe、SnTe和GeTe的费米能分别下降1.46、1.48和1.51 eV。费米能级受到双轴应变的影响，同样也是压缩应变的影响大于拉伸应变的：压缩应变时费米能级的总降低量分别为0.72(GeS)、 1.00(GeSe)、0.83(GeTe)、0.53(SnS)、0.80(SnSe)和0.82(SnTe) eV大于拉伸应变时费米能级的总降低量(0.20(GeS)、 0.74(GeSe)、0.68(GeTe)、0.31(SnS)、0.66(SnSe)和0.66(SnTe) eV) 。

3 结 论

采用DFT模拟研究了单层 MXs在双轴应变(-5%～5%)作用下能带结构、带隙和费米能级等的电子性质变化情况。研究发现当M (Ge或Sn)确定时，由于从Te→Se→S的原子轨道减小，因此M与X的相互作用增强，致使单层MXs的带隙和结构各向异性因子κ随着X的减小而增大。应变不仅可以调整单层MXs的带隙大小，还可以调节GeSe、GeTe、SnSe和SnTe的直接带隙与间接带隙之间的转换。GeTe在最大压缩应变下带隙趋于零，如果持续增加压缩应变，可以使其变成导体。发现压缩应变对带隙的影响大于拉伸应变。单层MXs的费米能级受双轴应变的影响单调下降，随ε值的增加而降低，且压缩应变的影响大于拉伸应变的影响。研究结果有助于充分发掘单层MXs在光电器件领域的应用潜力，对如何调控二维半导体材料的禁带宽度提供了一种有效的方法，进而为设计出高性能的二维半导体器件的沟道材料提供理论依据。