不平衡电网下的改进型锁相环设计研究
2022-02-17张华赢胡子珩李艳艾精文
张华赢,胡子珩,李艳,艾精文
(深圳供电局有限公司电力科学研究院,广东 深圳518020)
0 引 言
对大多数并网变换器,如有源电力滤波器、不间断电源、分布式电源,电网电压频率、幅值和相位等信息的准确获取具有重要意义[1-2]。
在实际应用中,基于闭环的锁相环(Phase Locked Loop,PLL)由于其结构简单和实现灵活,是最广泛使用的电网同步算法。在三相系统中最常使用的是基于同步坐标系的锁相环(synchronous reference frame PLL,SRF-PLL)[3-5]。在SRF-PLL中,首先将三相电网电压(va、vb和vc)转换到同步坐标系中,得到d、q轴电压分量vd和vq,然后通过反馈机制将vq调节为零来获取电网电压相位。当电网电压为理想正弦波时,SRF-PLL具有很高的带宽,可快速和准确的估计相位。但是,如果输入信号三相不平衡,则需要减小SRF-PLL的带宽以进行适当的滤波。为了消除负序分量的影响,会造成SRF-PLL带宽过低,从而系统动态响应无法满足应用需求。为提高锁相精度,可在传统PLL之前串联低通滤波器[6],但此方案存在系统响应变慢、附加相位偏移等问题。文献[7]基于二阶广义积分器(Second-order Generalized Integral,SOGI)提出了一种可频率自适应的三相锁相方法。在电网不平衡时仍能准确锁定基波相位,但对3、5、7等低次谐波的滤除效果不是很明显,所以稳态时,相位检测精度不高。文献[8]采用解耦双同步坐标系锁相环(Decoupled DSRF-PLL,DDSRF-PLL)来实现不平衡电网条件下的准确锁相。DDSRF-PLL中包含两个角速度相同,但旋转方向相反的同步坐标变换,结合一个解耦网络来提取电网电压的正序基波分量。但是,DDSRF-PLL依赖于锁相相位反馈,因此,电网相位突变时会导致动态过程中存在超调、稳定时间长等问题。基于自适应观测器(FRF)[9]的方法可以较准确的进行锁相,但是该算法实现复杂,占用DSP资源较多。
文章从提取电压正序基波出发,分析了SOGI能实现信号正交化和滤波的原理。通过频域分析,针对传统SOGI消除直流偏移和抗谐波干扰能力弱的特性,提出增强其滤除零频和低次谐波能力的改进方案,并从理论上对其进行性能校验。最后,利用PSCAD软件搭建出包含该锁相环在内的几种锁相环仿真模型,在多种电网环境条件下进行仿真对比试验,仿真结果证明了所提方案的有效性。
1 电压正、负序分离原理
在电网三相不平衡时,对于SRF-SPLL而言,由于电压负序分量的存在,从而导致其锁相不准确。因此,电网不平衡时,为保证锁相准确需要提取出正序基波信号。不平衡电网电压中含有正、负、零序分量,此时可以表示为:
(1)
(2)
(3)
在本文研究中,零序分量不予考虑。经过数学变换可得[10]:
(4)
(5)

2 SOGI的频率特性
SOGI的结构如图1所示[11]。
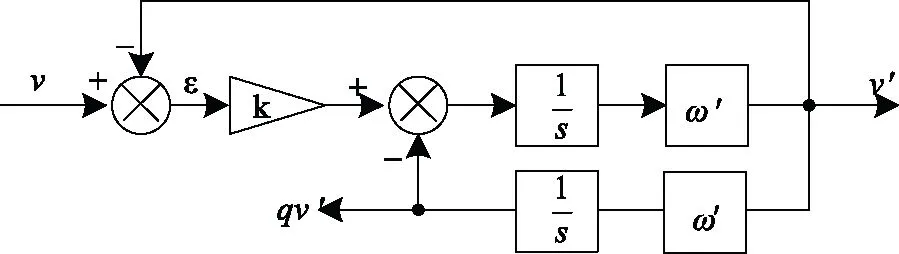
图1 SOGI结构图Fig.1 Diagram of SOGI
由图1可得如下传递函数:
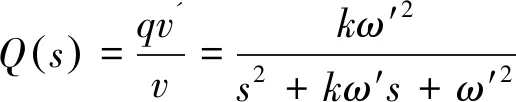
式中ω′为谐振频率;k是阻尼系数;v为输入信号。图2是系统在不同k值时的伯德图。
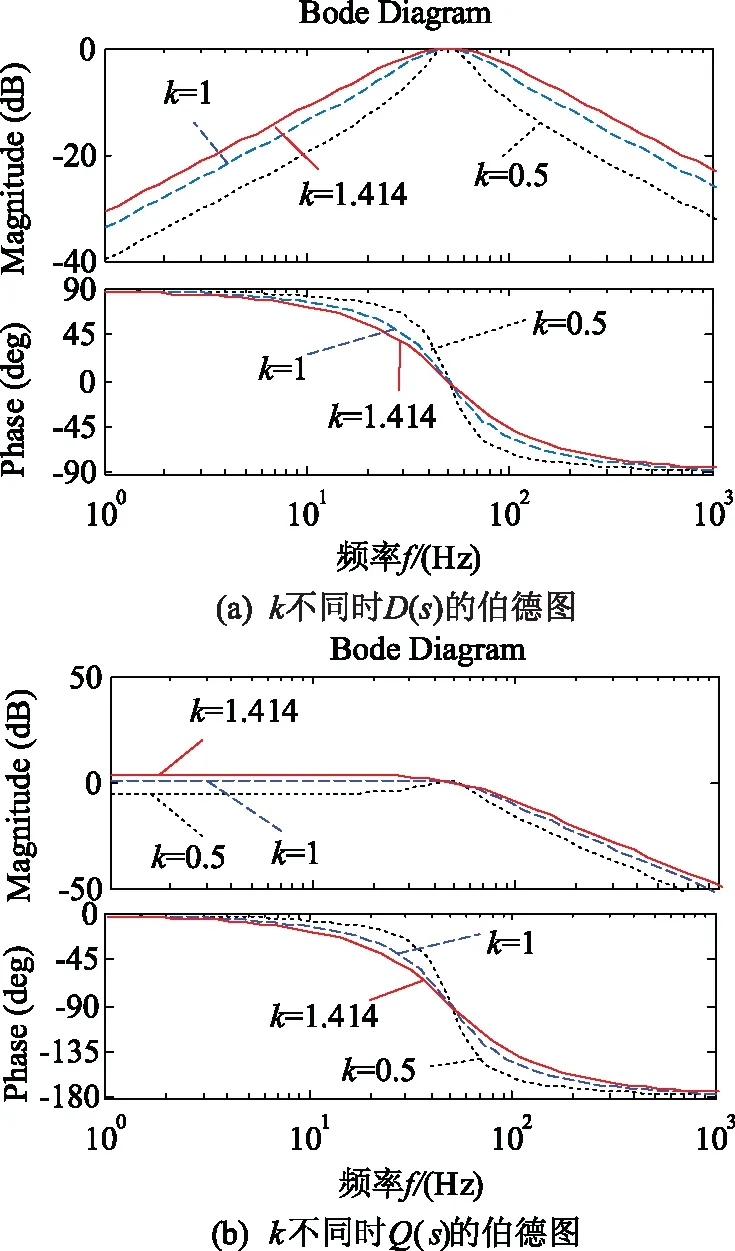
图2 SOGI的频率特性Fig.2 Frequency characteristic of SOGI
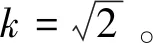
分析式和式,当ω′与v的频率相同时,则v′与v具有相同的相位和幅值;qv′与v具有相同的幅值,但相位滞后90°。基于此,结合式,可设计出如图3所示基于双二阶广义积分器(DSOGI)的传统型锁相环。
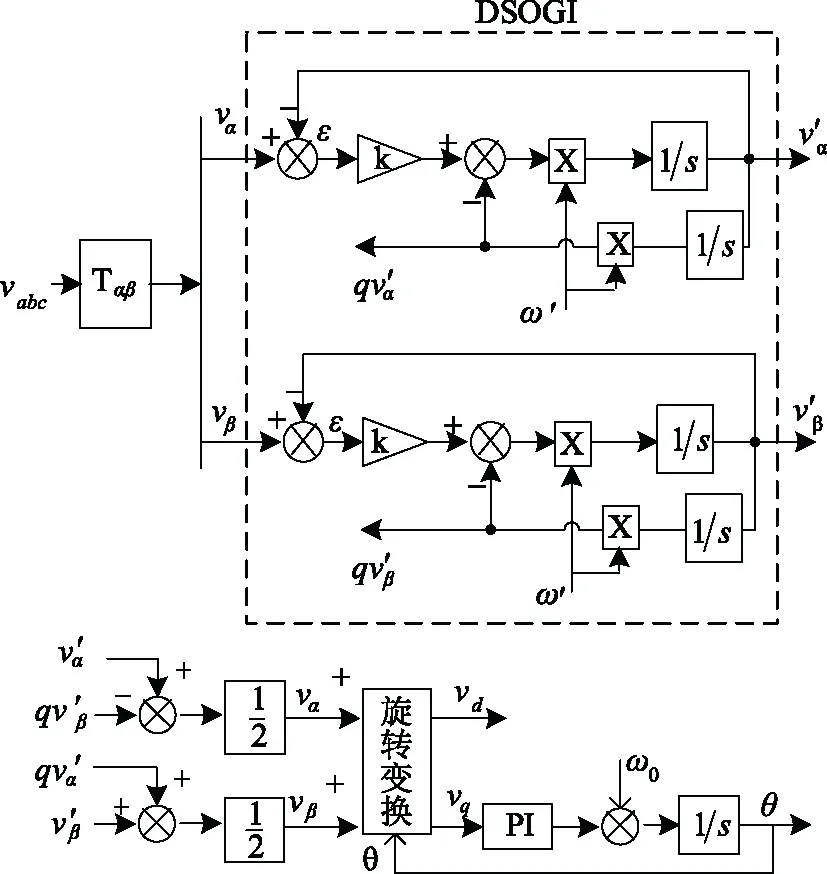
图3 DSOGI-PLL结构框图Fig.3 Block diagram of the proposed DSOGI-PLL
3 改进型SOGI及其拓展应用
分析图2(b)可知,Q(s)是一个低通滤波器,一旦输入信号包含直流分量那么输出信号qv′很容易受到影响,导致电压正序分量提取存在误差,从而降低锁相精度。在实际应用中,由于各种原因导致检测到的电网电压会含有直流分量。因此,提出一种能消除直流分量影响的SOGI结构,如图4所示。
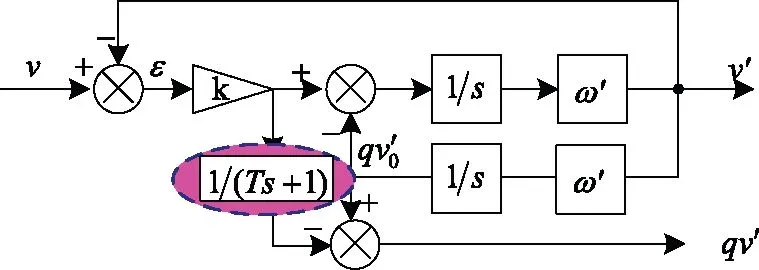
图4 改进的SOGI结构框图Fig.4 Block diagram of the improved SOGI
从结构图中可以分析得知:ε=v-v′,当系统稳定时,ε中包含v中的所有直流分量。
因此可以在ε经过增益k放大后,再通过低通滤波器,与qv′做差,这样可彻底消除掉信号qv′中的直流量。为兼顾系统动态性能与高频衰减能力,选取图4中低通滤波器的截止频率ωc为80π(T=1/ωc),图5为改进后Q(s)的伯德图。
由图5可以看出,改进后的Q(s)在零频处的增益大大降低,因此能很好地消除掉直流分量的影响。
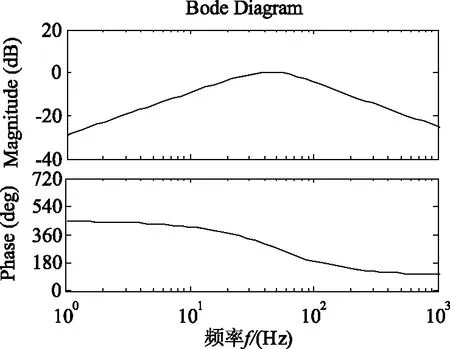
图5 改进型SOGI中Q(s)的伯德图Fig.5 Bode plot of Q(s) in the improved SOGI
无论传统型SOGI还是改进型SOGI,都存在低次谐波滤除能力不够的问题。当低次谐波不能忽略时,会导致检测到的频率及相位信息存在小幅低频波动。虽能通过减小滤波器带宽来削弱其影响,但这样会减小锁相环系统带宽,从而降低系统的响应速度。针对这个问题,采用如图6所示多滤波器并联的结构来消除低次谐波干扰,以提取出电压正序分量。
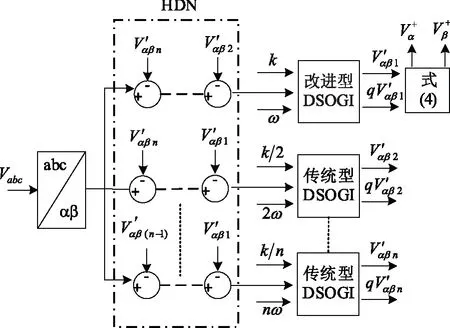
图6 多DSOGI并联结构Fig.6 Block diagram of parallel DSOGI
对于图6的并联结构,可以将kn设为k/n(k为基波DSOGI的阻尼系数)。这样的话,可以使得各次滤波器的knωn相同,从而各DSOGI具有相同的带宽。
由于HDN模块中只用到 分量,根据前述分析可知经SOGI滤波得到的 并不受直流分量影响。因此,为简化系统结构,在图 6中只有基波DSOGI采用所提改进型SOGI,那么所设计的电压正序分量提取模块既能消除掉直流分量的影响,又能大大增强对于低次谐波分量的抑制能力。
4 仿真验证
基于PSCAD仿真软件搭建出三种类型锁相环,分别是:(1)图3所示基于传统DSOGI的锁相环(A型);(2)将图 3中的SOGI换为本文所提改进型SOGI的锁相环(B型);(3)基于图6所示电压正序分量提取模块的锁相环(C型)。仿真时,C型锁相环中为3次和5次谐波分量设置了对应的DSOGI模块,且各个锁相环仿真模型中的PI控制器参数均一致。仿真结果中以锁相所得d轴定向电压Ud和电网基波频率f两个参数作为指标来衡量锁相环性能的好坏。分别在三种情况下对各类型锁相环进行仿真测试:(1)初始电压信号为基波正序电压,幅值为220 V(最大值),在0.2 s时,叠加上0.2 p.u.的基波负序分量;(2)初始电压信号为基波正序电压,幅值为220 V,在0.2 s时,在A、B两相信号中分别叠加上10 V的直流量;(3)初始电压信号为基波正序电压,幅值为220 V,在0.2 s时,叠加上0.15 p.u.的3次分量以及0.1 p.u.的5次分量;仿真结果如图7~图9所示。
从图7(a)和图7(b)中的初始阶段(即理想电网情况下),可以看出三种类型的锁相环均能准确地锁定电网电压的频率及幅值。当三相电压发生不对称突变时,A型锁相环由于在结构上较其他两种类型的锁相环简单,因此其动态响应最快,过渡过程所用时间最短。三种锁相环都利用SOGI从不平衡电压中提取出正序基波分量来进行锁相,因此在不平衡电网环境下都具有较高的稳态精度。
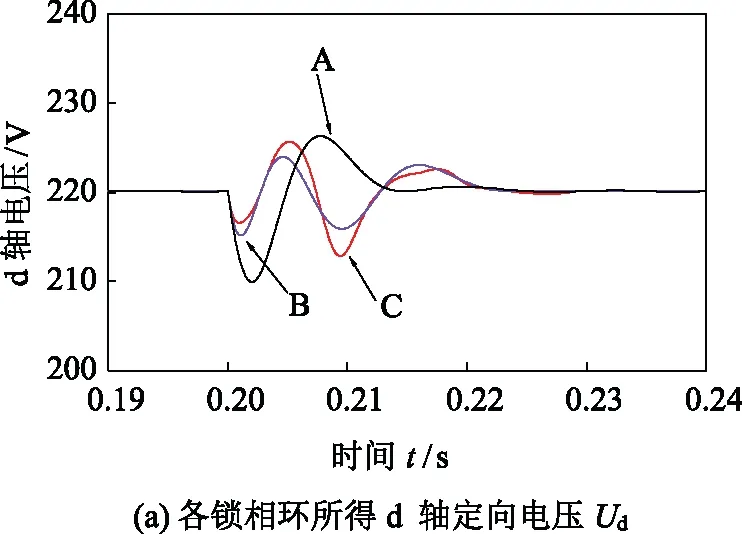
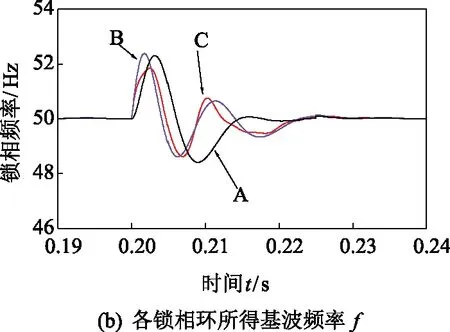
图7 条件1下仿真结果Fig.7 Simulation results in case 1
分析图8(a)和图8(b),当三相电压信号中含有直流分量时,A型锁相环受到直流分量的影响,稳态时的Ud和f均含有近工频周期的波动分量,而B型和C型在稳态时的锁相精度几乎不受影响。因此,改进型SOGI能够有效消除直流分量的影响。
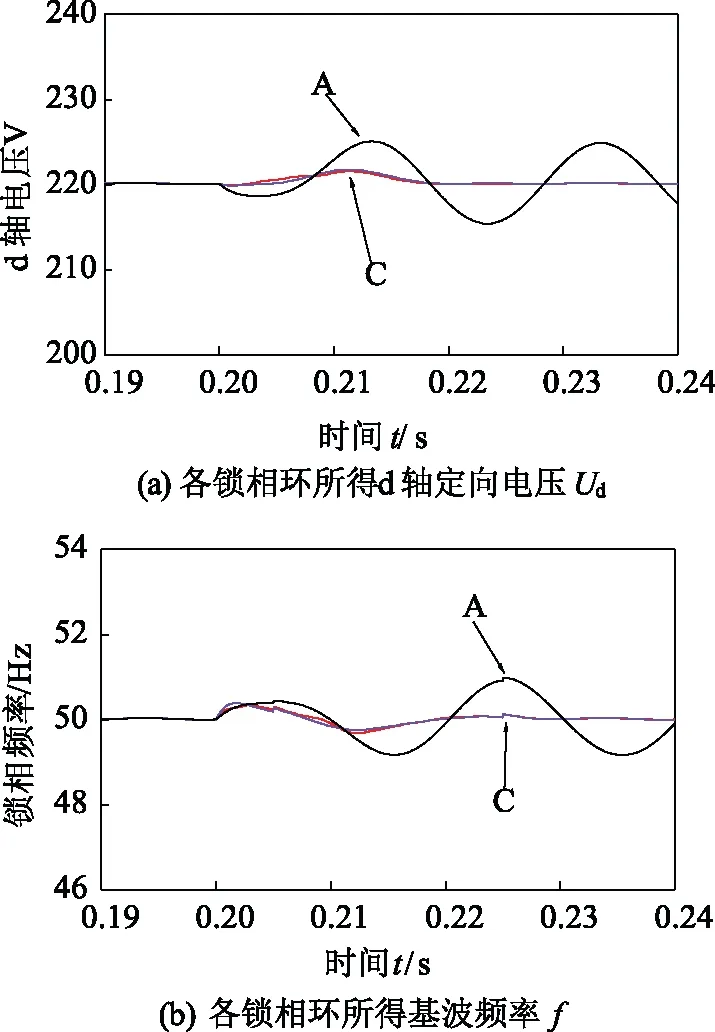
图8 条件2下仿真结果Fig.8 Simulation results in case 2
根据图9(a)和图9(b),A型和B型锁相环因受谐波分量影响,两者的锁相性能均大幅下降;而C型锁相环仍能保持较高锁相准度。因此,图6所示的多DSOGI并联结构,具有较强抗谐波干扰能力。
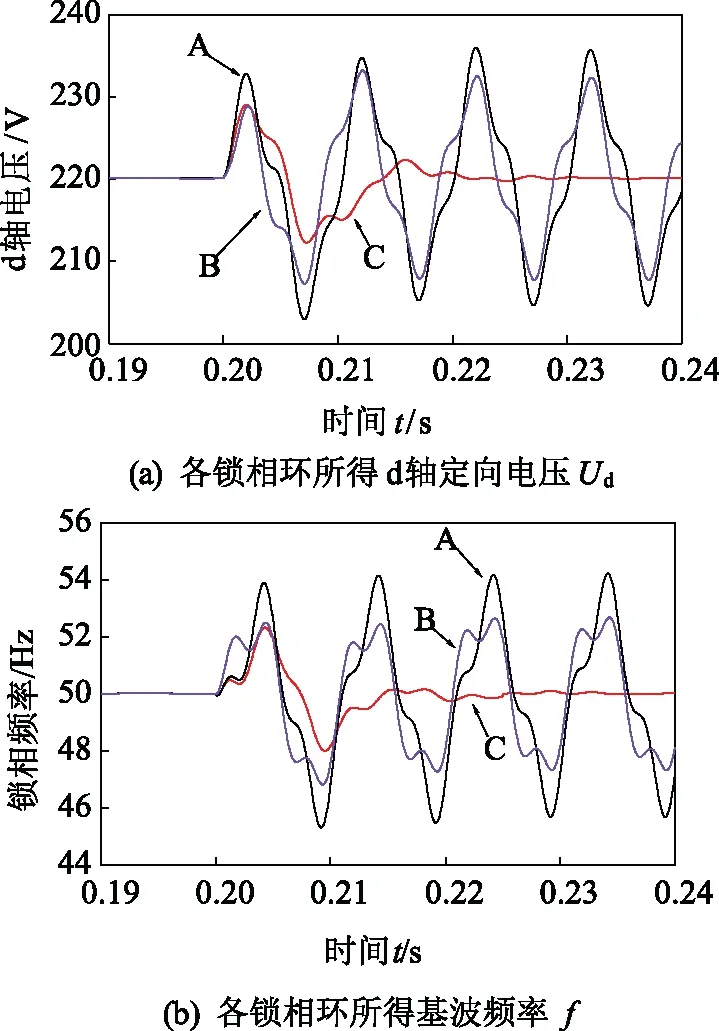
图9 条件3下仿真结果Fig.9 Simulation results in case 3
综上,利用所设计的改进型SOGI,通过对其进行扩展应用,可以很好地避免直流分量以及低次谐波分量对锁相的影响。
5 结束语
针对传统三相不平衡锁相环存在直流分量降低锁相环检测准确度和抗低次谐波干扰能力弱的两个问题展开研究,提出一种改进型SOGI来滤除直流分量,并以其为基础进行拓展来增强系统对于低次谐波的抗扰能力,并通过仿真验证了本文所提锁相方案的有效性。
