基于激光测距的管壳件圆柱度测量系统

柴 众， 陆永华， 陈 强， 高 铖

(1. 南京航空航天大学 机电学院， 江苏 南京 210016； 2. 国营锦江机械厂， 四川 成都 610043)

0 引 言

圆柱度是机械零件形状误差的一种， 是指实际圆柱面要素对其理想圆柱面的变动量. 圆柱度的公差带是两同轴圆柱面间的区域， 该两同轴圆柱的半径差即为圆柱度公差值. 圆柱度对于轴类零件和孔类零件的装配起到重要作用. 圆柱度误差太大不仅影响零件的互换性， 还会影响整个工件的质量， 降低工件的使用寿命[1]. 所以， 研究零件圆柱度的快速、 准确测量具有重要的意义.

目前， 传统的回转零件的圆柱度误差以接触式测量为主， 主要有3种测量方法： 两点法或者3点法、 圆柱度仪、 三坐标测量仪. 两点法和3点法的测量精度受人工操作影响较大； 圆柱度仪检测圆度误差、 圆柱度误差时需用精密回转台带动工件回转检测[2]； 三坐标测量仪的价格昂贵， 并且检测步骤复杂， 测量时间较长， 只适合于小批量的精密零件测量[3]. 对于尺寸较大或较小、 形状复杂的零件的圆柱度， 通过传统的接触式测量方法更是难以实现. 与传统的接触式测量方法相比， 基于传感器的非接触式测量方法具有测量精度高、 测量效率高等优点. 典型的非接触式测量方法包括： 激光三角测量、 超声波测量和机器视觉测量， 广泛应用于复杂零件表面测量、 形状公差测量、 机械零件尺寸公差测量等领域[4].

在非接触测量方面， 长春理工大学的邓建男[5]基于激光共焦位移传感器， 借助旋转反射镜及轴系径跳误差计算系统， 真正减少了测量过程中的各种误差， 实现了对小孔圆度误差的精密检测； 齐鲁工业大学的张鹏等[6]设计了一套重卡桥壳专用的圆度圆柱度误差检测仪， 根据零件形貌特征设计了PLC 及伺服驱动系统控制平台， 控制激光位移传感器采集桥壳轮廓多个截面的数据， 使用最小二乘法作为误差评定标准实现圆度和圆柱度误差的测量； 吉林大学的张瑛玮[7]采用二维激光位移传感器， 通过线激光旋转扫描法， 获得被测圆柱工件内表面多个截面的二维坐标信息， 根据最小二乘法计算各截面的中心坐标， 由此拟合出一条基准轴线， 并进行同轴度误差评定； 西安交通大学的颜敏炜等[8]设计了一种基于二维激光位移传感器的同轴度检测装置， 用于检测车桥减速器桥壳轴承孔的同轴度误差； 在圆柱度计算方法方面， 浙江大学宁波理工学院的张学昌等[9]建立了基于误差转换的平面曲线和空间曲线误差数学模型， 结合圆和圆柱的数学表达建立满足最小包容条件的圆度和圆柱度误差评定数学模型， 提高了汽车曲轴轴颈圆度误差、 圆柱度误差检测效率和精度； 合肥工业大学的王标等[10]提出了一种基于5点法， 利用误差分离模型提取出圆柱截面上最小二乘圆的中心向量， 进而重构出符合数学定义的圆柱轮廓线， 用于评定圆柱度误差. 该创新技术解决了在现场测量中精确、 高精度重建圆柱轮廓的关键问题.

发动机壳体是一种常见的回转件， 主要为整个发动机承担保护和支撑作用. 但是由于其尺寸较大， 实际中不容易直接测量其圆柱度. 本文针对这一问题提出一种基于激光位移传感器的管壳件圆柱度测量方法. 根据发动机壳体的形状， 设计并实现了测量系统的机械结构和测量软件. 通过电动旋转台带动激光位移传感器在发动机壳体的某一截面旋转一周， 获得该截面的轮廓数据点. 通过直线运动模组调整激光位移传感器的上下高度， 测量壳体的不同截面. 建立零件的空间坐标系， 将测量得到的多个截面数据点转化为空间坐标， 并投影到XOY平面上. 最后， 根据圆柱度的定义， 使用粒子群优化算法拟合得到包括所有测量截面数据点的最小区域同心圆， 计算两同心圆的半径差即为管壳件的圆柱度误差[11]. 相比于传统的测量方法， 本文提出的测量方法柔性更好、 自动化程度更高， 测量过程涉及的多个环节均由测试人员通过工控机控制， 非接触式的测量方法使其具备较高的测量精度， 极大地提高了测量效率， 节约了测量成本.

1 测量系统原理与设计

由于发动机壳体的尺寸较大， 现实中无法获取内圆柱面的轮廓， 故获取其内圆柱面几个截面的轮廓信息， 根据多个截面轮廓信息评定圆柱度.

1.1 测量系统原理

1.1.1 圆柱度评定模型

根据圆柱度的定义可知， 圆柱度的公差带是两同轴圆柱面间的区域， 该两同轴圆柱面半径差即为圆柱度误差. 反应在针对管壳件的实际测量过程中， 即为包括所有测量截面数据点的最小同心圆柱的半径差φ即为圆柱度误差. 圆柱度的评定模如图 1 所示.

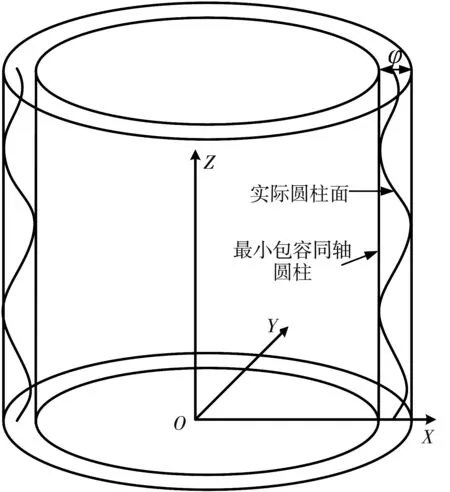
图 1 圆柱度评定模型示意图Fig.1 Schematic diagram of cylindricity evaluation model

1.1.2 建立测量系统坐标系

为了将激光位移传感器获得的距离值转化为三维坐标信息， 需要建立测量系统的坐标系. 以电动转台所在平面为XOY平面， 旋转中心点为坐标圆心O(0,0), 垂直于XOY平面向上的方向为Z轴的正方向， 根据笛卡尔坐标系的右手定则， 建立该测量系统的三维坐标系， 如图 2 所示.

图 2 测量系统坐标系

Fig.2 Coordinate system of measurement system

实际选择的直线运动电机的直线度为0.01 mm， 并且与光学平台垂直安装， 所以， 可近似认为旋转轴线与测量坐标系Z轴重合. 由于零件的表面平整， 零件的实际轴线也垂直于光学平台， 可将测量得到的数据点投影到XOY平面， 将同心圆柱的半径差距离转化为同心圆的半径差， 然后， 通过最小区域法计算得到同心圆的半径差. 即可获得零件的圆柱度误差.

1.2 测量系统设计

测量系统的硬件结构主要由电动旋转台、 直线运动模块、 激光位移传感器和其余辅助装置组成. 激光位移传感器固定在直线运动模块上， 可以随着直线运动模块上下移动， 以测量零件的不同截面. 电动旋转台带动激光位移传感器旋转1周， 获取某个待测截面的轮廓信息. 由于激光位移传感器的量程较小， 所以， 通过导轨滑块调节激光位移传感器的初始测量位置， 即可适应不同内径零件的测量， 扩大测量系统的测量范围. 最终设计的测量方案如图 3 所示.

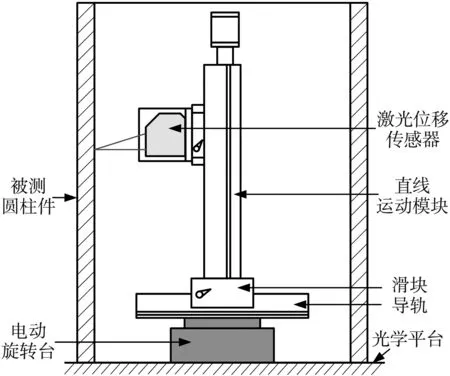
图 3 圆柱度测量系统示意图Fig.3 Schematic diagram of cylindricity measurement system

1.3 测量平台搭建

根据测量方案的原理， 选择合适的测量设备， 最终搭建的实际测量平台如图 4 所示.

图 4 测量系统试验平台Fig.4 Experimental platform of measurement system

选择德国米铱optoNCDT2300系列型号为ILD2300-50的激光位移传感器， 该激光位移传感器具有测量精度高， 使用简单等特点. 其量程为50 mm (45 mm～95 mm)， 测量频率设置为5 kHz， 绝对误差不超过10 μm.

直线运动电机用于带动传感器测量管壳件的不同截面， 获得多个测量截面的结果， 用于后续的圆柱度拟合. 选择直线电机的有效行程为250 mm， 直线度为0.01 mm， 精度为±0.02 mm.

电动旋转台带动激光位移传感器旋转1周， 测量零件某一截面， 传感器获得N个测量点， 其相对于开始位置旋转的角度与测量的数据点一一对应， 所以电动转台应具有比较高的分辨率. 选择的电动旋转台台面的平行度为15 μm， 分辨率为0.001°， 重复定位精度为0.005°.

根据传感器的测量范围， 计算测量系统的测量管壳件的半径范围为121 mm～321 mm. 测量系统中直线运动电机和电动旋转台的驱动通过上位机控制运动控制卡实现， 通过RS-422接口接收激光位移传感器的测量距离值. 整个测量系统的结构如图 5 所示.

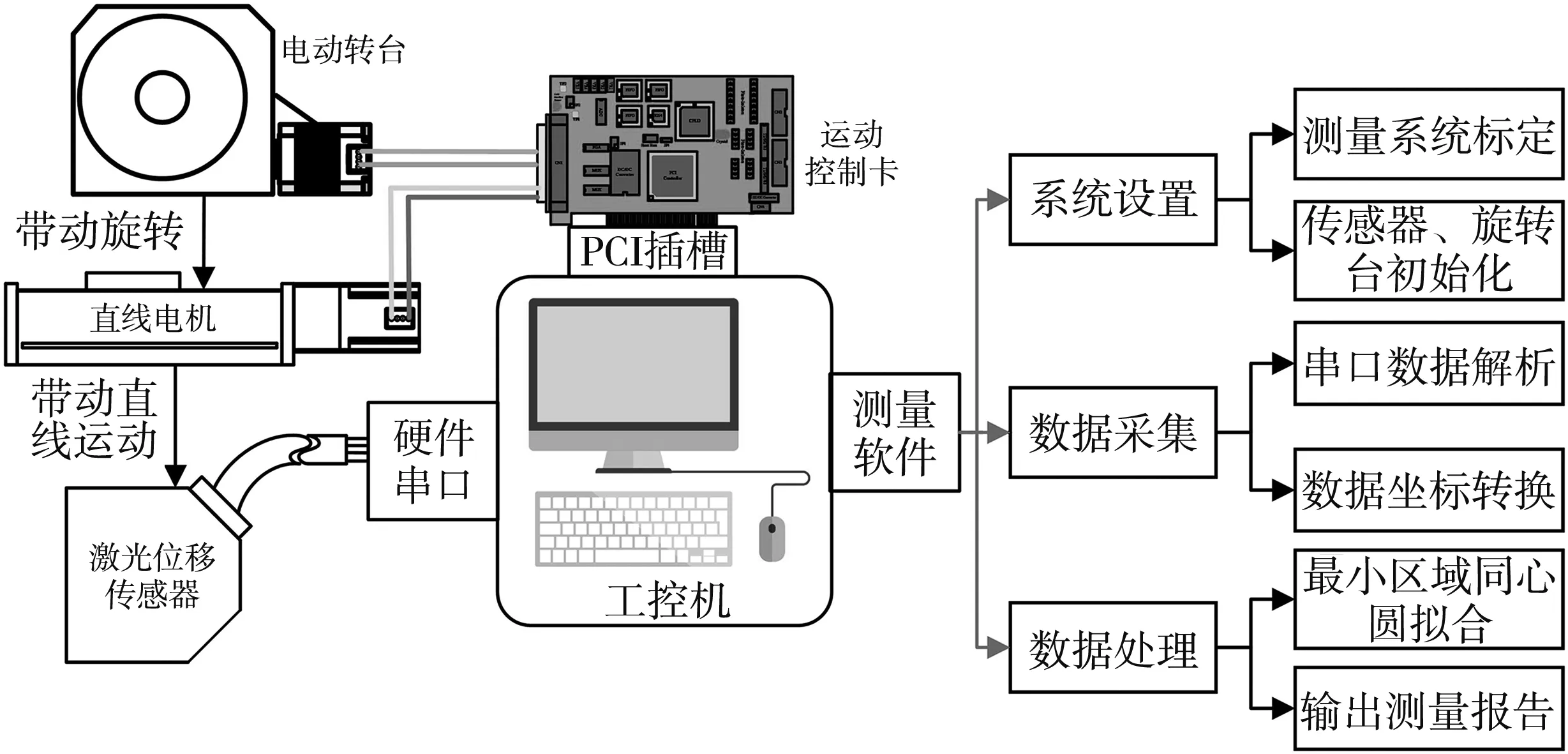
图 5 测量系统结构图

2 测量系统标定

由于实际测量过程中， 激光传感器的出射点很可能并不在旋转中心轴上， 而是有一个偏移量r0.如果需要获得测量截面的数据点到旋转中心轴的距离， 需要首先对系统进行标定， 获取激光传感器的出射点到旋转中心轴的距离值r0， 结合激光位移传感器测量的距离值ri即可得到该测量点到旋转中心轴的距离值. 标定示意图如图 6 所示.

图 6 系统标定示意图Fig.6 Schematic diagram of system calibration

用1个已知内径为R0的标准圆柱体对测量系统进行标定， 在零件旋转1圈的过程中， 传感器获得一系列距离值ri， 其中有1个最大值rimax和 1个最小值rimin. 满足式(1)

2r0+rimax+rimin=2R0.

(1)

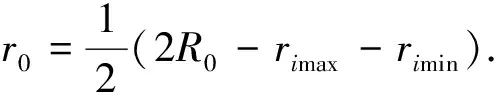
(2)

通过上述方法即可完成对测量系统的标定. 完成系统标定后， 再对待测零件某一截面进行测量， 根据传感器测量获得的一系列距离值， 再结合该测量点与起始测量点的角度即可得到该截面的轮廓信息.

3 圆柱度测量流程

完成系统标定之后即可进行圆柱度测量试验. 下面介绍圆柱度的测量流程.

3.1 截面信息获取

放置好待测量的圆柱管壳件， 电动转台的转速设为4 r/min， 传感器的采集频率设置为5 kHz， 通过上位机软件控制电动转台带着激光位移传感器测量管壳件的1周， 则每个截面可以获取80 000个测量点. 第i个测量点相对于起始测量点的角度

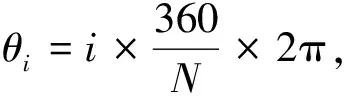
(3)

式中：θi为第i个测量点相对于起始测量点的角度；N为测量获得的数据点数.

根据每个测量点的角度值θi和每个测量点的距离值， 结合标定得到的激光出射点到旋转中心的距离r0即可计算得到每个测量点的二维坐标， 从而获得该测量截面的轮廓信息.

第i个测量点的坐标(xi,yi)为

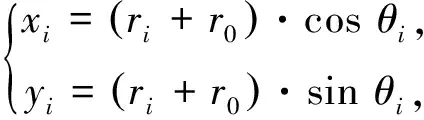
(4)

式中：ri为传感器到测量点i的距离值，i=1,2,3,…,n；θi为每个测量点相对于起始测量点的角度值；xi为测量点i的横坐标，i=1,2,3,…,n；yi为测量点i的纵坐标，i=1,2,3,…,n.

3.2 最小区域圆拟合

根据圆柱度的定义， 将所得到每个截面的测量点投影在XOY平面上， 那么， 包括所有测量点的最小区域同心圆的半径差即为该零件内径的圆柱度误差.

结合城市自然生态结构与城市发展进程中的问题进行绿道规划是发挥绿道生态保护功能的重要前提。临安地处杭州西部，城市境内三面环山，境内有青山湖和苕溪等五大水系，是典型的浙北山区城市，具有特殊的城市自然生态基底。

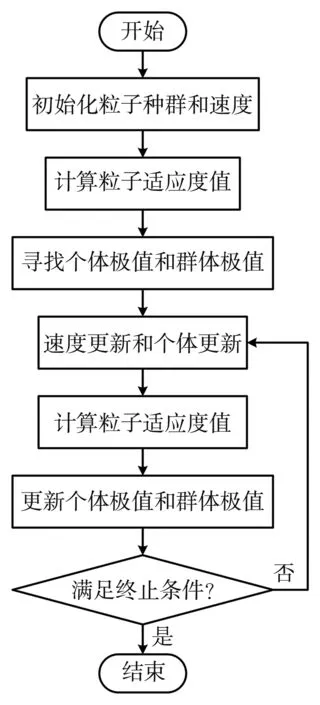
图 7 粒子群算法流程图Fig.7 Flowchart of particle swarm optimization

由于最小区域同心圆的求解过程比较复杂， 没有直接能够求解的公式， 本文采用智能优化算法中的粒子群算法对所得到的测量点进行最小区域同心圆拟合[12]. 粒子群算法是优化问题的求解方法之一， 通过不断迭代寻优得到最优解. PSO算法在非线性优化问题中是一种非常有效的优化算法， 而且PSO算法易于实现， 可调整的参数少[13]， 本文对于最小区域同心圆的粒子群算法求解的流程如图 7 所示.

其中每个粒子位置值的坐标为(xj,yj)， 则该粒子的适应度函数f(xj,yj)如式(5)所示

f(x0,y0)=

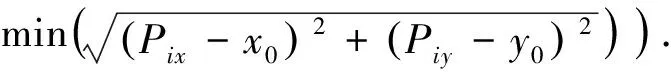
(5)

式中：Pix为测量点Pi的横坐标，i=1,2,3,…,n；Piy为测量点Pi的纵坐标，i=1,2,3,…,n；x0为最小区域同心圆圆心横坐标；y0为最小区域同心圆圆心纵坐标.

在获得多个截面的圆心坐标和半径后， 将式(5) 作为圆心求解的目标优化函数， 使用粒子群算法迭代求解过程中， 各个参数的取值如表 1 所示.

表 1 粒子群算法参数取值

采集多个截面后， 将所有截面的数据投影到XOY截面， 对所有测量点使用粒子群算法进行最小区域同心圆拟合， 拟合结果如图 8 所示.

图 8 最小区域圆拟合结果Fig.8 Fitting results of minimum area circle

3.3 计算圆柱度误差

在获得最小区域圆的圆心之后， 最小区域圆的小圆半径Rmin即为所有测量点中距离圆心最近的距离， 最小区域圆的大圆半径Rmax即为所有测量点到圆心距离最远的距离. 所以， 圆柱度误差φ=Rmax-Rmin.

根据上述的数据， 最小区域圆小圆的半径为140.140 mm， 大圆的半径为139.854 mm， 所以， 圆柱度误差为0.286 mm.

4 测量系统试验与分析

在测量试验之前， 需要先对测量系统进行系统标定. 标定完成之后对同1个待测零件重复做 8组试验， 每组试验利用上文中的圆柱度评定方法获得其圆柱度误差.

4.1 系统标定试验

使用精度较高的标准件对该测量系统进行标定试验， 标准圆柱内径的标准值为280 mm， 为避免标定过程中产生随机误差， 选择该零件的 6个截面进行标定试验， 每个截面之间相距10 mm. 根据式(2)， 将得到的6组标定结果取平均值， 最终计算的结果作为激光出射位置到转台旋转中心的距离r0. 标定试验的结果如表 2 所示.

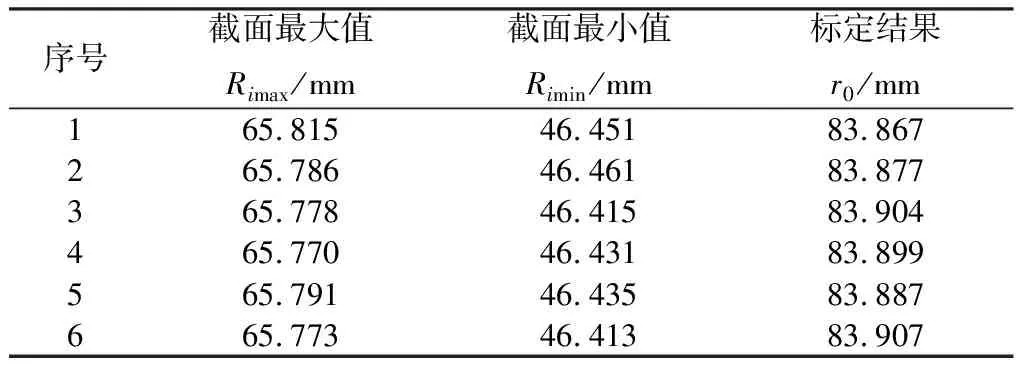
表 2 系统标定试验数据

6组标定结果的极差为0.04 mm， 标定结果的重复性较高. 对6组标定结果求取平均值得到最终的标定结果r0=83.890 mm. 完成系统标定后， 即可进行圆柱度测量试验.

4.2 圆柱度测量试验

换上发动机壳体进行圆柱度测量试验， 使用本文提出的测量和数据处理方法对同一待测零件进行8组测量试验， 每组试验测量发动机壳体的 8个截面， 所得到的圆柱度误差如表 3 所示.

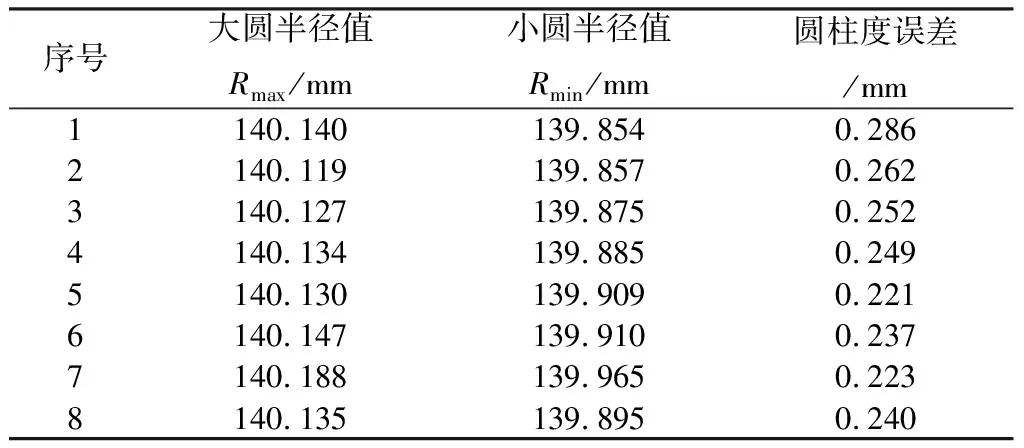
表 3 圆柱度测量试验数据

根据表 3 的测量结果绘制圆柱度误差变化曲线， 如图 9 所示. 试验结果表明， 测量系统点额稳定性较好， 8组测量结果的极差为0.065 mm.

图 9 圆柱度误差试验结果Fig.9 Experimental results of cylindricity error

4.3 测量系统不确定度

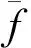
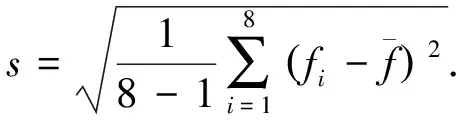
(6)

4.4 试验误差分析

1) 测量设备带来的误差

激光位移传感器本身的测量值存在10 μm的测量误差， 由传感器的制造精度决定；

2) 数据处理方法带来的误差

使用粒子群算法求解最小区域圆时， 由于各粒子的初始值具有随机性， 因此， 每一组数据的圆心拟合结果也存在少许差异， 导致圆柱度误差计算结果存在差异.

3) 测量方案带来的误差

试验中认为旋转中心轴与光学平台垂直， 并且被测零件的轴线也与光学平台垂直. 其实设备和零件存在制造误差和装配误差， 实际中并不垂直， 这对测量结果也会带来影响.

5 结束语

本文设计并搭建了一种基于激光测距的管壳件圆柱度非接触式测量系统， 并开发了相应的上位机测量软件， 通过上位机软件控制调节激光位移传感器的测量位置， 实现整个测量过程. 本文设计并实现的测量系统对于管壳件的圆柱度误差具有较好的测量效果. 试验结果表明， 该测量系统具有较高的测量精度和测量效率. 测量系统的不确定度为0.021 mm， 对同1个零件进行8组测量， 重复测量误差不超过0.065 mm. 单个零件圆柱度的测量时间在5 min之内， 能够实现管壳件圆柱度的快速、 准确测量.