基于综合难度系数模型的数学高考试题比较研究*

2022-02-16佛山科学技术学院528000李静依洪锐敏

中学数学研究(广东) 2022年24期

佛山科学技术学院(528000) 李静依洪锐敏

华南师范大学(510631) 彭上观

1 问题提出

2014 年9 月国务院发布《关于深化考试招生制度改革的实施意见》,随着全国高考试点改革工作的推进,浙江、上海等16 省市相继开始实行新高考政策,取消文理分科.对于数学学科来说,传统高考模式采用文理分科的形式,理科数学卷的难度高于文科数学卷,而新高考政策与传统高考模式的区别在于不再区分文理科,同时试题增加了多选题与结构不良试题等新题型.

难度是反映试题质量的重要指标之一,2019 年《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》强调科学设置试题难度[1].广东省等作为第三批新高考改革的试点省份,2021 年高考数学开始采用新高考I 卷,从使用全国高考I 卷到新高考I 卷,试题难度有什么变化? 目前国内学者对执行新高考政策前后的高考数学试题综合难度的纵向比较研究相对较少.因此,本文确定以下研究问题: (1)广东等省份执行数学新高考前后试题的综合难度是否有明显差异? (2)实施新高考后数学试题的难度因素变化趋势如何?

2 综合难度系数模型

Nohara 在2001 年提出了总体难度的概念,其中涉及“问题拓展”、“实际背景”、“运算水平”及“推理过程”4 个难度因素,这是综合难度系数模型的研究雏形[2].鲍建生在其基础上提出了数学课程的综合难度模型,即“探究”、“背景”、“运算”、“推理”、“知识含量”的5 维度模型[3].对于应用于高考的标准化考试试题,更加强调试题的区分度和层次性,武小鹏为了让难度模型更加贴合高考试题的综合难度模型,在鲍建生的5 维度模型基础上增加了“思维方向”和“是否含参”2 个维度[4],并基于AHP 理论构建了数学高考试题综合难度模型[5].李保臻和石烨认为一道数学解答题涉及多个小问题,不同的小问题之间有的单独成立,有的互相关联,呈现出层层递进的梯度形式;针对解答题,李保臻等在武小鹏的7 维度模型基础上增加了“梯度”因素,提出了基于高考试题的8 维度综合难度模型[6].从试题综合难度模型的发展史来看,以上各试题综合难度模型一脉相承并日趋完善.其中,武小鹏的数学高考试题综合难度模型较为全面地囊括了各难度因素并借助层次分析法有效地说明了各难度因素的权重,因此本研究主要以武小鹏的数学高考试题综合难度模型[5]为理论支撑,并关注李保臻等提出的“梯度”因素对试题综合难度的影响.具体模型界定见表1.

各难度因素的难度系数di计算公式参考鲍建生在5 维度模型中给出的难度系数di公式[3],即

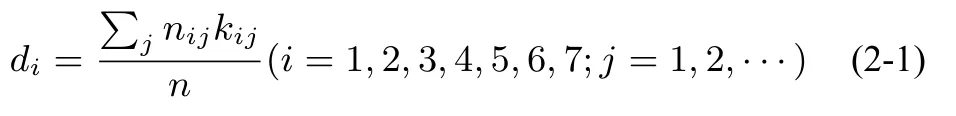
其中,kij为第i个难度因素的第j个水平所占的权重,nij为第i个难度因素的第j个水平所涉及的题目数量,n为该份高考试题的题目总数量.通过取各难度因素的难度系数的加权平均值即可得整份高考试题的综合难度D,即

其中,ki为各难度因素在整份高考试题中所占的权重均值系数.

对于不同难度因素的权重ki和同一因素中不同水平的权重系数kij,采用武小鹏等学者依据绝大多数专家及一线教师倾向性评分的方式,结合层次分析法确定的权重系数,ki=(0.40,1.20,0.83,2.50,0.40,0.83,0.83),kij见表1[5].

表1 综合难度系数模型界定

3 研究设计

3.1 研究对象

本研究以广东等省份执行数学新高考改革前后的2020年“全国高考I 卷(理科)”(下称“2020 年高考理科I 卷”)、2021 年“全国新高考I 卷”(下称“2021 年新高考I 卷”) 和2022 年“全国新高考I 卷”(下称“2022 年新高考I 卷”)作为研究对象,对这3 套试题的综合难度建立模型并进行比较研究,从而定量分析数学高考试题难度的变化.

3.2 数据处理

本研究以武小鹏的数学高考试题综合难度模型[5]为理论支撑,采用结合编码的主题定性文本分析法进行编码分析,编码示例如下:

例2(2022 年新高考I 卷第17 题)记Sn为数列{an}的前n项和,已知a1=1,是公差为的等差数列.(1)求{an}的通项公式;(2)证明:.

该题编码为“无背景A1”、“有参数B2”(存在参数n,项目处于动态变化中)、“简单符号运算C3”(运算涉及到简单符号的推导)、“复杂推理D2”(推理涉及3 步以上推导),“大于等于三个知识点E3”(涉及等差数列定义、数列递推公式、累乘法求数列通项、裂项求和及不等式证明等知识点)、“顺向思维F1”(问题解决符合数学思维的特点,由已知推向未知,顺向直接解决问题)、“运用水平G2”(综合运用上述知识点解决问题).

按照表1 难度因素的内涵界定,由两名研究者对三套试题进行双盲编码,编码一致性为89.74%,再对不一致的编码项进行讨论.统计不同难度因素不同水平的题目数量和占比情况,并按照公式(2-1)(2-2)和计算各难度因素的难度系数di和整份高考试题的综合难度D,结果见表2.

4 研究结果

4.1 实施新高考后数学试题综合难度逐年递增

由表2 可得,广东等省份实施新高考后数学试题综合难度逐年递增,2020 年高考理科I 卷的试题综合难度系数D=6.70,2021、2022 年新高考I 卷试题综合难度系数分别为7.14 和7.70,新高考I 卷的试题综合难度更高.

表2 近3 年数学高考I 卷试题难度系数统计表

为了直观地比较出这3 份高考试题难度之间的差异,下面作出各难度因素的综合难度系数雷达图,如图1 所示.这3 份高考试题的考查侧重点大体走向一致,在实施新高考改革前后,3 套试题在“背景因素”、“是否含参”、“思维方向”三个难度因素的考查相差不大,但新高考I 卷在“运算水平”、“推理能力”、“知识含量”、“认知水平”这4 项难度系数有了较大提升;且与2021 年新高考I 卷相比,2022 年试题在这4 方面的难度系数也有显著提升.下面针对这4 个难度因素进行具体分析.

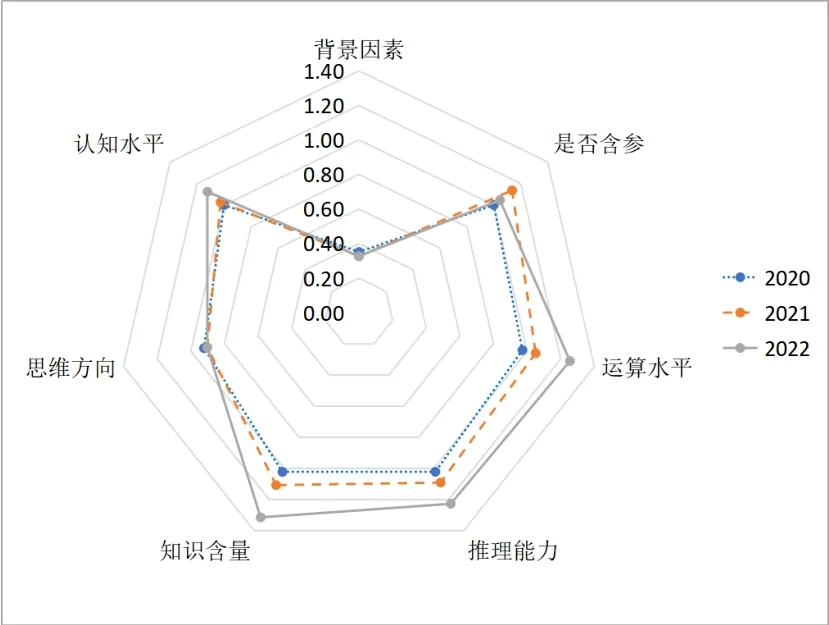
图1

4.2 不同难度因素变化趋势分析

从“运算水平”维度上分析,2020 年高考理科I 卷、2021和2022 年新高考I 卷的难度系数分别为0.97、1.05 和1.25.其中复杂符号运算占运算因素的权重最大,如图2,2021 年和2022 年新高考I 卷含复杂符号运算的题目百分比分别为27.27%和36.36%,而2020 年高考理科I 卷含复杂符号运算的题目百分比为26.09%,说明新高考试题更加重视对复杂符号运算题目的考查,要求学生在数学学习过程中要夯实数学运算基本功,特别要加强对于含有复杂符号运算的数学问题解题训练,提升解题的速度.

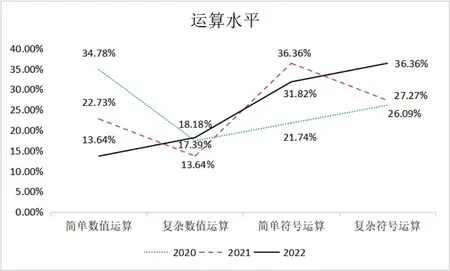
图2

从“推理能力”维度上分析,2020 年高考理科I 卷、2021和2022 年新高考I 卷的难度系数分别为1.02、1.09 和1.23.如图3,2021 年和2022 年新高考I 卷推理步数多于三步的题目百分比分别为59.09%和72.73%,而2020 年高考理科I 卷推理步数多于三步的题目百分比为52.17%,说明新高考试题在经历2021 年新高考I 卷的过渡之后,2022 年更强调对考生的复杂逻辑推理能力的考查,学生在平时的练习过程中要加强对演绎推理和归纳、类比推理能力的锻炼.

图3

从“知识含量”维度上分析,2020 年高考理科I 卷、2021和2022 年新高考I 卷的难度系数分别为1.02、1.11 和1.31.如图4,2021 年和2022 年新高考I 卷含三个及以上知识点的题目百分比分别为36.36%和54.55%,而2020 年高考理科I卷含三个及以上知识点的题目百分比为30.43%,说明新高考试题更加重视对三个及以上知识点题目的考查,要求学生要有过硬的数学学科综合能力,以便于解决多知识点交叉的问题.

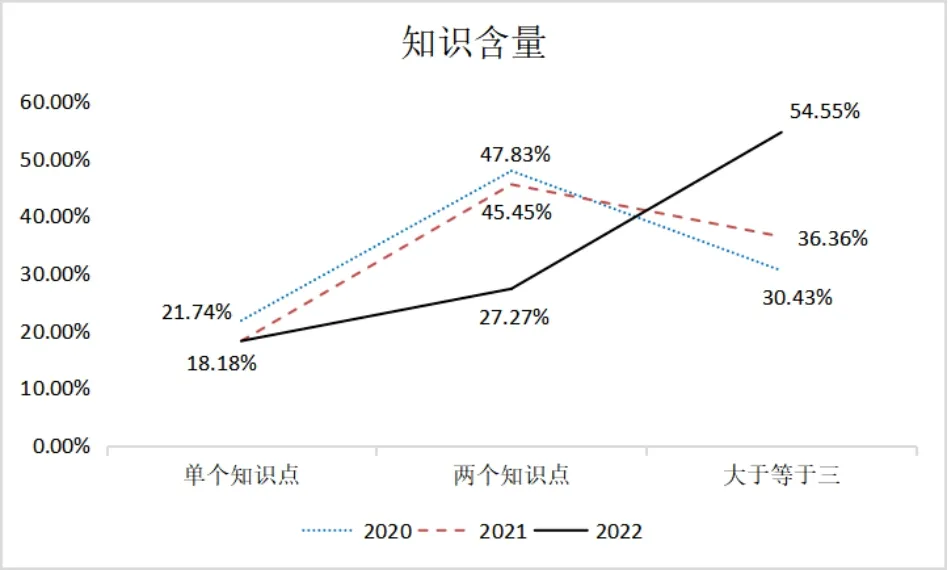
图4

从“认知水平”维度上分析,2020 年高考理科I 卷、2021和2022 年新高考I 卷的难度系数分别为1.00、1.03 和1.12.根据综合难度系数模型,理解、运用和分析的权重分别为0.33、0.96 和1.71,三份高考试题在“分析”水平的题目考查占比相差不大,但在“运用”水平的题目考查占比相差较为明显,结合“运用”和“分析”两个水平,如图5,2021 和2022 新高考I 卷在深度认知水平的题目考查占比分别为72.73%和77.27%,高于2020 年高考理科I 卷的题目考查占比69.57%.新高考试题更强调对考生深度认知水平的考查,要求学生从基本概念和定义出发,深挖题目的已知条件,建立合适的数学模型,并对模型进行优化,进而解决问题.

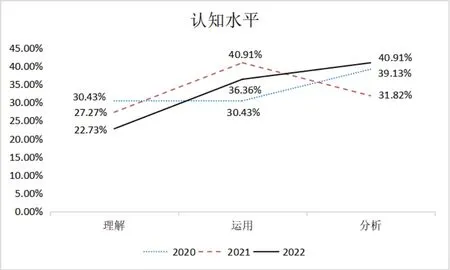
图5

此外,结合李保臻等人提出的“梯度”因素进行对比分析,2021 年和2022 年新高考I 卷试题中各小问题之间有关联的解答题百分比分别为100%和83.3%,而2020 年高考理科I 卷该部分题目的百分比为71.43%,说明新高考试题对解答题各小题的设置更强调其逻辑性和层次性,往往前一个问题的答案是解决后一个问题的必要条件,在日常教学过程中教师可有针对性地根据教学实际设计出问题间有联系的试题.

5 教学建议

5.1 重视提高数学运算能力,培养学生的逻辑推理素养

教师要重视提高学生的数学运算能力,结合李保臻等人提出的“梯度”因素,教师在解题教学中应强调对复杂符号运算问题的解题训练和形成解决各小问题之间有关联的解答题的解题思路.其次,教师在教学活动中要帮助学生加强对演绎推理和归纳、类比推理能力的锻炼,重视发现和提出问题,分析和解决问题能力的过程,提高学生的逻辑推理素养[7].