角平分线性质定理的巧妙应用*——以2015年全国高考理科卷II数学第17题为例

甘肃省酒泉第四中学(735000) 徐玉庆

在2011 年义务教育数学课程标准提出了初中学生应该具备几何直观的数学素养[1],利用图形描述和分析问题,把复杂问题转化为简明、形象的几何问题.高中数学课程改革也提出了高中生应该具备的数学核心素养,提高学生应用问题和创新问题的能力[2],角平分线的性质定理,人教版在八年级上册数学第十二章“全等三角形”的第三节,而北师大版则在八年级下册数学第一章“三角形的证明”的第四节[3].定理的证明过程都应用了三角形全等.在教学和实践过程中,教师则经常强调如果在题目中出现角平分线,那么应该想到应用角平分线的性质定理,而在应用的过程中经常需要作辅助线.

1 问题的提出和解析

(2015 全国高考理科卷II 第17题) 如图1: 在三角形ABC中,D是BC边上的点,AD平方∠BAC,ΔABD的面积是ΔADC的两倍.

图1

解析这道题目如果让高中生去做,学生都想到可能要应用正弦定理,那么如何将ΔABD的面积是ΔADC的两倍这个条件嵌入到正弦定理是解决这个问题的关键,在实际应用中,许多学生并没有做任何辅助线解决了问题,解题过程如下:

分析本题巧妙的利用了三角形的面积公式和正弦定理,通过SΔABD=2SΔADC这个等量关系,寻找到了之间的关系,充分的利用了三角形的边角之间的关系,通过计算我们还可以得到一个非常重要的结论,如下:

2 问题的进一步探究

如果上面这道题目变成是一道中考题,学生是否能够解决? 问题的设计是否超出初中学生的认知水平? 是否有新的思路和方法解决该问题? 值得我们研究,笔者将这道题目给九年级的学生去做,结果让人欣喜若狂,过程如下:

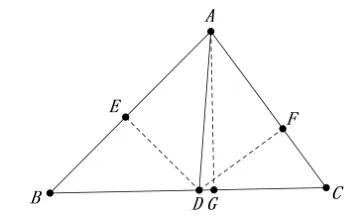
图2

分析这道高考题我们成功利用初中所学的知识得到了解决,同样我们得到了AB·DC=AC ·BD这个重要的结论,在初中几何中,当遇到角平分线,学生首先想到的是角平分线的性质定理,所以首先作AB和AC的垂线,在初中应用三角函数时一般是在直角三角形中,而垂线的构造也为三角函数的应用铺平了道路,一切都显得水到渠成,我们应用角平分线的性质定理成功的解决了这道高考题,相比之下用角平分线的性质定理解决要显得更加简洁清楚,我们用下位的概念和定理解决了更高水平的问题,这为我们解决问题提供了一种思路和方法,下位的概念和定理可以作为一种工具,在复杂问题的解决过程中,可以建立理论和研究对象之间的关系,从而建构解决复杂问题的途径.

3 结论的应用

通过上面的讨论,利用角平分的性质定理可以得到一个非常重要的定理,如图3 所示,利用该定理可以很快的解决一些较复杂的问题.(定理)在ΔABC中,AD是∠BAC的角平分线,那么AB·DC=AC·BD

图3

图4

分析这道题是2011 年全国高考理科数学卷II 的一道填空题,分值为5 分.在解决该问题的过程中,我们非常巧妙的应用了根据角平分线的性质定理所得到的结论,从而降低了这道填空题的难度,也为考生节省了许多时间.

4 反思

张景中教育数学实验已在我校开展了两年,将三角引入平面几何,发挥三角在几何中的作用,让数学变得更容易.三角是联系几何与代数的桥梁,在教育数学实验中,我们也在不断探索,如何将《新思路数学》和现行的教材相互融合,将三角函数引入数学教学中是我们研究的重点,张景中院士从面积公式出发,从单位菱形面积出发,推理出三角形面积公式,进而推理出正弦定理,从正弦定理推理出我们常用的勾股定理,这让我们眼前一亮.正如李尚志院士所说,我们不应该看规定如何,我们应该相信规律和推理,2021 年最新《义务教育数学课程标准》中加强了对初中生推理能力的要求,这也让我们对于教学数学实验有个更大的信心,借此契机让教育数学成为推动数学教育的强大动力.