深入剖析拓展 变式引领提升——2021年山东东营数学中考压轴题的认识与拓展

山东省东营市胜利第一初级中学(257000) 李 荣

2021 年山东东营数学中考延续2020 年中考模式,依然把几何图形变换综合题作为压轴题.本题重点要考察全等三角形的判定与性质,直角三角形斜边中线的性质,等边三角形的判定与性质以及锐角三角函数.突破本题的关键是要合理添加辅助线,构造三角形全等.

1 原题呈现

(2021 东营,25,12 分): 已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中距”.

(1)猜想验证如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中距”OC和OD的数量关系是____.

图1

(2)探究证明如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.

图2

(3)拓展延伸如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;

图3

②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.

2 解法分析

要证明线段相等及关系的问题,我们平时常用的方法有:三角形全等、直角三角形斜边的中线的性质、三角形中位线的性质、线段中垂线的性质,以及平行线分线段成比例等.

如图1,第一问比较容易,证明ΔAOC∽=ΔBOD,易证得OC=OD,学生容易得分,本文不再赘述,下面重点用几种方法来分析一下本题第二问和第三问.

2.1 第二问

这一问的重点需要作出辅助线,构造三角形全等,难度中等.

2.1.1 解法一

如图2-1,延长CO交BD于E,先由AC⊥l,BD⊥l,可证AC//BD,由AAS或ASA,容易证得ΔAOC∽=ΔBOE,得到CO=EO,即O为CE的中点,所以在RtΔCDE中,由斜边的中线等于斜边的一半,可得OD==OC,即OC=OD.

图2-1

2.1.2 解法二

如图2-2,延长DO交AC延长线于F,同解法一,由AAS或ASA,可证ΔAOF∽=ΔBOD,可得DO=FO,在RtΔCDF中,由斜边的中线等于斜边的一半,可得OC=OD.

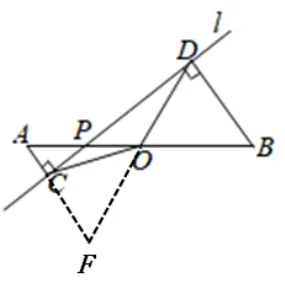
图2-2

2.1.3 解法三

如图2-3,过O作EF//CD,交BD于F,交AC于E,(可证四边形CDFE为矩形),可得OE⊥AC,OF⊥BD,又因为O为AB的中点,由前面的结论,可得OE=OF(也可以由全等证得),然后再由SAS,证明ΔCOE∽=ΔDOF,可得OC=OD.这种方法结合了矩形的判定与性质,以及三角形全等,来证明两条线段相等.

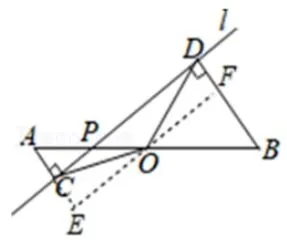
图2-3

2.2 第三问

本题最后一问,考察了三条线段之间的数量关系,需要学生用全等结合等量代换的方法,再结合锐角三角函数知识,综合性较强,要求学生能综合灵活的运用所学几何知识解决问题.

解法一如图2-4,延长CO交DB的延长线于E,先 证AC//BD,由AO=OB,先 由AAS或ASA,证ΔAOG∽=ΔBOD,可得OC=OE.在RtΔCDE中,由斜边的中线等于斜边的一半,可得OD==OC,即OC=OD.

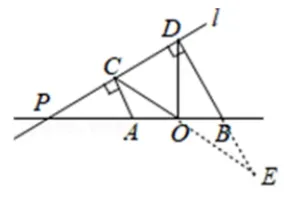
图2-4

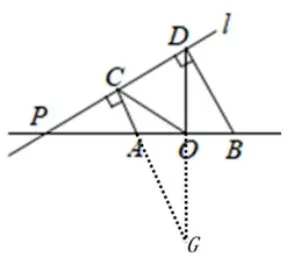
图2-5

解法二与解法一的思路相同,延长DO交CA的延长线于G,先证AC//BD,由AO=OB,先由AAS或ASA,证ΔAOG∽=ΔBOD,可得OD=OG.在RtΔCDG中,由斜边的中线等于斜边的一半,可得OC==OD,即OC=OD.

解法三如图2-6,过O作EF//l,交CA的延长线于E,交BD于F,可以证明四边形CDFE为矩形,所以OE⊥AC,OF⊥BD,又因为O为AB的中点,由第(1) 问的结论,可得OE=OF.然后再由SAS,证明ΔCOE∽=ΔDOF,可得CO=DO.这种方法结合了矩形的判定与性质以及三角形全等,同第(1)问的方法三.

图2-6

3 变式拓展

前面对本题的解法进行了详细的探讨,下面我们通过变化∠COD的度数对最后一问进行拓展研究.

3.1 变式1

拓展延伸如图3-1,①当点P是线段AB延长线上的任意一点时,“足中距”OC和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;

图3-1

②若∠COD=120°,请直接写出线段AC、BD、OC之间的数量关系.

解析①结论仍然成立,证明略.

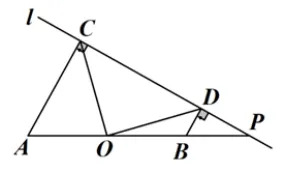
图3-3

图3-4

②结论:AC+BD=OC.理由: 如图3-2,∵∠COD=120°,OD=OC=OE,又∵∠COE=60°,∴ΔCOE是等边三角形,∴CE=OC,∵ ΔAOE∽=ΔBOD,∴AE=BD,∴AC+BD=AC+AE=CE=OC,∴AC+BD=OC.

图3-2

3.2 变式2

(3)若∠COD=90°,请直接写出线段AC、BD、OC之间的数量关系.

通过以上两个变式练习,把∠COD的度数由60°,到120°,90°,使学生对此题得解法更加熟练,理解得更加明朗,图形中三条线段的数量关系挖掘得越来越清晰.

3.3 变式3

(3)如图3-5,若∠COD=α,请直接写出线段AC、BD、OC之间的数量关系.

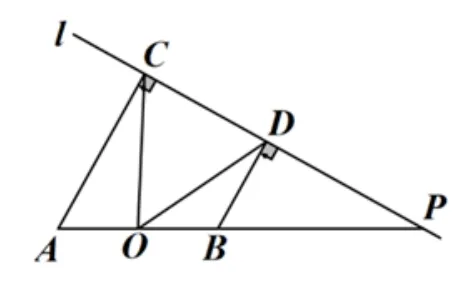
图3-5

解析结论:AC+BD=2OC ·cos.

图3-6

以上变式,对∠COD的度数在60°,120°,90°的熟练领会的基础上,由特殊到一般,锻炼了学生的总结、创新能力.也训练了学生对三角函数的应用,让学生思维得到了拓展.

4 延伸提升

4.1 变式1

如图4-1,当点P是线段AB延长线上的任意一点时,若∠COD=α,请用OC表示出四边形ABDC的面积.

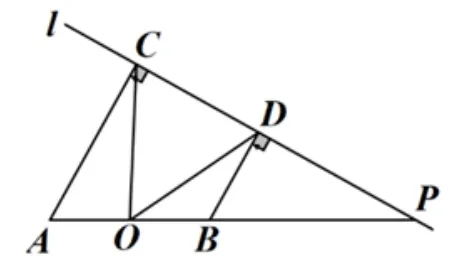
图4-1

继续引导学生发现:

延伸问题1 ΔCOD的面积与梯形ABDC有什么数量关系? 由图4-2,可得:

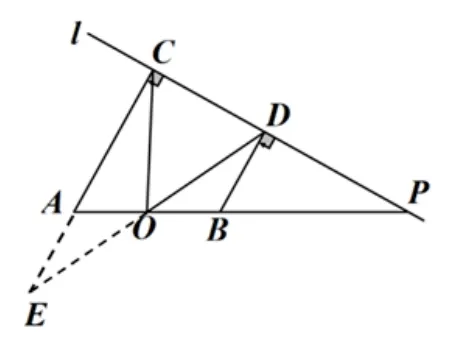
图4-2

延伸问题2 取梯形一边的中点和对边线段两个端点构成的三角形的面积始终是梯形面积的一半吗? (引导学生课后探究)

(结论: 图4-3 成立,图4-4 不成立)

图4-3

图4-4

4.2 变式2

图4-6

如图4-5,当点P是线段AB上的任意一点时,若∠COD=α,请用OC表示出ΔOCD的面积.

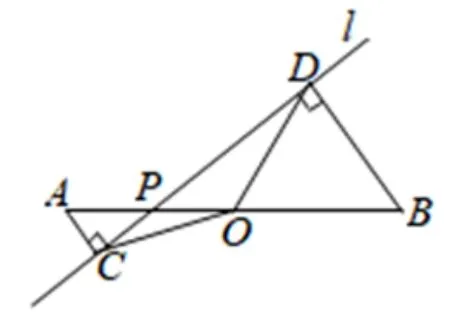
图4-5

这一环节的延伸提升,在内容上涉及到了中考中常考的与中点有关的面积问题,重点是引导学生发现规律,进而能自己证明,方法上结合全等的性质和三角函数,对学生的综合运用能力是很好的锻炼.

5 结语

中考试题是命题专家们集体智慧的结晶,作为老师,我们在平时的教学过程中,不仅仅要自己认真钻研,对中考试题进行深入探索,同时也要引导学生多进行对重点题型深入探究.如果能像上题这样进行多角度的变式练习与探究,不仅仅能达到触类旁通、举一反三的目的,还可以在这一过程中让学生体会到数学的乐趣,进而达到“一叶一树一森林”的效果.