双稳态余弦梁非线性隔振器的动力学与隔振特性研究
2022-02-16王文波李双宝
张 威, 王文波, 李双宝
(1. 中国民航大学 航空工程学院,天津 300300; 2. 中国民航航空地面特种设备研究基地,天津 300300;3. 中国民航大学 理学院,天津 300300)
针对这一问题,有学者发现并联三根正刚度弹簧得到的装置,理论上不仅具有高静载支撑能力与低动刚度特征,而且还能实现准零刚度,进而可用于低频隔振。其中,Carrella等[4-7]较早研究过具有高静低动特征的三弹簧并联隔振系统的静力学与隔振传递率特性,结果表明其具有低频隔振性能。但是,具有准零刚度特征的隔振器的设计难点在于构造负刚度。其中,横向线性弹簧并联构造的负刚度结构是最常见的形式,其负刚度原理和复杂的非线性动力学现象被Cao等[8-11]进行过深入的研究,其中Hao等[12]基于Cao等的研究,对一种用于低频地面振动测试(ground vibration test,GVT)非线性支撑系统的准零刚度振子模型的未扰系统动力学进行了研究,得到满足准零刚度的结构参数。近年来在负刚度弹性元件的构造上出现了以磁弹簧[13-14]、剪刀架结构[15]、滚轮-凸轮-弹簧机构(cam-roller-spring mechanisms,CRSM)[16]、碟形弹簧[17-18]、空气弹簧[19]、新材料构造的新结构[20-21]以及梁或杆[22-26]等。其中梁有直梁和曲梁两种,曲梁又分为两端受载屈曲梁和两端固支余弦梁。Benjamin等将两端固支屈曲梁低频隔振器用于抗冲击试验研究,得到其隔振峰值大大降低,但未对其动力学进行理论分析。王云峰等[27]基于拉格朗日原理建立了两端固支屈曲梁隔振器的动力学模型,并对其隔振性能进行了分析,结果表明其低频隔振性能优于线性系统。然而两端固支屈曲梁具有明显的缺点,即难以精确控制其预压力,从而极大限制了其在工程中的应用。
由文献[28]可知余弦梁在不需要两端施加载荷情况下就具有双稳态特性,还可通过改变拱高与梁厚得到不同的力与位移关系,以及实现负刚度等。因此,在考虑小变形的情况下,本文提出双稳态余弦梁非线性隔振器,其由两端刚性固定的余弦梁负刚度元件与垂向正刚度线性弹簧并联构成。通过分析该系统无阻尼未受扰动情况下的动力学模型,得到满足该系统准零刚度平衡点的充要条件。对其进行静力学分析,提出可以通过改变余弦梁的高厚比,进而改变系统的刚度以实现低频隔振。本文还定义了双稳态余弦梁非线性隔振器的准零刚度平衡点。通过分析双稳态余弦梁非线性隔振器的力传递率,得到了系统的起始隔振频率值。
1 双稳态余弦梁非线性隔振器的静力学分析
1.1 双稳态余弦梁
如图1所示为两端固支的双稳态余弦梁结构,其中:l为两固定端的距离;δ为梁截面厚度;H为初始时刻梁轴线中点距两端点连线的垂直距离即梁的拱高;E为弹性模量;I为惯性矩;X为压缩位移。两端固支曲梁在文献[29]中已被研究,但未给出其静力学方程。Qiu等研究了两端固支余弦梁横向受载时的回复力,得其前三阶回复力与位移关系式(1)。
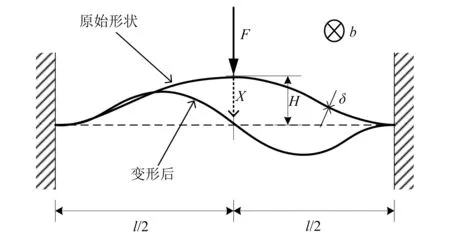
图1 双稳态余弦梁受横向载荷示意图Fig.1 The bistable cosine-shaped beam with cross force
(1)
(2)
所得无量纲的作用力Φi(i=1,2,3)与位移的关系,如图2所示。当h=1.65时,Φ1与Φ2在Δ=1处相切。本文考虑当h≤1.65时,即余弦梁受压过程中其垂向作用力与位移的关系只满足F1这种情况作为负刚度机构。其力与位移的关系式为

图2 不同高厚比下余弦梁的力-位移关系Fig.2 Several solutions of cosine-shaped beam normalized force-displacement relation
(3)
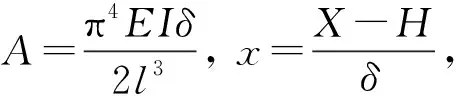
则余弦梁的无量纲力与位移关系表达式为
(4)
式(4)对x求导,则余弦梁无量纲刚度位移关系可表示为
k1=9x2-3h2+4
(5)

1.2 准零刚度隔振系统的平衡位置
余弦梁结构可以被设计成具有优异的抗冲击性能的机构,如果并联一正刚度为K1的垂向线性弹簧,理论上可以在实现高静载支撑能力的同时兼具低动刚度,同时拥有较好的低频隔振性能。本文的双稳态余弦梁非线性隔振系统结构,如图3所示。
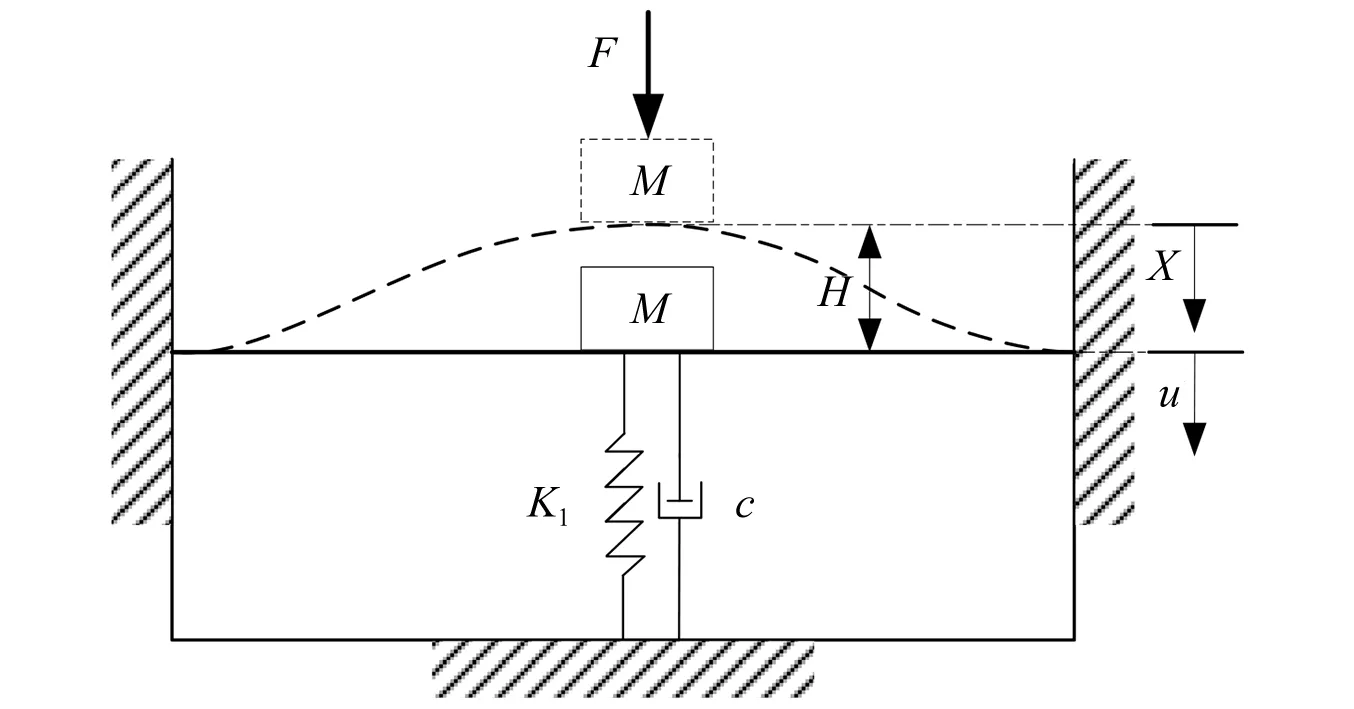
图3 双稳态余弦梁非线性隔振系统结构示意图Fig.3 Structure of nonlinear vibration isolator with bistable cosine-shaped beam
不考虑质量M和阻尼c,在轴向受载F的作用下,系统的力与位移关系可表示为
(6)
对式(6)无量纲处理,得系统的无量纲力与位移关系式为
(7)

将式(7)等式两边分别对x求导,得到隔振系统的无量纲刚度与位移关系式为
(8)
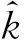
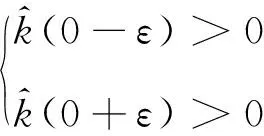
(9)
在工程实践中,隔振系统的无量纲刚度比a应大于或等于0。根据式(9),在平衡位置x=0处的等效刚度比记作a0,其与等效高厚比h的关系为
(10)
式(10)表明等效刚度比a0与高厚比h有关。将式(10)分别代入式(7)、式(8),即可得其无量纲恢复力的表达式为
(11)
无量纲刚度的表达式为
(12)
式(12)与对式(11)求关于x的一阶导数得到的刚度表达式一致。由上述定义可以得如下结论:当且仅当a=a0时,隔振系统存在唯一的稳定准零刚度平衡点x=0。
根据式(8)、式(10)现对本系统的零刚度平衡点个数作如下分析:
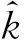
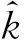
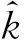
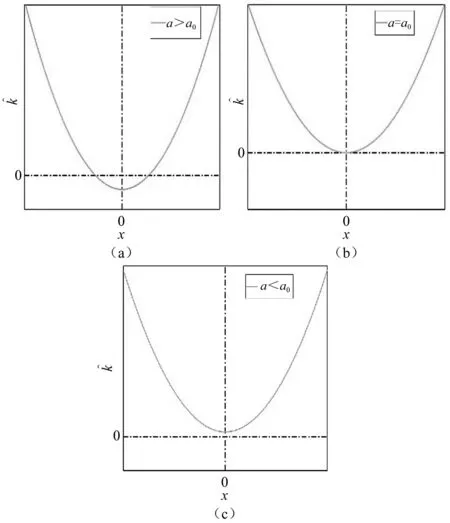
图4 不同刚度比a条件下的无量纲刚度曲线Fig.4 Dimensionless stiffness under different stiffness ratio a

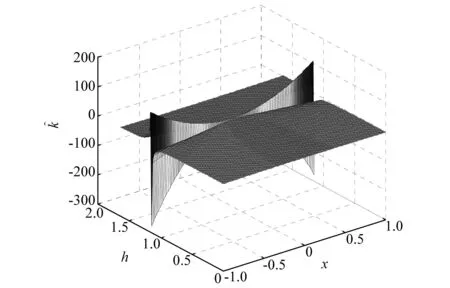
图5 刚度与位移和高厚比的关系Fig.5 The relationship among stiffness, displacement height-thickness-ratio
2 谐波激励力作用下非线性隔振器动力学模型
当双稳态余弦梁隔振系统承载质量为M的被隔振物体后,对该系统施加谐波激励力F0cos(Ωt)时,系统的动力学方程为

(13)
式(13)无量纲化后得
(14)

3 余弦梁非线性隔振器动力学分析
3.1 未扰动方程
在不考虑阻尼和外激励情况下,余弦梁非线性隔振器的未扰动无量纲动力学微分方程可表示为
(15)
将式(15)改写成一阶控制方程
(16)
令非线性恢复力为
F(x,α,β)=αx+ρx3+β
(17)
其对应的势能函数及Hamiltonian函数分别为
(18)
(19)
3.2 平衡点分岔
本节先建立双参数分岔图来揭示该系统的解在参数空间中分布的拓扑结构。根据系统式(16)可通过空间曲面表示其平衡点。由1.2节分析可知刚度比a≥0,所以有ρ≥0,又因ρ的取值不会改变平衡点的位置,为了便于分析,故可令ρ=3。这一取值也与第4章的几何参数对应的响应分析结果相同。
式(16)、式(17)即可表示成
(20)
F(x,α,β)=αx+3x3+β
(21)
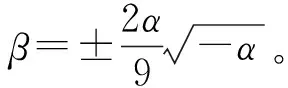
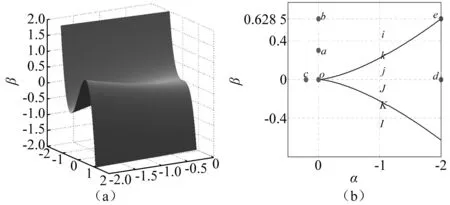
图6 系统式(20)的平衡点与静态分岔图Fig.6 The equilibrium surfacein space and static bifurcation diagram of the system (20)

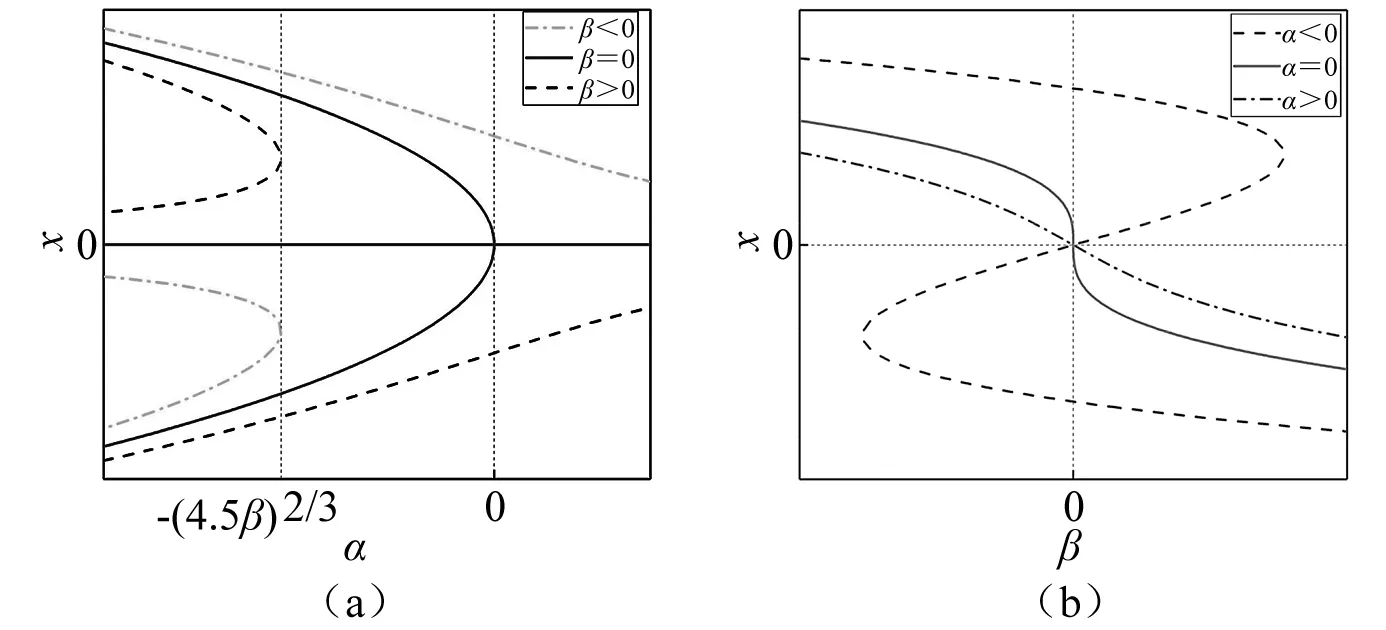
图7 系统式(20)平衡点与两个参数α,β的关系Fig.7 The relationship between equilibria of system (20) and two parameters α,β
以上相平面图8显示了系统式(20)依赖一个参数α的连续变化的转迁动力学行为。当α<0时,系统除了表现出与杜芬方程相似的标准双阱动力学行为,同时表现出类鞍点和类同宿轨道等非标准的动力学行为。当α≥0时,系统主要表现为单阱动力学行为。事实上从图9(b)中也可以直接得出系统式(20)是一个具有转迁动力学的系统即从双势能阱向单势能阱转化,点划线表示α<0系统具有双势能阱;实线、虚线分别表示α=0或α>0时,系统具有单势能阱。

图8 系统式(20)的代表性相图以及平衡点Fig.8 Representative phase portraits and equilibria of the system (20)
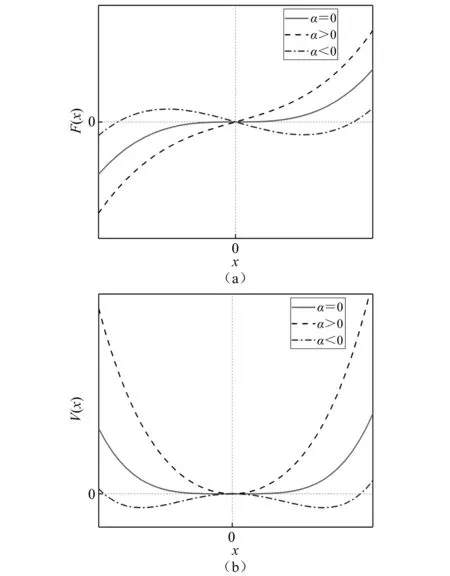
图9 参数α对非线性恢复力、势能的影响Fig.9 Effect of parameter α on nonlinear restoring force and potential energy
通过本节的研究还可以得到系统式(20)的存在稳定的零刚度平衡点的条件为α=0,β=0。根据非线性恢复力式(21)对位移x求一阶导数得其非线性刚度为
K(x)=α+9x2
(22)
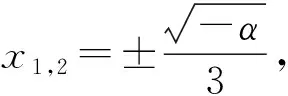
由相平面图8的分析可知β=0系统才具有对称性,当α取值从0~-2的过程系统式(20)具有转迁行为,只有当(α,β)=(0,0)时系统才有稳定的零刚度平衡点即(α,β)=(0,0)是系统具有准零刚度平衡点的充要条件。
3.3 系统隔振动力学响应与周期解的稳定性分析
如图3所示,考虑到该系统为单自由度非线性隔振系统且受谐波力激励F0cos(Ωt)作用时,当其承载一定质量为M的物体后,系统正好处于平衡位置u=0处,此时系统的刚度为零。其黏性阻尼为c。根据式(7)和式(10)可得承载质量M与系统参数之间的关系为
(23)
隔振系统运动微分方程可以写成
(24)
式中:u=X-H;Fr为谐波力激励下系统的恢复力。
由式(11)和式(23)可得
(25)
因此,式(24)的无量纲形式为
(26)
其中,几何参数比为
(27)
考虑到无量纲微分方程,假设其具有谐波形式的周期解。运用平均法求解无量纲运动微分方程式(26)。
设
x=Acos(wt+θ)
(28)
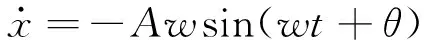
(29)
考虑对式(28)、式(29)中的A,θ求导,且令φ=wt+θ。得
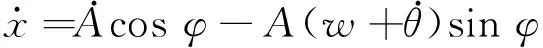
(30)
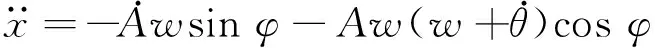
(31)
分别将式(28)与式(30)联立;将式(28)、式(29)及式(31)代入式(26)中得慢变的幅值和相位角方程
(32)
其中,
I=2Awζsinφ+Aw2cosφ-ρA3cos3φ+fcos(φ-θ)
对式(32)关于φ从0~2π积分取平均得到关于A和θ的平均方程
(33)

(34)
其对应于隔振系统的稳态解,由式(34)可得一阶近似解下的幅频响应关系式
(35)
为了确定解式(28)、式(29)的稳定性,引入扰动变量ξ=A-A0,η=θ-θ0,并将其代入式(34),令
得到
(36)
设式(36)的解为ξ=ξ0est,η=η0est,可得式(36)的特征方程
其中,
(37)
根据李雅普诺夫一次近似稳定性理论[30],如果ε1>0,ε2>0,则是奇点(A0,θ0)渐进稳定的充分条件。ε2<0,则奇点(A0,θ0)不稳定,因此ε2=0是稳定与不稳定区域的分界线。
4 系统各参数下的幅频响应

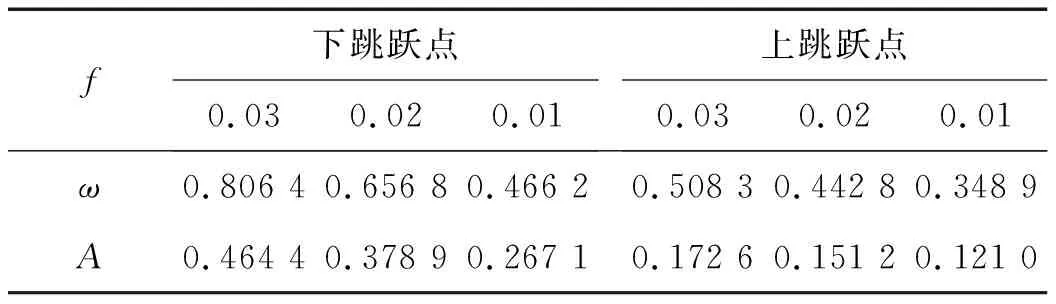
表1 各激励幅值下的上、下跳跃点Tab.1 Jump-down and jump-up points under excitation amplitude

图10 几何参数ρ与高厚比h的关系Fig.10 Relationship between geometric parameters ρ and height-thickness-ratio h
根据式(35)分析系统各参数包括阻尼系数ζ、激励幅值f、几何参数比ρ,对系统的幅频响应的影响如图11~图13所示。

图11 不同几何参数比ρ下系统幅频响应Fig.11 Amplitude-frequency responses of system with different geometric parameters ρ
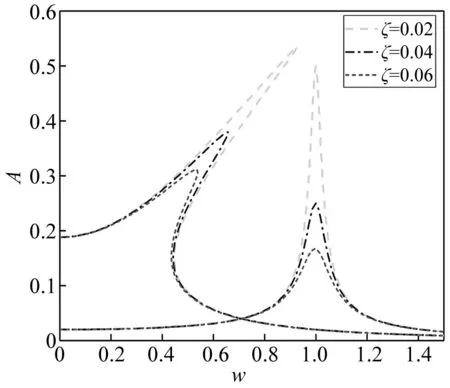
图12 不同阻尼系数ζ下系统幅频响应Fig.12 Amplitude-frequency responses of system with different damp ratio ζ
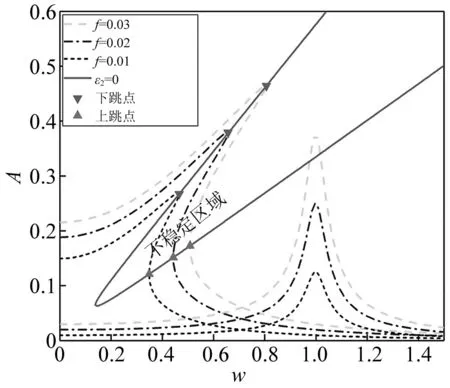
图13 不同激励幅值f下系统幅频响应Fig.13 Amplitude-frequency responses of system with different excitation amplitude f
设定参数ζ=0.02,f=0.02,可得几何配置比对系统响应的影响见图11,其中给出了不同几何配置比ρ值对应的幅频响应曲线和线性弹簧隔振系统的响应。在频率比小于1的范围内,随着几何参数比的增加共振幅值会降低同时共振频率也会增大。所以当ζ=0.02,f=0.02时,使发生向下跳跃的频率低,同时兼顾共振峰值小,故几何配置比ρ约为3。图12与图13显示了阻尼系数和激励幅值对幅频响应的影响,由图可知:当阻尼系数ζ的越大,系统的共振响应越小;反之当阻尼系数ζ的越小,系统的共振响应越大。但阻尼既不能无限增大也不能无限减小。当激励幅值f的减小,余弦梁隔振器幅值的响应也减小;当激励幅值f的增大,余弦梁隔振器幅值的响应也增大。在取相同参数值得情况下,非线性隔振器的共振响应峰值都要比线性隔振器的大。
5 各参数对系统力传递率的影响
由线性隔振系统力传递率的定义:传到基础的力与激励力幅值之比称作线性系统的力传递率。非线性隔振系统与线性系统的定义应当类似,所以屈曲梁隔振系统在激励力作用下的传递率公式为
(38)
其中,式(38)的分子为传到基础上的最大作用力包括阻尼与弹性力两部分,分母为外激励幅值。该公式与线性隔振系统传递率公式的定义类似。
根据式(26)可知,传递到基础的作用力关于无量纲位移x单调递增,因此可以得出传递率近似公式为
(39)
图14~图16分别反映了不同系统参数对非线性隔振系统力传递率的影响并与等效线性系统的力传递率的对比。由图14可得随阻尼系数ζ的增大,无论线性系统还是非线性系统的传递率随频率增加,在低频段峰值均减小在高频段力传递率增加隔振效率变差。图15反映了随几何参数ρ的增大,非线性隔振系统的共振峰值略有增加,起始隔振频率越来越大。随频率的增大不同几何参数下非线性系统的传递率最终趋近于相等,但远低于线性系统的传递率。图16反映了随外激励幅值f增加,力传递率的共振峰值也相应增加,其对应的共振频率也增加;频率增加到一定值后系统力传递率的大小也近似相等,外激励幅值越小起始隔振频率也越小。从上述三图的隔振传递率曲线均反映非线性系统隔离低频振动相比线性系统具有优越性。

图14 阻尼系数ζ对应的力传递率Fig.14 Effect of different damp ratio ζ on the force transmissibility

图15 几何参数ρ对应的力传递率Fig.15 Effect of geometric parameters ρ on the force transmissibility

图16 外激励幅值f下系统的力传递率Fig.16 Effect of excitation amplitude f on the force transmissibility

表2 力传递率对应各参数下的起始隔振频率Tab.2 Initial isolation frequency of force transmissibility under various parameters
6 隔振系统仿真分析
根据隔振系统的需要,初步设计余弦梁的结构参数长l=350 mm,宽b=32.66 mm,拱高h=4.083 mm,梁厚δ=2.887 mm,弹性模量E=168.9 GPa,泊松比σ=0.22。通过有限元软件对其静力学进行分析得其力与位移的关系与数值公式计算的结果如图17所示,仿真结果与理论计算几乎一致。
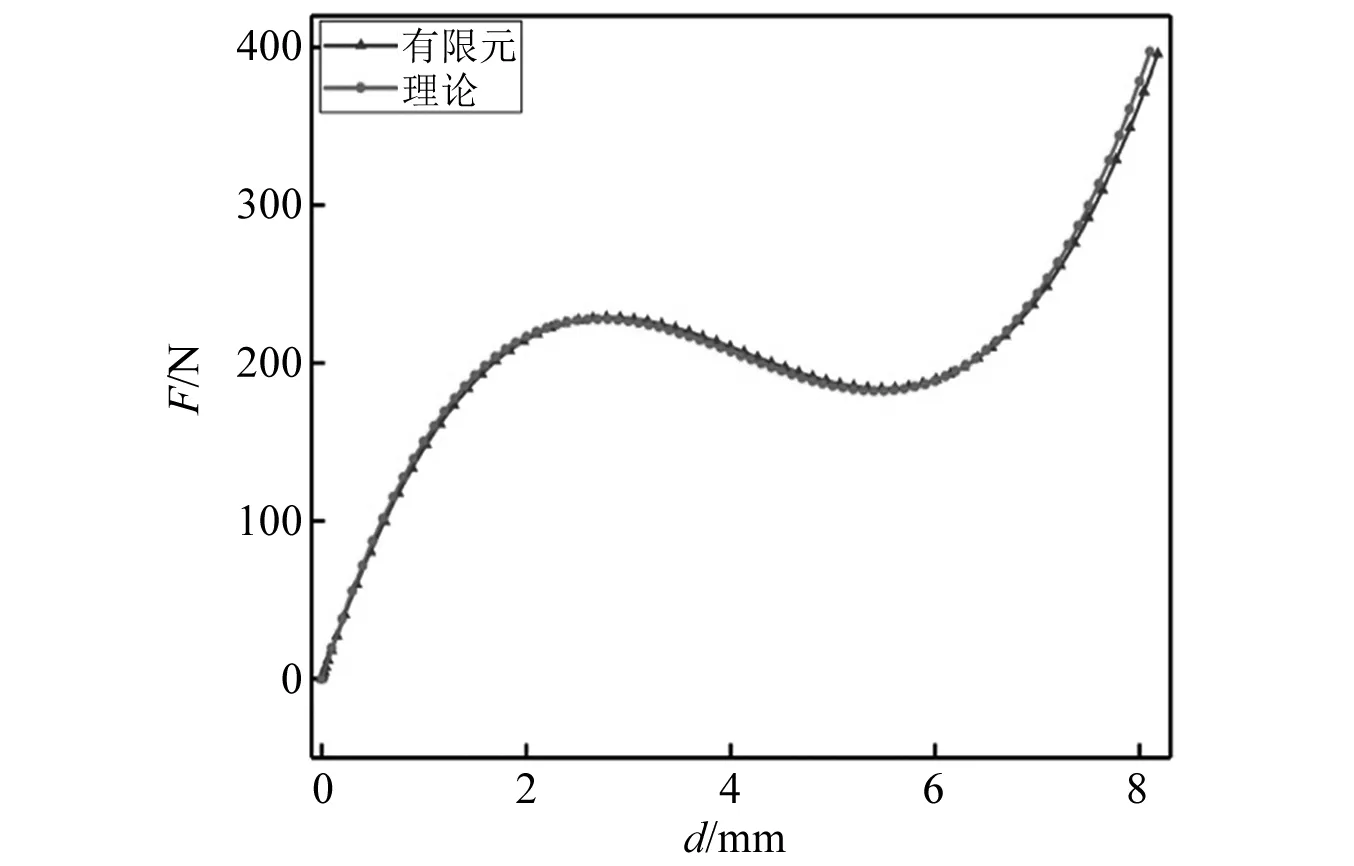
图17 余弦梁的力与位移关系曲线Fig.17 The force-displacement relation of cosine-shaped beam
双稳态余弦梁非线性隔振系统的有限元模型如图18所示,设置被隔振质量为31.7 kg,线性弹簧刚度为25.43 N/mm,阻尼比值为0.03。在有限元分析模型中通过两个分析步来实现仿真分析:第一步通过施加静力使余弦梁非线性隔振器处于平衡位置;第二步施加一个Y轴方向且幅值为15的周期性的余弦激励,通过传递到基础的力时程响应均方根值与输出激励的值相比即为余弦梁非线性隔振器的力传递率。图19显示4 s内激励频率为10 Hz时的输入、输出时域数据,其传递率为2.26,同理可得其他激励频率下的传递率值。在频率范围0~50 Hz内余弦梁非线性隔振器与线性隔振器的隔振传递率,如图20所示,仿真结果表明:余弦梁非线性隔振系统的起始隔振频率12 Hz小于线性隔振系统的起始隔振频率40 Hz,验证了本文设计的余弦梁非线性隔振器的隔振性能优于线性隔振器。

图18 余弦梁非线性隔振器有限元模型Fig.18 The FEA model of cosine-shaped beam nonlinear isolator
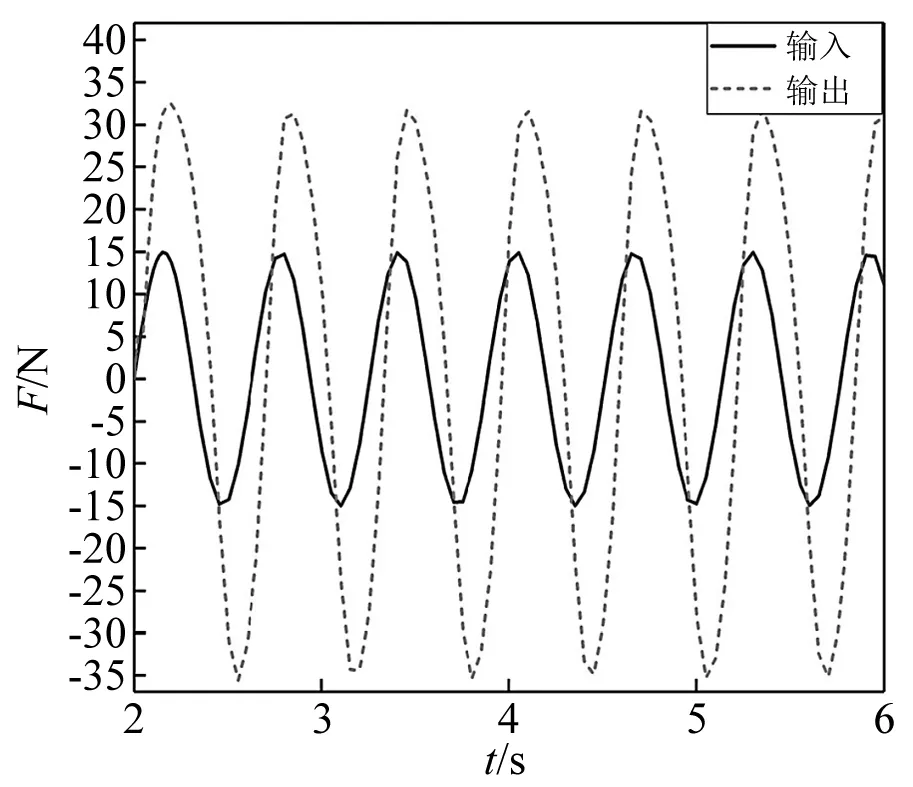
图19 激励频率10 Hz下的时程曲线Fig.19 The time curve of excitation frequency at 10 Hz

图20 有限元仿真结果Fig.20 The result of FEA simulation
7 结 论

