高速列车车下惯容悬吊设备动态特性研究

王 勇， 李昊轩， 姜文安， 汪若尘， 李 勇

(1.江苏大学 汽车工程研究院，江苏 镇江 212013； 2.江苏大学 土木工程和力学学院，江苏 镇江 212013)

随着高速铁路的快速发展以及人们物质文化需求的日益增长，人们对铁道运输系统的要求也随之提高。安全、舒适和快捷是高速列车运行的根本目的，人们迫切需求运行速度更快、乘坐舒适性更好和安全性更高的铁道运输系统。为了实现该目的，高速列车采用轻量化设计准则与动力分散式牵引方式[1]。轻量化设计降低了高速列车系统零件的质量，提高了车辆的运行速度，但导致车辆刚度降低，加剧了车体的弹性振动，降低了乘客的乘坐舒适性。动力分散式牵引方式将悬吊设备安装在车体下方，降低了轴质量，减少了车轮和钢轨的磨损，提高了列车服役时间和性能，但势必引起车体和悬吊设备的耦合振动。诸多学者对高速列车车体及车下悬吊设备的振动特性展开了大量研究。吴会超等[2]将车体等效成欧拉伯努利梁，建立了车体与设备垂向耦合振动模型，研究了车下设备刚性悬挂与弹性悬挂对车体振动幅频特性的影响，研究表明当车下悬吊设备采用合理的弹性悬挂参数时能够有效抑制车体的弹性振动，并提高车体的垂向弯曲频率。石怀龙等[3]将车下悬吊设备考虑成动力吸振器，分析了弹性车体与设备的耦合振动特性，通过合理选取悬吊设备结构参数，实现了车体减振的目的。在上述研究中，悬吊设备采用基于“弹簧-阻尼”元件结构的悬挂系统，而高速列车的运行平稳性与乘坐舒适性的进一步改善受到传统悬挂系统固有结构的制约，因此需要不断探究新的悬挂系统结构。

2002年Smith[4]首次提出了惯容器的概念，惯容器是一种具有两个相对自由运动端点的装置，其产生的作用力与两端的相对加速度成比例，该比例系数称为惯质系数且具有质量的纲。惯容器具有质量放大作用，能够提供比自身质量大的惯质效应，可以增加承载系统的惯性而不增加其承载质量。作为一种新型减振装置，惯容器已广泛运用于车辆悬挂系统[5-7]，建筑减振系统[8]、飞机起落架减振系统[9]、动力吸振系统[10-11]与隔振系统[12-14]，研究表明采用基于“惯容-弹簧-阻尼”的减振系统，能够有效提高系统的动态性能。

目前，将惯容器运用于高速列车已经引起了相关学者的注意，Wang等[15]首先将惯容器运用于列车悬挂系统中，通过Brunes和Bott-Duffin综合方法提出了一种“惯容-弹簧-阻尼”三元件串联的悬挂结构，改善了高速列车的乘坐舒适性及运行稳定性。孙晓强等[16]提出了几种结构较为简单的“惯容-弹簧-阻尼”悬挂系统，研究表明列车运行平稳性最大改善幅度可达25%。陈文韬等[17]建立了高速列车“惯容-弹簧-阻尼”悬挂结构垂向振动的动力学模型，分析了系统的振动响应特性以及隔振性能，研究发现当阻尼比和质量比取值合理时，隔振性能可得到最大程度提升。上述研究是将惯容器运用于高速列车二系悬挂系统，但将惯容器运用于车下悬吊设备中鲜有研究。

为探究采用惯容悬挂系统的悬吊设备对高速列车运行平稳性能的提升效果，本文将惯容器运用于高速列车车下悬吊设备，设计新型悬吊设备减振系统，建立高速列车车体及车下惯容悬吊设备刚柔耦合垂向动力学模型，采用遗传算法优化惯容悬吊设备结构参数，分析对比各悬挂系统的动态性能，为惯容器在高速列车车下悬吊设备的应用提供参考。

1 高速列车刚柔耦合垂向动力学模型

本文采用的高速列车车体及车下惯容悬吊设备刚柔耦合垂向动力学模型，如图1所示，包括车身，构架，轮对和车下悬吊系统。为了方便研究，将车下悬吊系统安装于车身中部下方，设车身为等截面的欧拉梁，构架、轮对和车下悬吊设备均为刚体。

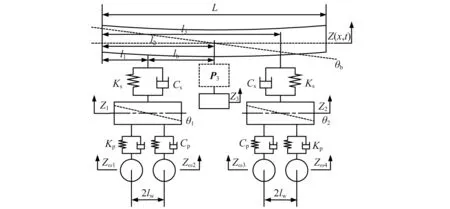
图1 高速列车刚柔耦合垂向动力学模型Fig.1 Rigid-flexible coupling vertical dynamic model of the high speed train

图1中：L为车身总长；Z(x,t)为车身垂向位移；θb为车身的点头位移；Z1，Z2和θ1，θ2分别为构架1(左)和构架2(右)的浮沉和点头位移；Z3为车下悬吊系统的浮沉位移，设轮对紧贴钢轨，其位移为轨道不平顺输入；Zω1～Zω4为第1～第4轮对的轨道不平顺垂向激励。高速列车模型参数及数值如表1所示。

表1 高速列车结构参数Tab.1 Structure parameters of high speed train

将车身简化为等截面的欧拉梁，其振动方程[18]为

i=3,4,…,n

(1)

Yi(x)=chβix+cosβix-

(2)

(3)

式中:1-chλicosλi=0;βi=λi/L;ωi和ξi分别为第i阶车体弹性振型的振动频率和阻尼比;Yi(x)和qi(t)分别为第i阶车体弹性振动的振型函数和模态坐标;l1和l2为构架1(左)和构架2(右)二系中心到车身端部的距离;l3为车下悬吊设备中心到车身端部的距离，如图1所示。P1,P2和P3分别为构架一系、二系和车下悬吊设备对弹性车身的作用力，P1,P2表示为

(4)

根据图1建立高速列车车身和构架的动力学方程

(5)

2 车下惯容悬吊设备

运行平稳性是衡量高速列车的重要性能指标之一，悬挂系统直接影响该性能指标。本文研究的高速列车车下惯容悬吊设备采用基于“惯容-弹簧-阻尼”的悬挂系统，惯容器与弹簧相连可以调节系统的惯性与刚度特性，能够改变系统的固有频率，避免系统发生共振，为了更好地实现减振，需要连接阻尼器。惯容器与阻尼器共同作用能够提高阻尼器的能量耗散效率，这种耗能增益特性首先源于惯容实现机制对等效黏滞系数的放大，其次是“惯容-弹簧”串联结构能够放大阻尼器的变形，进而提高耗能效率[19]。具备调谐机制和能量耗散增效机制的“惯容-弹簧-阻尼”系统根据元件的拓扑连接形式可以有多种结构，但惯容器与阻尼器需要在弹簧的“保护”下，才能发挥其力学性能，从排列组合角度，“惯容-弹簧-阻尼”三元件串并联减振结构共有8种形式，如图2虚线框所示。其中S0为传统悬挂系统，S2与S6结构已经有一个并联弹簧，其余6种结构还需要另外并联一个弹簧，才能用于悬挂系统，因此悬吊设备采用的惯容悬挂系统如图2所示。

图2 悬吊设备悬挂系统图Fig.2 Suspension equipment system diagram

分别建立车下悬吊设备的动力学方程

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式中:b为惯容系数;c3为阻尼系数;k3为主弹簧刚度;k31为副弹簧刚度。联立式(1)～式(14)可得

(15)

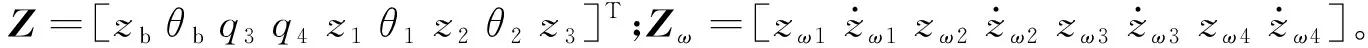
3 悬挂参数优化

3.1 优化目标

采用Sperling平稳性指标[20]来评价高速列车的运行品质，Sperling平稳性指标越小，则说明列车运行的品质越佳。因此，本文采用Sperling平稳性指标作为悬吊设备结构参数优化目标。

对于在固定轨道上运行的高速列车而言，第2～第4轮对输入可视为第1轮对的简单时延[21]，假设第一轮对不平度输入没有时延，则其对应的虚拟激励为

式中：τ1=2lw/v;τ2=2lb/v;τ3=2(lw+lb)/v。

将式(16)代入式(15)可得

(17)

(18)

则系统响应功率谱为

Syy=H(ω)*H(ω)T=Y*YT

(19)

式中,Y*和YT分别为向量Y的共轭和转置。

结合式(19)，则各采样频率点处的振幅为

(20)

式中，Δω=ωk-ωk-1为采样频率间隔。

由此可得每一频率处的平稳性指标为

(21)

式中：ak为加速度振幅;fk为振动频率;F(fk)为与振动频率相关的加权系数，可表示为

(22)

据此，可求得每一频率下的平稳性指标，然后得到全部频段下总的平稳性指标为

(23)

3.2 灵敏度分析

灵敏度分析是研究模型的状态或输出对于参数改变的敏感程度，通过对敏感参数的分析以改善模型，是工程中比较常用的方法。对悬吊设备的结构参数进行灵敏度分析，每次只改变一个参数范围，组别1、3、5、7分别代表b,c3,k3,k31基础值减小30%，组别2、4、6、8分别代表b,c3,k3,k31基础值增加30%，如表2所示，研究参数变化对列车运行平稳性的影响规律。

表2 灵敏度分析试验Tab.2 Sensitivity analysis experiment

平稳性灵敏度公式为

(24)

式中：变化前的平稳值根据基础参数模型求得；变化后的平稳值根据参数变化模型求得；平稳性灵敏度数值越大，说明变化的参数对模型影响越大；平稳性灵敏度值为正数，则说明平稳性恶化；反之，则说明平稳性提高，灵敏度分析结果如表3所示，各参数对系统平稳性影响如图3所示。

表3 平稳性灵敏度表Tab.3 Stability sensitivity table

图3 悬挂参数的平稳性敏感度Fig.3 Stability sensitivity of suspension parameters

由图3可知：S1的敏感参数为阻尼系数c3和主弹簧刚度k3;S2的敏感参数为惯质系数b、阻尼系数c3和主弹簧刚度k3;S3，S4和S5的敏感参数均为主弹簧刚度k3;S6的敏感参数为惯质系数b、阻尼系数c3和主弹簧刚度k3;S7的敏感参数为惯质系数b和主弹簧刚度k3;S8的敏感参数为惯质系数b和副弹簧刚度k31，所以选取上述结构参数(b,c3,k3和k31)为需要改进的目标参数。

3.3 遗传优化

采用MATLAB/Simulink®求得系统的动力学响应，根据式(23)求得Sperling平稳性指标作为目标函数，采用遗传算法优化系统结构参数，优化过程如图4所示，选择的优化条件如下：

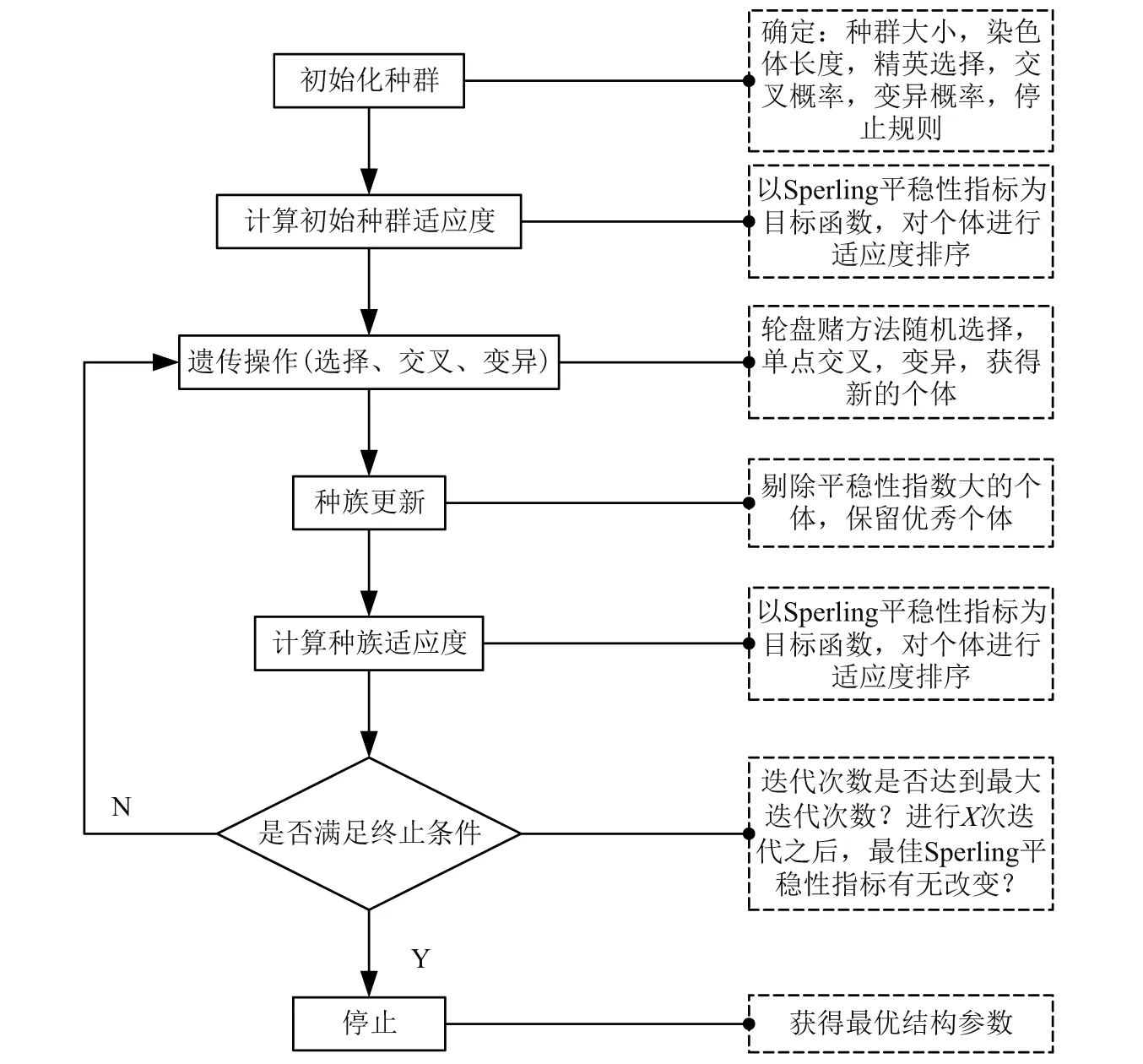
图4 悬吊设备参数优化流程Fig.4 Optimization process of suspension equipment parameters

个体数目——20；世代数——100；精英机制——选出每一代中最佳的10个个体，用于下一个种群的建立；突变——使用随机突变和自适应突变；交叉——单点交叉；选择——轮盘赌法。

考虑2个优化准则：

(1)J=min{Wtot}，

(2)悬挂系统限位行程设定为6 cm。

同时，为防止优化后得到的结构参数不符合车下悬吊设备的实际特性(如优化后得到的参数为负值或过小)，设定了相关参数的优化范围。

据此得到S0～S8悬吊设备在不同速度下的最优结构参数(b,c3，k3和k31)，优化结果如表4～表12所示。

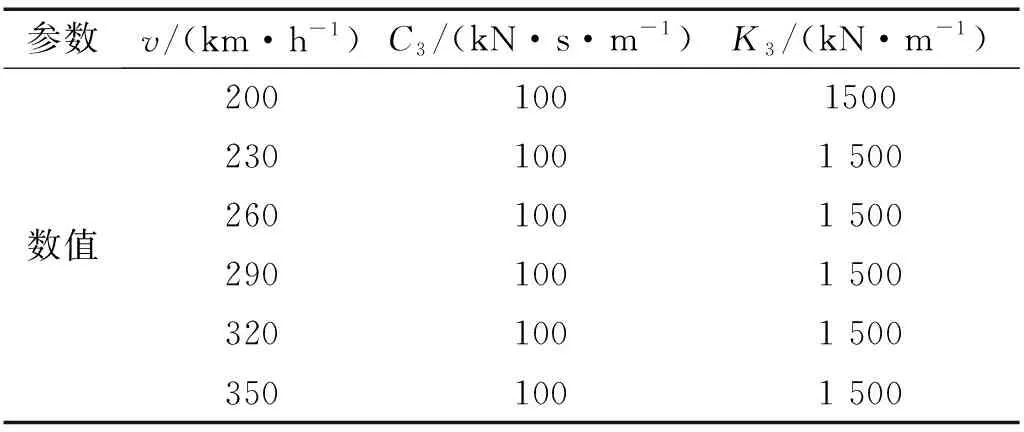
表4 S0结构参数优化结果Tab.4 Optimization results of structure parameters of S0

表5 S1结构参数优化结果Tab.5 Optimization results of structure parameters of S1

表6 S2结构参数优化结果Tab.6 Optimization results of structure parameters of S2

表7 S3结构参数优化结果Tab.7 Optimization results of structure parameters of S3

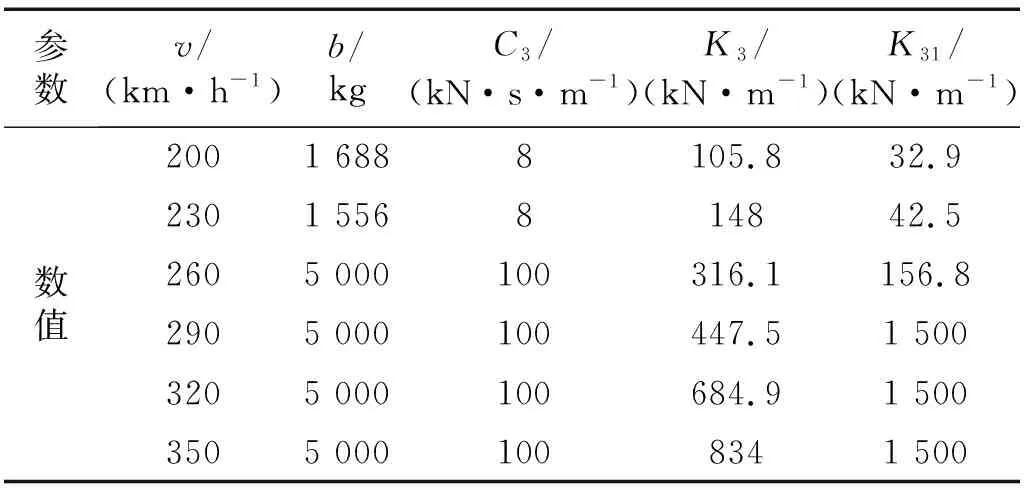
表8 S4结构参数优化结果Tab.8 Optimization results of structure parameters of S4

表9 S5结构参数优化结果Tab.9 Optimization results of structure parameters of S5

表10 S6结构参数优化结果Tab.10 Optimization results of structure parameters of S6

表11 S7结构参数优化结果Tab.11 Optimization results of structure parameters of S7

表12 S8结构参数优化结果Tab.12 Optimization results of structure parameters of S8

4 性能分析

采用典型高速列车参数，轨道谱选用高速铁路垂向位移低干扰功率谱[22]表示为

(25)

式中:Ω为空间频率；Ωc和Ωr为截断波数，分别取0.824 6 rad/m和0.020 6 rad/m；Av为表征铁道不平顺粗糙度系数，取4.032×10-7m·rad。

将式(25)所示的铁道不平顺空间频率谱进一步转换为时间频率谱

(26)

将低干扰轨道谱作为系统输入，将遗传算法优化得到的惯容悬吊设备结构参数代入系统动力学模型，求得系统的动力学响应及Sperling平稳性指标。

图5为当车速为260 km/h时，车身中部垂向振动加速度功率谱，相对于传统的“弹簧—阻尼”悬挂系统，采用惯容悬挂系统的悬吊设备在低频区均产生了抑制车身振动的作用，其中S5抑制车身振动效果显著。

图5 车身中部加速度功率谱Fig.5 PSDs of acceleration in the middle of car body

图6为在不同车速下，车身中部垂向振动位移均方根值以及其优化幅度，S2、S4、S5、S6、S8车身垂向振动位移均方根值下降程度基本一致，所以曲线基本重合。由图6(a)可知，当运行速度为200 km/h时，传统悬吊设备的车身垂向振动位移均方根值为0.085 3 m，采用惯容悬挂系统的悬吊设备的车身垂向振动位移均方根值分别为0.056 4 m,0.011 1 m,0.004 9 m,0.011 1 m,0.011 1 m,0.011 1 m,0.011 1 m和0.011 1 m，与传统悬吊设备相比，车身垂向振动位移均方根值降低了约34%，87%，94%，87%，87%，87%，87%和87%，在低速时降低了车身垂向振动位移。当运行速度为350 km/h时，传统悬吊设备的车身垂向振动位移均方根值为0.014 m，采用惯容悬挂系统的悬吊设备的车身垂向振动位移均方根值分别为0.014 9 m，0.003 6 m，0.003 6 m，0.003 6 m，0.003 6 m，0.003 6 m，0.003 6 m和0.003 6 m，与传统悬吊设备相比，车身垂向振动位移均方根值降低了约-6%，74%，74%，74%，74%，74%，74%和74%，在高速时，S1出现恶化，其余结构对减小车身垂向振动位移效果显著。由图6(b)可知，与传统悬吊设备相比，S1的车身垂向振动位移均方根值在高速时出现恶化，其余悬挂系统均减小了车身垂向振动位移，其中S2～S8车身垂向振动位移均方根值平均优化幅度最高可达87%，但S7在中低速时车身垂向振动位移均方根值优化幅度大幅下降。

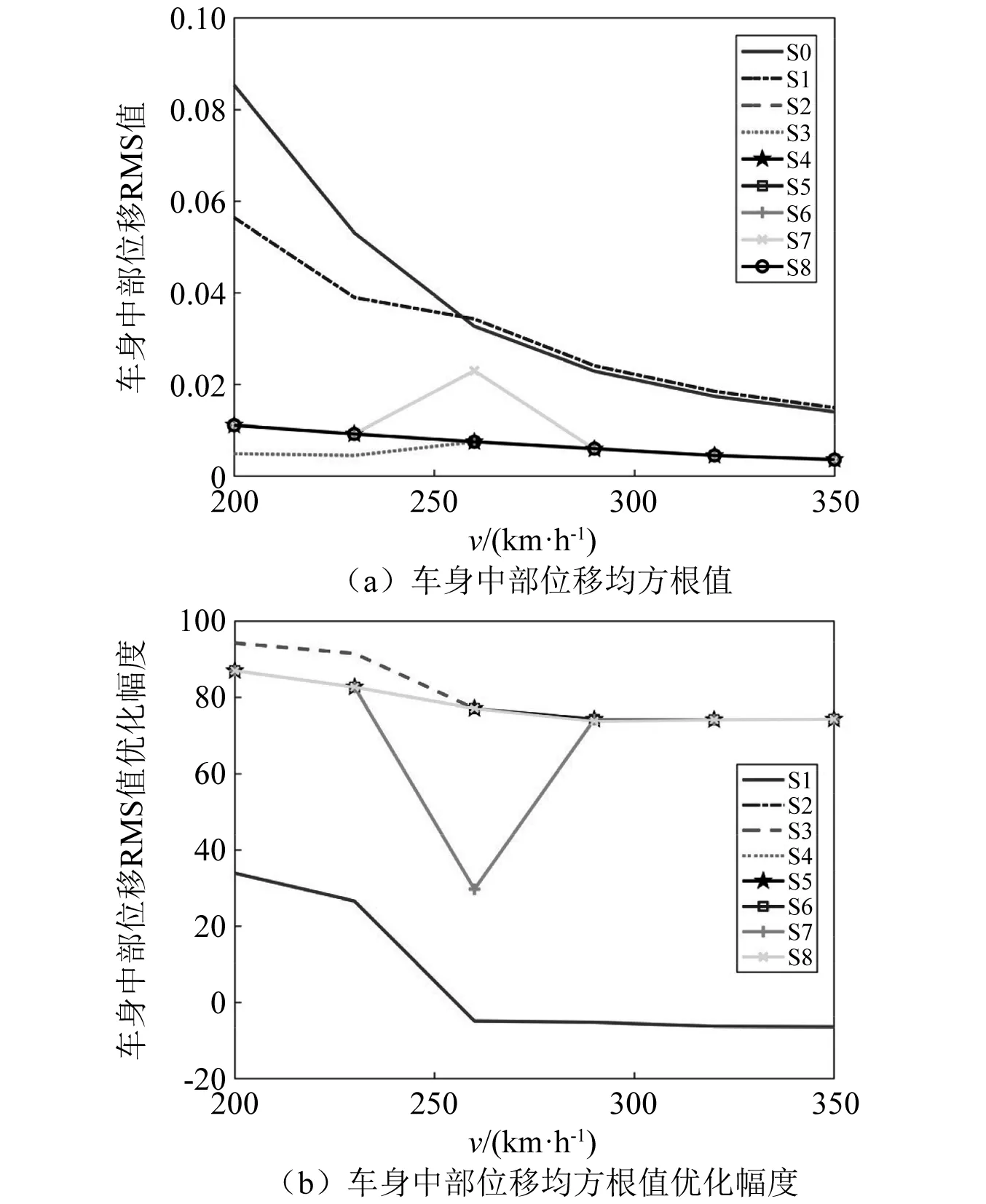
图6 车身中部位移响应Fig.6 Displacement response in the middle of the car body

图7为在不同车速下，车身中部垂向振动加速度均方根值以及其优化幅度。由图7(a)可知，随着列车运行速度的提高，车身垂向振动加速度均方根值也随之增大。当运行速度为200 km/h时，传统悬吊设备的车身垂向振动加速度均方根值为0.226 1 m/s2，采用惯容悬挂系统的悬吊设备的车身垂向振动加速度均方根值分别为0.18 m/s2，0.172 8 m/s2，0.171 3 m/s2，0.168 9 m/s2，0.114 m/s2，0.206 4 m/s2，0.126 5 m/s2和0.169 1 m/s2，与传统悬吊设备相比，车身垂向振动加速度均方根值降低了约20%，24%，24%，25%，50%，9%，44%和25%，上述8种悬挂系统均减小了车身垂向振动加速度。当运行速度为350 km/h时，传统悬吊设备的车身垂向振动加速度均方根值为0.207 6 m/s2，采用惯容悬挂系统的悬吊设备的车身垂向振动加速度均方根值分别为0.188 5 m/s2，0.182 8 m/s2，0.208 3 m/s2，0.196 7 m/s2，0.197 9 m/s2，0.212 1 m/s2，0.197 4 m/s2和0.188 m/s2，与传统悬吊设备相比，车身垂向振动加速度均方根值降低了约9.2%，7.1%，-0.3%，5.2%，4.6%，-2.2%，4.9%和9.4%，S3和S6出现轻微恶化，其余悬挂系统均能减小车身垂向振动加速度。由图7(b)可知，S5车身垂向振动加速度优化效果显著，S3，S7在中低时出现轻微恶化，S6在高速时轻微恶化，因此对于车身垂向振动加速度均方根值优化效果，惯容悬吊设备在低速时较高速更为显著。

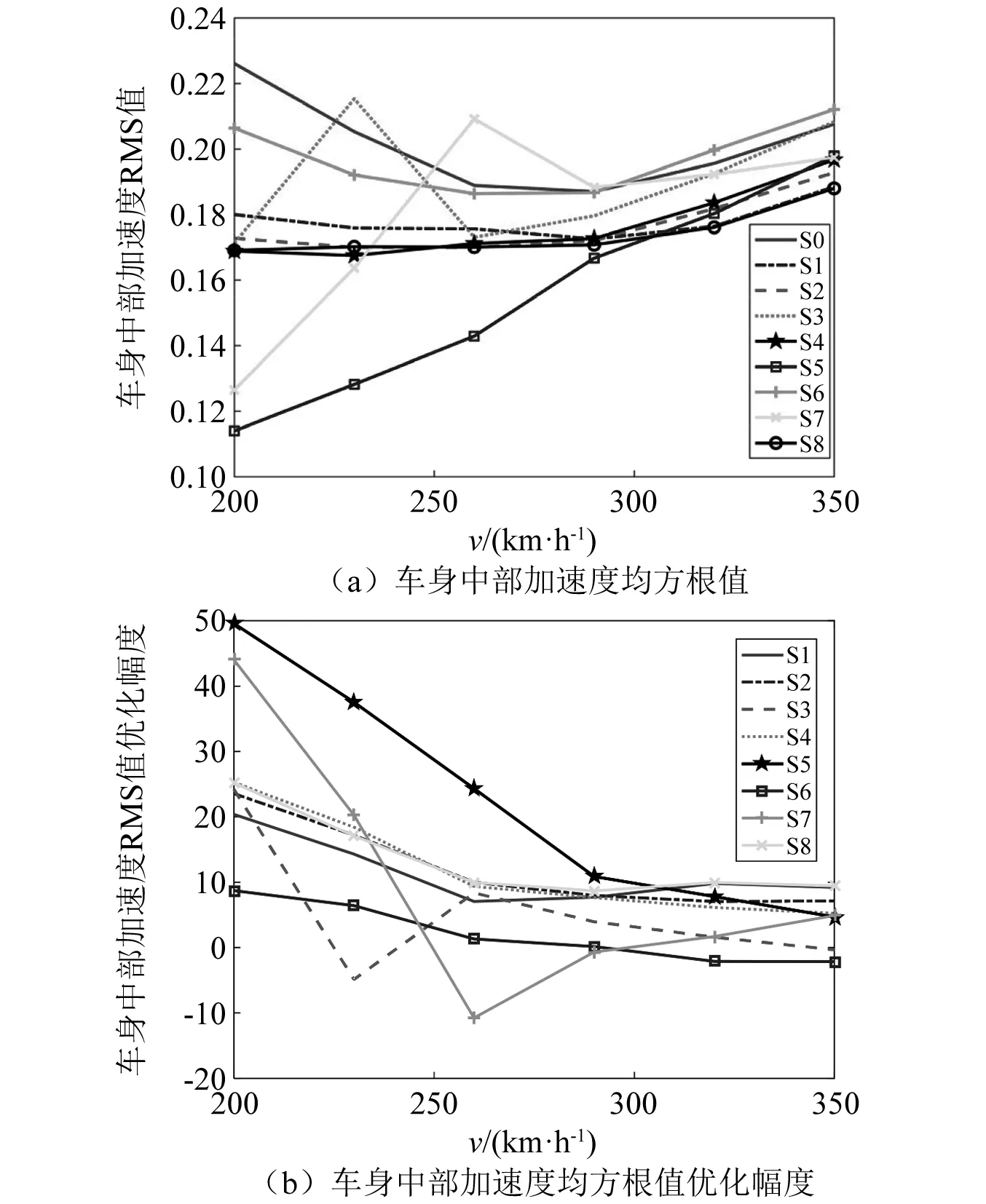
图7 车身中部加速度响应Fig.7 Acceleration response in the middle of the car body

图8及图9分别为在不同车速下，车身中部垂向振动平稳性指标以及车身中部垂向振动平稳性优化幅度。对于列车而言，将Sperling平稳性指标划分为3个等级，当其小于2.5时为优，2.5～2.75为良好，2.75～3为合格。由图8可知，随着列车运行速度的提高，Sperling平稳性指标也随之增大，但平稳性指标始终小于2.1，运行平稳性等级处于1级，运行品质优秀。当运行速度为200 km/h时，传统悬吊设备的车身垂向振动平稳性指标为1.985 9，采用惯容悬挂系统的悬吊设备的车身振动平稳性指标分别为1.833 1,1.816 9,1.791 7,1.802 2,1.678 8,1.941 4,1.707 8和1.812 6，与传统悬吊设备相比，运行平稳性指标降低了8%，9%，10%，9%，15%，2%，14%和9%，采用惯容悬挂系统的悬吊设备对列车运行平稳性提升显著。当运行速度为350 km/h时，传统悬吊设备的车身垂向振动平稳性指标为2.120 4，在采用惯容悬挂系统的悬吊设备的车身振动平稳性指标分别为2.018 2，2.051 89，2.115 1，2.071 1，2.085 3，2.127 1，2.064 2和2.013 6，与传统悬吊设备相比，运行平稳性指标降低了4.8%，3.2%，-0.3%，2.3%，1.7%，0.3%，2.7%和5%，在高速时，对列车平稳性提升效果一般。由图9可得，与传统车下悬吊设备相比，S7平稳性指标在中速时恶化，S6平稳性指标在高速时轻微恶化，其余悬挂系统的平稳性指标均得到优化，且惯容悬吊设备在低速时平稳性指标优化幅度较高速时更为明显。其中，在低速时S5平稳性指标优化幅度最为明显，最大优化幅度可达15%，其次为S4，优化幅度约为14%。

图8 Sperling平稳性指标Fig.8 Sperling index

综上，由图6～图9可得：

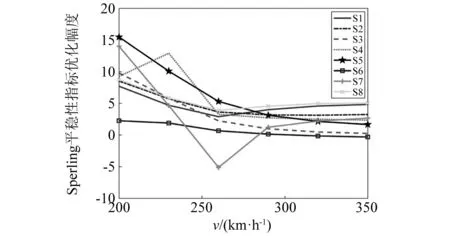
图9 Sperling平稳性优化幅度Fig.9 Optimization amplitude of Sperling index

(1)S1结构在高速时车身垂向振动位移均方根值出现轻微恶化，其余7种结构对高速列车垂向振动位移均产生了不同程度的优化；

(2) S3，S6和S7结构恶化了车身垂向振动加速度均方根值，其余几种结构对高速列车车身垂向振动加速度均产生了不同程度的优化；

(3) S7结构在中速时恶化了Sperling平稳性指标，其余7种结构对高速列车Sperling平稳性指标均产生了不同程度的优化，且在低速时优化效果更佳。

由此，8种惯容悬挂系统的选型如下：

(1)从减小高速列车车身垂向振动位移角度出发，可选取S2～S8结构；

(2)从减小高速列车车身垂向振动加速度角度出发，可选取S1，S2，S4，S5和S8结构；

(3)从提高高速列车运行平稳性角度出发，可选取S1，S2，S3，S4，S5，S6和S8结构。

5 结 论

将惯容器运用于高速列车车下悬吊设备，基于“惯容-弹簧-阻尼”三元件串并联减振结构，构建了8种惯容悬挂系统，建立了高速列车车体及车下惯容悬吊设备刚柔耦合垂向动力学模型，采用遗传算法优化得到惯容悬吊设备结构参数，通过虚拟激励法和平稳性快速算法求得系统的动力学响应，采用Sperling平稳性指标来评价系统的动态性能，对比研究了8种惯容悬挂系统的动态性能，并与传统悬吊设备进行对比分析。研究结果表明相较传统悬吊设备，惯容悬吊设备能够有效抑制高速列车车身振动，且S4，S5和S8三种结构能够有效减小车身垂向振动位移及加速度，对高速列车运行平稳性能的提升产生了明显的效果，为将惯容器运用到高速列车悬吊设备中提供参考。