沥青路面高密实度摊铺工艺参数研究

史妍妮， 刘洪海， 高新民， 杨永强， 郭宏军

(1.长安大学 道路施工技术与装备教育部重点实验室，西安 710064；2.公路建设与养护技术材料及装备交通运输行业研发中心，兰州 730030； 3.甘肃路桥建设集团有限公司，兰州 730030)

随着道路建设行业的迅速发展，道路交通基础设施建设产生的能源消耗逐渐引起了社会的关注。国际能源署发布1990年—2017年世界道路交通能源消耗的碳强度统计数据表明，2017年道路消耗碳强度达68.0 gCO2/MJ[1-3]。中国“十三五”规划中也明确指出要加快技术创新和结构调整，促进资源节约、循环高效利用。在我国，沥青路面是高等级公路的主要结构形式之一，但是在生产和施工过程中，能耗和污染较大。无论从社会发展形势还是响应国家政策上出发，都对沥青路面的施工技术、路面耐久性、使用寿命等方面提出了更高的要求[4-5]。现有的沥青路面施工过程分为搅拌、摊铺和碾压等，其中摊铺机完成混合料的摊铺后，再经过压路机的初压、复压和终压，得到一定密实度的混合料铺层[6-7]。其中摊铺机的作业参数很大程度上决定了沥青路面的摊铺质量，并且影响后续施工质量。熨平板是摊铺机的主要工作装置之一，其工作参数与路面密实度密切相关。

阿特拉斯科普柯国际亚市中心研究表明[8]，沥青路面的摊铺密实度对路面强度、耐磨性和耐久性等至关重要，同时良好的密实度分布均匀性可以降低路面建设维护费用。Sivapatham等[9]认为沥青路面的面层密实度对刚度、抗车辙性能、抗疲劳和抗低温开裂有着较大影响，提高沥青路面的密实度对路面性能有重要的影响作用。Kumar等[10-11]的研究得出了路用性能与沥青路面的压实结果密切相关的结论，通过改进压实设备和被压材料可以提高摊铺压实的质量。罗丹等[12]建立了熨平板刚柔耦合动力学模型，对熨平板的横向振幅不均匀进行了研究，提高了摊铺密实度的均匀性。刘洪海等[13]多年的研究表明，摊铺作业中沥青混合料的高密实摊铺取决于摊铺机熨平装置对被压材料的压实特性以及高密实摊铺技术的合理应用。已有研究和工程实践表明，沥青混合料经过摊铺机的整平压实，其摊铺密实度越高，投入使用后的路面耐久性越好。较高的摊铺密实度可以提高路面的质量，为后续碾压作业提供良好条件。

根据JTG F40—2004《沥青路面施工技术规范》[14]的要求，密实度为现场测量密度与试验测得马歇尔密度的比值，将实验室测的马歇尔密度做为标准密度，目标密度需达到碾压后标准密度值的96%。摊铺机对沥青混合料的压实密实度一般在80%左右，达到90%以上的称之为高密实度摊铺[15]。摊铺机完成摊铺压实后，还需压路机进行多次碾压作业以达到规范要求。过度的碾压变形会严重影响沥青路面的密实度和压实均匀性，延长沥青混合料密实成型的施工时间，降低了施工效率，增加施工成本，同时增加了沥青路面成型后早期损坏的概率[16-17]。此外，欠压实又会导致沥青路面空隙率过大，投入使用后雨水和空气易进入路面结构内部，加速路面的裂缝、唧浆和坑凼等病害的发生[18]。因此，有必要将振动理论与工程实践相结合，研究摊铺机熨平板的工艺参数，提高沥青路面的摊铺密实度，减少后续的碾压难度，获得理想的路面密实度，提高施工质量，降低能源消耗。

研究表明，机械共振的效果与施工设备和摊铺材料有关[19]，因此，要达到高密实的摊铺效果，需要对设备的工作参数和材料的特性参数进行综合研究。在已有研究基础上，基于机械共振理论建立熨平板压实机构动力学模型和密实度趋势-振动频率理论模型，并进行理论分析，获得高密实度摊铺的最佳工艺参数，最后进行现场试验，验证研究结论。

1熨平板压实系统动力学模型

1.1 压实机构动力学模型

沥青混合料的压实质量与摊铺机的工作参数密切相关[20-21]。在摊铺施工中，熨平板的振动激振器对路面产生重复激振力，具有振动加速度的颗粒会减小颗粒间的摩擦和胶结，沥青也为颗粒的运动提供了良好的条件[22-23]。当熨平板的振动频率接近系统的共振频率时，沥青混合料的颗粒会重新排列，随着接触次数的增加，颗粒变得紧密，此时沥青混合料的密实度最高。在摊铺压实过程中，熨平板的振动机构由双轴偏心质量结构组成，产生的激励F(t)作用于熨平板，如式(1)所示。

F(t)=F0eiωt

(1)

熨平板与沥青混合料相互作用的振动模型是一个非线性系统模型，对熨平板的激振器模型进行简化，如图1所示。建立XOY坐标系，M为熨平板的质量，m为质量偏心块，R为转动半径，ω为振动频率，t为时间。2个偏心块同步反向旋转，转角均为ωt。对于同步反向旋转的偏心轴，激振力作用在熨平板上，使其产生竖直方向的往复运动。F0为激振力的幅值，F0=2mRω2。系统的非线性振动微分方程为

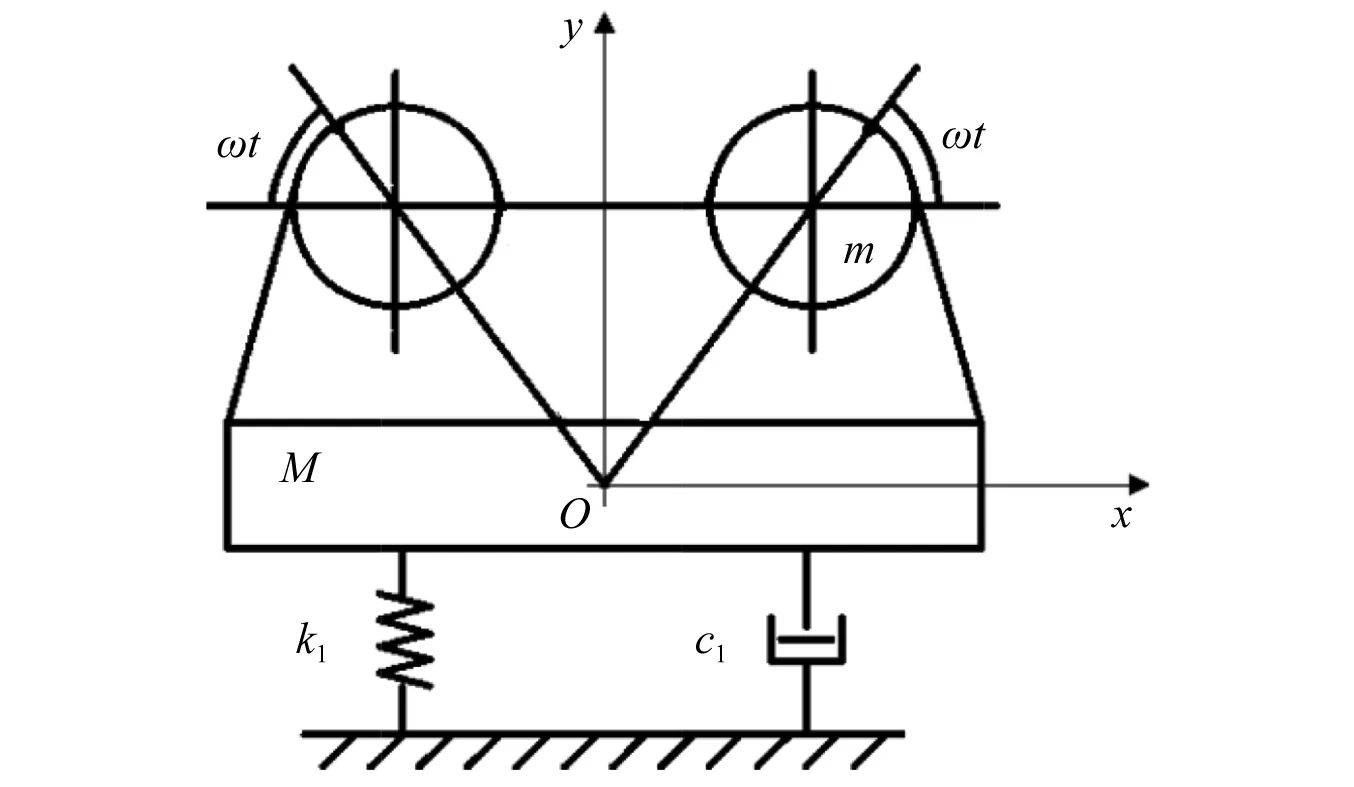
图1 熨平板的激振器模型Fig.1 Vibration exciter model of screed plate

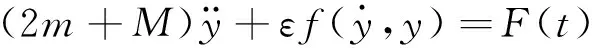
(2)

(3)

其中，

(4)

式中：c1为等效阻尼系数；k1为等效刚度系数。

振动微分方程的稳态响应为

y=Yei(ωt-φ)

(5)

式中，Y为实量振幅，将响应代入微分方程式(3)，可得

[-ω2(2m+M)+k1+iωc1]Ye-iφ=F0

(6)

则稳态响应的幅值为

(7)

(8)

式中：ω0为系统的自然频率；ζ为材料的阻尼比；λ为频率比。

熨平板的激振力通过振动传递路径传递到接受体。在这里是通过弹簧和阻尼的形式传给受体，则摊铺压实过程中，沥青混合料从熨平板获得的摊铺压实力Fc为

(9)

熨平板与沥青混合料之间相互作用的摊铺压实力Fc的幅值为

(10)

在摊铺机熨平板的振动压实过程中，激振力的能量是通过振动熨平板传递到沥青混合料，沥青混合料从熨平板获得的压实力可通过实际摊铺压实力的幅值|Fc|来描述。

1.2 摊铺密实度趋势模型

在摊铺过程中，压实能量通过熨平板传递给沥青混合料。能反映熨平板的振动特性的参数有振动位移、速度、加速度、激振器振幅、激振力和频率等，其中振幅是影响压实效果的重要参数。由共振理论可知，发生共振时，振幅可达到最大值。在工作过程中，激振器的振动频率的大小可以通过调节偏心轴的转速来改变。为了直观的分析熨平板的振动频率与铺层材料密实度的关系，将式(8)中的振动频率放大显示，建立振幅放大因子γ。如式(11)所示。

(11)

根据共振理论，振动频率接近材料的共振频率，激励幅值变高，颗粒内摩擦阻力减小，压实效率变高。根据共振理论和式(11)，可建立密实度趋势模型。如式(12)所示。

(12)

式中:P1为熨平板的振动频率为0时摊铺材料的密实度；A为熨平板压实对沥青混合料密实度的影响系数，它取决于材料类型、级配和层厚等。

2 摊铺过程动态响应分析

通过对图1模型的计算和试验的反求解分析，可得出刚度和阻尼参数值，根据式(3)可求得熨平板所受激振力幅值。压实系统计算参数如表1所示。

表1 压实系统计算参数表Tab.1 Compacting system calculation parameters

通过压实机构动力学模型的建立，可以得到摊铺密实度频率变化曲线，如图2所示。随着频率的变化，摊铺密实度频率特性曲线存在峰值。峰值对应的振动频率出现在频率比λ=1的偏右侧，材料阻尼比值越大，其偏离程度越大。当ω<ω0时，随着振动频率的增加，摊铺密实度呈明显的增长趋势，当ω达到系统自然频率附近时，摊铺密实度达到最大值后，随着ω继续增加，摊铺密实度缓慢减少，逐渐趋向稳定。共振特性对摊铺密实度的影响与材料的阻尼比有密切关系，当阻尼比小于0.5时，对共振特性的影响非常明显，曲线峰值变化明显，当阻尼比的值大于0.5时，对共振特性的影响程度较低，曲线峰值无明显变化。材料的阻尼比值小于0.5时，频率比在0.9～1.5区域的摊铺压实效果较好[24]，阻尼比值大于0.5的材料，振动频率高于系统自然频率时均能够获得较好的摊铺压实效果。

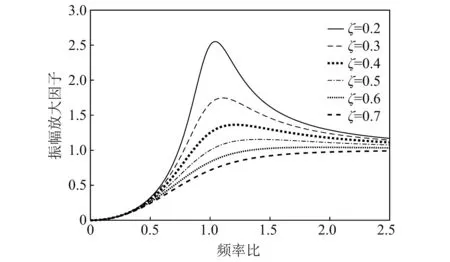
图2 摊铺密实度频率特性曲线Fig.2 Frequency characteristic curves of paving compactness

通过模型分析，可得出摊铺压实力频率特性曲线，选取对共振特性影响明显的阻尼比范围进行分析，如图3所示。随着频率的变化，摊铺压实力频率特性曲线存在峰值，峰值出现在频率比λ=1的偏左侧，材料阻尼比值越大其偏离程度越大；当ω<ω0时，随着ω增加，摊铺压实力呈明显的增长趋势；当ω达到系统自然频率附近时，摊铺压实力达到最大值后，随着ω继续增加，摊铺压实力下降，逐渐趋向稳定；通过计算可知，频率比λ=1.41时，沥青混合料获得的摊铺压实力不受材料阻尼特性影响；当频率比λ>1.41时，材料的阻尼比越大，获得的摊铺压实力越大，此时摊铺压实力不存在明显的增长趋势，受共振特性影响较小，在此范围选取振动频率进行摊铺时，激振力的能量吸收效率较低，无论材料阻尼比为多少，因避免在此范围选取振动参数。

图3 摊铺压实力频率特性曲线Fig.3 Frequency characteristic curves of paving compaction force

结合上述分析，对于阻尼比值小于0.5的材料，理论上选取频率比λ=0.9～1.41作为高密实度摊铺的最佳振动压实区。

通过摊铺密实度趋势模型的建立，对连续级配沥青混合料AC-20进行分析，可以得到对应该材料的摊铺密实度趋势-频率关系曲线，如图4所示。随着频率的变化，沥青混合料AC-20的摊铺密实度存在峰值，值为90.8%，对应的频率比λ=1.2；当对应的频率比λ<1.2时，随着λ增加，摊铺密实度呈明显的增长趋势；当λ>1.2时，随着λ增加，摊铺密实度降低，降低趋势缓慢；振动频率在自然频率附近时，混合料的摊铺密实度值较大，此时的摊铺压实效果较好。

图4 摊铺密实度趋势-频率关系曲线Fig.4 Relation of frequency and density

在摊铺压实过程中，将摊铺密实度达到90%以上时对应的频率比λ的范围作为该沥青混合料高密实度摊铺的工艺参数范围，在此范围内选择振动频率值，可以得到高密实度摊铺的效果。

结合图中显示并提取数据，达到高密实度摊铺的沥青混合料其对应的频率比λ的范围是0.95～1.41，与理论选取的高密实度摊铺最佳振动压实区范围基本一致。

3 摊铺过程振动压实试验

3.1 试验材料与设备

为了验证仿真结果的正确性和有效性，需要进行现场测试。以某工程为例，进行现场试验研究。试验采用DYNAPAC-141全液压履带式摊铺机。熨平板的激振系统为双轴并联式振动系统。工作频率的可调节范围在0～60 Hz。试验选用沥青混凝土AC-20作为试验材料。AC-20属于连续级配沥青混合料，级配数据如表2所示。

表2 AC-20级配数据表Tab.2 Gradation data of AC-20

粗集料采用玄武岩砾石，细集料采用石灰岩碎石，矿粉采用石灰石。沥青采用SBS聚合物改性结合料，基质沥青采用A级90号石油沥青，沥青25 ℃的针入度为60×10-1mm，5 ℃的延度为49 cm，软化点为73 ℃。沥青含量为4.3%。

密实度检测采用CMS-01密实度检测系统，如图5所示。该密实度检测系统是课题组自主研发制成。CMS-01密实度检测系统的主要工作原理是在摊铺机的熨平板上安装密实度传感器，通过密实度传感器对振动的加速度信号进行采集与分析，在相关算法的基础上，计算出能够反映沥青混合料密实度的压实值，经过相关的数理统计分析，得到铺层的密实度值。密实度传感器主要由加速度传感器与速度传感器组成。加速度传感器测得的熨平板加速度信号经放大、滤波后送入控制器进行分析处理。

图5 CMS-01密实度检测系统在现场使用Fig.5 CMS-01 used in density test site

3.2 试验方案

试验过程中，为消除摊铺速度对沥青路面摊铺密实度的影响，设置摊铺机的行驶速度为固定值，摊铺机速度设定为2 m/min，摊铺宽度3.7 m，摊铺厚度60 mm。设置不同的振动频率值对沥青混合料进行摊铺压实，对不同频率下完成摊铺且未使用压路机进行碾压的混合料使用CMS-01密实度检测系统对试验密实度进行检测。试验方案如表3所示。

表3 试验方案Tab.3 Test scheme Hz

3.3 试验结果

采用上述试验设备与试验方案，对连续级配沥青混合料AC-20进行了现场试验，AC-20的密实度-频率曲线如图6所示。由图6可知，沥青混合料的摊铺密实度随着振动频率的增加呈增长趋势，在振动频率f=35 Hz时，摊铺密实度达到最大值，值为91%。AC-20摊铺频率的高效压实区为33～49 Hz，仿真结果与试验结果的变化规律基本一致，模型具有有效性。

图6 AC-20密实度-频率曲线Fig.6 Compactness and frequency curve of AC-20

4 结 论

对沥青路面高密实摊铺建立了一种考虑材料特性与摊铺压实力的熨平板-沥青混合料相互作用振动系统动力学模型，经过分析得出了熨平板的工艺参数对沥青路面摊铺密实度的影响规律，并得出了以下结论：

(1)摊铺压实过程中，熨平板对不同阻尼特性的沥青混合料都存在高密实度摊铺振动参数，在高密实度摊铺的高效压实区选取振动频率可以使材料更易密实，获得最大摊铺密实度。材料的特性会影响系统的自然频率，最佳振动频率值的选择应考虑熨平板-沥青混合料相互作用振动系统的频率特性。

(2)频率比λ=0.9～1.41为高密实度摊铺的最佳振动压实区，将摊铺时熨平板的振动频率匹配在该范围内，可以得到能量吸收效率较高，摊铺压实效果较好的高密实度铺层。

(3)连续级配沥青混合料AC-20的最佳振动频率为35 Hz，最大摊铺密实度值为91%，摊铺频率的高效压实区为33～49 Hz，与仿真分析得出的最佳振动压实区范围基本一致，验证了模型的正确性和有效性；熨平板-沥青混合料相互作用振动系统动力学模型可用于获得高密实摊铺效果，减少后续压路机的碾压遍数，提高施工效率，减少能源消耗，为沥青路面的高效压实提供依据。