铁路不等跨简支梁桥组合减震系统减震机理及影响参数研究

白维刚， 王军文， 邢晨鹏， 彭 涛， 郭 进,4

(1.石家庄铁道大学 校园建设管理处，石家庄 050043；2.石家庄铁道大学 土木工程学院，石家庄 050043；3.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043；4. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043)

我国西部山区地形复杂，地震风险高，为跨越峡谷修建的大跨度铁路桥梁一般由主桥和引桥组成，主桥多为大跨连续梁或连续刚构，引桥为等跨或不等跨简支梁结构。主、引桥(大、小跨简支梁)的梁高不同导致过渡墩处伸缩缝两侧支座垫石的标高不同，在地震作用下不仅邻梁间易发生碰撞，大跨梁与过渡墩间也容易相撞，邻梁间碰撞不仅会导致梁端局部损伤、支座破损，而且可能引起落梁破坏；梁墩间碰撞产生的巨大撞击力会引起桥墩失效、桥梁垮塌等严重震害。而现有的抗震设计往往对这种碰撞重视不够，未采取有效的构造措施来避免[1]。因此，寻求适用于铁路不等跨桥梁有效的减隔震技术势在必行。

目前，研究较多的减隔震装置主要有铅芯橡胶支座[2]、高阻尼橡胶支座[3]、摩擦摆支座[4]、黏滞阻尼器[5]及金属阻尼器等。国内外已经研制出大量弹塑性钢阻尼器，如X形钢板阻尼器[6]、三角形钢板阻尼器[7]及菱形开洞阻尼器[8]等，此类阻尼器耗能性能稳定但初始刚度小；利用面内屈服方式的矩形剪切板阻尼器[9]及抛物线外形阻尼器[10]等容易发生面外屈曲。轴向屈服耗能阻尼器一般采用无黏结支撑形式，其中屈曲约束支撑(buckling restrained brace，BRB)目前应用最为广泛。BRB有效地解决了普通支撑受压屈曲的问题，具备普通支撑和耗能阻尼器的双重功能[11]。在新型减隔震装置研究方面，陈士通等[12]提出的大跨连续梁锁死销减震技术减震效果显著，但其在铁路简支梁上的适用性还有待考究。孟兮等[13]提出用减震榫对铁路桥梁进行减震，但减震榫在实际安装时，传力筒与减震榫榫头的对准存在一定困难，导致减震榫更换工作比较困难。还有一些学者对钢索限位器[14]、SMA限位器[15]、FRP限位器[16]、钢剪切板耗能限位器[17]的减撞及限位效果进行了分析。也有学者对SMA弯曲杆与钢索组合[18]、橡胶缓冲垫与钢索组合[19]等措施的减震效果进行研究。归纳以上研究发现，由于受弹性应变能力、价格、复位能力等限制，单一减震措施效果并不理想，扬长避短，使用两种或两种以上措施来达到减震目的是未来发展的趋势，并且亟待开发适合于铁路桥梁的既有较强耗能能力又能有效限位防落梁的组合减震系统。

针对以上情况，受“功能分离思想”的启发，本文提出一种新型减震设计构思，将BRB-拉索限位器的组合式多级减震系统[20]应用于铁路不等跨简支梁的纵向，利用其良好的耗能减震性能来抵御地震作用，保护主体结构免于破坏。在介绍组合减震系统的构造形式和工作原理的基础上，以两跨铁路不等跨简支梁桥(simply-supported girder bridges，SSGB)为例，分析了组合减震系统的减震机理和减震效果，同时研究了不同参数对其减震效果的影响。

1 组合减震系统研究

1.1 组合减震系统构造形式及工作原理

组合减震系统主要包括BRB、拉索限位器、限位滑动连接组件以及活动铰，BRB两端分别连接限位滑动连接组件和活动铰，活动铰设置在桥墩顶部处；限位滑动连接组件固定于主梁下端，能够将主梁和桥墩离合时的地震力传递给BRB，进而通过BRB变形来消耗地震能量以及拉索限位器的限位功能，有效防止碰撞和落梁，系统具体构造见图1。

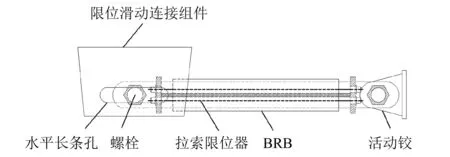
图1 组合减震系统构造Fig.1 Structure of the hybrid shock absorption system

将组合减震系统设置在铁路不等跨桥梁大跨梁与过渡墩间(见图2)，配合活动支座使用，使支座只承受竖向荷载，而组合减震系统只承受纵向水平力。在正常使用情况下，BRB应处于不工作状态，保证桥梁的正常使用；在地震作用下，BRB应达到屈服点，产生塑性变形来消耗地震能量，并且应注意保证BRB不失稳，起到减震和保护主体结构的作用。BRB作为一种耗能结构，吸收梁墩离合时的地震力，通过其弹塑性变形耗散能量。根据限位滑动连接组件的相对位移阈值、BRB良好的滞回性能以及拉索限位器的限位功能，该系统能实现小位移自由变形、中位移耗能、大位移限位防落梁的多级功能。

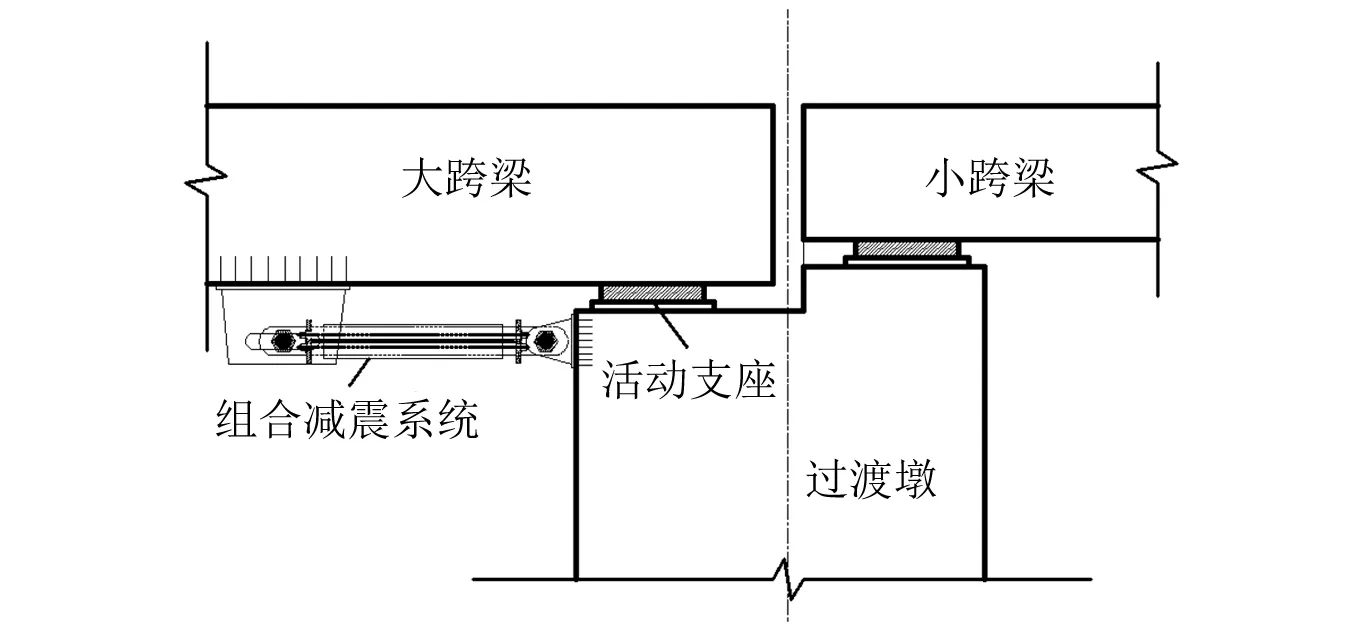
图2 组合减震系统在不等跨桥梁中应用Fig.2 Application of the hybrid shock absorption system on bridges with unequal spans

1.2 组合减震系统单元本构

根据组合减震系统的构造形式及工作原理，其力学模型如图3所示，其中，假定BRB拉、压启动阈值相等，记为gp；kt1和ct1分别为BRB抗压初始刚度和阻尼；ks1和cs1分别为BRB抗拉初始刚度和阻尼；Dg为拉索限位器初始松弛长度，即其工作启动阈值；k1为拉索限位器弹性刚度。

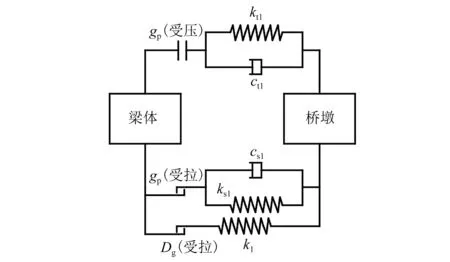
图3 力学模型Fig.3 Dynamical model

组合减震系统的力-位移关系如图4所示，图4中D1和Dg分别表示BRB抗拉屈服位移和最大抗拉容许位移，D2和D3分别表示BRB抗压屈服位移和最大抗压容许位移，Dg也表示拉索限位器的启动阈值，Dm表示组合减震系统最大抗拉容许位移。从图4可以看出，拉索限位器相当于提供了BRB屈服后的二次刚度(或复位刚度)，从而将最大墩梁位移限制在许可范围内。

图4 力-位移关系Fig.4 Force-displacement relation

根据组合减震系统工作原理及力-位移关系，得到该系统单元的本构方程，拉伸情况下单元本构方程为

(1)

压缩情况下单元本构方程为

(2)

式中：ks2，ks3分别为BRB抗拉屈后刚度、BRB抗拉屈后刚度与拉索限位器抗拉刚度的组合值，其中，ks3=ks2+k1；kt2为BRB抗压屈后刚度；vi为墩梁相对速度；D为墩梁相对位移。

组合减震系统中BRB与限位滑动连接组件碰撞过程中的能量损失由阻尼器模拟，其阻尼cp的大小与碰撞过程中的恢复系数e有关[21]

(3)

2 组合减震系统减震机理分析

以某两跨铁路不等跨简支梁桥为例，对组合减震系统的减震机理进行分析，分析时忽略碰撞过程中的能量损失，即取cp=0。

2.1 分析模型

根据铁路工程建设通用参考图：《通桥(2016)2322A-Ⅰ-1》、《通桥(2016)2322A-Ⅱ-1》及《通桥(2017)4301-Ⅳ》，桥梁模型为预应力混凝土简支梁桥，跨径布置为(32+24)m，具体桥梁模型如图5所示。上部结构为单箱单室等高度箱梁，混凝土等级为C50，下部结构采用圆端型2.0 m×6.0 m实体桥墩，C35混凝土；P1～P3桥墩墩高依次为5 m，8 m，12 m，以此来考察相邻桥跨不同动力特性对于组合减震系统的影响，其中，P2为过渡墩。伸缩缝J1间隙大小为3.0 cm，桥梁支座选用KTPZ5500型盆式橡胶支座，每跨设4个支座，S为活动支座，F为固定支座，假定固定支座在地震作用下不剪坏，并在每个活动支座处均布置组合减震系统。

图5 某不等跨桥梁结构示意Fig.5 Layout of a bridge with unequal spans

桥墩P1和梁体D1通过固定支座连接，而梁体D1另一端与桥墩P2通过活动支座连接，两者之间可以相对滑动，因此可以将图5中曲线中的梁体D1、桥墩P1和固定支座的组合体系视为一个自由度；同理，桥墩P2、梁体D2和固定支座的组合体系也作为一个自由度，则两自由度计算模型如图6所示。图中：K1和K2分别为两个桥墩的刚度；M1和M2分别为两个桥墩的质量；Sa为桥梁所处位置的地震加速度；Mg1和Mg2分别为两跨梁体(含桥面系)的质量；kt1，ks1分别为组合减震系统中BRB的受压、受拉刚度；ct1，cs1分别为其相应的阻尼系数；gp为其受压、受拉启动阈值；kl，Dg分别为拉索限位器的弹性刚度、启动阈值；kc1和cc1分别为两自由度体系梁梁间碰撞刚度和阻尼；kc2和cc2分别为两自由度体系梁墩间碰撞刚度和阻尼。

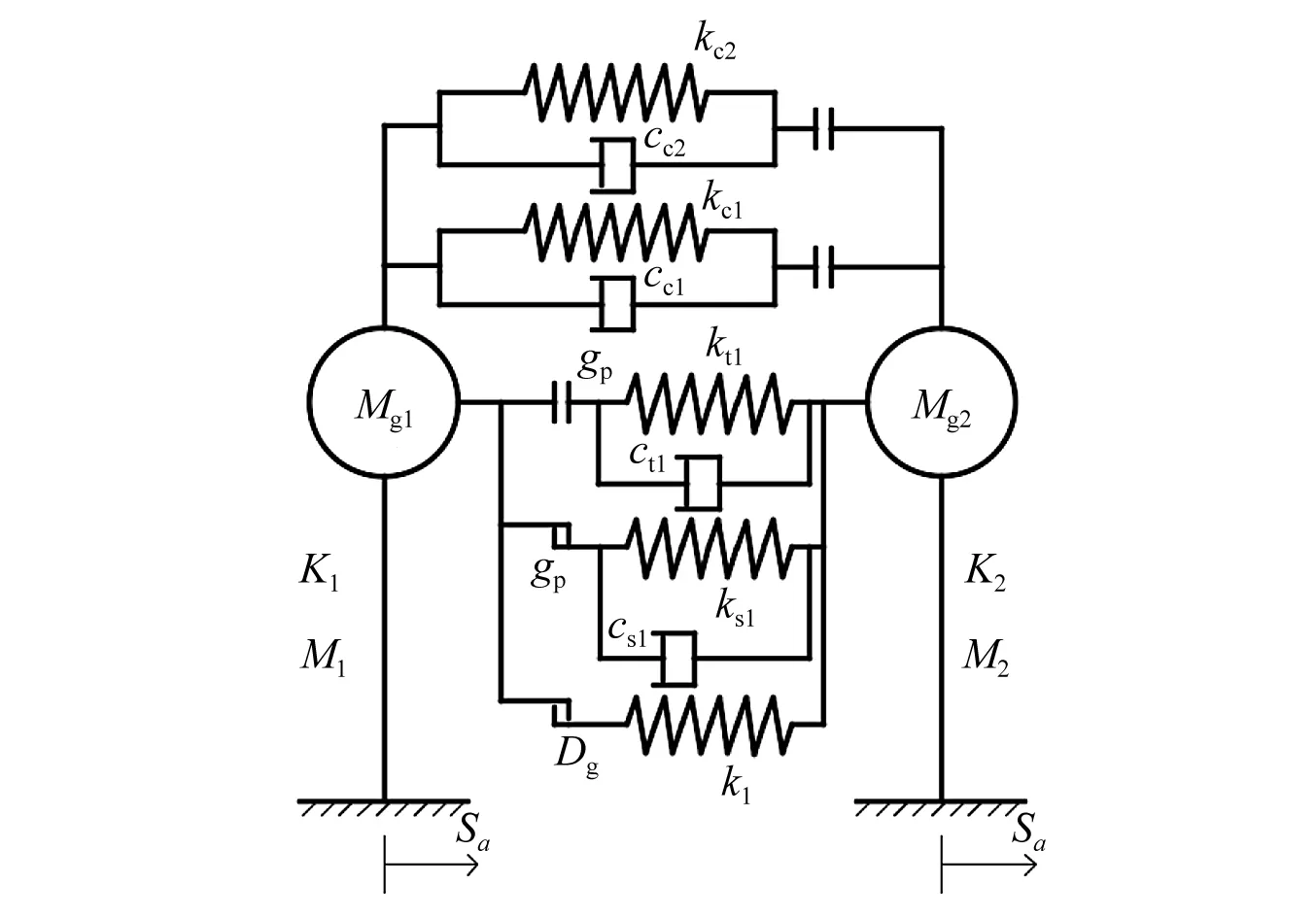
图6 两自由度计算模型Fig.6 Two DOF calculation model

选用OpenSees软件建立计算模型，主梁采用弹性梁柱单元(elastic beam column element)模拟；固定支座采用零长度单元(zero length element)模拟，滑动支座采用平面滑动支座单元(flat slider bearing element)模拟，其滑动向的非线性行为采用双线性滞回材料来模拟；经计算，32 m梁活动支座剪切刚度取5.174×104kN/m，24 m梁支座剪切刚度取3.015×104kN/m，摩擦模型采用库伦摩擦模型，摩擦因数μ取0.03[22]；支座与主梁、桥墩的连接均采用刚臂；桥墩采用基于位移的梁柱单元(disp beam column element)进行模拟，墩底固结，不考虑桩-土作用。碰撞采用双线性碰撞模型进行模拟，利用碰撞材料(impact material)和零长度单元模拟桥梁结构的纵向碰撞，其恢复力模型如图7所示。图中：δy为屈服位移，Kt1，Kt2和Keff分别为碰撞初始刚度、屈后刚度和等效刚度，参考文献[23]，经计算可得邻梁间Kt1取5.596×106kN/m，Kt2取1.928×106kN/m；梁墩间Kt1取2.478×105kN/m，Kt2取8.538×104kN/m。

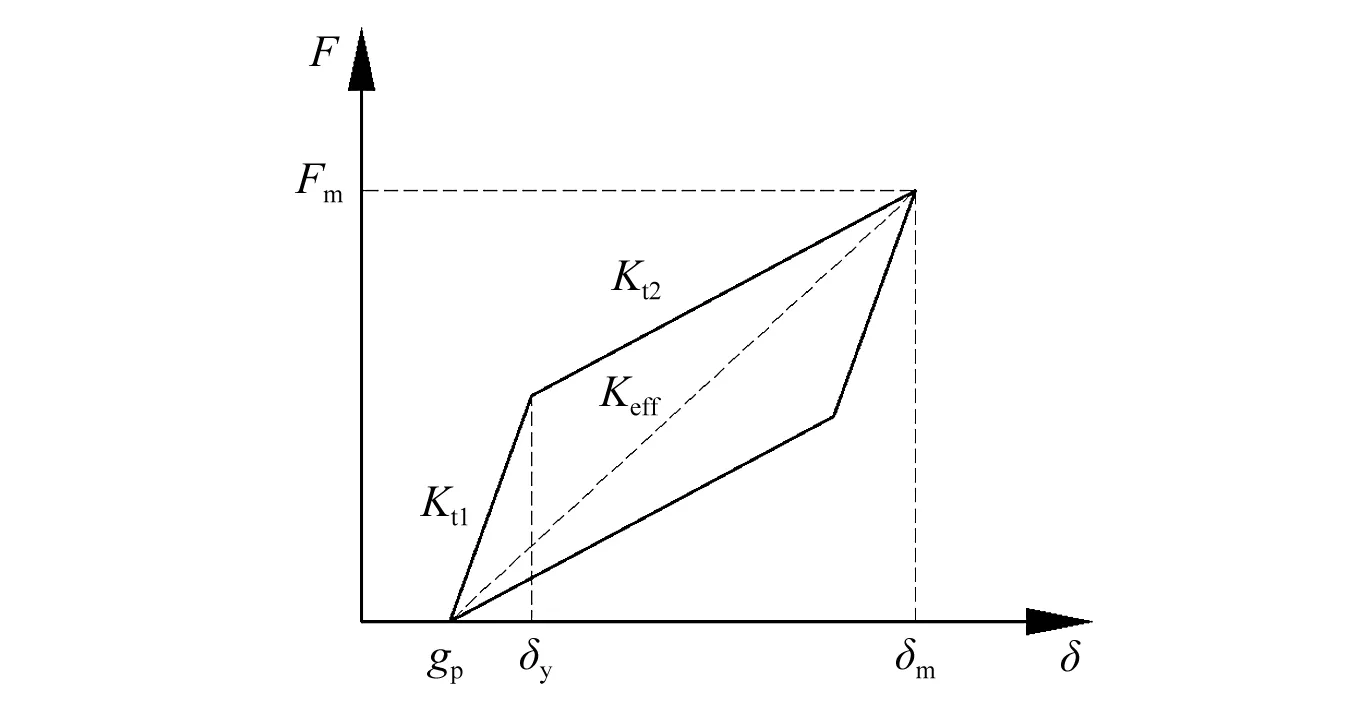
图7 碰撞材料恢复力模型Fig.7 Restoring force model of impact material

考虑到组合减震系统恢复力模型的多重非线性，BRB(含滑动限位连接组件初始间隙)选用零长度单元和多重非线性滞回材料(hysteretic material)进行模拟，拉索限位器选用零长度单元和理想弹塑性间隙材料(ElasticPPGap Material)来模拟，BRB和拉索限位器与主梁和桥墩的连接均采用刚臂。基于正交试验设计对BRB的延性和耗能进行参数敏感性分析，确定出单根BRB全长取1 680 mm，芯材选Q235钢材，长度取900 mm，宽厚比取12.5(内芯板宽为100 mm，厚为8 mm)，其初始刚度为228 kN/mm，屈服位移为1.886 mm。由于BRB屈服位移较小，为满足桥梁在正常运营情况下温度变形、混凝土收缩徐变等需求，滑动限位连接组件初始间隙设置为10 mm，BRB屈服后受压刚度比为0.025，屈服后受拉刚度比为0.023。参照文献[24]，计算出拉索限位器的刚度需求为56 kN/mm，考虑一定的安全储备，确定拉索限位器需4束钢绞线，启动阈值设为30 mm，单束钢绞线长度为1 880 mm(考虑锚固长度)。

2.2 减震机理分析

设工况1、工况2分别为无减震装置、设置组合减震系统，将3条Ⅱ类场地的地震动记录峰值加速度调整至0.38g(见表1)，沿纵桥向输入。为分析减震系统的减震效果，定义减震率λ为

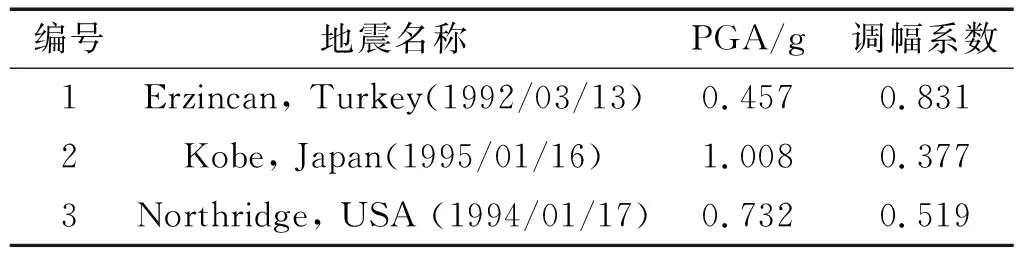
表1 输入地震动列表Tab.1 Input ground motions

(4)

式中，e，es分别为无、有减震装置时结构地震响应峰值。

表2、表3及表4分别为2种工况下桥墩墩底内力、碰撞力及位移分析结果。

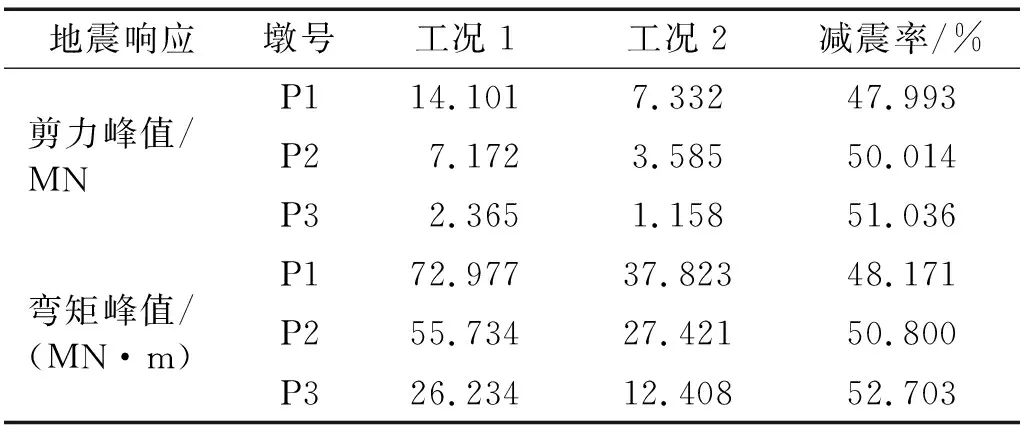
表2 桥墩墩底内力响应及减震效果Tab.2 Response of internal force and damping effect of the bottom of bridge piers

表3 邻梁间、梁墩间碰撞力及减震效果Tab.3 Pounding force and damping effect between adjacent decks or beam and pier

由表2可以看出：采用组合减震系统后墩底内力的减震率均达到47%以上，减震效果非常明显。

由表3可以看出：采用组合减震系统后，3条地震波下邻梁间、梁墩间碰撞力峰值均为0，说明邻梁间、梁墩间均未发生碰撞，减震率为100%。

由表4可见，采用组合减震系统后，梁体纵桥向位移、过渡墩墩顶位移、邻梁相对位移及梁墩相对位移峰值的减震率均在38%以上。为了更加直观呈现组合减震系统对梁体的减震效果，给出了2种工况在3条地震波下24 m主梁纵桥向的位移时程曲线(见图8)和相应的组合减震系统的滞回耗能曲线(见图9)。结果显示：采用组合减震系统后，3条地震波作用下24 m主梁位移均大幅减小，组合减震系统发挥了显著的耗能减震作用，减震效果十分明显。

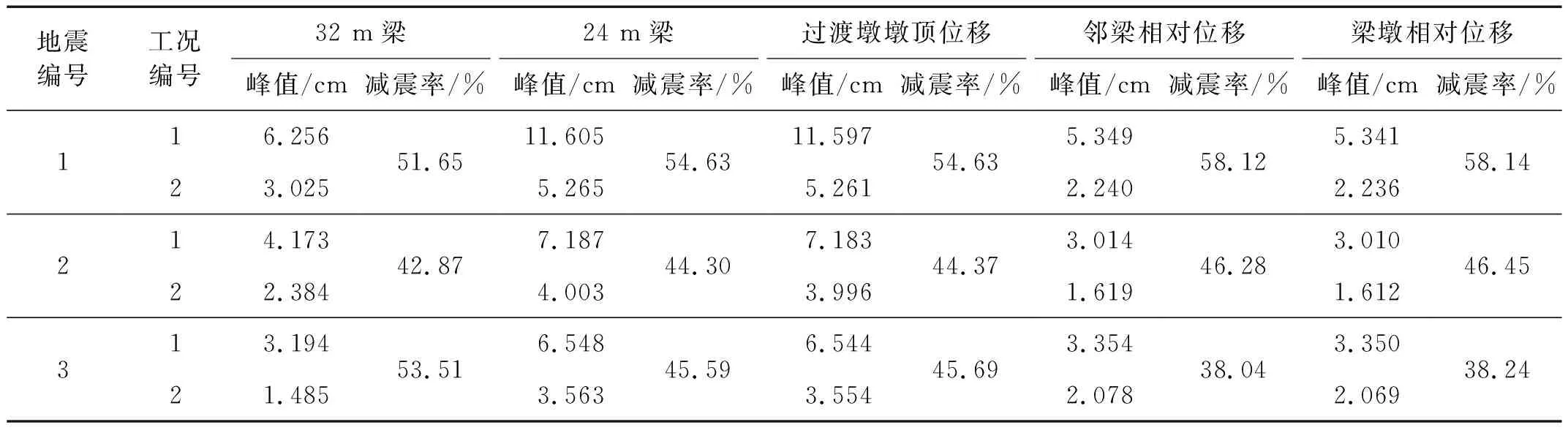
表4 桥梁地震位移响应及减震效果Tab.4 Seismic displacement response and damping effect of bridges

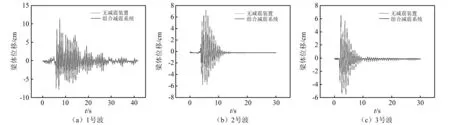
图8 两种工况下24 m主梁位移时程对比Fig.8 Comparison of 24 m beam displacement time-history in two conditions

图9 组合减震系统滞回曲线Fig.9 Hysteretic curves of the hybrid shock absorption system

3 参数影响分析

组合减震系统具有良好的减震效果，但由于系统本身属于复杂的非线性系统，其耗能限位效果受到BRB初始刚度和启动阈值、伸缩缝间隙等参数的影响。

计算模型采用第2章中模型，伸缩缝间隙取4 cm。定义组合减震系统BRB初始刚度K=228 kN/mm，启动阈值δp=1.5 cm，屈后刚度比与前节相同。组合减震系统的影响分三种工况：①无减震装置；②考虑组合减震系统(BRB+拉索限位器)；③仅考虑BRB装置，忽略组合减震系统中拉索限位器的影响。

3.1 BRB初始刚度的影响

图10给出了BBR初始刚度对邻梁相对位移和碰撞效应的影响。

图10 BRB初始刚度对邻梁相对位移和碰撞效应的影响Fig.10 Effect of initial stiffness of BRB on relative displacement and pounding of adjacent decks

由图10(a)可知，在不同BRB初始刚度下，组合减震系统对邻梁相对位移有一定抑制作用，BRB初始刚度越大，邻梁相对位移的减小程度越大。由图10(b)可知，组合减震系统能够有效地减少邻梁碰撞次数和邻梁碰撞力，随着BRB初始刚度的增大，邻梁碰撞次数和碰撞力总体上均呈下降趋势。

3.2 BRB启动阈值的影响

图11为BBR启动阈值对邻梁相对位移和碰撞效应的影响。

图11 BRB启动阈值对邻梁相对位移和碰撞效应的影响Fig.11 Effect of starting threshold of BRB on relative displacement and pounding of adjacent decks

从图11(a)和图11(b)可以看出，当BRB启动阈值在1.5 cm以下时，BRB启动阈值对邻梁靠近位移和碰撞效应的影响不显著，邻梁靠近位移和碰撞效应更多受到桥墩弹性刚度的影响，BRB启动阈值的变化并不是主要影响因素；当启动阈值在1.5～2.5 cm时，BRB能更好地发挥其滞回耗能作用，对邻梁靠近位移和碰撞力的限制效果随启动阈值的增大而增强，邻梁碰撞次数则随之增多；当启动阈值达到2.5 cm逐渐接近伸缩缝间隙，导致BRB滞回耗能效果逐渐降低，BRB对邻梁靠近位移和碰撞效应的抑制效果减弱。组合减震系统中的BRB与拉索限位器对邻梁远离位移均有明显的减小效果，而且拉索限位器的效果要好于BRB，BRB的限位效果随BRB启动阈值增大而减弱，拉索限位器的限位效果对BRB启动阈值变化不敏感，说明在组合减震系统设计中应加大对拉索限位器的重视程度。

3.3 伸缩缝间隙的影响

图12～图14分别给出伸缩缝间隙对邻梁相对位移、碰撞效应及过渡墩地震响应的影响。

图12 伸缩缝间隙对邻梁相对位移的影响Fig.12 Effect of expansion joint gap on relative displacement of adjacent decks

图13 伸缩缝间隙对邻梁碰撞效应的影响Fig.13 Effect of expansion joint gap on pounding of adjacent decks

图14 伸缩缝间隙对过渡墩地震响应的影响Fig.14 Effect of expansion joint gap on seismic response of transition pier

由图12可以看出，当伸缩缝达到5 cm后，BRB装置对邻梁靠近位移减小效果明显；设置组合减震系统对邻梁远离位移减小效果较好；而且设置组合减震系统桥梁的邻梁远离位移值要小于BBR减震装置，说明组合减震系统中拉索限位器对邻梁远离位移起到积极的限制作用，可防止桥梁在强震下出现落梁危害，邻梁远离位移对伸缩缝间隙大小不敏感。

由图13(a)可以看出，邻梁碰撞次数随伸缩缝间隙增大而减少，且BRB减震装置可有效减少邻梁碰撞次数。由图13(b)可知，随着伸缩缝间隙的增大，不设减震装置时邻梁碰撞力呈先增大后减小的变化趋势；设置BRB减震装置或组合减震系统能有效降低邻梁碰撞力，且碰撞力随伸缩缝间隙增大而减小，当伸缩缝在5 cm以下时，组合减震系统比单纯BRB装置对邻梁碰撞力的减撞效果更好。

从图14可以看出，随伸缩缝间隙的增大，安装减震装置前过渡墩的墩顶位移、墩底剪力及弯矩逐渐增大，其中位移增加不如内力增加得快；设置减震装置后三种响应的增速减缓，当伸缩缝达到5 cm后趋于稳定。过渡墩墩顶位移、墩底剪力(弯矩)设置组合减震系统时要比仅设置BRB装置时分别略小、略大，说明拉索限位器可以减小过渡墩墩顶位移响应，增大墩底内力，所以在设计中应充分考虑，以免桥墩发生塑性破坏。

4 结 论

(1) 在铁路不等跨简支梁桥设置BRB-拉索组合减震系统，可显著减小过渡墩墩底地震响应，保护桥墩，减震率达到47%以上；降低邻梁间、梁墩间发生碰撞的风险；减小简支梁纵向地震位移响应，减震率在38%以上，说明该系统具有较好的减震效果。

(2) BRB初始刚度和启动阈值均对简支梁邻梁相对位移产生一定影响，且组合减震系统对邻梁远离位移的抑制效果比较明显；BRB初始刚度越大，邻梁相对位移的减小程度越大，BRB启动阈值的改变对邻梁靠近位移和碰撞效应的影响较大，设计时应根据BRB本身滞回耗能强弱和伸缩缝间隙大小进行合理选择，并加大对拉索限位器的重视程度。

(3) 当伸缩缝间隙达到5 cm以上，组合减震系统对邻梁相对位移、碰撞力及碰撞次数的减震率较大；拉索限位器可以减小过渡墩墩顶位移响应，增大墩底内力，所以在设计中应充分考虑，以免桥墩发生破坏。

(4) BRB的初始刚度、屈后刚度、启动阈值可根据桥梁结构参数初步确定，拉索限位器的刚度和启动阈值则需满足BRB恢复力需求和安全性要求；再加以地震分析对BRB初始刚度和启动阈值、拉索限位器刚度和启动阈值进行调整，其中BRB和拉索限位器的启动阈值是需要关注的重点，也是组合减震系统功能得以发挥的关键；以上参数如何确定课题组正在进行后续研究。