基于幂律分布的浮冰生成方法及船-冰碰撞分析

石原赫， 刘 昆， 俞同强， 王加夏

(1. 上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240;2. 江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

随着对北极航道的开放及全球气候变暖，极地航行船舶船长由过去的约100 m逐渐增大到如今普遍的大于100 m，航行速度也越来越快[1]，与此同时，冰川的加速融化导致北极可通航区域及航行时间快速增长，冰盖区与开阔水域中间的边缘冰区浮冰数量也逐渐增加。而边缘冰区的浮冰分布一直发生着变化，从冰盖区往开阔水域扩散。这使极地航行船舶通过夏季边缘冰区时，浮冰与船舶的碰撞次数逐渐上升，对于长时间在北极航行的船舶必然会造成一定的安全隐患。因此对夏季边缘冰区的浮冰分布及船舶与浮冰碰撞进行研究显得尤为重要。

船舶与浮冰的碰撞需观察浮冰的分布变化，将浮冰分布变化导入有限元中进行碰撞分析。浮冰分布的观测数据主要依靠卫星、航拍及船舶航行提供。基于不同的数据来源，学者们对不同地区、不同范围内的浮冰分布进行了研究。Matsushita[2]根据卫星图像技术识别出浮冰尺寸及数量，以浮冰数量密度分析得出浮冰大小分布符合幂律分布规律。Lu等[3]通过航拍和船载设备得到的数据对直径小于100 m的浮冰分布进行了研究，发现浮冰尺寸同样符合幂律分布规律，幂指数在1.4～2.2。在碰撞模拟分析中，通常只考虑了浮冰的单一形状特征。Wang等和Guo等[4]分别就同一尺寸和6种不同尺寸的方形冰沿航行方向矩阵排列，对船-冰碰撞中阻力进行了分析。Yulmetov等[5]以Lu等的累积分布函数对一定直径范围内的凸形浮冰进行了研究，生成的浮冰比方形冰更具随机性。然而浮冰大小和形状是不同的独立特征，只有其一不能准确的描述浮冰分布情况，因此两者都要充分考虑。同时由于分布数据受限于地点、范围等，目前得到的浮冰分布数据还很有限，而浮冰分布多是获取的夏季数据，因此本文所研究的浮冰生成方法同样基于夏季边缘冰区的浮冰分布。

典型船-冰碰撞问题中，流体动力载荷不被作为主要考虑因素，但是当船舶撞击浮冰时会有明显的水动力载荷产生，而水动力载荷直接决定着船-冰碰撞模拟结果的准确性，在船-冰碰撞分析中不可忽略[6]。郭春雨等[7]使用LS-DYNA软件通过流固耦合(fluid-structure interaction，FSI)法模拟船舶与碎冰碰撞，分析不同密集度和速度下的碰撞力，但在数值模拟中对船舶垂向位移进行了约束。翟帅帅等[8]则基于Derradji-Aouat海冰本构模型，对连续式和冲撞式破冰采用流固耦合法进行了数值模拟，研究了破冰船局部强度和总纵强度。其船舶简化为刚体，对海冰所受浮力用一维非线性弹簧单元来进行模拟。Zhu等[9]对简化的矩形刚性板与不同尺寸的浮冰块进行了碰撞分析，通过损伤能量折减比得到浮冰的形状和宽度对碰撞结果有着明显的影响。Kim等[10]随机生成尺寸、形状特征的四边形模型冰进行船冰相互作用模拟分析，并进行了同等条件的模型试验。但结果的准确性受到条件假设和模型简化的限制，需与全尺度模拟的数据进行对比研究。

为了更准确的得到碰撞结果，船-冰碰撞模拟中的浮冰场应该尽量符合实际情况。由于碰撞试验代价昂贵、不可重复，对于船-冰碰撞模拟的大多数研究都是基于模型船和模型冰试验的基础上，针对全尺度的船-冰碰撞模拟较少。本文主要通过ANSYS/LS-DYNA软件生成夏季尺寸、形状随机的凸多边形浮冰，在此基础上，基于流固耦合法对全尺度极地航行船舶与浮冰场进行碰撞模拟损伤研究。

1 极地浮冰概率分布模型及生成方法

1.1 浮冰概率分布模型

由于浮冰分布的多变性，在研究船舶与浮冰碰撞前应该先给定直径范围，生成合理的浮冰场。将浮冰周围所有方向上的卡尺尺寸的平均值作为浮冰的平均直径(mean caliper diameter，MCD)。由Stern等[11-12]整理的海冰卫星数据和航拍数据可知，自然界中浮冰的直径分布均近似的符合幂律分布。其幂律分布函数为

(1)

式中：N为数量；α和β为常数。

由于对非常小尺度的海冰无法通过航拍和卫星识别出来，而达到一定大尺度的海冰又因为走航观测和航空拍摄方法的区域限制使其无法拍摄完整。故Yulmetov等提出使用累计分布函数来研究浮冰分布情况，即

(2)

式中：Dmin为浮冰的最小直径；α和β为常数。

(3)

通过控制缩放因子a可以提供式(3)中的浮冰直径分布，即

(4)

由随机变量商的性质，可知a的概率密度函数为

(5)

为了更简单的计算α值，将缩放因子a设置为均匀分布变量x的函数，这样只需生成一个均匀变量就可以得到缩放因子a值

(6)

式中，x为在[0,1]内的均匀分布随机数。

通过均匀变量x得到缩放因子a后，就可以得到实际的浮冰直径大小，然后通过给定浮冰场范围及浮冰密集度得到最终的浮冰分布。

1.2 浮冰生成方法

1.2.1 浮冰形状特征参数

在图像识别中海冰的形状特征主要通过面积、周长、圆度、凸度及体态比来表征[13]。其中面积(A)被普遍作为描述海冰二维尺寸特征的依据，包括众多的航拍图片和卫星图像都是以海冰面积对不同大小的海冰进行分类；周长(P)是单块海冰边缘的长度。主要作为海冰图像识别中的形状特征参数，在同等面积和热力条件下，多个小尺寸海冰比大尺寸海冰周长更长；圆度(R)是海冰周长与同等面积的圆周长的比值，主要反映了海冰形状的变化。其值越大，形状越复杂，主要体现为大尺寸浮冰；其值越小，形状越接近圆形，主要体现为小尺寸浮冰；凸度(C)为海冰周长与平均直径的比值，主要体现海冰二维形状的凹凸性。其值越大，海冰形状凹陷程度越大；体态比(G)是根据矩法定义海冰的短轴长与长轴长的比值，体态比描述了海冰二维形状的狭长程度，其值越小，海冰越显狭长；其值增大，海冰狭长程度收敛。

1.2.2 浮冰形状简化

关于圆度，考虑到实际生成的浮冰尺寸在小尺寸范围内，且根据圆度的变化规律，越小的浮冰其值越接近1，形状越近似圆。随着尺寸变大，其圆度值不断增大，浮冰形状也越发复杂化。所以在后续的浮冰生成过程尽可能的让二维多边形接近于圆，以此满足小尺寸浮冰圆度的要求。

关于凸度，由于现实中凹多边形的浮冰较少，同时缺乏关于凹多边形浮冰参数影响冰荷载的信息数据。因此不考虑凹多边形的情况，假设浮冰多边形均为凸多边形。

关于体态比，体态比标志着多边形的狭长程度。现实中浮冰是从冰山或冰盖上分离而来的，然后在向外扩散的过程中再次分离出更小的浮冰。如果分离过程中产生狭长的浮冰，受热力学、碰撞、波浪等影响，其无法维持长时间形状不变。一定会再次破碎，慢慢形成更多的圆形冰。因此，通过限制多边形边数来遏制过于狭长的多边形产生，但并不完全消除长形浮冰。本文选取多边形为五边形至九边形内随机生成。

1.2.3 浮冰生成

基于上述概率分布理论以及浮冰形状的简化要求编写浮冰生成子程序。为了高效的生成多边形，采用先生成二维图形，再统一生成三维立体的方法。图1(a)为浮冰生成流程图，图1(b)为随机生成五边形至九边形浮冰元素的图解。在生成二维图形时采用在冰场中生成随机圆，在其圆周上创建随机点并将这些点首尾相连生成二维多边形。然后根据浮冰直径的幂律分布概率函数确定最终多边形的大小，这里假设生成的浮冰不会由于波浪及自身弯曲等发生额外的断裂。

图1 浮冰生成图解及流程图Fig.1 The diagram and flow chart of floating ice generation

首先确定冰场的范围，给定浮冰直径范围、浮冰密集度和幂律分布缩放系数。在冰场内生成二维随机圆，随机圆是按从大圆到小圆过渡的顺序生成，按照幂律缩放系数对圆进行缩放，其次在圆周上随机生成点连接成多边形，如果生成的多边形与现有的多边形重叠，则删除此多边形，重新搜索位置生成多边形，直到不再发生重叠。在生成多边形的同时计算多边形的面积总和，当达到预先设定的密集度时，生成结束。在二维多边形生成结束时，将所有的多边形沿垂直方向的拉伸，生成三维实体。最后在三维实体上划分单元网格，用于后续的仿真分析中。

一方面，教师应当正确认识自身角色定位，充分发挥其引导作用和辅助作用，在二胡演奏教学和训练的过程中制订科学合理的训练意志目标，层层递进；另一方面，教师应当引导学生根据训练效果的反馈信息正确分辨技巧的正确有效与否，明确自己的优势及应当改进完善的缺陷，有针对性地进行训练，从而攻克一个个技术难点。

1.3 典型冰场的确定

在确定碰撞场景前需先给定典型的浮冰场，这里浮冰的分布由冰场大小、浮冰直径范围、参数β、厚度、密集度限制影响。为了有效地忽略边缘浮冰对于碰撞结果的影响且考虑到船舶尺寸的大小，冰场范围选取为100 m×200 m的矩形航道。

本文以Wang等[14]测量的浮冰直径数据为依据，该时期海域内的浮冰最小直径为5 m，而边缘冰区外围的浮冰最大直径约为20 m[15]。因此，选取浮冰直径范围为5～20 m。

由式(3)可知，β是影响浮冰概率密度分布的一个重要参数，其值大小的变化伴随着不同直径区间内浮冰数量的变化。在浮冰直径范围确定后，随着β值的增大，其较小直径区间的浮冰数量明显增加，同时为了保证浮冰场的密集度不变，其较大直径区间的浮冰数量减小，由于北极夏季浮冰数量较多，直径偏小，β值通常在2左右，故本文中对于β的取值均为2。

北极夏季期间多数为一年冰，一年冰的厚度为0.3～2 m。中国第五次北极考察所统计的海冰厚度分布在0.7～1.7 m内，受海冰密集度不同发生变化。随着地区和冰情的不同浮冰的密集度和厚度也在发生着变化。其中，弗兰格尔岛、东西伯利亚海冰情较严重，海冰密集度在50%～90%内，冰厚在1～1.7 m；楚科奇海冰情相对较轻，海冰密集度在20%～50%内，冰厚在0.7～1.2 m。因此选取冰厚为1 m作为典型冰场浮冰的统一厚度[16]。

根据以上的参数开展浮冰分布数值模拟，如图2所示。浮冰场为100 m×200 m，最小浮冰直径为5 m，最大浮冰直径为20 m，密集度为40%，50%，60%，β取值2。从图2中可以看出：浮冰整体均匀分布在冰场中。由于浮冰的等效直径符合幂律分布；大尺寸浮冰数量明显少于小尺寸浮冰。随着密集度的增加，不同直径区间的浮冰数量也在增加，以此达到密集度的要求。各直径范围内浮冰的形状均为凸多边形，小直径范围内的浮冰形状更容易接近于圆形，受多边形边数影响棱角较圆润，少数体现出矩长形特征，但未见过于狭长类浮冰出现；而大直径范围内的浮冰形状也接近于圆形，但棱角更明显、形状多变，无明显矩长形浮冰出现，这主要是圆度影响所致。

图2 不同密集度下的浮冰分布模型Fig.2 The model of floating ice distribution under different concentrations

2 船舶与浮冰碰撞数值分析

2.1 碰撞场景

本文选取一艘船长为114 m的极地运输船舶作为研究对象，开展流-固耦合下典型冰撞载荷作用结构响应分析，极地运输船舶的主要船参数，如表1所示。由于船舶-浮冰碰撞具有较强的动态非线性、碰撞局部性等特点，而且浮冰撞击区域主要集中在艏柱水线面附近，故对不在碰撞范围内的船体结构做刚体化处理。本文以40号肋位为界限将船舶模型分为艏部弹性碰撞区和艉部刚性非碰撞区，如图3所示。艏部碰撞区结构完整且能够完全包含浮冰碰撞范围，非碰撞区由于没有浮冰撞击，采用同等质量的刚体外壳替换原结构。为了更好的保证船-冰碰撞结果的准确性，需要对模型网格尺寸进行严格控制，以此达到保证计算精度的同时提高计算效率。本文根据张健等[17]的研究，控制船体结构网格尺寸在0.25～0.28 m；流场平面尺寸为340 m×100 m，水域和空气域高度均为10 m，网格尺寸为1 m×1 m×1 m[18]。在此基础上，选取密集度为60%、冰厚为1 m、航速为5 m/s为典型工况，分别对不同密集度下的船-冰碰撞进行模拟。完整的船舶-浮冰碰撞模型，如图4所示。浮冰边界建立固定刚性墙，提供类似实际远处冰排或浮冰的阻力作用，以此达到约束浮冰漂移的目的。

表1 极地航行船舶主要参数Tab.1 Main parameters of polar ships

图3 船艏结构图Fig.3 Diagram of bow structure

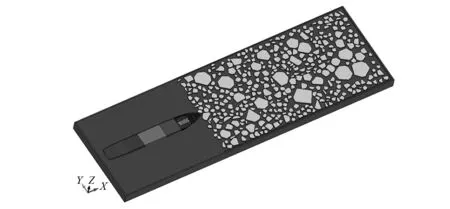
图4 密集度60%全局模型图(隐去空气)Fig.4 Global model with 60% concentration (hidden air)

2.2 材料模型

2.2.1 流体材料模型

LS-DYNA中常采用本构模型和状态方程来描述流体材料(空气、水)模型，分别选取空白材料(NULL Material)和线性多项式状态方程(EOS-LINEAR-POLYNOMIAL)来模拟空气和水。材料主要参数是密度、黏度系数、常数C0～C6、单位体积初始内能、初始相对体积比，具体的数值如表2所示。

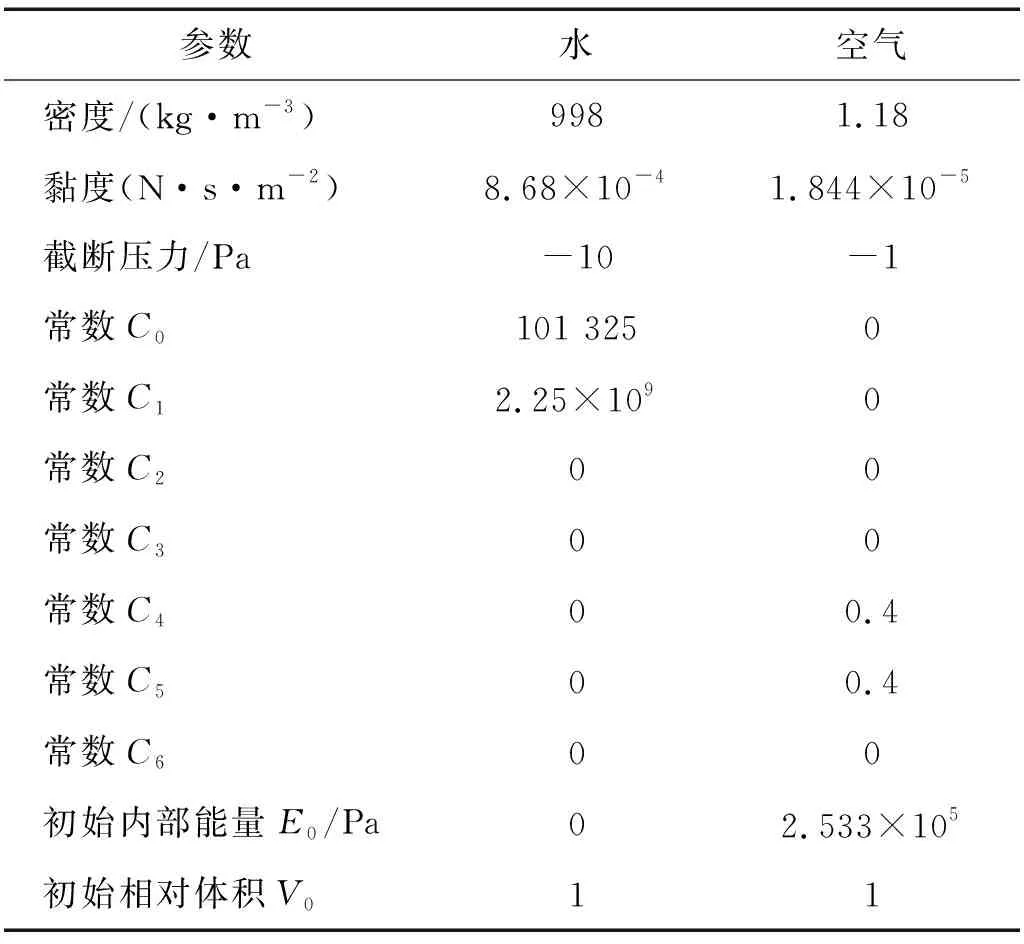
表2 流体材料参数Tab.2 Parameters of fluid material

2.2.2 钢材材料模型

在极地运输船舶航行过程中与浮冰的多次碰撞会对船体结构产生累计损伤的影响，因此合理的选择船体结构材料模型是极地浮冰碰撞模拟分析中的重要内容。北极常年处于低温状态中，一年中冬季温度最低，历年来平均温度约为-40 ℃，最低温度达到-68 ℃左右。温度最高的夏季平均温度也在-10 ℃左右。因此对于极地航行船舶广泛使用的普通钢以及高强钢在低温下材料的力学性能将发生改变，力学性能的改变会影响到船舶与浮冰碰撞下结构的动态响应。本文采用低温高强钢材料来模拟船舶与浮冰的碰撞分析，在LS-DYNA中使用24号弹塑性材料输入，材料参数[19]如表3所示。

表3 钢材料参数Tab.3 Parameters of steel material

2.2.3 浮冰材料模型

海冰材料模型是影响船-冰碰撞结果重要因素之一。由于海冰复杂的材料特性，目前模拟船-冰碰撞过程中海冰的所有行为还是很困难的。因此，选取相对合理的海冰材料模型是进行船-冰碰撞的前提和基础。由于海冰材料在低应变率下为韧性失效，在高应变率下为脆性失效且海冰的应力-应变曲线近似于直线[20]。因此，本文针对高应变率下的船-冰碰撞问题，选取LS-DYNA软件中的第13号弹性材料(*MAT_ISOTROPIC_ELASTIC_FAILURE)对浮冰进行模拟。该材料是带有塑性应变失效准则的各向同性弹性断裂失效模型，当有效塑性应变达到失效应变或当压力达到失效截断压力时，单元失去承载应力的能力。材料参数[21]如表4所示。

表4 浮冰材料参数Tab.4 Parameters of floating ice material

2.3 计算结果与分析

选取典型工况为例，船舶在浮冰场中航行20 s的运动结果,如图5所示。典型工况下随着船舶进入冰场，浮冰发生明显的翻转、堆积、破碎等现象。其中翻转主要发生在小尺寸浮冰上，而大尺寸浮冰多是发生破碎，堆积则以船艏附近较严重，在远离船艏的浮冰之间，堆积现象明显减弱。随着密集度的变化，高密集度下由于浮冰间距减小，撞击后浮冰更易出现典型运动状态；低密集度下由于浮冰平均间距较大，撞击后浮冰主要以破碎为主。

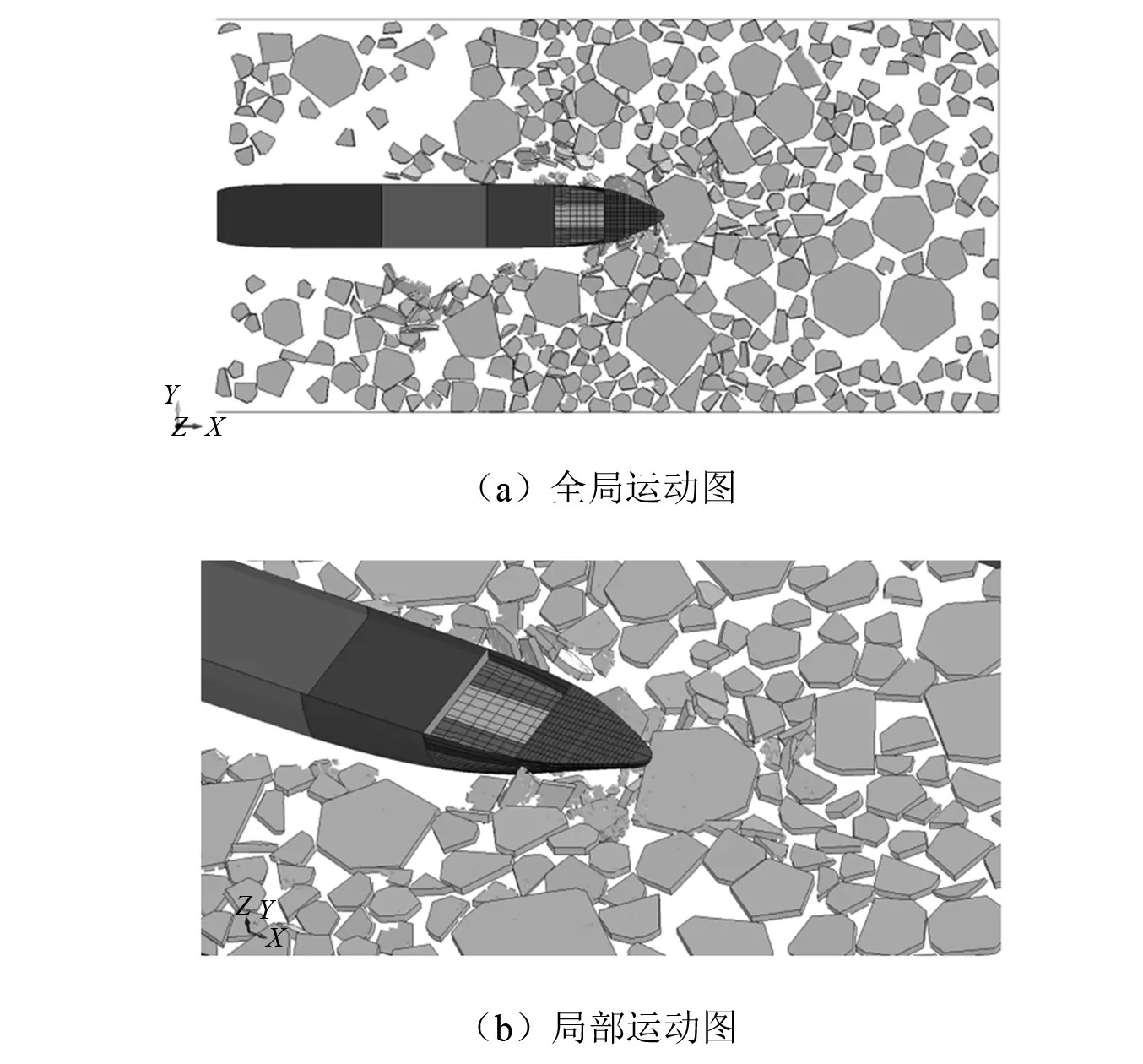
图5 浮冰运动图Fig.5 Diagram of floating ice motion

典型工况下船艏的主要构件损伤变形图,如图6所示。从图6中可以看出各构件的损伤变形程度小，结构未进入塑性状态，没有撕裂、屈曲等破坏形式出现。变形区域主要集中在船艏艏柱的水面附近。随着密集度变化，船艏结构均未出现破坏，浮冰撞击区域由于堆积影响有明显的增加。船艏结构受低温高强钢材料的影响，各构件表现出较好的抗撞性。

图6 主要构件损伤变形Fig.6 Damage and deformation of main members

典型工况及不同密集度下船舶与浮冰的全局碰撞力历程区线，如图7所示。从图7(a)中可以看出，碰撞力曲线具有明显的动态非线性特征且呈现多个碰撞区，主要分为碰撞阶段和非碰撞阶段。当船舶航行距离在a段内时，随着船舶航行导致波浪推动浮冰反向运动，使碰撞不明显；当航行距离在b段时，运动的浮冰受到后方浮冰的阻碍作用，使船舶与浮冰发生持续性碰撞，由碰撞力曲线可以看出浮冰发生多次破碎失效；当航行距离在c段时，由于前面的发生碰撞的浮冰发生破碎并再次被反向推动，碰撞力出现空白期；当航行距离在d段时，浮冰再次受后方浮冰的阻碍与船舶发生持续碰撞，浮冰不断发生碰撞-失效-碰撞-失效循环；后面e段、g段再次出现空白期，但持续距离较前面大大减小；f段为持续碰撞区，可以看出f段和d段两次碰撞区之间的距离缩短；h段再次出现持续碰撞的趋势。整体随着船舶深入冰场，浮冰受波浪及撞击的影响区域性的不断后移，碰撞空白期的距离随着船舶航行距离的增加不断缩短。主要是由于随着船舶航行浮冰不断的移动，导致了航行后期相当于提高了海冰密集度，使碰撞较前期连续。从图7(b)可以看出，在低密集度下，由于浮冰间距较大，初始的碰撞多为短暂性的且持续碰撞发生时间较晚。随着密集度的增加，持续碰撞发生的时间逐渐提前，浮冰碰撞次数增加。而由于浮冰尺寸及分布的原因，碰撞力涨幅不是很大。因此，在中低密集度下，浮冰密集度增加对碰撞次数的影响较大，对碰撞力幅值的影响较小，这也给船舶带来了持续的小能量碰撞损伤。

图7 碰撞力曲线Fig.7 Curve of collision force

浮冰的动能变化曲线，如图8所示。从图8中可以看出，不同密集度下浮冰动能均随着时间的增加而升高。但是由于密集度的增加直接导致浮冰间距缩短，可运动空间减小，不同密集度下浮冰动能变化有所不同。低密集度下浮冰主要受航行波的影响运动，动能保持较平缓增长。在船艏局部密集度增加后，浮冰在撞击作用下动能有明显的上升。随着密集度的增加，浮冰间距减小，其主要受到撞击作用运动，故动能上升较迅速。在船艏局部密集度增加后，高密集度下浮冰的动能更易趋于稳定。

图8 浮冰能量-时间曲线Fig.8 Energy-time curve of floating ice

船舶各构件的能量吸收曲线，如图9所示。从图9(a)中可以看，由于碰撞前期船舶未完全进入冰场，浮冰受航行波的影响反向移动，造成碰撞频率较低，船舶吸能趋于平缓。碰撞后期船舶基本完全进入冰场，浮冰受船舶及固定边界的影响被相互挤压在一起，使碰撞频率相对较高，船舶结构吸能开始呈上升趋势。构件的吸能情况主要以外板、横舱壁、舷侧骨架为主，其次是彼此相差不多的甲板和纵向构件，横向构件吸能最少。吸能值都不是很大，较船舶撞击冰排及正常船舶碰撞能量吸收小了很多。主要是因为浮冰在自由的漂移，撞击不连续，而后续随着浮冰的堆积，相当于海冰的密集度增加，此时整体吸能有明显的提升，说明海冰的密集度对碰撞力及吸能有着重要影响。

从图9(b)可以看出，随着密集度的变化，船艏结构总吸能均呈上升趋势。航行前期结构总吸能主要受浮冰密集度及分布变化影响，其结构起始总吸能有所不同且上升趋势较平缓；随着船艏局部密集度的增加，船舶撞击频率上升，结构总吸能上升较快速，但还是处于小能量碰撞范围内。

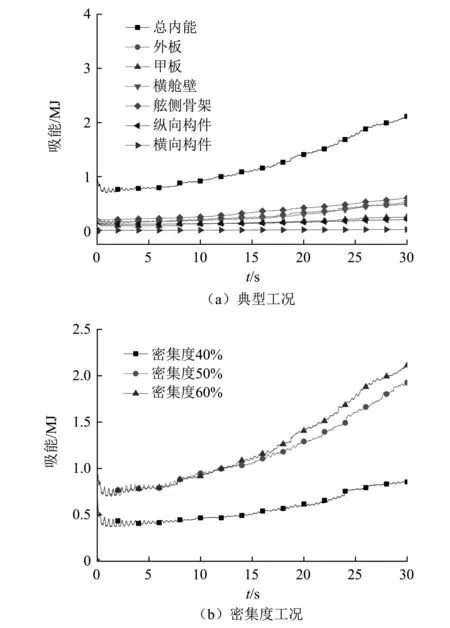
图9 船舶构件能量-时间曲线Fig.9 Energy-time curve of ship members

3 结 论

本文在幂律分布理论及海冰形状识别特征的基础上，在ANSYS软件中编制浮冰生成程序，实现了对一定直径范围内圆度接近1、体态比相对正常、整体为凸多边形的浮冰随机生成；采用流-固耦合法开展了极地运输船舶与浮冰连续碰撞的数值模拟计算，通过计算结果得出如下结论：

(1)在同一密集度下，随着船舶航行距离增加，浮冰翻转、堆积及破碎典型现象在船艏撞击区域明显。其中翻转主要发生在小尺寸浮冰上，大尺寸浮冰则主要发生破碎现象。远离船艏的浮冰主要受航行波的推动发生轻微的破碎失效。

(2)随着密集度的变化，浮冰的主要典型运动状态也在发生着变化。低密集度下浮冰的典型运动状态以破碎为主；高密集度下浮冰的翻转、堆积现象逐渐严重。

(3)随着密集度的增加，船艏结构变形范围增大。主要集中在艏柱水线附近，结构变形较小。短期航行期间不会造成船体结构的破坏，但是长期航行下去所带来的疲劳损伤不可忽视。

(4)船舶撞击浮冰的碰撞力及船体结构吸能值与正常的船舶碰撞、船舶-冰排碰撞相比均较小，船艏构件损伤变形不明显，浮冰连续碰撞是处于小能量碰撞范围。船舶在浮冰场中航行时，浮冰连续碰撞导致的疲劳损伤及浮冰堆积导致的碰撞频率上升是船舶在浮冰场航行的较危险情况。当长时间处于这种情况时，船体结构的疲劳损伤情况是不确定的，这也是一个值得研究的问题。