分布式存储系统中新型可修复喷泉码构造

周安安, 易本顺, 刘羽升, 罗来干

(武汉大学电子信息学院, 湖北 武汉 430072)

0 引 言

随着现代信息技术的快速发展,数据生成速度迅猛提高,根据IDC发布的最新版白皮书《Data Age 2025》显示,预测2025年全球数据量将从2019年的45 ZB增长到175 ZB,其中将近30%将需要实时处理[1]。在数据存储领域,海量数据的增长使得分布式存储系统受到了更多关注。在大规模分布式存储系统当中,由于其组件通常来自成本较低但相对容易故障的设备集,因此故障的发生已经成为一种常态。面对频繁的设备(即存储节点)故障事件,存储系统通常采用数据容错技术来保证存储数据的高可靠性和可用性[2-3]。

多副本技术是分布式存储系统采用的最简单的冗余方法[4]。然而,一份文件有多个副本,使得存储开销呈倍数增加。因此,牺牲更多的存储空间来换取存储数据的可用性,在海量数据生成的今天并不可靠。作为替代冗余技术,纠删编码在获得相同存储数据可靠性的情况下,比多副本技术节省更多的存储空间[5-7]。因此,纠删编码技术已经在许多大规模分布式存储系统中得到了应用,比如Google的ColossusFS和Facebook的HDFS-RAID[8]都部署了RS (reed-solomon)码[9-10],并分别将存储冗余降到了1.4倍和1.5倍,相比于三副本技术的3倍有着更强的优势。

然而,传统的纠删码方案比如最大距离可分离(maximum distance separable,MDS)[11-12]和喷泉码(fountain code,FC)[13-14],在处理故障节点修复问题时,需要访问多个可用节点数据并传输,不可避免地要消耗大量带宽资源,而分布式存储系统的带宽资源却很稀缺。为了解决这一问题,Dimakis等人将网络编码部署到分布式存储系统中,提出了再生码 (regenerating codes, RCs),降低了存储空间开销和故障修复的带宽资源开销[15]。之后Rashimi等人在这个基础上进一步提出了最小存储再生码 (minimum storage regenerating codes, MSR)和最小带宽再生码 (minimum bandwidth regenerating codes, MBR),分别实现了存储开销最小和带宽开销最小的目的[16]。MSR码和MBR码虽然都能有效地完成故障节点的修复工作,却会产生较高的磁盘I/O开销(即节点修复过程需要访问的可用节点数量)。因此,一些学者在纠偏码中引入了局部性的概念[17-19],并提出了相应的编码方案,其中最著名的就是局部可修码(locally repairable codes, LRCs)[20-22]。更准确地说,局部性被定义为需要访问以重建故障符号的其他符号数量。为了减少带宽消耗,系统通常期待一个低的局部性。然而,LRCs码的不足之处在于其构造比较复杂,在大规模分布式存储系统当中灵活性不高。

可修复喷泉码(repairable fountain codes, RFC)是文献[23]提出的分布式存储系统容错代码的一个新编码方案。与LRC码类似,RFC也有着较低的修复局部,另外同时兼备喷泉码的诸多优点:系统性、无率性、低编译码复杂度等。由于其在平衡存储开销和修复带宽方面的潜力,吸引了越来越多的研究兴趣。在文献[24]中,作者设计了一种安全的RFC,通过在消息中附加随机符号并通过Gabidulin码进行预编码来实现安全。考虑到多层异构存储网络中的数据缓存问题,在文献[25]中，作者设计了一种具有不等修复局部性的RFC,可以进一步降低不同边缘区域的整体通信开销。Baik等人[26]提出了一种局部改进RFC,通过逐项抽样和行丢弃来构造生成矩阵,从而实现在不降低译码性能的同时降低修复局部性。然而,对于RFC来说,为了保证译码的成功率,在传输编码包的同时需要将对应的生成矩阵进行传输,这就产生了额外的带宽资源消耗。传统喷泉码的每一个编码符号也都需要携带相应的邻居信息,这些信息随着消息符号的增加而非线性增加。这意味着会额外消耗带宽和存储资源。综上所述,研究新的RFC方案,减少分布式存储系统不必要的带宽开销具有重要意义。

在解决传统喷泉码或因传输编码生成矩阵而产生的额外高传输带宽开销问题上,已有学者研究了多种解决方法。文献[27-28]提出了基于熵编码的LT(luby transform)码生成矩阵压缩算法,在保持LT码性能的同时,大大减少了数据流量。文献[29]提出了一种模拟喷泉压缩传感(analog fountain compressive sensing, AFCS)方法来实现二进制稀疏信号的稀疏恢复。在文献[30]中,作者提出了一种新的递减冗余方法来压缩喷泉码源,实现无损解码。在文献[31]中,为了获得线性时间复杂度和竞争性能,提出了一种基于Raptor码的通用变长无损压缩算法。

受RFC和压缩算法的启发,基于改进的稀疏矩阵压缩存储算法提出了一种新的RFC编码结构。与非系统喷泉编码不同,RFC由于其系统形式而具有更好的可压缩性。在提出的方案中,编码包的邻域信息被建模为序列,并以生成矩阵的列为单位进行无损压缩。除此之外,还提出了一个新的性能指标—有效吞吐量来分析该方案的性能。在保留RFC的编码性能前提下,该方案可以有效减少故障节点修复和源文件恢复时因为生成矩阵的传输带来的额外数据传输量。

1 RFC及矩阵压缩存储模型

1.1 RFC的构造

RFC是Asteris等人[23]为了解决分布式存储系统可靠性问题所提出的容错编码方案。RFC拥有多个优点,包括系统性、稀疏性、近MDS性、逻辑局部性以及无率性。其中系统性对于分布式存储系统来讲至关重要,因为它表示可以在不需要解码操作的情况下读取到源文件信息,避免了更多的带宽资源消耗,符合目前许多分布式存储系统应用的实际需求。近MDS性是另外一个有利于高效下载数据的属性,表示当选择(1+ε)k个编码符号时可以高概率译码源信息,其中ε>0。对于逻辑局部性,表示修复一个故障节点需要访问的节点数为d(k)=C(lgk),其中C是常数。

原始文件被分成k份,并且用U=(u1,u2,…,uk)表示k个信息符号,其中U是有限域Fq上的k长信息符号序列。随后对信息符号进行k×n大小的生成矩阵G编码操作之后得到n个编码符号序列V=(v1,v2,…,vn)。需要注意的是,n个编码符号当中前k个编码符号是信息符号的副本,这也就表示编码符号为系统符号与校验符号的集合。通过下面的几个步骤可以得到余下的校验符号vj,j=k+1,k+2,…,n。

步骤 1依次独立、均匀地从k个信息符号中随机选择d(k)个信息符号;

步骤 2针对步骤1中选取的每一个消息符号,在有限域Fq当中随机地为其选择一个对应的系数进行加权;

步骤 3完成步骤2工作之后,将加权之后的消息符号进行线性组合,最终得到校验符号。

因此,通过重复上述步骤1～步骤3的过程,即可将余下的校验符号全部生成。在前面的假设中,已知向量u表示信息符号向量,则ui表示第i个信息符号,ui是有限域中的元素。用向量v表示编码符号向量,vj表示第j个编码符号,则其生成表达式可以表示为

vj=uG(j)=∑ωijui,j=k+1,k+2,…,n

(1)

式中:G(j)表示生成矩阵G中的第j列元素;ωij表示第j个编码符号,在选择第i个信息符号时对应的系数。其编码过程用图1来表示,为了统一表示,将编码符号中的前i个用来表示系统符号。

同时,也可以利用矩阵的形式表示其编码过程,则RFC系统形式的生成矩阵可以表示为G=[Ik|P],其中Ik是k阶的单位矩阵。生成矩阵如图2所示。

在图2中,生成矩阵的每一列表示一个编码符号,单位矩阵Ik反映编码符号中的系统符号部分,P对应的是其中的校验符号。生成矩阵的具体生成过程如下:

步骤 1首先生成一个k×n的矩阵G,其中包括两个子矩阵,即k×k方法的单位矩阵Ik和k×(n-k)方法的全零矩阵;

步骤 2根据前面生成校验符号vj的过程,记录选取的d(k)个信息符号的序号以及对应的系数;

步骤 3对矩阵G中的全零子矩阵进行操作,将其第j列中d(k)个序号对应行的零元素替换成相应的系数,其中j=k+1,k+2,…,n;

步骤 4重复步骤2和步骤3,直到矩阵G中的n列全部生成完毕。

从图3中可以看出,每一个校验符号最多由d(k)个信息符号加权组合而成。因此,一个校验符号和对应的d(k)个信息符号组成一个局部组。表示在局部组中修复单个故障节点只需要访问本组中d(k)个剩余符号即可。另外,根据编码规则可知,每个信息符号都有多个不相交的局部组,这使得系统符号的修复可以通过访问其中任意一个不相交的局部组来实现。

1.2 稀疏矩阵压缩存储

对于稀疏矩阵,非零元素很少且随机出现。在许多实际应用中,稀疏矩阵中零元素的存储和计算是没有意义的。为此,提出了稀疏矩阵压缩技术来解决这一问题。该技术对矩阵的行/列中的非零元素进行运算,避免了由零元素引起的不必要的运算成本。对稀疏矩阵的列进行操作时,即压缩列存储(compressed column storage, CCS),提取矩阵中所有非零元素,并按列行顺序存储在一维数组中。同时,提取每个非零元素对应的行位置并保存到另一个一维数组中。因此,还有一种压缩行存储(compressed row storage, CRS)算法,该算法对矩阵的行进行操作。从可修复喷泉码的生成矩阵G来看,每一列相当于一个传输的数据包。因此,为了保持可修复喷泉码的性能,提出了一种基于改进压缩列存储算法的可修复喷泉码结构来实现数据压缩。

1.3 相关参数定义

为了更全面地分析所提出的方案,本文给出了几个定义。

定义 1压缩比(η):表示压缩后的数据量与压缩前的数据量的比值;

定义 2单节点修复有效吞吐量(γrepair):表示修复单个故障节点所需传输的数据量;

定义 3成功解码有效吞吐量(γdecoded):表示成功解码源文件所需传输的数据量。

2 新型RFC的构造设计

为了进一步降低分布式存储系统的带宽和存储资源开销,本节提出了基于改进压缩列存储算法的新型RFC (RFC based on improved compressed column storage, ICCS-RFC)的构造方法,该方案通过压缩编码符号所携带的邻居信息来进一步减少传输的数据量。改进压缩列存储算法的思想源于压缩列存储算法与码本压缩算法的结合,后者通过利用M个二进制位来表示非零元素的位置来实现。

根据RFC生成矩阵的特点和改进压缩列存储算法的原理,提出的方案应遵循以下几个原则:

(1) 生成矩阵的稀疏性原则。该方案将提取生成矩阵中少数非零元素的值和位置作为有用信息,并将其视作提出方案的信息源进行编码操作。

(2) 编码符号的独立性原则。在ICCS-RFC方案的编码过程当中,每个编码符号的生成是相互独立的。因此,压缩操作应该围绕每个编码符号完成,即在生成矩阵的列上执行,以保持可修复喷泉码的特性。

(3) 最大度值原则。为了达到压缩的目的,存在一个最大的度值来保证存储信道上传输的邻居信息的冗余度最小。

2.1 压缩模型的构造

首先,建立一个压缩模型来提取生成矩阵G的非零数据。如图3所示,描述了n=10,k=8,d=2时，可修复喷泉码用于压缩模型的邻域信息提取的示例。

根据压缩模型可知,生成矩阵G中的非零元素被提取出来后存储在一维阵列Val中,元素对应的位置被存储在另一个一维阵列Row中。完成生成矩阵G的非零元素提取操作后,利用码本压缩技术,对提取出来的信息进行编码。令Lj,j=1,2,…,n表示非零元素的数量,Dmax表示非零元素数目的最大值,称为最大度值。利用M二进制比特表示提取的邻域信息。根据最大度值原则,可以得到定理1如下。

证毕

2.2 ICCS-RFC方案的编码过程

根据上述压缩模型的设计方案,ICCS-RFC方案的编码过程可以描述如下。

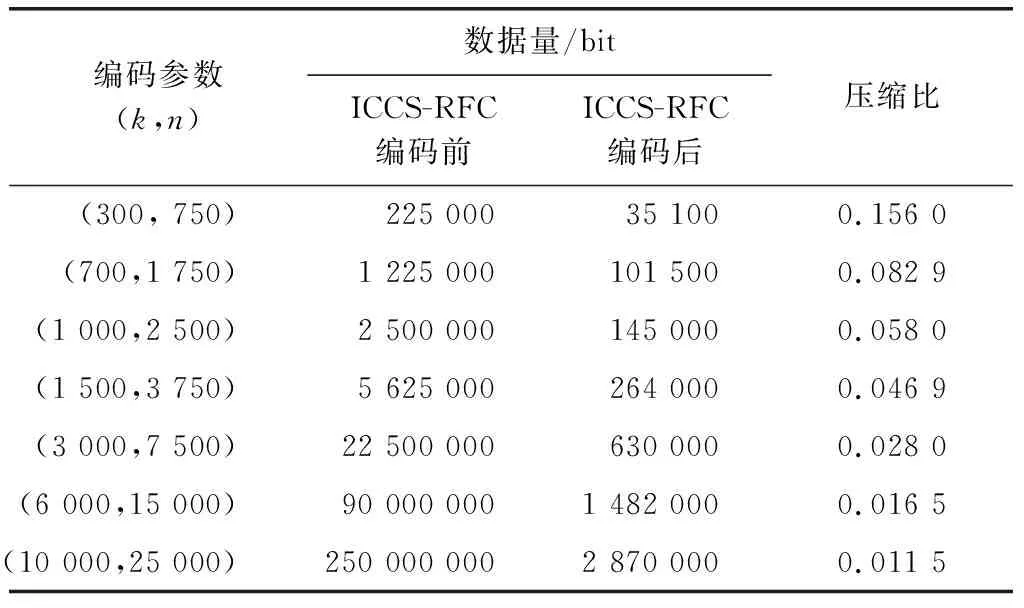
步骤 1k个信息符号U=(u1,u2,…,uk)通过(n,k)可修复喷泉码编码成n个编码符号V=(v1,v2,…,vn),根据第1.1节给出的生成矩阵的生成过程,得到生成矩阵G。然后计算出最大度值Dmax,并与生成矩阵当中的度值d(k)比较,若d(k)

步骤 2利用改进的压缩列存储算法对步骤1中提取的邻域信息进行压缩处理,然后用压缩之后的邻域信息序列替换原来的邻域信息序列,并将其与对应的编码符号进行组合传输;

步骤 3重复上面的步骤,直到完成n个编码符号的传输。

2.3 有效吞吐量的分析

令源文件的大小为F比特,将源文件等分成k份,则每一份信息包的大小为α=F/k。不失一般性,假设每个存储节点所存储的数据包数量为α。为了全面分析有效吞吐量,考虑两个场景:单故障节点修复和源文件下载。

2.3.1 单故障节点修复场景

从第1.1节可知,一个校验符号及其对应的消息符号组成一个局部组。因此,当出现单节点故障时,通常在对应的局部组中进行节点修复,即通过访问局部组中余下的节点来实现故障节点修复。因此,可以计算修复单个故障节点的有效吞吐量。需要注意的是,因为局部组包含的节点包括消息节点和校验节点,所以需要分别考虑,具体计算结果如下所示。

对于提出的ICCS-RFC编码方案：

(2)

对于RFC编码方案：

(3)

式中:d(k)表示修复局部。从式(2)和式(3)可以知道,当一个系统符号丢失时,需要在局部组中访问d(k)-1个系统符号以及一个校验符号进行丢失数据的重建。当一个校验符号丢失时,需要链接局部组内d(k)个系统符号进行丢失数据的重建。因此,必需的数据包传输量和对应的邻域信息量相加,即可得到有效吞吐量。

2.3.2 源文件下载场景

为了实现高概率的成功解码,需要下载一组(1+ε)k编码符号,其中ε>0。因此,成功解码所需的有效吞吐量可计算如下。

对于提出的ICCS-RFC编码方案:

(4)

式中:d1表示接收到的度值为1的编码符号数量。因此,在接收到的编码符号中度值为d(k)的数量为((1+ε)k-d1)。

对于RFC编码方案:

(5)

式中:(1+ε)kk表示接收数据包的邻域信息的数量;α(1+ε)k表示接收数据包的数量。

3 系统仿真与结果分析

本文仿真平台是Win10系统,CPU为2.50 GHz,内存是8 GB,采用Matlab 2014a软件仿真。

在这一部分中,通过实验结果分析了ICCS-RFC方案的性能,并在有效吞吐量方面与文献[9]中的传统RFC方案进行了比较。具体计算了不同消息符号长度k下改进的压缩列存储算法实现前后的数据传输量,数值结果如表1所示。

表1 ICCS-RFC编码方案的结果

对于表1,度数d(k)=Clg(k),设置C=1。第2列表示在实现ICCS算法之前需要传输的邻居信息量,第3列表示ICCS算法实现后需要传输的邻居信息量。

在表1中,随着消息长度k的增加,两种方案的邻居信息量都急剧增加。从实验结果可以看出,在实现ICCS算法之前,要实现高概率的成功解码,邻域信息量是巨大的。经过ICCS算法压缩后,邻域信息量明显减少。当k=700时,压缩比降低到0.1以下,这意味着邻域信息量被压缩了90%。而且,可以看到,k值越大,压缩比的降低越小。因此,该方案可以显著减少传输数据量,节省带宽资源。

从图4(a)可以看出,对于不同的消息长度k,ICCS-RFC方案在修复单个故障节点时有着更小的有效吞吐量,比如,当k=2 000时,RFC方案的有效吞吐量为4.406×104,ICCS-RFC方案的有效吞吐量仅为250左右。另外,在图4(b)中,可以看到,在源文件下载过程中,ICCS-RFC方案的压缩效果也非常显著。当k=2 000时,ICCS-RFC方案的有效吞吐量为1.826×105,与RFC方案的4.401×106相比,需要传输的数据量明显减少。因此,本文提出的方案在进一步降低带宽资源开销方面具有明显优势,特别是在单故障节点修复的场景下。

在图5中可以看到,在两种场景中,随着消息长度k的增长,压缩比也是随之降低,但降低的速率逐渐减小。尤其在单故障节点修复场景中,当k>1 000时,ICCS-RFC编码方案将压缩比下降到了10-3个数量级。所以,可以看出,ICCS-RFC方案能够明显降低存储信道的传输冗余,尤其是在单故障节点修复场景中。

在图6中,基于熵编码的LT码相关参数设为(c=0.1,δ=0.01),随着消息长度k的增加,这两种方案的压缩比都下降。当ICCS-RFC方案中度值包含的常数C=2时,该方案的压缩比大于基于熵编码的LT码。当该参数C取1和0.7时,该方案的压缩比则要低于基于熵编码的LT码。综上所述,参数C在ICCS-RFC方案中起着重要作用。因此,选择合适的C值是保证方案性能的关键。

4 结 论

本文提出了一种基于ICCS算法的新型可修复喷泉码结构。理论分析和仿真结果表明,该方案能显著降低带宽资源开销,尤其是在修复单个故障节点时。与传统可修复喷泉码方案相比,提出的ICCS-RFC方案在节省带宽资源方面具有更好的性能。未来,我们将重点研究ICCS-RFC方案在异构分布式存储系统中的应用,以达到信息保护和通信成本节约的目的。