受融资影响的项目组合选择研究

李星梅, 王 丽, 赵秋红

(1.新能源电力与低碳发展研究北京市重点实验室(华北电力大学)，北京 102206; 2.北京航天航空大学 经济管理学院，北京 100191)

0 引言

随着市场经济的快速发展，项目投资涉及的领域日益扩大并呈现出多元化趋势，致使可供企业选择的项目数量急剧增长。企业为了保持自己竞争力，完成其战略目标，决策者需要在众多候选项目中进行取舍。如何在不违背各种关键约束的前提下，从众多待选项目中选出最具有价值的几个，实现企业的战略目标，通常被定义为项目组合选择问题(Project Portfolio Selection Problem，简称PPSP)[1]。自项目组合选择问题最早由Lorie和Savage[2]提出后，就在管理科学领域吸引了极其广泛的关注，并被应用到研究与发展[3]，信息系统与信息科技[4]，创新型[5]等投资决策领域中。

项目的执行需要一定的时间。根据执行周期的不同，研究者将项目的规划期分为单时间段和多时间段两种类型。目前，多时间段项目组合选择问题的文献较多，但根据我们的检索，针对项目组合选择中资金问题的研究相对较少。而在企业实际运营中，资金对企业的项目选择会产生重要影响，因此将二者结合考虑具有重要的现实意义。在项目的执行过程中对于资金分配问题，Servakh和Sukhikh提出收益再投资理论。基于这一理论，文献[6,7]考虑了再投资策略在项目组合选择问题中的应用，并且考虑了项目资金需求的紧迫性，进而对资金进行合理分配。但在以上研究中，只考虑了企业现有资金的投入，没有对资金的具体来源情况进行说明，同时资金短缺的情况被忽略。显然，这样不符合企业的实际运营。文献[8]在对项目组合选择中资金分配时，考虑了资金的定量约束。其算例结果显示，企业投入的定量资金远大于实际需要的金额，造成部分资金没有得到充分的利用。而文献[9]允许再投资策略在灵活的时间范围内进行应用，打破以往投资时间范围一直被视为固定区间的假设。通常，企业资金的来源主要包含内部资金和外部资金。然而，在以上项目组合选择的研究中关于资金问题的来源只局限在内部资金，没有考虑资金限制下进行融资的现实因素。

事实上，资金受到限制时如何获取外部资金是企业经常遇到的问题。在企业实际运营中，为了应对资金不足问题，会通过多渠道进行融资，进而使企业的资源配置得到优化，提高企业的经济效益[10]。因此，有关于债权和股权的融资结构也受到了学者们广泛关注。其中，李涛等[11]研究发现，现金流量充足的上市企业更偏向使用股权融资方式来获取外部资金。而邬文瑾[12]指出对于项目尚未形成资产的企业更倾向于使用债权融资。针对本文中现金不足且尚未形成资产的企业情况，使用债权融资更符合现实情况。因此，本文仅从债权融资角度研究项目组合选择问题。

由于银行贷款具有相对较低的成本和期限灵活的优势，目前已经成为我国企业的第一大债权融资来源[13]。因此，本文在项目组合选择问题中仅考虑银行贷款这一类几乎适用于任何企业且应用最为广泛的外部融资方式，使得研究更具有现实意义。目前，许多文献已经在项目组合选择问题中考虑了融资因素，如文献[14,15]中假设企业在每期期初有固定的外部资金投入，确保企业正常运营。文献[16]提出对外部融资需求量进行预测和分析，进而确定合适的融资金额。在以往的项目组合选择研究中假设外部筹资具有确定性的，即企业一定能够获得融资且金额多为固定值。与以上文献不同，本文在融资的过程中，将项目风险对投融资企业的影响结合考虑。根据项目执行风险的高低，确定融资企业能否获得资金支持。同时，在未来充分考虑利率市场化的大背景下，融资代价会根据项目风险程度不同，执行不同的利率浮动标准，风险越小，利率越优惠[17]。在满足融资条件下，企业需要对融资代价与项目执行带来的收益进行权衡，进而选择最优的项目组合方案。

综上，本文考虑了融资影响下的项目组合选择。具体的创新之处包括两点：其一，根据现实情况，本文拓展了传统的项目组合选择模型中资金预算约束的表达式，采取债权融资方式，保证企业不会错失最有价值的投资。其二，融资代价对项目组合经济性的影响被引入到模型中，首次讨论了贷款利率及风险管理对项目组合选择的影响。算例结果显示，考虑融资策略有效提高企业收益，对企业的生存与发展具有借鉴意义。

1 模型介绍

1.1 符号说明

本部分对模型中使用的参数及变量介绍如下：

(1)集合

v：待选项目集合，其中项目为j∈v,j=1,2,3,…,n；

Λ：计划期内各时间段的集合，时间段t∈Λ，t=1,2,3,…,T,时间段t开始于时点t-1而终止于时点t。

(2)参数

i：基准折现率；

N：在整个计划期内允许选择项目的最大数量；

Mt：时间段t内允许执行项目的最大数量，t∈Λ；

kj：执行整个项目j的成本，j∈v；

bj：完成整个项目j后可以获得的收益，j∈v；

αjt：项目j在时间段t内允许执行的最小比例，j∈v,t∈Λ；

βjt：项目j在时间段t内允许执行的最大比例，j∈v,t∈Λ；

L(t)：企业在时点t处可借得的贷款的最小值，t∈Λ；

U(t)：企业在时点t处可借得的贷款的最大值，t∈Λ；

ρ：企业每次进行银行贷款时，所需要支付的交易费用，与每次贷款的金额无关。

(3)变量

Zj：0-1变量，Zj=1表示项目j被选择，否则为0，j∈v；

xjt：半连续变量，表示项目j在时间段t内所执行的比例，xjt∈0∪[αjt,βjt]。若xjt=0，表示项目j在时间段t内没有被执行。若xjt∈[αjt,βjt]，表示项目j在时间段t内执行的最小比例是αjt，最大比例是βjt,j∈v,t∈Λ；

yjt：0-1变量，yjt=1表示项目j在时间段t内被执行，否则为0，j∈v,t∈Λ；

E(t)：半连续变量，表示时点t处企业使用的外部资金(本文外部资金指银行贷)，t=0,1,2,…,T-1，E(t)∈0∪[L(t),U(t)]；

I(t)：时点t处企业使用的其他自有资金，t=0,1,2,…,T-1；

ut：0-1变量，当且仅当企业在时点t处选择贷款时ut为1，否则为0，t=0,1,2,…,T-1；

H(t)：连续变量，表示企业在时间段t内实际投入的全部资金量，t=0,1,2,…,T-1；

Vt：在时间段t内执行的所有项目总风险，t∈Λ；

rt：离散变量，表示银行根据企业时间段t内投资计划的风险情况制定的贷款利率。

1.2 问题描述

对于每一期的可用资金，既包括企业筹措的外来资金，也包括企业的内部资金。本节将分别针对这两种情况进行讨论：

(1)外来资金

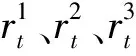
其中a1，a2，a3为评定风险等级的阈值。每超过某一阈值，企业投资计划的风险等级就会提升一级。

除去贷款利息这一借款所需要付出的代价，本文还考虑了每次贷款时需要支付的交易费用。而企业贷款为0的情况又可分为两类：一类是企业在当期执行的项目风险过高，银行拒绝贷款，不会产生相应贷款利息，故不予考虑；另一类是企业满足贷款的条件但并不需要外来资金，故而主动选择在该时点不贷款。所以，考虑企业满足贷款的条件但并不需要外来资金的情况，只需建立E(t)和ut间的关系模型。其关系模型如下：

(1)

(2)内部资金

对于内部资金，又可以进一步细分为先前所执行项目获得收益再投资及当期投入的其它自有资金。对于其他自有资金，假设在起始点企业决定投入的自有资金为I(0)，这笔资金将全部用于第一时间段内项目的执行。为了核算的方便，考虑到资金的时间价值，之后的每期(t=1,2,…,T-1)期初有I(t)的其他自有资金流入，期末会有一笔等值但非等额的资金I(t+1)=I(t)(1+i)作为现金流出。根据这一假设，每期投入与回收的其他自有资金是等值的，可以相互抵消，故不需要在目标函数中体现。

结合问题描述中(1)和(2)考虑再投资部分。本文假设上期结余的全部资金均可以用于下一期的投资。为了准确地计算每期的结余资金，以时间段为例，对每一期可能发生的多笔现金流进行梳理。

首先，在t-1时点处最多发生三笔现金流入，一是在t-1时点处结余的资金，二是可能发生的银行贷款，三是企业当期决定投入的其他自有资金。接着，假设t时间段内有项目被执行，将有现金流出用于t时间段内执行项目花费的成本。如果t-1时点处进行了银行贷款，将会产生二笔现金流出，即为了贷款而支付的交易费用和偿还银行的本息。同时，t时点其他自有资金退出生产。剩余的资金即t时点处结余的全部资金。特别地，本文假设0时点处结余的资金为0。图1更加直观地显示了上述过程。

基于以上考虑，可以推导出t时点处企业可用于投资的最大额度为公式(2)所示:

(2)

1.3 资金预算约束

为了提高资金的利用效率，避免资金不足或资金过剩的情况，本文假设决策者在每一期的预算约束中追求的是资金的使用与预算的平衡，且使用的资金不超过当期期初投入全部资金的最大数额。所以，资金预算约束的表达式如下:

(3)

(4)

通过(4)式，保证了当期投入的全部资金可用于本时间段的项目执行，又不使得全部的可用资金都在本期内被占用，故而提高了资金的使用效率。

2 考虑融资的项目组合选择模型

本文构建的考虑融资的项目组合选择模型如下所示:

(5)

s.t.(2)～(4)

(6)

(7)

αjtyjt≤xjt≤βjtyjt,j∈v,t∈Λ

(8)

(9)

接下来对其他非预算约束及目标函数进行说明：(5)是目标函数，表示企业的目标是最大化项目组合的净现值；(6)与(7)是指标约束，用于限制在计划期内的每一时间段允许执行项目的最大数量及整个计划期内可选择项目的最大数量；(8)为可打断约束，用以限制计划期内的每一时间段执行项目的比例；(9)表示对于任意一个待选项目，要么不被选择，但如果被选择就必须在计划期结束前完成。

3 模型求解

本文构建的项目组合选择模型是一个混合整数线性规划模型，属于NP-hard问题。接下来将通过以下3个命题，给出所有的非线性项完全等价的线性项，降低模型求解难度。

rt与Vt间的非线性关系将会对模型的求解造成困难。为了克服这一难题，给出如下的命题1。

命题1银行在时间点t内制定的贷款利率rt的非线性形式为

与以下的线性表达式等价：

(10)

接下来考虑企业满足贷款的条件但并不需要外来资金的情况。因为命题1已经通过令E(t)=0约束了第一种不发生贷款的情况，故而此时只需要对E(t)和ut间的关系进行建模即可。考虑如下命题:

命题2E(t)∈0∪[L(t),U(t)],t∈Λ，与以下不等式：

L(t)·ut≤E(t)≤U(t)·ut，t∈Λ，其中

(14)

等价。

证明参见文献[10]。

当ut被成功地建模后，就很容易计算每期的贷款交易费用。

最终，基于上述三个命题，所有的非线性项被等价线性项代替。原有目标函数等式(5)经线性化处理后与等式(17)等价，新的考虑融资的项目组合选择模型为:

(17)

s.t.(2)～(4)，(6)～(16)

4 算例分析

4.1 案例背景及相关数据

4.2 结果分析与场景对比

本小节中，通过求解本文构建的新模型进而分析其结果，并与传统的不考虑融资的项目组合选择模型进行对比,以证明新模型的有效性及合理性。

首先对表2数据进行说明。如第一阶段下的1(0.900)意味着项目1在第一时间段内执行了90%的比例，其他类似。从表中可以看出，企业共选择了5个项目，其中3个新能源项目，2个传统项目。从表3中的投资风险情况来看，只要企业在当期进行了银行贷款，那么其风险等级一定是最低的一级，而新能源项目较低的风险使其更加容易被企业选择。再观察每期的资金利用情况发现，对于银行贷款，企业仅选择在第1与第2阶段使用。而对于其他自有资金，因为不用偿还贷款利息，故而会被尽可能利用。

表2 新模型的最优解

表3 新模型规划期内资金利用情况

接下来与传统的仅使用内部资金的项目组合选择模型进行对比，即在不考虑融资情况下，我们仍然采用先前的参数，但令每一期的贷款金额为0(Et=0,t∈Λ)，求解结果如表4所示。

表4 传统无融资下的最优解

从表4中可以看出，在传统的仅使用内部资金的情况下，企业选择了4个新能源项目及1个传统项目。这是因为新能源项目相较于传统项目所需要的运营成本更低，故在没有更多资金的情况下，企业被迫选择低利润但同样低成本的项目，最终企业获得的净现值为16.536，相较于本文提出的新模型19.621低了3.085单位。

最终，算例结果分析得到的结论如下：

(1)相较于传统的项目组合选择模型，本文提出的考虑融资的新模型能够为企业带来更多的利润，因而更具有优势；

(2)对于银行贷款的使用，企业更加倾向于整个计划期的前期使用。这是因为随着时间的推移，可用于再投资的资金逐渐增多，导致企业放弃银行贷款；

(3)对于高风险且高收益的项目，企业更加倾向于整个计划期的后期执行。这是因为高风险项目执行成本较高，但后期资金积累增加，企业可以不借助银行贷款，获得高收益的同时避免高风险带来的利息。

4.3 敏感性分析

从4.2节中的算例结果可以看出，银行贷款体现了企业在高风险项目带来的高利润与还款利息间的权衡，及新能源项目的低风险与传统项目的高收益间的权衡。因此，有必要对模型中的一些关键参数进行敏感性分析，观察不同参数对企业决策，尤其是资金使用情况的影响。分析如下所示：

4.3.1 贷款利率的敏感性分析

在贷款利率的敏感性分析中，分别令三种风险等级下的贷款利率各自增加0.02和减少0.02，再重新对模型求解，得到的每一期资金使用情况如下：

表5 贷款利率增加0.02后的资金利用情况

表6 贷款利率减少0.02后的资金利用情况

通过两表的对比可以看出，贷款利率设定得越高，企业越不倾向于贷款。因为贷款利率越高，企业需要偿还的利息也就越多，于是企业宁可选择执行低成本低利润的项目也不愿过多贷款。另一发现是：无论银行贷款利率上升或下降，但企业的投资计划依然保留了低风险的特征，将每一期执行项目总风险的等级控制在最低级即选择最低的贷款利率，这一现象也说明融资利率管控及风险评估对项目组合决策的影响显著。

4.3.2 其他自有资金最大使用量的敏感性分析

分别将其他自有资金最大使用量减少为10和增加到30(原算例为20)，观察资金使用情况如下：

通过对比表7和表8可以发现，其他自有资金使用量的变化对银行贷款的影响显著。由于自有资金与银行贷款都用于项目的执行，因此自有资金的增大必然导致银行贷款需求量减少。此外，使用自有资金不用考虑偿还银行贷款利率，且有利于再投资策略发挥作用，这无疑削弱了企业对银行贷款的需求。

表7 其他自有资金最大使用量减少到10后的资金利用情况

表8 其他自有资金最大使用量增加到30后的资金利用情况

5 结论

在全球竞争环境下，企业的投资机会越来越多，投资所需资金来源也日益丰富，同时项目投资风险可能对项目组合的经济性造成不同影响。基于这一启示，本文构建了一个考虑融资的项目组合选择模型，允许企业根据实际需求，灵活地调整每一期的资金预算。为了避免资金被过度占用或资金不足的情形出现，本文允许企业在综合考虑成本收益、项目风险及贷款利率的情况下，合理地选择贷款的金额，实现资金利用效率的最大化。

未来还有以下方向可以拓展。举例来说，当前PPP模式是非常火热的一种项目经营模式，也是融资的重要方法之一。如何考虑这类融资方式下的利益分配问题，进而构建新的预算约束模型需要进一步地研究。