带缓冲串行生产系统预防性维护建模及运行参数优化研究
2022-02-16周宏明张祥雷王素芬黄沈权
周宏明, 高 顺,2, 张祥雷, 王素芬, 黄沈权
(1.温州大学 机电工程学院,浙江 温州 325035; 2.浙江安防职业技术学院,浙江 温州 325016)
0 引言
随着现代生产线日益朝着大型化、集成化、智能化方向发展,依靠车间维护人员经验的传统维护方式已经很难满足实际生产要求。合理的维护计划,不仅能确保生产线的可靠性,而且能最小化维护成本,从而提升企业综合竞争力。
目前,关于生产线可靠性问题已有大量国内外学者研究。Khatab等[1]在生产系统的维修决策模型中考虑了交替任务和预定休息时间对预防性维护周期的影响。Hong等[2]采用copula函数模拟单个设备的随机衰退过程,并基于最小期望成本准则和随机占优决策法则求解多设备生产系统的最佳维护策略。Lu和Zhou[3]提出了多级制造系统的机会维护决策模型,模型中考虑了上下游设备间的退化相关性。Hou和Jiang[4]以多单元串行生产系统为研究对象提出了一种机会维护策略。Seidgar等[5]为解决两阶段装配生产车间调度问题,提出了一种基于双目标混合整数规划的预防性维护模型。Zhou等[6]以最小化系统维护成本为目的,提出了一种用于基于时间窗的预防性维护模型。胡瑾秋等[7]提出一种综合分析多种参数的机会维护策略。此外,为了保障生产线产能,一些学者在对多机生产系统进行可靠性研究时考虑了缓冲库存决策问题。
Lee等[8]建立了生产线可靠性评估模型,模型中考虑了缓冲库存中在制品的等待时间。王林等[9]提出一种基于预防性维护决策方法的缓冲库存分配优化模型。余佳迪和周炳海[10]基于带缓冲串行生产系统提出一种预防性维护决策模型。Nahas和Nourelfath[11]基于带缓冲串行生产系统维护成本最小化,提出一种预防性维护策略。M.Zandieh等[12]采用启发式算法基于维护时间提出最小缓冲库存模型。Oliver等[13]基于离散时间提出生产系统缓冲库存优化方法。张良安等[14]针对自动化生产线提出一种以生产线最大可用度为目标缓冲区容量分配。
通过以上文献分析可知,对生产线的可靠性研究大都集中于系统的可靠性评估与维护策略制定,忽略了各执行单元的运行参数、性能特性及不同维护模式对整条生产线可靠性的影响。为此,本文以串行生产线系统为例,将其生产线执行单元为研究对象,分析了执行单元可靠度与生产线运行参数的关系、执行单元可靠度与维护策略的关系模型、执行单元可靠度与在制品缓冲库存的关系,建立了以生产线维护成本最小、有效运行速度最大及缓冲库存最小为目标的维护决策模型,并采用启发式算法求解最佳维护决策。
1 问题描述
目前制造行业中所采用的生产线普遍是根据产品的工艺路线将多个设备通过一些机构串联而成,我们将这些生产设备称为执行单元。由于执行单元停机维护将严重影响生产线产能,若在执行单元间设置缓冲库存单元将降低对生产线产能的影响。在生产线运行过程中,生产线的可靠性及产能,是通过设置合理的运行速度和缓冲库存量来保障。此外,维修频率的合理性不仅可以提升生产线可靠性的同时又能使生产效益提高。本文以最大化有效运行速度、最小化维护费用及最小化缓冲库存为优化目标,研究多单元串行生产线系统可靠性与运行速度和缓冲库存之间的影响。
1.1 运行描述
一条由n个执行单元和n-1个缓冲库存单元组成的生产线,如图1所示。以执行单元UA(i)和缓冲库存单元UB(i)为例,执行单元UA(i)的有小修、预防性维护、更换三种维护方式,以I,P和Q分别表示。其中小修不改变可靠性,只实现正常运行功能,预防性维护影响可靠度,并非恢复如新,更换可使系统役龄回退,恢复如新,分别用TMI,TMP,TMQ来表示三种维护活动。缓冲库存单元UB(i)的库存量B(i)用于保证当执行单元UA(i)进行维护活动,下游执行单元UA(i+1)不维护时可连续生产。
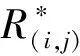
在一个订单周期内,分别用NI(I)、NP(i)、NQ(i)代表执行单元UA(i)进行小修、预防性维护和更换的次数,令预防性维护活动进行NB次后执行单元进行一次更换活动。
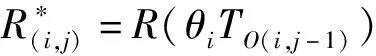
在一个订单周期内,执行单元UA(i)维护总成本为Mc(i);执行单元UA(i)有效运行速度为Vr(i),表示在一个订单周期内执行单元UA(i)在可靠度约束下的工作效率;缓冲库存单元UB(i)缓冲库存量为B。
对于带缓冲串行生产线,其运行速度为v。则生产线的维护决策过程可描述为:在第j次工作期,生产线以速度v运行TO(j)时间,在工作期间执行单元被小修数次,随之其可靠度也下降,且执行单元的可靠度满足R(t)≤RT时,预防性维护满足预防性需求的单元执行,更换满足更换条件的单元执行;在此期间,其余执行单元依托其上游缓冲单元的缓冲库存以速度v继续进行生产;随后维护后的单元继续以速度v工作,依次循环,直至完成订单任务。
1.2 可靠度模型
影响生产线维护总成本MC的关键因素是生产线的维护时间,可靠度是影响维护时间的重要因素,而磨损是影响生产线可靠度的重要因素。在所有影响系统可靠度的因素中,磨损是对可靠度影响最大且不可避免的因素之一。此外,生产系统的运行参数是通过影响单元的磨损量进而影响系统可靠度的,因此本文用磨损作为衡量可靠度的因素,基于执行单元的磨损量变化建立可靠度模型。
1.2.1 磨损模型
执行单元磨损量模型为[15]:
ωi(t)=k·pξ·(lv)δ·t
(1)
(2)
1.2.2 可靠度模型
由磨损性质可知,执行单UA(i)磨损量变化与可靠度Ri(t)之间的关系符合正态分布,则可靠度Ri(t)可表示为[15]:
(3)
本文所研究的生产线是由多个执行单元和缓冲单元串联组成,因此,该生产线的系统可靠度R(t)为:
(4)
2 建立优化模型
2.1 维护成本模型
直接维护成本和间接维护成本是生产线上大体的两类维护成本。
2.1.1 执行单元与缓冲库存单元的维护成本模型
使用CI表示执行单元完成一次小修活动所需维护成本、CP表示完成一次预防性维护活动所需维护成本、CQ表示完成一次更换活动所需的维护成本、因维护造成的生产损失成本为CD,缓存单元单件库存存储成本为CB。
执行单元UA(i)在一个完整订单周期内,其直接维护成本MCT(i)可表示为:
MCT(i)=CI·NI(i)+CP·NP(i)+CQ·NQ(i)
(5)
其中,NI(i)、NP(i)、NQ(i)分别为一个订单周期内,执行单元UA(i)进行小修活动、预防性维护活动、更换活动的次数。同理,间接维护成本MCL(i)可表示为:
MCL(i)=CD·NP(i)+CP·NQ(i)+CB·B(i)
(6)
研究的执行单元UA(i)的磨损寿命变化过程服从正态分布,通过故障密度函数和式(3)可得到,执行单元的故障率为:
(7)
在订单周期内小修活动总次数为:
(8)
令执行单元UA(i)的预防性维护累计次数每次达到NR的整数倍时对其完成一次更换活动,则在订单周期内完成更换活动的总次数为NQ(i)=NP(i)/NR(i)。
2.1.2 生产线的维护成本模型
维护总成本为所有单元直接维护费用及间接维护费用之和MC为:

(9)
2.2 运行速度模型
用Vi表示一个订单周期内执行单元UA(i)的运行速度,在运行期间内该执行单元UA(i)的运行速度为v,在维护期因停机维护速度为0;一个订单周期内生产线在一个订单周期内的运行速度为V,由于在维护期进行停机维护的执行单元只是部分执行单元,那么其余执行单元可通过上游缓冲库存继续工作,即整体上生产线不进行停机且持续生产,因而在订单周期内生产线运行速度一直为v。
关于执行单元的运行过程为:
(10)
执行单元UA(i)在工作周期和维护周期的整个订单周期内的有效运行速度为Vr(i);基于工作周期和维护周期整个订单周期内生产线的有效运行速度为VR,执行单元UA(i)在一个订单周期内的有效运行速度为:
(11)
(12)
2.3 缓冲库存模型
无缓冲生产线在维护期必须停机进行维护,为了提高产能,在执行单元间设置缓冲库存,以保障下游不需要进行维护的执行单元继续正常生产。由n个执行单元和n-1个缓冲库存单元组成一条串联型生产线,令缓冲库存单元UB(i)的缓冲库存量用B(i)来表示。
以系统有两种状态的二级串联生产系统为例,其两种状态为:
状态1执行单元UA(i)和UA(i+1)都处于工作状态,且缓冲库存单元UB(i)空闲、执行单元UA(i+1)没有空闲;
状态2执行单元UA(i)进行维护,执行单元UA(i+1)处于工作状态,且缓冲库存单元UB(i)不为空闲、执行单元UA(i+1)没有空闲;
则在维护期TM(i)内,理论上当上游执行单元须停机维护而下游执行单元不需要维护时,能保证下游执行单元继续工作的缓冲库存单元UB(i)最小缓冲库存量为:
(13)
式中,τi+1是执行单元UA(i+1)的生产节拍;B(i,j)MIN=TM(i)/(τi+1)表示执行单元UA(i+1)正在加工产品数为0时缓冲库存单元UB(i)的缓冲库存量;B(i,j)MIN=TM(i)/(τi+1)+1表示执行单元UA(i+1)正在加工产品数为1时缓冲库存单元UB(i)的缓冲库存量。
生产节拍τ的计算为:
τ=Ta/Td
(14)
式中,Ta代表可用的工作时间,Td代表客户的需求量。在本文中Ta=TO,Td=v·TO,故生产节拍τ的计算:
τ=TO/(v·TO)=1/v
(15)
则缓冲库存单元UB(i)最小缓冲库存量为:
(16)
约束条件:
1)缓冲库存单元在订单周期内可靠且满足先进先出;
2)半成品运输到缓冲库存单元所需时间短,忽略不计;
3)当某执行单元UA(i)进入维护期时,其下游缓冲库存单元UB(i)库存一次性加满,不论缓冲库存是否被下游执行单元UA(i+1)消耗完都不在添加,直到该执行单元UA(i)再次进入维护期缓冲库存单元UB(i)的库存再一次加满;
4)缓冲库存单元中的半成品的质量等参数与生产线上对应生产该半成品的执行单元所生产半成品的质量等参数相同。
3 维护策略
3.1 建立优化目标模型
带缓冲串行生产线的优化目标模型分别为:
1)生产线的有效运行速度为:
(17)
2)生产线的维护成本为:
MC=ΣMC(i)→Min
(18)
3)生产线缓冲库存单元的库存量:
下游执行单元在上游执行单元维护活动完成前一直持续生产,则缓冲库存单元UB(i)库存量B(i)需满足B(i)≥B(i)Min,因此,库存量:
(19)
本文引入权重因子,取有效运行速度v(单位运行成本为1)、维护费用MC和和缓冲库存量BMIN(缓冲库存的单位成本为1)三个优化目标函数的权重和作为总优化目标函数采用加权求和法对多目标优化函数进行优化求解,多目标优化函数为:
(20)
约束条件:
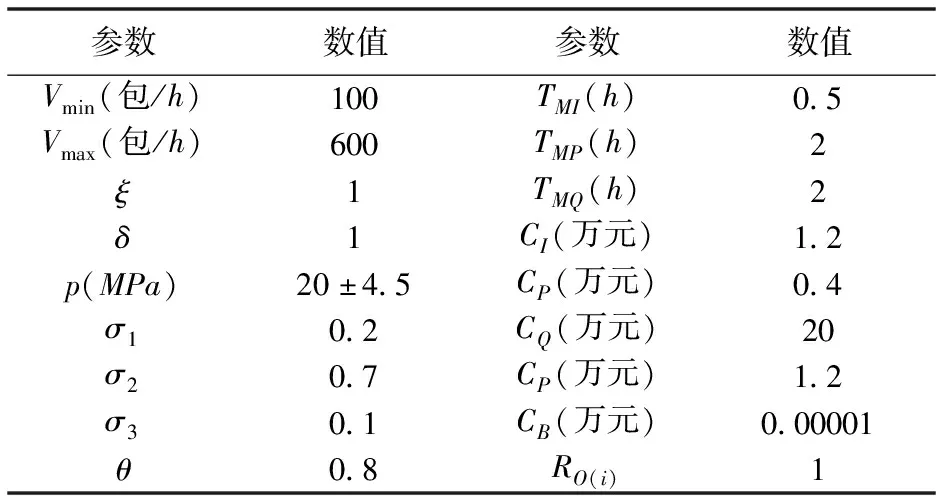
(1)生产线的运行速度v须满足:生产线的速度极限vmax大于或等于其生产线的运行速度v;此外,在客户订单量影响下,生产速度v必须要在大于vmin。综上,该运行速度v约束条件为:vmin (2)工作期和维护期组成一个订单周期,若任务结束后处于正常运行状态,则任务结束后可实施预防性维护或更换;若处维护状态,不需要再进行维护,订单周期可表示为: T订≤T=ΣTO(j)+ΣTM(j)≤T订+ΣTM(m) (21) (3)缓冲库存单元UB(i)的库存量需保证B(i)≥B(i)Min,即 (22) (4)更换活动的条件是预防性维护每次累计数为NR的整数倍时,受生产效益影响,当可靠度小于或等于可靠度阈值Rγ时执行单元进行维护,故NR满足: NR≥1,且NR为整数 (23) 在工作期后执行单元需要进行预防性维护活动或更换活动。设役龄恢复因子θi,当执行单元可靠度阈值为Rγ,执行单元UA(i)在TO(i,j)期间完成预防性维护后,可靠度改善为: R*(i,j+1)=R(θiTO(i,j)) (24) 当累计进行NR次预防性维护时,对执行单元进行一次更换,其可靠度改善效果变为: (25) 由式(1)、式(3)联立可得,各执行单元的工作期TO(i,j)为: (26) 由执行单元工作期得生产线工作期矩阵: (27) 在维护期TM(i,j)内,执行单元UA(i)在TO(j)内进行NI(i)次小修。当可靠度R(t)≤Rγ时,执行单元UA(i)需要被维护。累计进行预防性维护达到NR次时进行一次更换,则执行单元UA(i)在一个预防性维护周期T(j)内,总维护时间为:TM(i,j)=TMP(i,j)+TMI·NI(i,j)或TM(i,j)=TAQ(i,j)+TMI·NI(i,j)。 本文采用启发式算法进行仿真验证,求解思路过程如图2所示。 生产线在工作期TO(i,j)内以速度v正常运行,其可靠度随着持续运行而下降,在此期间,以周期TI(i,j)对生产线各执行单元进行NI(i,j)次小修活动,NI(i)和TI(i,j)为: (28) 以速度v正常运行的生产线,其生产线每个工作期的理论工作时间为TO(j)=minTO(i,j),则TO(j)={minTO(i,1),minTO(i,2),…,minTO(i,m)}。 维护策略可以描述为: 执行单元UA(i)维护的决策:执行单元UA(i)剩余时间ΔTO(i,j)=TO(i,j)-minTO(j)-TM是否超过下一次工作时间TO(i,j+1),且判断执行单元UA(i)累计维修次数NR能否整除NP(i)。 为了下一次的工作期TO(j+1),通过重新比较TO(j)中第j+1列数据的大小,并将得到的minTO(j)更新TO(j+1)。计算每个单元的累计维修次数NP(i),为下一次维护决策提供依据。 已知某包装企业的串行包装生产线可分为5个执行单元,其生产线相关参数如表2所示。各执行单元属性相关参数如表1所示。 表1 生产线相关参数 表2 执行单元相关参数 企业生产线实际生产中,带缓冲包装生产线的运行速度为450(包/h),缓冲库存为350(包),通过启发式算法对多目标优化模型进行仿真。假设1600h的订单周期,优化的运行速度v范围为:100~600(包/h),更换前维修次数NR的优化范围为:1~10(NR为整数),缓冲库存B优化范围为:B≥100。 对多目标优化函数G(t)进行仿真分析发现,当NR≥6时,参数NR对优化函数G(t)没有影响,故后文对优化函数G(t)的分析基于参数NR=1~6,优化曲线如图3所示。由仿真结果可知,当v=257(包/h)、B=170(包/h)、NR=3时,优化函数G(t)有最优解,此时GMin(t)=33.8106(万元)。 带缓冲生产线最优解条件下的有效运行速度为:VRζ=189.24(包/h),维护成本为:MCζ=24.0136(万元),最小缓冲库存为Bζ=170(包)。而在基于实际生产的生产线运行参数条件下,有效运行速度为:VR0=373.99(包/h),维护成本为:MC0=144.056(万元),B0=350(包)。 通过以上数据分析可得,采用本文的决策方法有效地解决了生产线平衡问题,其维护停机时间和维护成本均被降低。与企业原有的维护策略相比,本维护优化策略下,优化函数最优值条件下减少维护成本83.3%,缓冲库存降低51.4%,有效运行速度减小49.4%。基于此模型结合实际订单情况,为企业设置合理参数提升产能提供依据。 此外,本次研究对影响多目标优化函数G(t)的一些关键参数包括运行速度v、更换前维修次数NR、缓冲库存量B进行了分析,如图4~6所示。 以最优解vRO=373.99(包/h),B=350(包),NR=3为例。分析运行速度v对优化函数G(t)的影响,以缓冲库存量B为定值(B=170(包))时,由图4可知,当运行速度v=257(包/h)时优化函数G(t)具有最小值,当运行速度v增大时优化函数G(t)增长率较运行速度v减小时优化函数G(t)增长率小。分析缓冲库存量B对优化函数G(t)的影响,以运行速度v为定值即v=257(包/h)时,由图5可知,缓冲库存量B与优化函数G(t)值成正比例关系,即缓冲库存量B的增大引起G(t)值的上升。分析更换前维修次数NR对优化函数G(t)的影响,将缓冲库存单元缓冲量B和运行速度v设为定值(B=170(包)、v=257(包/h)时),由图6可知,当NR≤3时,随着NR增大,优化函数G(t)逐渐减小,当NR≥3时,随着NR的增大,优化函数G(t)的变化不大。 本文针以带缓冲多单元串行生产线为研究对象,提出了预防性维护建模与运行参数优化方法。引入役龄恢复因子、磨损模型和生产节拍,建立生产线的可靠性模型、缓冲库存模型。将生产线的工作期和维护期,有效运行速度VR、维护成本MC、缓冲库存量B基于可靠度阈值作为优化目标,并用启发式算法求解。本文案例表明,所提出的维护策略,可在保障可靠性下为生产线选定合适的运行速度和缓冲库存,提升生产效益的同时降低维护成本,为实际生产中制定串行生产线的维护决策及设定运行参数提供新方法。3.2 生产线的工作期与维护期
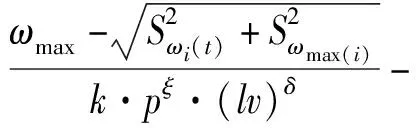
3.3 生产线的维护策略


4 实例验证

5 结论
