供应链金融信贷市场三方演化博弈动态
2022-02-16王先甲顾翠伶何奇龙赵金华
王先甲, 顾翠伶, 何奇龙, 赵金华
(1.武汉大学 经济与管理学院,湖北 武汉 430072; 2.河南工业大学 管理学院,河南 郑州 450001; 3.郑州大学 商学院,河南 郑州 450001)
0 引言
当前,大力发展经济是满足人民美好生活需求的关键。中小微企业(Medium and Micro Enterprises,下文简称MME)对经济及社会的发展有着积极的影响作用,有益于投资、创新、就业和社会发展的稳定。国家重视并大力促使MME的进一步发展,从而达到经济全面发展的目标。目前,我国的创新创业政策等实际上就是在给MME提供更多的支持与机遇。然而,在MME进行采购、生产等活动时,经常会出现流动资金有限或短缺的情况,因而需要通过各种途径进行融资,以维持企业正常的运营与发展。MME[1]不仅资金有限或短缺,同时也缺乏良好的财务制度,使得其无法提供融资的信用信息,导致大多数的MME在融资过程中都会面临风险大、成本高的难题,进而制约这些企业的发展。
供应链金融(Supply Chain Finance,下文简称SCF)的概念始于二十世纪的80年代,新世纪初得到了迅猛的发展,2007年胡跃飞[2]在描述SCF产业的发展背景时,界定了被学界广泛认可的SCF的概念。目前,国内外对SCF研究的文献已很多,我们选择中国知网与Web-Science数据库进行关键词搜索,得到关于SCF研究文献年际发文量的变化,见图1。由图1可知,虽然关于SCF研究的文献量每年都在不断地增加,但国内却只有很少部分的文献刊在核心或CSSCI源期刊上,这表明国内对SCF的研究还不深,其中大多的研究也主要集中于运营模式[3~5]、风险评估[6,7]及各参与主体之间的博弈动态[8,9]等方面。
演化博弈理论(Evolutionary game theory,下文简称EGT)[10~12]综合了经典博弈论及生物演化动力学的基本思想以揭示动物群体行为的变化特征。EGT是一种建立在参与人“有限理性”基础之上的博弈,具有有限理性的博弈参与人不会在最开始就选择最佳策略,而是通过不断地学习、调整,最终达到动态演化的稳定状态。EGT弥补了经典博弈理论的许多不足之处,被广泛应用于经济管理等学科的多个领域[6,13~15]。
目前,EGT在SCF相关问题的分析研究中也得到了不少的应用[8,9,16~20]。其中,谭喻萦和杨筝[16]研究SCF业务的委托-代理及融资决策问题,并根据对各方之间合作竞争关系的演化进而分析预期的收益。邹小红等[17]利用信贷平台与融资企业之间的博弈模型,分析网络效应对融资企业、信贷平台行为的影响作用。陆旦强[18]以两个演化博弈模型分析游离状态与不游离状态的中小企业与银行之间的博弈动态,发现核心企业(Core Enterprise,下文简称CE)与中小企业稳定的合作关系可以强化银行与中小企业间的合作,进而协助中小企业从银行获得融资。李小莉和辛玉红[8]在传统信贷与SCF信贷的两种模式下,探讨SCF业务对MME信贷的影响作用。毛晟栋和朱其特[9]在传统物流业务间加入SCF融资业务,以SCF的视角建立物流企业与中小企业间的演化动态模型,为SCF的发展提供相关的建议及决策依据。盛鑫和陈长彬[20]考虑政府的参与行为,建立物流企业与金融机构(Financial Institutions,下文简称FI)的演化动态模型,分析SCF业务系统的演化动态。
上述文献利用EGT对SCF的相关研究,从不同的角度分析了中小企业(或MME)与FI、CE之间的演化动态,但还没有将FI、CE和MME作为一个统一的系统来研究三个主体的演化博弈问题的。为弥补上述文献的不足,本文借鉴绿色供应链[21]、网络舆情[14]等问题中的三方演化博弈的研究思路,构建“FI-CE-MME”的三方参与的非对称演化博弈动态模型,探讨分析博弈模型的演化路径及演化均衡状态。本文具体内容安排为:第二部分,首先描述所研究的问题及基本的假设,然后建立FI-CE-MME间的博弈模型;第三部分探讨三方博弈动态的渐进稳定性并进行数值分析;最后是本文的结论。
1 金融机构、核心企业及中小微企业间的演化动态模型
SCF是FI将供应链上的CE及各个MME联系在一起提供金融服务的一种新融资模式。为了使自身及供应链整体的利益达到最大,CE往往选择利用自身的信用(如SCF中的融资担保等)帮助MME获取FI的贷款,并通过终止合作等方式对MME的经营行为进行约束和监督,以维持供应链系统的整体信用及长期平稳发展[22]。本文以SCF中的应收账款类融资模式(图2示)为研究对象,利用EGT构建基于“FI-CE-MME”的SCF三方演化模型(图3示),分析系统的均衡状态,进而探讨系统演化稳定性的经济意义并给出相关建议。
1.1 模型假设及参数说明
假设1以供应链上的CE、MME以及FI为博弈的三个参与者,且以三个参与者构成的信贷市场为研究对象。假设三个利益主体均为有限理性,且以自身利益最大化为决策的目的,在策略选择的过程中依据自身学习能力及博弈结果逐步调整策略。另外,由于博弈的三方在分析、判断能力等方面存在差异性,因而博弈过程中存在信息的不对称,导致博弈随机以及行为交互影响。
假设2三个博弈参与者的可选策略分别为:FI的策略集为{提供贷款(PI),不提供贷款(NPI)};CE的策略集为{担保(G),不担保(NG)};MME的策略集为{不违约(ND),违约(D)},这里违约指不偿还FI贷款本息,不违约指偿还FI贷款本息。
假设3假设FI选择为MME提供贷款策略PI的概率为x,选择不提供贷款策略NPI的概率为1-y;CE选择担保策略G的概率为y,选择不担保策略NG的概率为1-y;MME收到FI的贷款后不违约的概率为z,选择违约的概率为1-z,其中x,y,z∈[0,1],且x,y,z均是时间的函数。
假设4假设FI和MME都存在一定的机会成本。考虑到时间价值,当FI出现贷款余额时其机会成本是贷款利息,对于CE和MME而言,机会成本是指MME没有获批贷款导致供应链不能正常运营失去的利益。
假设5当CE为MME的融资贷款进行信用担保时,CE对MME的经营活动负有监督管理职责。当MME违约时,CE将给其惩罚,如占有其科技技术、将其从供应链中去除等。
假设6在CE为MME提供信用担保时,假设MME收到FI的融资贷款为m1,贷款利息为r。此时,FI对供应链及其CE实施资质调查,需要付出一定的成本,但该成本相比于直接对MME贷款进行调查评估的成本而言,可以忽略不计。若MME在收到贷款后不违约,即按期归还贷款本息,则CE的收益为R1,MME的收益为V1。若MME在获得贷款后选择违约,则本息将有CE代为归还。此时,MME获得投机收益V3,这里V3=m1(1+r)r′,其中r′为投机收益率,同时受到CE的惩罚T。此外,MME的违约将使其失去CE的信任,进而导致其失去未来预期的收益V0。未来预期的利益越高,MME越不容易选择违约,反之,越容易选择违约。
假设7在CE不为MME提供信用担保时,FI若要给MME提供贷款款,必须要对MME的资产、信誉等进行审核评估,设评估成本为C。在评估合格后,MME获得的贷款金额记为m2(m2 假设8在MME无法获得FI的融资贷款时,MME与CE都将因资金短缺受到负面影响。 表1 主要参数设定及含义 根据问题的描述及2.1节的模型假设,我们可以得到SCF信贷市场三方博弈的收益矩阵,见表2。 表2 三方博弈的收益矩阵 1.3.1 金融机构选择提供贷款策略的复制动态方程 首先,假设FI提供、不提供贷款时的期望收益为πx1和πx2,根据表2中的博弈收益,有: πx1=ym1r+(2zr-1-r+z)(1-y)m2-(1-y)C (1) πx2=-ym1r-(1-y)m2r (2) FI选择提供、不提供贷款策略时的收益差记为: πx1-πx2=y[2rm1-(2zr-1+z)m2+C]+ (2zr-1+z)m2-C (3) 因此,FI选择提供贷款策略PI的复制动态方程为: =x(1-x){y[2m1r-(2zr-1+z)m2+C]+ (z-1+2zr)m2-C} (4) (z-1+2zr)m2-C} (5) 此时分两种情况来讨论: 1.3.2 核心企业选择担保策略的复制动态方程 假设CE选择为MME提供、不提供担保策略的期望收益为πy1和πy2,根据表2的博弈收益,有: πy1=x[2R1-(1-z)(r+1)m1+(1-z)T1]-R1 (6) πy2=(2x-1)R2 (7) CE选择提供、不提供担保策略的收益差为: πy1-πy2=(2x-1)R1-x(1-z)m1(r+1)+ x(1-z)T1-(2X-1)R2 (8) 因此,CE选择担保策略G的复制动态方程: =y(1-y){x[2(R1-R2)-(1-z)· (r+1)m1+(1-z)T]-(R1-R2)} (9) m1(r+1)+x(1-z)T1-(2x-1)R2] (10) 此时分两种情况来讨论 1.3.3 中小微企业选择不违约策略的复制动态方程 假设MME选择不违约、违约的期望收益分别为πz1和πz2,根据表2中的博弈收益,有: πz1=x(r+1)[ym1+(1-y)m2]+ (2x-1)yV1+(2x-1)(1-y)V2 (11) πz2=(2x-1)y(V1+V3)-xy(T+V0)+ (2x-1)(1-y)(V2+V4) (12) MME选择不违约、违约策略的收益差为: πz1-πz2=[ym1+(1-y)m2]-2xyV1-(2x-1)yV3+ xy(T1+V0)-(2x-1)(1-y)V4 (13) 因此,可得MME选择不违约策略ND的复制动态方程为: =z(1-z){-x(r+1)[ym1+(1-y)m2]- (2x-1)yV3+xy(T+V0)-(2x-1)(1-y)V4} (14) (2x-1)yV3+xy(T+V0)-(2x-1)(1-y)V4} (15) 此时分两种情况讨论: 由上述分析,我们可以给出三个利益参与主体的博弈动态模型为: (16) 令F1(x)=0,F2(y)=0及F3(z)=0,可以得到演化博弈动态过程的均衡点。在非对称博弈中,若博弈演化的均衡是演化稳定策略,则其一定是严格纳什均衡,而严格纳什均衡又是纯策略均衡。也就是说,非对称博弈动态中混合策略均衡一定不是演化稳定均衡[14,23]。因此,对于由SCF上的三方参与主体构成的信贷系统而言,只讨论纯策略E1=(0,0,0),E2=(0,0,1),E3=(0,1,0),E4=(0,1,1),E5=(1,0,0),E6=(1,0,1),E7=(1,1,0),E8=(1,1,1)的渐进演化稳定性。首先,当博弈动态模型(16)的Jacobi矩阵的所有特征值λ<0时,该点为渐进稳定点;当Jacobi矩阵所有的特征值λ>0时,该点为不稳定点;当Jacobi矩阵的特征值λ有正有负时,该均衡点是不稳定的,即鞍点。 将F1(x),F2(y),F3(z)分别对x,y,z求一阶偏导,即得式(16)的Jacobi矩阵: (17) 其中 =(1-2x)[y[2m1r-(2zr-1+z)m2+C]+ (z-1+2zr)m2-C] (18) =y(1-y)[2(R1-R2)-(1-z)(r+1)m1+(1-z)T] =(1-2y){x[2(R1-R2)+(1-z)T- (1-z)(r+1)m1]-(R1-R2)} (19) =z(1-z){-(r+1)[ym1+(1-y)m2]- 2yV3+y(T+V0)-2(1-y)V4} =z(1-z){-x(r+1)(m1-m2)- (2x-1)V3+x(T+V0)+(2x-1)V4} (20) =(1-2z){-x(r+1)[ym1+(1-y)m2]+ xy(T+V0)-(2x-1)V4+(2x-1)y(V4-V3)} 根据Jacobi矩阵所有特征值的符号来判断演化均衡点的稳定性,结果见表3示。 表3 均衡点的稳定性分析 定理1当V0-V3<(r+1)m1-T 定理1中结论的相位图见图4与图5。由定理1可知,当未来预期的收益较小时,MME将倾向于违约。反之,当未来预期收益越大时,MME将选择偿还FI本息,以获得CE的信任从而保证预期的收益,因此越不容易违约。由此可以推断,如果地方政府或国家政策对MME的融资给予降息或是补贴优惠,将有助于增强MME的收益信心,进而提高MME的未来收益,从而促使系统趋于渐进演化稳定点E8(1,1,1)。此外,CE在对MME进行担保的同时,也对其经营等各种经济行为进行监管。MME在违约时受到的罚金越大,其成本也越大,因此越不容易违约。李小莉和辛玉红[8]也已证明,在获得贷款后若MME的违约成本较小,则很可能选择出现违约行为。在CE提供担保时,MME的违约将受到惩罚,也将失去供应链的预期收益,因此违约成本增大,从而选择不违约。若MME选择违约,将会给CE带来连带的责任,进而将影响供应链各企业的信用与效益,一定程度上阻碍了供应链整体业务的合作发展,因而应尽力避免和杜绝此类事件的发生。 为更直观分析供应链信贷系统的演化动态,对博弈动态模型(16)做数值分析。基于假设(r+1)m1+V3 在上述给定条件下,以初始值x0=0.3为例,随机选取和的初始值,x值随时间的变化见图6。由图6可知,y和z初始值的不同会对x的收敛速度产生影响,但x均单调递增并收敛于1,这说明FI选择贷款策略的概率随着时间持续增加,且系统最终演化到所有FI都选择贷款策略的稳态。图7给出初始值y0=0.5时x,z初始值的变化对y值演化动态趋势的影响,CE提供担保的概率y随x,z初始值的变化而不同,但系统最终演化到所有CE都选择担保策略的稳态。图8给出初始值z0=0.3时x,y初始值的变化对z值演化动态趋势的影响,MME不违约的概率z随x,y初始值的变化而变化,但系统最终演化到所有MME提供信用担保的稳态。此外,同样在上述条件下,我们给出FI、CE和MME三个博弈主体的策略演化路径,见图9。由图9可知,对于x,y,z的不同初始值x0,y0,z0,系统最终都演化至x=1,y=1,z=1的理想均衡状态E8(1,1,1),这与理论求解的结果一致。 MME对国家经济的发展起着举足轻重的作用,但其融资中的各种难问题又是不可避免的。SCF以供应链上CE的信用资质作为担保,转变了FI对企业信用的审核方式,从而降低了MME进行融资贷款的门槛,为其提供一种新的融资贷款方式。本文基于FI、CE及MME构建三方利益者间的演化动态模型。根据对动态模型的分析可知,SCF信贷系统的演化趋于FI选择为MME提供贷款、CE选择为MME提供担保、MME选择不违约的稳定状态。对MME而言,其预期获得的利润越高,越倾向于选择不违约策略ND;此外当其投机收益变小、使得违约成本相应变大时,也越倾向于选择不违约。因此应提高MME的预期收益,促使系统向着动态均衡E8(1,1,1)的方向演化。基于本文的研究我们给出以下几个建议:(1)中央政府和地方政府应鼓励社会资本设立专项基金,为SCF提供融资业务的支持;同时也可以通过降低贷款利息、或者给予MME贷款补贴,扶持MME,进而保证整个供应链系统正常有效的运作。(2)强化SCF监管环境。利用互联网构建相关公共服务平台,实现利益主体的信息共享,借助信息共享平台,加强FI、公众等对MME经济经营的监督。(3)提高对SCF业务活动的监管、提高风险管理水平,从而减少MME融资后投机的概率。
1.2 收益矩阵

1.3 复制动态方程
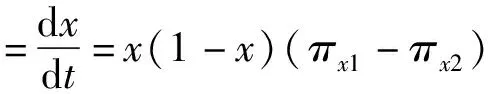


2 演化稳定性分析
2.1 均衡点及渐进稳定性分析
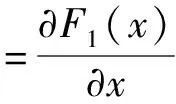




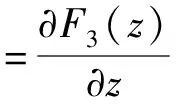

2.2 演化稳定策略分析
2.3 数值分析
3 结论
