证据独立性及其对目标识别的影响研究

关 欣, 于昊天, 衣 晓

(海军航空大学, 山东 烟台 264001)

0 引 言

置信函数来源于“lower probabilities”,在20世纪60年代由Dempster提出。到了70年代,Shafer将其引申发展为证据理论,因此证据理论又被称为Dempster-Shafer证据理论(简称为DST)。证据理论用基本概率赋值(basic probability assignment,BPA)函数表征某个命题的信任度。DSmT(Dezert-Smarandache theory of plausible and paradoxical reasoning)克服了DST内在的限制,展现出很大的优势。

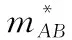
然而,从Smets定义出发,发现Dempster组合规则似乎违反或破坏了证据的独立性,而DSmT理论并未出现这样的问题。

当前判断证据的独立性没有统一的方法,其中一种方法是基于概率统计中的相关系数来判断独立性。这种方法对于大样本情形是有效的,但概率论中常用的相关系数本质上是研究随机变量间线性关系的函数,并不能涵盖所有的相关关系。小样本或无样本情形使得这种方法的可靠性大大降低。本文将从Smets定义出发,针对小样本或无样本情形,从目标信息独立性的角度,提出一种解释和判断独立性的方法。

证据独立性是Dempster和DSm证据组合规则的前提,然而真实世界的信息之间往往存在着不同程度的相关性。如果忽略证据之间的相关性,或者说默认证据之间的独立性,直接使用Dempster等组合规则将导致不合理的结果。本文将对Zadeh悖论进行讨论,给出新的分析和解释。

为了解除独立性对Dempster组合规则的限制,也就是研究相关证据组合问题,目前主要有两种方法。一种方法是对证据源进行处理从而消除相关性,这种方法认为相关性是由于同一证据源与两个证据源合成产生的,而这种假设的局限性在于假设共同信息是以共同证据源的形式存在的。另一种方法是对Dempster组合规则进行修改而消除独立性的限制,来解决相关证据的组合问题。这类方法使用的前提是对于不同证据体的信息共享部分有一定的先验知识,则可以针对相关部分进行处理,从而消除相关的影响。对于具有高冲突特性的证据组合问题,其处理也暗含了一定的先验知识。

如何对没有上述前提的相关证据进行组合呢？由于证据理论是概率论在一定意义上的推广,因此类比概率论,可以把证据的独立性关系分为完全独立、完全相关和混合相关。一定条件下,混合相关情形的概率组合介于独立和完全相关情形的概率组合结果之间,那证据是不是也有类似结论呢？

综上,由于目前没有关于证据独立性判断的统一方法,而且基于大样本情形的相关系数判断法方法对于小样本或无样本情形不适用。因此,针对小样本或无样本情形,本文尝试从逻辑的角度出发探讨独立性判断问题。基于Smets关于证据独立性的定义,研究提出一种基于目标信息独立性的证据独立性判断方法。通过对证据独立性的分析,不仅可以对经典的Zadeh悖论从新的角度进行讨论,也可以为目标识别中不同传感器独立性的合理判断提供指导。最后,基于目标识别背景,针对小样本的相关证据组合问题,考虑从复合事件概率组合中借鉴方法,探索合适的组合方法。

1 证据理论

1.1 BPA

设={,,…,}是一个元素有限的识别框架。

在DST中,元素是完备和互斥的。2表示的幂集,记为2=(,∪)。定义BPA函数:2→[0,1]满足

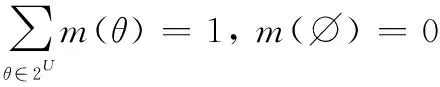
(1)

在DSmT中,元素可以相交。令表示的超幂集,记为=(,∪,∩)。其BPA函数满足

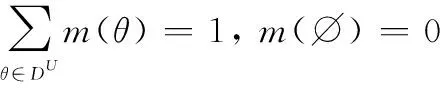
(2)

1.2 经典组合规则

121 Dempster组合规则

Dempster组合规则来源于DST中的Shafer模型。假设识别框架定义在={,,…,}上的两个独立的等可靠的BPA：和,则和的Dempster组合规则满足:

(1)(∅)=0;

(2) ∀(≠∅)∈2,有≠时：

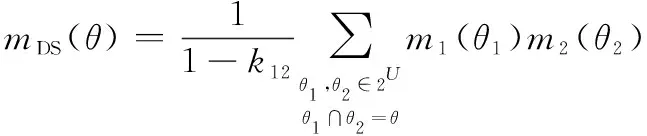
(3)

其中,表示冲突度：

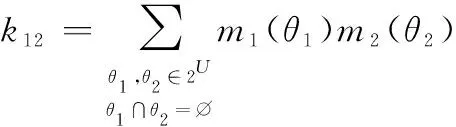
的使用前提是当且仅当式(3)的分母非零,即<1。

122 经典DSm组合规则

假设同一识别框架下两条独立、不确定、高冲突的信源、,以及定义在上的两个广义BPA函数、,经典DSm组合规则定义为对∀∈-{∅}。有:

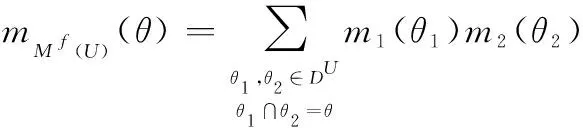
(4)

式中：()(∅)=0,除非在特殊的例子中信源把非零值赋给空集(如Smets的概率转换模型)。

2 证据独立性判断方法

1976年Glenn在《A mathematical theory of evidence》书中提出信度函数的组合基于证据体的独立性,这一组合的前提条件被很多组合规则采纳。例如,DSmT遵从了Smets对证据独立性的定义。

2.1 Smets对证据独立性的定义

在文献[5,29]中,Smets如下定义了证据体的独立性。

(1) 如果一个信度函数满足:除了全集以外,所有真子集的信度值均为0,那么这种信度函数称为空信度函数。

(2) 证据体对应的限定于空间中的一个区域。对于空间和。给定证据体1表示的一个子集为真,证据体2表示的子集为真,在某个新的空间上构造信度函数Bel和Bel。考虑由证据体1(为真)诱导出的上的信度函数Bel(·|),以及由证据体2(为真)诱导出的上的信度函数Bel(·|)。如果两个信度函数都是空信度函数,那么就称这两个证据体是独立的。因此,两个证据体独立的条件是:其中一个证据体对另一个证据体的信度值完全不知道。

基于上述定义回顾Dezert给出的例子。

一个75岁的老人和他9岁的孙子看到了一个45岁左右的抢劫犯正在抢夺一个老妇人的包。警察向他们询问抢劫犯的信息(年龄大还是小)。基于识别框架={=年轻,=年老},利用DSm模型将证词记为

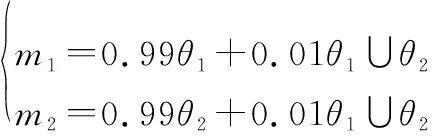
这两个证据体存在高冲突性。利用DSmT组合规则,得到新的BPA：

=0009 9+0009 9+
0000 1∪+0980 1∩

因此,结论是∩,即警察确认抢劫犯比老人年龄小且比孙子年龄大。

如果令和分别代表由老人和孙子提供的证据所对应的概率空间。基于老人的认知,的子集和分别对应年轻和年老。同样,基于孙子的认知,的子集和分别对应年轻和年老。

现在,假设警察还对其证词一无所知。显然,在空间和上的置信度分布函数都是空置信函数。假设是真,即抢劫犯相对于老人是年老。一般来说,抢劫犯相对孙子也应该是年老,这就是说是真的可能性也很大,同时是真的可能性很小。换句话说,基于“是真”条件下,上的置信度函数不是空置信函数。同样的方法,基于“是真”条件下,上的置信度函数也不是空置信函数。所以,由老人和孙子提供的证据体是非独立的。

2.2 Dempster组合规则中的独立性问题

对于识别框架的两个证据和,,,… 和,,… 分别是两个证据的焦元。用表示合成之后的证据。对于Dempster组合规则,如果∩=∅,则认为,是矛盾的,∩不可能发生,即(|)=0。

于是,对于证据上的信度函数Bel,有Bel(|)=0且Bel(-|)=1。因此,按照Smets对独立性的定义,由(为真)诱导出的上的信度函数Bel(·|)一定不是空函数,即与不是独立的。基于此,Dempster组合规则中,把∩=∅当做矛盾处理与证据独立性这个条件是背离的。而对于DSm理论模型,允许组合后∩的存在,就不会出现这样的问题。

事实上,仅从组合的计算形式上来看,两个独立证据源所涉及的事件之间不存在矛盾,但是实际中,某些事件组合不可能发生,因此人为将其归为空集(如∩=∅),这实际上是引入了新的信息,或加入了限制。换句话说,在加入这种特定限制之前,证据是严格独立的,这种限制的引入在一定程度上破坏了独立性,引入了相关性。从这个角度来讲,对于利用冲突再分配策略的组合方法,都不是严格意义上的基于独立性的组合方法。或者说,冲突再分配策略处理的证据组合问题,证据之间不是严格独立的。

2.3 证据组合的内涵

在目标识别中,通过观察和测量手段获取目标的特征信息,经过信息处理,得到一个目标的像或模型,这个像包含了对目标的所有认知信息。对于多源信息融合系统,需要对多个信源的信息进行融合,每个信源都提供了目标的一部分或全部信息,为得到目标最终的像提供依据。

从证据理论的角度来看,每个信源提供的证据都代表了一种目标的像,包含了目标的一部分或全部信息。证据组合的过程就是对这些信息重新整合，从而建立一个新的像。所以,证据组合的内涵就是对证据所提供信息进行组合,组合的对象是目标信息而非信源。图1和图2分别是证据组合的外在表现和内涵示意图。

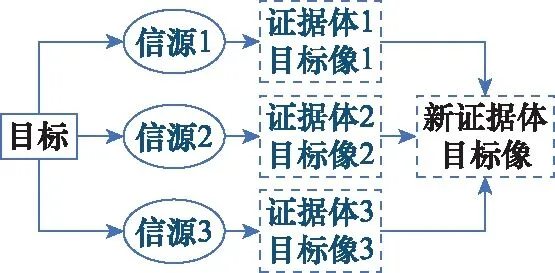
图1 证据组合的外在表现Fig.1 Outward expression of combining evidence

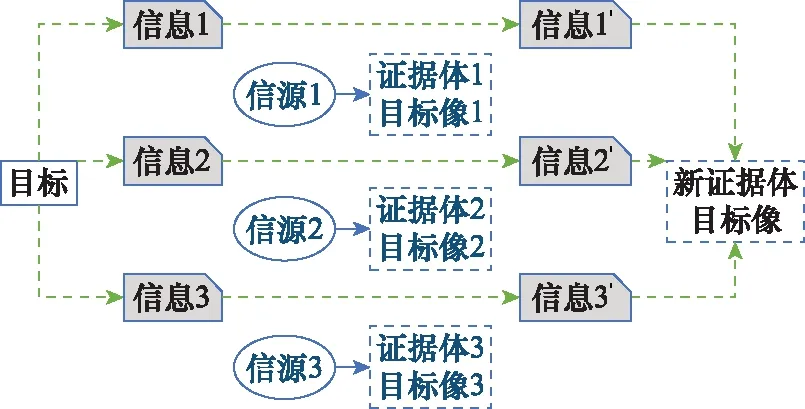
图2 证据组合的内涵Fig.2 Connotation of combining evidence

实际问题中,多个证据可以基于同一个识别框架,但是这些证据隐含的意义是不同的。如例1所述,老人和孙子对同一识别框架的认识是有差别的,因为其判断标准不同。但是其所提供的证据仍然不是独立的,那是因为都是基于目标的同一属性(即抢劫犯的年龄)做出的判断。所以说,真正影响独立性的不是判断标准是否一致,而是目标的属性是否一致。一般来讲,在对一个目标做出判断的时候,依据的是目标的某些属性(特征)。例如,中国寓言故事《盲人摸象》中,盲人们分别给出大象是萝卜、簸箕、石头、木臼等结论,实际解释则是大象在牙齿、耳朵、头、腿这些属性上与上述这些描述是一致的。

因此,如果目标有多个属性,而信源基于目标属性进行目标识别,那么证据体对识别框架的解释是:目标的某个或几个属性与识别框架中的元素具有一致性,BPA的大小则反映了一致性的相对程度。

考虑一个多传感器数据融合的例子。设表示战斗机,表示多用途或地面攻击飞机,表示轰炸机,目标识别框架={,,}。传感器系统使用电子支援措施、红外、光学成像3种传感器,提供的证据分别为、和。

那么()=02表示目标在射频(radio frequency,RF)频率、脉冲宽度(pulse width,PW)这两个属性上,与战斗机的一致性程度是02;()=()=03则表示目标分别在波长和光学设备这两个属性上,与战斗机的一致性程度都是03。虽然()=(),但是其对识别框架的解释完全不一样。

因此,在应用证据理论进行信息融合之前,需要对不同证据包含的意义做出准确的分析。这一点,在关于Zadeh悖论讨论还会有涉及。

2.4 一种独立性的逻辑判断方法

证据组合的内涵是对证据所蕴含目标的信息进行组合,因此可以依据是否包含目标共同的信息来判断独立性,即包含共同信息的证据一定是相关的。反之,独立性的证据不包含共同信息。文献[15-18]则依据共有知识判断相关性。

实际应用中如何判断是否包含共同信息,可以从信息特征或目标属性的角度来分析。关于独立性的判断,这里提出两个判断准则。

(1) 证据体独立性的判断应当依据不同信源所掌握目标信息的独立性而不是信源的独立性。信息源于目标,信源是信息的渠道或载体。信源的独立性说明了获取信息途径的方法或过程是独立的,但是对于信息是否独立没有决定性作用。一方面,不同信源可以对目标的同一信息给出结论。例如,对于一个人身高的判断,可以从不同角度(正面、侧面、背面)判断,可以从不同媒介(照片、视频)判断,甚至可以通过影子的长度来判断,但是不同方法最终聚焦在身高这个特征信息上。再来看“指认抢劫犯的例子”,老人和孙子虽然可以独立给出证词,但都是关于年龄这同一信息的判断。另一方面,同一信源可以对目标的不同信息给出结论。例如,对一个人的声音和身形两个方面的信息,可以同时获得,也可以只获得其中一个。所以,依靠信源的独立性来判断证据的独立性是值得商榷的。同时,由于不同信源的可靠性不同,或多或少都存在误差,所以不同信源对同一信息得到的结果也是有差别的。

关于信息独立性的判断和衡量可以借鉴概率论中事件独立性判断方法。数据分析可以作为一种方法,但在缺乏数据或小样本的情形下,则需要通过逻辑上的判断。

(2) 对于具有独立属性的目标,由该目标不同属性产生的信息是独立的,基于这些独立信息的证据也是独立的。但是同一个目标的不同属性不一定是独立的,这些属性间也可以存在联系。例如,水果的味道和外观是两个属性,但是一般情况下,味道和外观都能独立的作为判断水果种类的依据,所以这两个属性之间的相关性很强。由于真实世界中,事物的联系是普遍存在的,因此只能在一定误差范围内对独立性做一个大致的判断。

这种判断方法是满足Smets定义的。事实上,设目标包含可列个独立属性{,,…},对任意属性(=1,2,…)存在状态集合(),选定状态集合：

={(,,…)|()∈(),=1,2,…}

取、为两个不同属性的状态集合()、(),那么对于任意⊆()和⊆(),其选取互相没有影响,因此上的信度函数Bel(·|),以及上的信度函数Bel(·|)也一定都是空信度函数。

对于空中目标识别来说,多个传感器得到的信息既可以是动态数据,也可以是身份信息。动态信息描述目标运动的动态参数,通常包括位置、速度和加速度。身份信息则是有助于确立目标身份的命题或陈述,目标身份信息包括传感器信号、属性信息、身份说明等。

在没有其他信息的情况下,动态信息与身份信息可以看作是不同属性的信息,基于这些独立信息的证据是独立的。例2中,3个传感器分别依据RF、PW、波长以及光学特征对目标进行判断,因此其是独立的。

但是对于都是测量位置信息的传感器,如红外传感器和激光传感器,虽然其输出数据有角度、高度或者坐标等不同形式,但是对目标非独立属性进行的识别,所以作为证据源,应该是非独立的或者完全相关的。但是,由于测量存在系统误差和随机误差,不同传感器测量的误差一般被认为是独立的。事实上,两者并不矛盾,从测量属性的角度来讲是关于同一属性的测量,在证据组合时应选用相关的方法融合;而测量结果的误差是独立的,对误差分析需要用独立性的方法来处理。

2.5 Zadeh悖论

基于本文判断方法,回顾一下著名的Zadeh悖论。1982年,Zadeh提出了下面的例子来说明Dempster规则会产生不合常理的结论。

两位医生A和B对同一个病人做检查,都认为病人可能患的疾病为脑膜炎(meningitis,M)、脑震荡(concussion,C)或脑瘤(brain tumor,T)。因此，识别框架可以记为={,,}。两位医生对疾病的判断用BPA形式表述就是：

=099·+0·+001·

和

=0·+099·+001·

当使用Dempster规则组合和时,有：

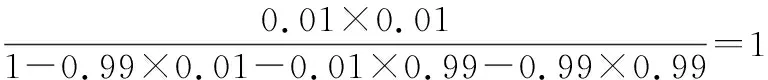
这就意味着病人患有的疾病确定是脑瘤。而两位医生都认为病人患脑瘤的可能性很小,只有001,这就产生了巨大的矛盾。Dempster组合规则在高冲突情形下会产生不合理的结论,这为该方法招致了很多批评。

很多文献对该例子进行了分析讨论,这里采用一种新的思路。

第一种情形:如果医生们的检测方法大致相同,或者其检测的是患者同一类身体指标,那么,依据判断方法,这两个医生给出的证据是相关而不是独立的。因此,不应该使用Dempster规则进行证据组合。而此时,两位医生给出的证据之间的巨大冲突主要来自于检测结果的巨大误差。

如果两个医生的检测都是可信的,就是说在误差允许范围内,两名医生对患者患病概率的估计是可信的,即患者患病的真实概率分配={(),(),()}满足：

∈(Bel,)∩(Bel,)

(5)

其中,

Bel={Bel(),Bel(),Bel()}

和

Bel={Bel(),Bel(),Bel()}

分别是由、两个医生分别给出的信度函数;、分别表示两个医生的判断误差,而(,)表示在空间中以为中心为半径的邻域。

于是,两个医生给出的证据间冲突主要来源于判断误差、。根据本例的数据,实际冲突很大,说明两个误差中至少有一个很大。因此,如果两个医生的可信度是一致的,那么比较合理的结论是：

Bel(),Bel()∈[0,099]

Bel()=001

这是因为在没有额外信息的情况下,无法判断哪个医生的判断更准确,对Bel(),Bel()给出了较为宽泛的区间估计,区间较长是由大冲突引起的,但是可以确定Bel()依然很小,这与实际是相符的。

第二种情形:如果医生们的检测方法是完全不同的,或者说医生是对患者不同的(相对独立的)身体指标进行检测,那么此时的证据是独立的。当然,两个证据的意义是不同的。假设病人具有两种完全独立的病征和(正如球的大小和颜色是球的两个完全独立的特征)。医生针对病人出现的病征进行检测,得到结果显示,病征与脑震荡完全不一样,而病征与脑膜炎和脑瘤相似的程度分别为099和001。(这一相似程度来源于:具有病征的病人中,脑膜炎和脑瘤患者人数的比例)。也就是说医生排除了脑震荡。同样的,医生基于病征给出了判断。在这一假设下,脑膜炎和脑震荡分别被病征和所排除,那么唯一的可能性就是脑瘤。在这种情形下,结论与直观认识还是一致的。事实上,病人去医院检查身体,会被要求做各种不同的检查,例如血液检查、超声波、射线检查等。这些检查很大程度上是独立的,由其所得到的结论(证据)在很大程度上也是独立的,因此可以使用Dempster规则进行组合。

3 证据独立性对目标识别的影响

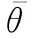
假设一个未知目标有3个属性、、,并且依据第(=1,2,3)个属性,该目标与已知目标匹配的概率为。传感器能够识别到目标、属性的信息,给出目标为的概率为;传感器能够识别到目标、属性的信息,给出目标为的概率为。表示综合3个属性未知目标为的概率。

假设传感器、识别结果如表1所示。

表1 传感器A和B对目标的概率识别结果Table 1 Probabilistic recognition results of sensors A and B on targets

从传感器、的识别信息可以发现,两个传感器可以是独立、混合相关或完全相关的。

3.1 置信度以概率方式给出

假设对某一空中目标的识别采用“与”匹配方式,即当目标的所有属性均与匹配,才能推断未知目标是。事实上,大部分目标识别的组合都属于“与”匹配,如例2,只有RF、PW、红外波长和光学设备属性都匹配时,才作出识别判断。

从识别概率角度来说,有=,=,=。

一方面,结合≤1,可知=≥。同理，=≥。于是≥max{,}。进一步有:

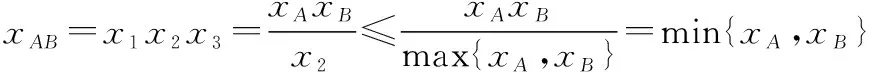
且当=max{,}时,等号可以成立。

另一方面,由于≤1,所以==≥。且当=1时,等号可以成立。

综上,得到∈[,min{,}]。基于此,有以下分析。

(1) 由于传感器没有考虑属性的影响,所以给出的目标概率中混入了不符合的情形,从而整体概率会变小。同理,整体识别概率要比传感器给出的概率也要小。

(2) 如果属性不对识别结果产生影响,此时可把属性去掉,得到表2。

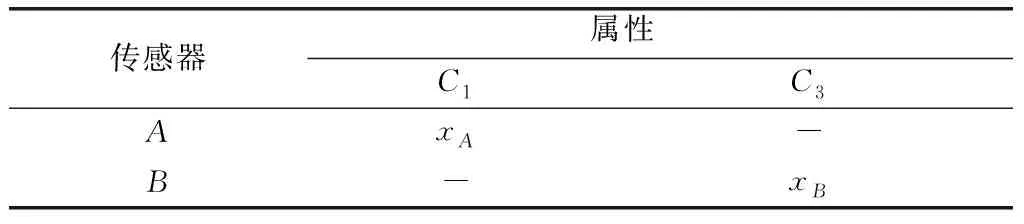
表2 传感器独立的情形Table 2 Sensor independent case

此时,、是完全独立的情形。可以利用独立事件概率计算方法,得到整体识别概率为,这也正好等于的下界。

(3) 如果属性、不对识别结果产生影响,即两个传感器都是针对属性给出的识别结果,那么其是完全相关的。由于识别环境不同,识别结果差距主要来源于识别误差。在两个传感器的可靠性一致的情况下,既可以采取平均的方法消除误差(即=(+)2),也可以对做区间估计(即∈[min{,},max{,}])。

(4) 需要说明的是,混合相关的上界是由=1推导得到的,此时就是完全相关情形。考虑到传感器的探测误差,采取了平均方法,这对于混合相关情形也是适用的。因此,混合相关情形的上界也可以写成(+)2的形式。

综上,讨论了独立、相关、混合相关情形下的整体概率的估计,识别概率与相关性关系如表3所示。特别地,无论哪种匹配方式,混合相关的组合概率均处于独立情形与相关情形之间。

表3 识别概率与相关性Table 3 Recognition probability and correlation

由于=,且∈[max{,},1],与成反比例,因此:① 当=1时,、完全独立,越大说明属性对整体识别概率的影响越小,则独立性越强;② 当=max{,}时,两者相关,且越小,相关性越强;③ 独立性越强,整体概率越接近独立情形,相关性越强,整体概率越接近相关情形。

3.2 置信度以证据形式给出

前文是置信度以概率形式给出情况,现在分析识别置信度是以证据形式给出的情形。设传感器、给出的证据:

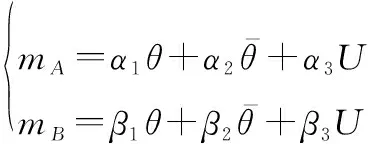
(6)

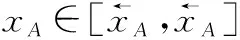
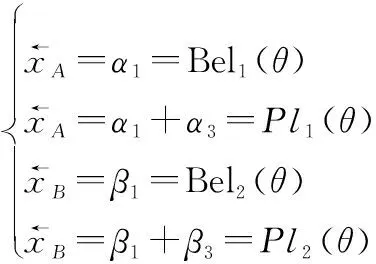
(7)

首先,分别计算上下界。一方面,由于:

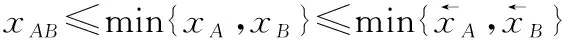
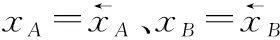
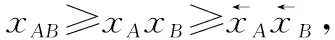
综上,可得

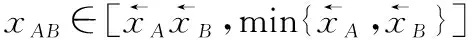
(8)

类似第31节的讨论,的上界是在传感器没有误差的情况下得到的。而此时正是在=1也就是完全相关情形,因此在没有其他信息的情况下,为了消除误差,较好的方法是用平均方法计算上界,即

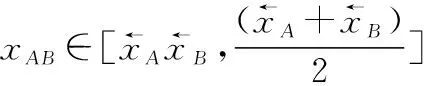
(9)

进一步将式(7)代入式(9)得

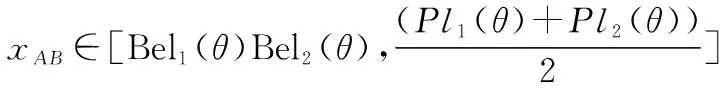
(10)

通过式(10),置信度以证据形式给出的情形下,混合相关情形识别概率也是介于独立情形和完全相关情形之间。而证据的相关性程度决定了组合结果更接近哪种情形。

于是,如果令和分别表示独立性和相关性情形的证据组合结果,则混合相关情形的组合结果结果介于前两者之间,即

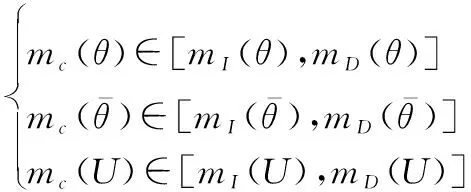
(11)

3.3 算例分析

例4 传感器、识别结果如表4所示。

表4 传感器A和B对目标的BPA识别结果Table 4 BPA recognition results of sensors A and B on targets

识别结果是以证据体BPA给出的,通过计算信任函数和似然函数得到两个传感器的置信区间∈[06,08]、∈[065,09]。按照上文所述方法得到整体概率满足∈[039,085]。

通过Dempster、DSmT以及平均组合方法可以得到:

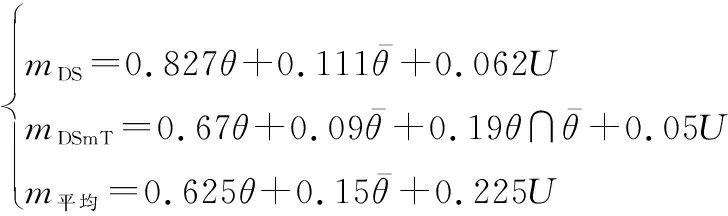
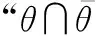
4 结 论

证据体之间相关性的不同,适用的组合方法也不同,需要依据相关性选用合适的方法进行组合。本文主要做了以下工作。

(1) 从Smets在1986年给出证据独立性定义出发,研究了证据组合的内涵、证据对识别框架的解释以及证据组合中的独立性问题。认为证据的独立性来源于证据源获取的目标信息而不是证据源,并从证据源信息属性的角度提出了一种判断证据独立性的方法,即对于具有独立属性的目标,由该目标不同属性产生的信息是独立的,基于这些独立信息的证据也是独立的。基于该方法,从新的角度研究了经典的Zadeh悖论,给出了新的分析和结论。

(2) 多传感器单目标识别为背景,研究了传感器独立性、相关性对识别置信度的影响。分别对置信度以概率形式和证据形式给出的情形进行研究,发现混合相关传感器的组合结果应介于独立传感器和完全相关传感器的组合结果之间。在没有额外信息的情况下,给出了识别置信区间。