基于深度学习的捷变相参雷达1-Bit块稀疏重构

付 蓉, 黄天耀, 刘一民

(清华大学电子工程系, 北京 100084)

0 引 言

为了应对日益复杂的电磁环境,提高目标信息获取能力,现代雷达呈现出两大发展趋势,即由低分辨向高分辨、由简单波形向复杂波形发展。捷变相参雷达是一种合成带宽体制雷达,其发射脉冲的载频可以在雷达系统的整个带宽范围内快速变化,具有宽带高分辨的特点,可以提供目标更加丰富的信息特征,同时,因其可以不断改变发射频率,故可以对干扰方侦察机进行频率欺骗,更不容易被侦察,抗干扰能力更强。

随着雷达技术的不断发展,数据量急剧增加,现有系统难以应对大容量的数据传输、存储等问题。如何有效压缩和恢复信号是信号处理领域亟待解决的问题。压缩感知理论提供了一种解决问题的有效方法,信号的采样和压缩同时进行,打破了传统奈奎斯特抽样定理的限制,少量的采样数据就可以得到很高的概率重构高维稀疏信号,因而在雷达通信等信号处理领域内中得到了广泛应用。比如,捷变相参雷达在同一个粗分辨单元内,观测到的目标个数往往较少,其分布具有稀疏性,因此相比传统的匹配滤波方法,压缩感知算法通过挖掘捷变相参雷达观测场景的稀疏性这一先验信息,可以有效抑制旁瓣、准确重建场景。

传统的压缩感知理论考虑的测量值是连续值,具有无限比特精度,然而在实际应用中,由于数据存储或传输需求,还须考虑测量值的量化问题,即在稀疏采样的同时对测量值进行量化,特殊地,1 Bit量化时测量值仅为正、负两个状态,与大量现有数字信号传输系统能很好地兼容。首先是选择合适的量化器比如Lloyd-Max量化器,根据其量化边界值与量化代表值对原始观测信号进行量化,通过信道传输至远端,最后在远端利用稀疏先验进行恢复和估计,一般转化为求最小范数的优化问题,其算法性能的理论分析有很多,常见方法有迭代阈值算法、匹配追踪算法、限制步长收敛算法、线性规划等,其中1 Bit压缩感知重构效果最佳的二进制迭代硬阈值(binary iterative hard thresholding,BIHT)算法,具有较高的重构信噪比和一致性。

但是信号重构算法运算量往往较大,难以满足雷达在对抗过程中的高数据率、高实时性的要求。深度学习的快速兴起,为高效求解上述稀疏优化问题提供了新思路。近年来,不少学者提出用深度学习网络对传统算法的迭代过程进行展开,每一步迭代对应一层参数未知的计算网络,利用多层神经网络替代原有的多次迭代,并通过大量数据学习上述网络中的最优参数,从而在有限的网络深度(即迭代次数)下对目标参数进行高质量恢复。

另一方面,由于采用合成带宽较大的捷变相参雷达进行目标探测,对于尺寸较大的目标(如民航客机、海面舰船等)将发生距离扩展现象。关于块稀疏重构问题的有效性有很多相关研究,其中,针对捷变相参雷达观测场景下块稀疏重构性能也有相应的理论分析。基于以上研究,先采用1 Bit压缩感知技术,通过挖掘雷达目标的块稀疏特性,将目标回波建模为欠定方程,并利用重建准确度高的BIHT进行求解,实现对观测目标参数的精确重建。然后,进一步将深度学习用于捷变相参雷达,对传统的迭代过程进行加速,同时将块稀疏的结构特征融入到网络结构中,实现高效快速的1 Bit块稀疏重建网络。该重建网络较之传统1 Bit硬判决迭代算法,使得雷达目标参数的恢复效果更好,并具有更快的收敛速度,最后,通过仿真实验验证了网络的恢复能力和算法的有效性。

1 基于1-Bit块稀疏恢复的捷变相参雷达目标重构

1.1 捷变相参雷达信号模型

首先介绍捷变相参雷达回波信号模型。假设雷达在一个相参处理间隔内发射个单载方波脉冲信号,第个雷达脉冲可以表达如下:

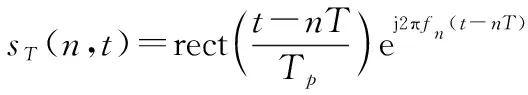
(1)

式中:∈,rect是定义在0到1之间的方波脉冲函数；为脉冲重复间隔；为脉冲宽度；=+为第个脉冲的载频,其中是起始载频、d为载频步进间隔；为随机化的频率码字,取值为∈{0,1,…,-1},其中为频点个数。假设雷达观测目标为一个复散射强度为的理想散射点,相对雷达作匀速直线运动,基于“停-跳”假设,该散射点回波可以表示为

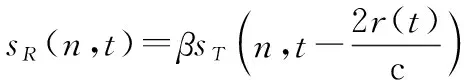
(2)

式中:c是光速；()为在时刻目标与雷达之间的径向距离,假设目标速度为则()=(0)+。对回波以Nyquist速率进行采样,在不同的粗分辨距离单元上分别处理采样数据。不失一般性,这里仅考虑同一个粗分辨单元内的目标,则回波序列为

()≈e-j4π(+)c

(3)

式中:和是目标的高分辨距离和速度。

假设在一个粗分辨单元内,雷达观测到有个目标,第个目标由个散射点组成,且同一目标上的散射点具有相同的速度。雷达的回波信号可以看成是不同目标对应回波的线性组合,可以表示为

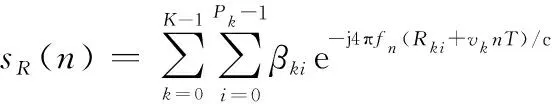
(4)

式中:、和分别是第个目标的第个散射点的散射强度、高分辨距离和速度。第12节将利用压缩感知理论对这些目标参数进行估计,挖掘一个相参处理间隔内的回波数据的结构特征,合成该粗分辨距离单元内目标的高分辨距离像(high range resolution profile, HRRP),提高目标重建的精度。

1.2 1 Bit块稀疏压缩感知模型

假设雷达回波被高斯噪声污染,将其可能观测的目标距离和速度参数分别均匀地离散化为和个格点,构造相应的目标的复散射系数向量为∈,其中只有少数元素非零,则捷变相参雷达压缩感知的数学模型可表示为

=+

(5)

式中：∈为雷达接收回波;是加性高斯白噪声向量,服从复高斯分布CN(0,),是噪声的方差,表示维的单位矩阵。=[,,…,]∈×为捷变相参雷达的观测矩阵。由于捷变相参雷达距离分辨力高,同一目标的不同散射点往往占据连续多个距离分辨单元,对应于待估计的目标向量上一系列成簇分布的非零元素,所以将向量按照不同的速度参数分成块,分块结构如下:

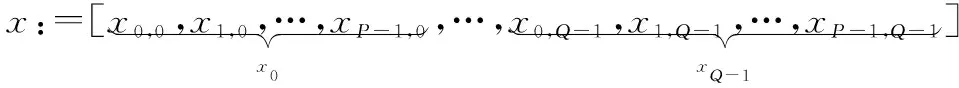
(6)

式中：被称为向量的第个子块,可以视作某一个目标的高分辨距离像。由于同一个粗分辨单元内目标个数往往较少,可以认为是一个块稀疏向量,即非零子块个数远小于。该块稀疏压缩感知模型在很多信号处理领域中有较广泛的应用,除了捷变相参雷达的扩展目标重构,还可以应用于窄带干扰剔除、空时自适应处理等。这里仅研究捷变频雷达因距离扩展而带来的块稀疏结构下的稀疏恢复问题,中每一块代表相应速度参数下的目标高分辨距离像。

为了压缩传输的数据量,在信号测量过程中对观测值进行量化,所以进一步研究量化压缩感知。量化压缩感知是压缩感知的一个重要分支,即将连续测量值映射为有限域上的离散值。1-Bit量化是对测量值量化的一种极限情况,即仅保留观测值的符号信息,此时观测模型改写为

=sign(+)

(7)

式中：复数域的sign函数为分别对复数的实部和虚部取符号。对1 Bit块稀疏压缩感知信号进行重构,一般转化为求最小范数的优化问题,由于1 Bit量化忽略了信号的幅度信息,将待重构信号的幅度归一化,即约束其在单位超球面上,该优化问题如下:

min||||,s. t.≥0, ||||=1

(8)

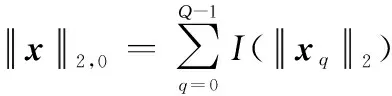
(9)

式中：(·)为指示函数。结合块稀疏和1 Bit压缩感知恢复算法,可以有效地求解上述问题。下面,进一步利用深度学习技术对捷变相参雷达目标向量快速重构。

2 1 Bit 块稀疏压缩感知重构算法

2.1 块稀疏BIHT算法

BIHT算法是在传统迭代硬阈值(iterative hard thresholding,IHT)算法的基础上进行修改,每次迭代过程中将目标函数微调,将残差的计算由绝对量改为了相对量。已知稀疏度为,其迭代计算公式为

+1=(-(sign()-))

(10)

式中：为可调步长；函数则表示将其中幅度最大的前个元素保留,其余元素置零。由于雷达场景具有块稀疏分布的特点,进一步将分块结构引入BIHT算法,得到block-BIHT(B-BIHT)算法,其具体步骤如下。

1-Bit观测值,雷达观测矩阵,最大的迭代次数,收敛容忍阈值;

初始化=,迭代次数=0;

计算残差=sign()-;

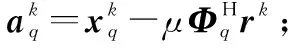
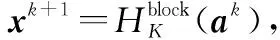
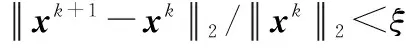
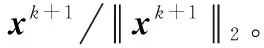
2.2 基于深度学习的快速重构网络

传统的阈值迭代算法计算量较高,所以考虑利用神经网络来求解稀疏恢复问题。其本质上就是求一个恢复算子,从数据中学习非常复杂的先验信息,加速迭代过程,减少运算量。一旦神经网络训练完成,结构和参数就都固定下来了,即迭代次数时一个固定值,每次恢复的计算量都是固定的,有望实现雷达对抗中的实时性要求。以Oracle-LISTA为例,其对传统软阈值迭代算法进行展开,第层的网络计算公式为

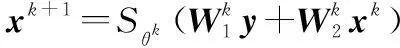
(11)

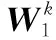
为了探究1-Bit压缩感知问题,修改了Ada-LISTA网络的残差计算方法,得到Binary Ada-LISTA(BAdaLISTA)此时网络的迭代公式为

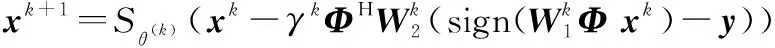
(12)

进一步加入分块的结构,并修改了目标函数和残差计算方法,改进非线性算子,提出了Block Binary Ada-LISTA(B-BAdaLISTA)网络,即对每个块分别做1-Bit量化后的梯度投影和带直通的软阈值算子,其相应的网络结构图如图1所示。

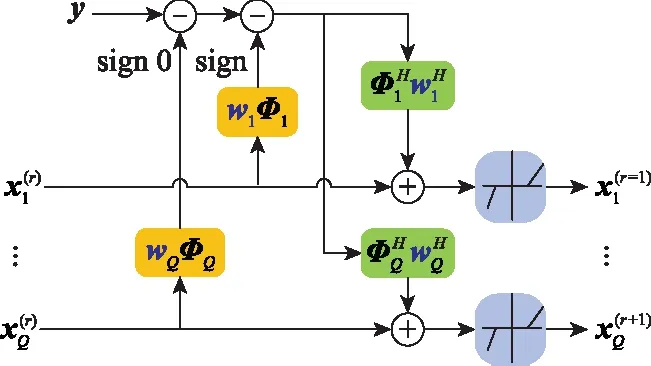
图1 块稀疏重建网络结构图Fig.1 Network structure of block-spase recovery network

3 实验结果及分析

3.1 无噪声情况下算法重建性能比较

为了验证所提重建算法性能的有效性,该文通过MATLAB、TensorFlow平台分别对BIHT、B-BIHT算法、BAdaLISTA、B-BAdaLISTA重建网络进行了实验仿真。在该实验中,捷变相参雷达系统参数设置如下:雷达的初始载频为9 GHz,雷达载频的跳频间隔d为30 MHz,雷达发射脉冲数=64,频点数=4,雷达脉冲重复间隔为200 μs。

相应的离散化高分辨距离、速度格点的范围和间隔如下。

高分辨距离格点的范围∈[-25 m,1.25 m],高分辨距离格点间隔Δ=125 m;速度格点的范围∈[833 m/s,9036 m/s],速度格点间隔Δ=13 m/s。

改变仿真的目标个数(即块稀疏度),每个目标的散射点个数为4,占据某一个速度通道下的所有高分辨距离格点。在每个块稀疏度下仿真100次,每次随机产生目标的散射点位置,幅度服从高斯分布。

比较了4种方法在1-Bit块稀疏下的性能:BIHT,B-BIHT,BAdaLISTA和B-BAdaLISTA。其中,前二者为传统阈值迭代算法,迭代次数上限为1 000;后二者为深度学习网络方法,层数均为10。纵坐标为衡量性能指标:归一化均方误差(normalized mean square error, NMSE)或击中率,横坐标为块稀疏度,仿真结果如图2所示。

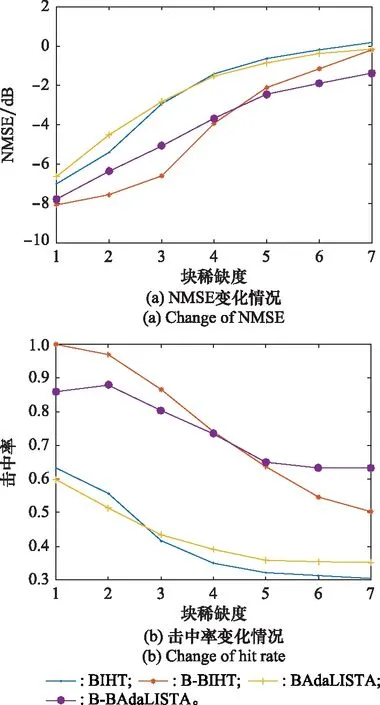
图2 无噪条件下恢复误差分析Fig.2 Recovery error analysis without noise

由图2可以看出,在相同实验条件下,对块稀疏度不同的捷变相参雷达信号进行1-Bit重构,B-BIHT算法和B-BAdaLISTA重建网络由于利用信号分块的结构特征,重构效果比BIHT算法和BAdaLISTA网络更好,同时B-BAdaLISTA重建网络计算量小,重建速度更快。

3.2 噪声情况下算法重建性能比较

在实际测量中,由于噪声的影响,会使1-Bit量化后的测量值符号发生变化,此时准确恢复原信号变得更加困难。因而进一步研究当信号受噪声影响时以上算法的重构效果。仿真的信噪比SNR∈[10 dB,50 dB],间隔为10 dB,注意此处的信噪比仅用来控制噪声标准差,即SNR=-20lg,其中为噪声幅值,如果要换算成每个散射点的真实信噪比,需要加上信号幅度对应的dB值,即SNR=SNR+20lg,其中为信号幅值

同样地,这里比较了4种方法在有噪条件下的性能:BIHT、B-BIHT、BAdaLISTA和B-BAdaLISTA。采用和无噪条件下相同的捷变相参雷达系统参数设置,分别针对不同的信噪比和块稀疏度进行仿真,每组块稀疏度和信噪比下仿真100次,根据噪声功率下随机产生噪声,以及根据目标个数随机产生散射点位置和幅度。结果如图3所示。

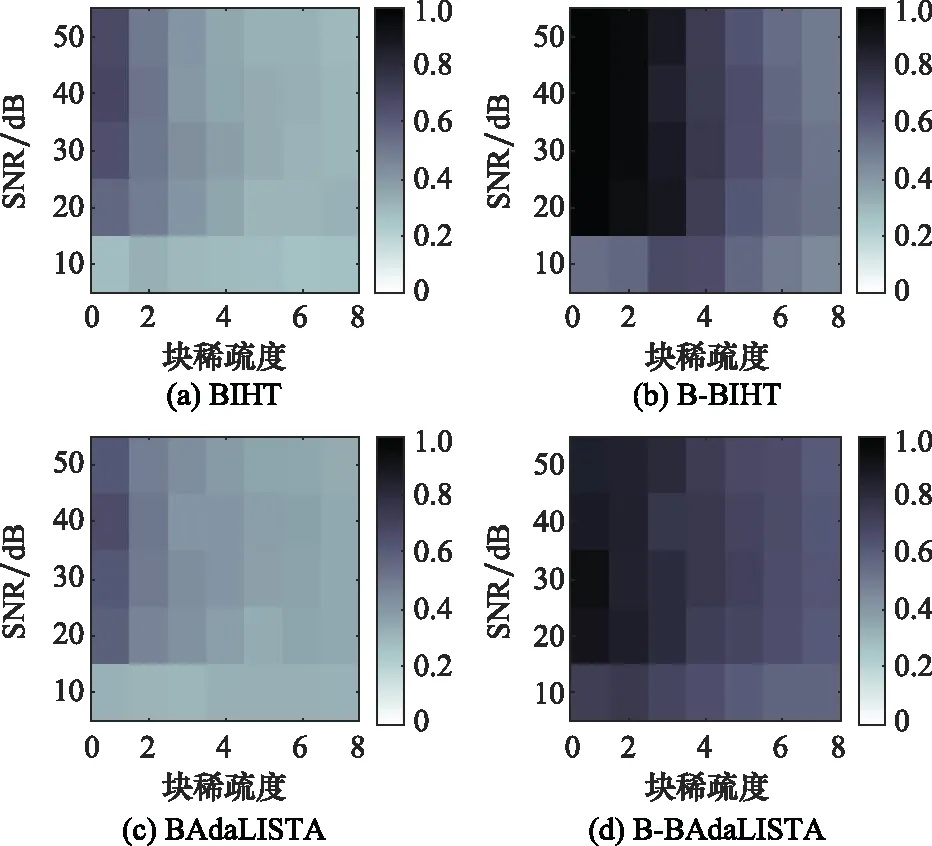
图3 有噪条件下恢复误差分析Fig.3 Recovery error analysis with noise

由图3可以看出,有噪条件下,考虑块稀疏结构的B-BIHT算法和B-BAdaLISTA重建网络的重构效果仍然明显优于BIHT算法和BAdaLISTA网络,且深度重建网络的收敛速度更快。

4 结 论

本文研究了捷变相参雷达的扩展目标稀疏恢复问题,结合块稀疏结构和1-Bit压缩感知恢复算法,构建基于深度学习的1-Bit块稀疏重构网络B-BAdaLISTA。仿真实验表明,在无噪和有噪情况下,B-BAdaLISTA重建网络收敛速度更快,计算复杂度固定,且恢复性能和同样基于块稀疏的迭代算法B-BIHT相当。