三角板中的相似三角形
2022-02-16耿恒考
耿恒考

三角板是我们数学学习中常用的文具,利用一副三角板可以编拟出好多经典的题目。下面,我们就一起来欣赏由三角板构造出的相似三角形“K型图”的应用问题。
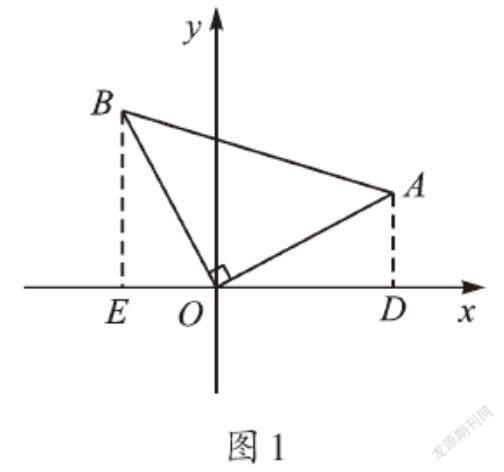
问题1 如图1,将含45°角的直角三角板,放在平面直角坐标系中。若点A的坐标为(2,1),求点B的坐标。
大家很容易想到,利用等腰直角三角形的性质,在图1中分别过点A、B作x轴的垂线段AD、BE,利用△OAD≌△BOE,证得BE=OD=2,OE=AD=1,从而得到点B的坐标为(-1,2)。
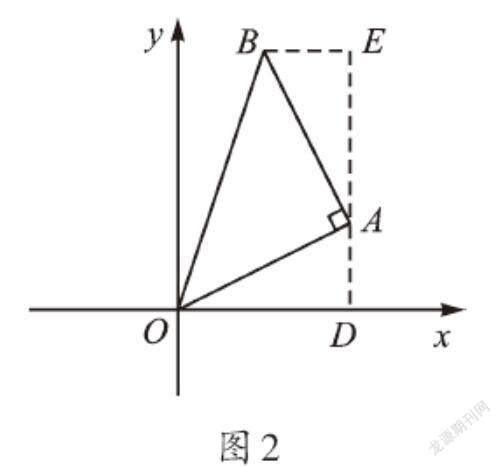
【拓展】如果将含45°角的直角三角板像图2这样放置,且点A的坐标为(2,1),如何求点B的坐标呢?我们可以用同样的方法,过点A作x轴的垂线AD,交x轴于点D,过点B作BE⊥AD,交DA的延长线于点E,利用△OAD≌△ABE,证得AE=OD=2,BE=AD=1,从而得到点B的坐标为(1,3)。
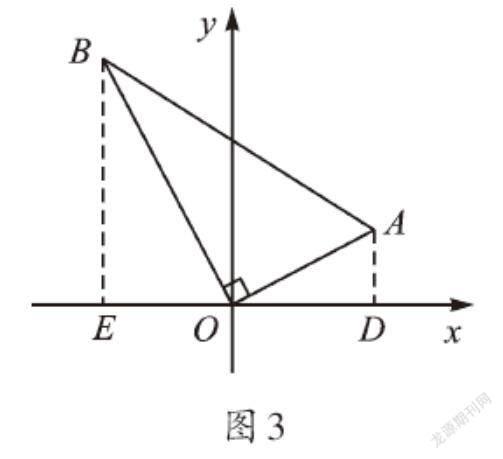
问题2 如图3,将含30°角的直角三角板,放在平面直角坐标系中。若点A的坐标为(2,1),求点B的坐标。
类比问题1,利用含30°角的直角三角形性质,如图3,分别过点A、B作x轴的垂线段AD、BE,利用△OAD∽△BOE,且相似比为1∶[3],证得BE=[23],OE=[3],从而得到点B的坐标为([-3],[23])。
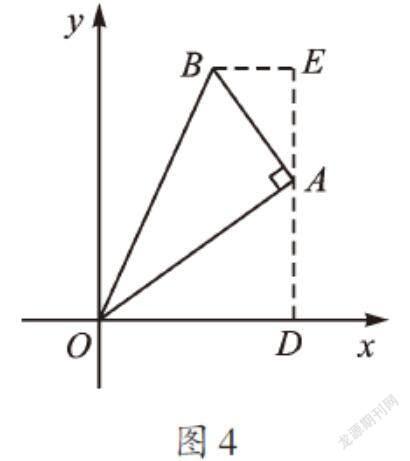
【拓展】如果将含30°角的直角三角板按如图4这样放置,且点A的坐标为(3,[3]),如何求点B的坐标呢?我们可以用同样的方法,过点A作x轴的垂线AD,交x轴于点D,过点B作BE⊥AD,交DA的延长线于点E,利用△OAD∽△ABE,且相似比为[3]∶1,证得AE=[3],BE=1,从而得到点B的坐标为(2,[23])。
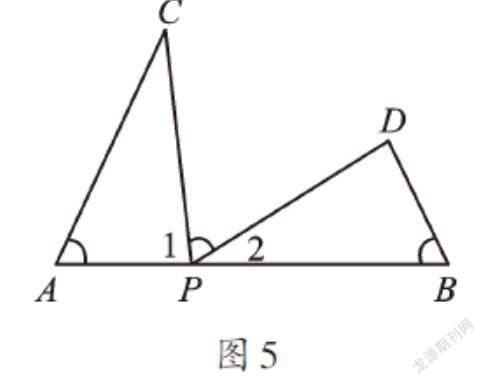
【感悟】观察以上几个问题中用三角板构造出的相似图形,不难发现一个共同特征:都有三个直角顶点在同一条直线上。我们经常把这样利用“一线三等角”来证明两个三角形相似的图形,称为“K型图”。其实“一线三等角”中的等角不一定是直角,锐角、钝角也都可以。
如图5,点P是线段AB上一点,点C、D在直线AB同侧,如果∠A=∠B=∠CPD=α,那么∠1+∠2=∠1+∠C=180°-α,可得∠C=∠2,再有∠A=∠B,证得△CAP∽△PBD。
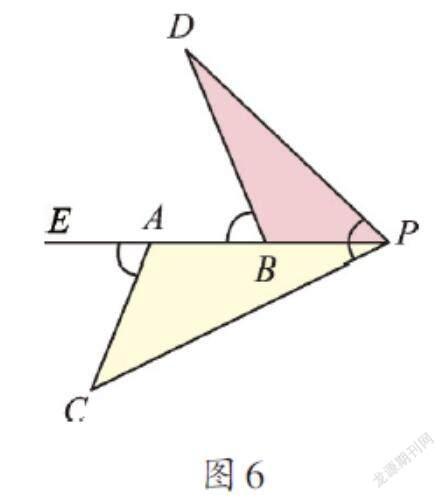
其实,上面问题中,如果点C、D分别在直线AB的异侧,只要有∠EAC=∠ABD=∠CPD=α,同样可以证得△CAP∽△PBD。如图6,请你尝试用上面图5的方法来证明这个结论。
利用“一线三等角”证明相似三角形“K型图”来解决问题,在各级各类考试中频繁出现。
问题3 如图7,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P。
(1)能否使你的三角板兩条直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由。
(2)再次移动三角板位置,使三角板直角顶点P在AD上移动,直角边PH始终通过点B,另一条直角边PF与DC延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请说明理由。
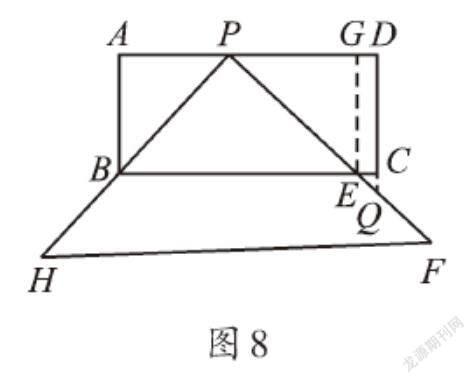
【解析】(1)因为“直角顶点P落在AD边上”“三角板两直角边分别通过点B与点C”,所以∠A=∠D=∠BPC=90°,可得相似三角形的“K型图”,据此列出关于AP的方程来解决问题;当然也可以在这三个直角三角形中利用勾股定理得到关于AP的方程来解决。
能。在Rt△ABP与Rt△DPC中,
AB2+AP2=PB2,PD2+CD2=PC2,
而在Rt△BPC中,PB2+PC2=BC2,
∴AB2+AP2+PD2+CD2=BC2。
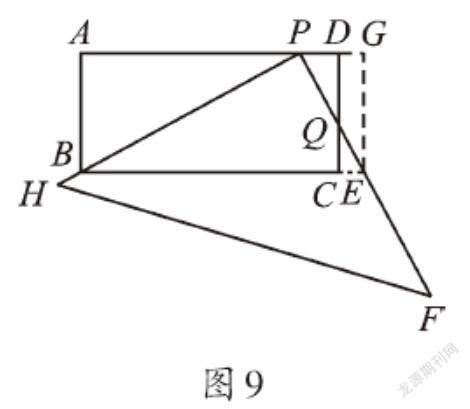
设AP=xcm,则PD=(10-x)cm(0 42+x2+(10-x)2+42=102, 解得x1=2,x2=8。 ∴AP=2cm或8cm。 (2)根据矩形的性质,判定△BAP∽△ECQ,△BAP∽△PDQ,列出方程求解即可。还可以过点E作EG⊥AD于点G,可得矩形ABEG,如图8,此时的问题(2)即转化为问题(1)的形式。用“K型图”列出关于AP的方程,或在三个直角三角形中利用勾股定理得到关于AP的方程,便可解决此题。 能。设AP=xcm,CQ=ycm(0 ∵四边形ABCD是矩形,∠HPF=90°, ∴△BAP∽△ECQ,△BAP∽△PDQ, ∴AP·CE=AB·CQ,AP·PD=AB·DQ, ∴2x=4y,x(10-x)=4(4+y), 得x2-8x+16=0,解得x1=x2=4, ∴AP=4cm。 【拓展】第(2)问改为“再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH始终通过点B,另一直角边PF与直线DC交于点Q,与直线BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由。” 【解析】根据现在的条件,需要考虑两种情况:①点Q在边DC的延长线上,见第(2)问的解析;②点Q在边DC上。 能。如图9,过点E作EG⊥AD,交AD延长线于点G,可得矩形ABEG,DG=EC=2cm,AG=BE=12cm。 利用△ABP∽△GPE,可得AB·GE=PG·AP。 设AP=xcm,则PG=(12-x)cm(0 ∴4×4=x(12-x),即x2-12x+16=0,解得x1=6+[25](不合题意,舍去),x2=6-[25]。 所以符合题意的AP长为4cm或(6-[25])cm。 【感悟】本题重点考查了相似三角形的“K型图”、勾股定理及矩形的性质的应用。一块三角板的运动,体现了数形结合、等价转化、分类讨论等数学思想方法的应用价值。 (作者单位:江苏省苏州中学园区校)
