基于模态分解的液环泵喷射器内非定常流动分析

蒋利杰，张人会，陈学炳,2，郭广强,2

基于模态分解的液环泵喷射器内非定常流动分析

蒋利杰1，张人会1※，陈学炳1,2，郭广强1,2

（1. 兰州理工大学能源与动力工程学院，兰州 730050；2. 甘肃省流体机械及系统重点实验室，兰州 730050）

为分析液环泵喷射器内复杂高速射流流场的瞬态流动特性，揭示射流尾迹涡脱落及激波自激振荡频率特征，该研究基于大涡模拟（Large Eddy Simulation, LES）数值模拟采用动态模态分解（Dynamic Mode Decomposition, DMD）和谱本征正交分解（Spectral Proper Orthogonal Decomposition, SPOD）方法对射流拟序结构进行时空解耦，对比分析2种模态分解方法在射流流动特征提取的差异性。研究结果表明，喷射器射流剪切层在与激波的干涉作用下呈现周期性振荡现象，且随着射流的演化其尾缘逐渐形成周期性脱落的尾迹涡。DMD和谱本征正交分解SPOD方法均能实现高速射流流场的解耦，且能够获得时空单频相干特征结构。主导频率1 250 Hz时，密度场DMD和SPOD 1阶模态均能反映激波及其与射流剪切层相互干扰形成的激波串结构特征；频率18 000 Hz时，DMD和SPOD动态模态则表征了射流尾缘周期性脱落的尾迹涡特征。相较于DMD方法，SPOD方法精准获取时空单频动态模态的同时能够反映出湍流射流的演变特征，而且有效避免了DMD基模态筛选时存在的不足。该研究基于LES数值模拟结果采用特征分解方法对喷射器内非定常流场进行了特征分解，为深入探索液环泵喷射器内复杂多物理耦合场奠定基础。

模态；频率；液环泵喷射器；SPOD；DMD；激波

0 引 言

喷射器是一种依靠高速流体的强剪切效应来传递介质能量和质量的设备，由于其在提高引射流体压力时不直接消耗机械能，结构紧凑，且与各种设备相连时系统简单等优点被广泛应用于石油化工、冶金、农业水电及真空等领域[1-3]，尤其在农业工程应用中，喷射器在深井自吸、药物喷洒等方面有重要的应用。但是喷射器内流场涉及激波、分离流动及边界层转捩等结构。其次，喷射器内高低速流体相互剪切、卷吸及掺混形成剪切涡及射流尾迹涡等复杂流动结构，导致其水力损失较大[4-7]。因此，对于喷射器内部复杂流场结构的解耦分析，揭示其内部相干结构的演变机理已成学者们关注的重点。

目前，针对流体机械内复杂拟序结构的解耦及演化机理的认识，学者们发展了多种特征分解方法，其主要包括本征正交分解（Proper Orthogonal Decomposition，POD）[8-10]，动力学模态分解（Dynamic Mode Decomposition, DMD）[11-14]和谱本征正交分解（Spectral Proper Orthogonal Decomposition, SPOD）[15-17]方法等。本征正交分解（POD）方法主要是通过对数据系统的特征分解进而获得流场的低阶高能基模态，但POD方法的不足之处在于其难以获得真实流场的单频模态[18-19]。谱本征正交分解（SPOD）方法一定程度弥补了POD方法的缺陷，在获得流场相干结构的同时兼顾流场频域特征。胡佳伟等[20]以压气机叶珊为目标，对比研究了不同特征分解方法在流动特征识别的差异性，结果表明在压气机湍流结构提取方面SPOD更具优势。童哲铭等[21]基于动力学模态分解（DMD）方法对叶道涡非定常流场进行相干结构的解耦与重构，分析表明DMD方法更有利于相干结构的流动机理分析。孙斐等[22]采用POD及DMD方法研究了进气道激波串振荡特性，并在此基础上预测了流场非定常演变特征，研究结果表明激波振荡是低频主导、多频耦合的复杂振荡现象。Schmidt等[23]讨论了SPOD方法及其在模态识别中的应用，并提出了一种基于Welch方法的估计谱密度张量的具体算法。Sieber等[24]在识别试验或数值模拟数据中的相干结构时使用了SPOD方法，以克服POD方法在提取多频率结构方面的缺陷。Vanierschot 等[25]利用POD和SPOD方法分析了环形旋流射流流场中螺旋相干结构的形状和动力学特性，结果表明相较于POD方法，SPOD方法能够从流场动力学信息中剥离出低能量结构。Lario等[26]通过降阶模型重构高维系统的潜在空间动力学，并对比分析POD及SPOD在射流特征结构提取的差异性。叶志贤等[27]基于PIV试验数据运用POD和DMD方法获得了合成射流激励器的内流场特性，结果表明运用POD和DMD方法进行的降阶过程在合成射流研究中的适用性。李虎等[28]通过POD和DMD分析了射流时序压力场和速度场，研究了啸声关联拟序流动结构的空间演化，精确定位了轴对称模态啸声的声源位置。Aaron等[29]建立了谱本征正交分解和动态模态分解之间的关系，并通过一湍流射流案例对其进行验证分析，结果分析表明SPOD模态所代表的是与DMD模态具有相同意义上的动态结构，但也最优地解释了湍流的统计变异性。

为进一步揭示液环泵喷射器内射流相干结构的演变规律及频率特征，本研究采用商业模拟软件对喷射器内流场进行数值模拟，基于大涡模拟（Large Eddy Simulation, LES）数值模拟结果采用DMD及SPOD方法对喷射器内非定常湍流射流场进行解耦分析及重构，并对比分析2种特征分解方法在射流流动特征识别的差异性。

1 数值计算

1.1 数值计算模型

本研究以KLRC-200气体喷射器为研究对象，其基本参数如表1。喷射器计算域包括喷嘴、吸入室、混合室及扩散管（图1a），对其采用结构化网格进行离散（图1b）。采用5套不同网格数量方案进行无关性检验，不同方案网格数分别为5 498 906、6 554 992、7 355 682、9 917 080、11 481 644，如图2所示，随着网格数的增加喷射器引射流量逐渐趋于稳定。与此同时，基于Pope’s准则对该网格精度进一步进行验证，验证结果表明当前网格能捕获90%以上的解析湍动能，而Pope’s准则认为解析湍动能占比大于80%则说明网格满足精度要求。因此，综合考虑计算资源及网格精度的前提下选用网格数为9 917 080作为后续数值研究。

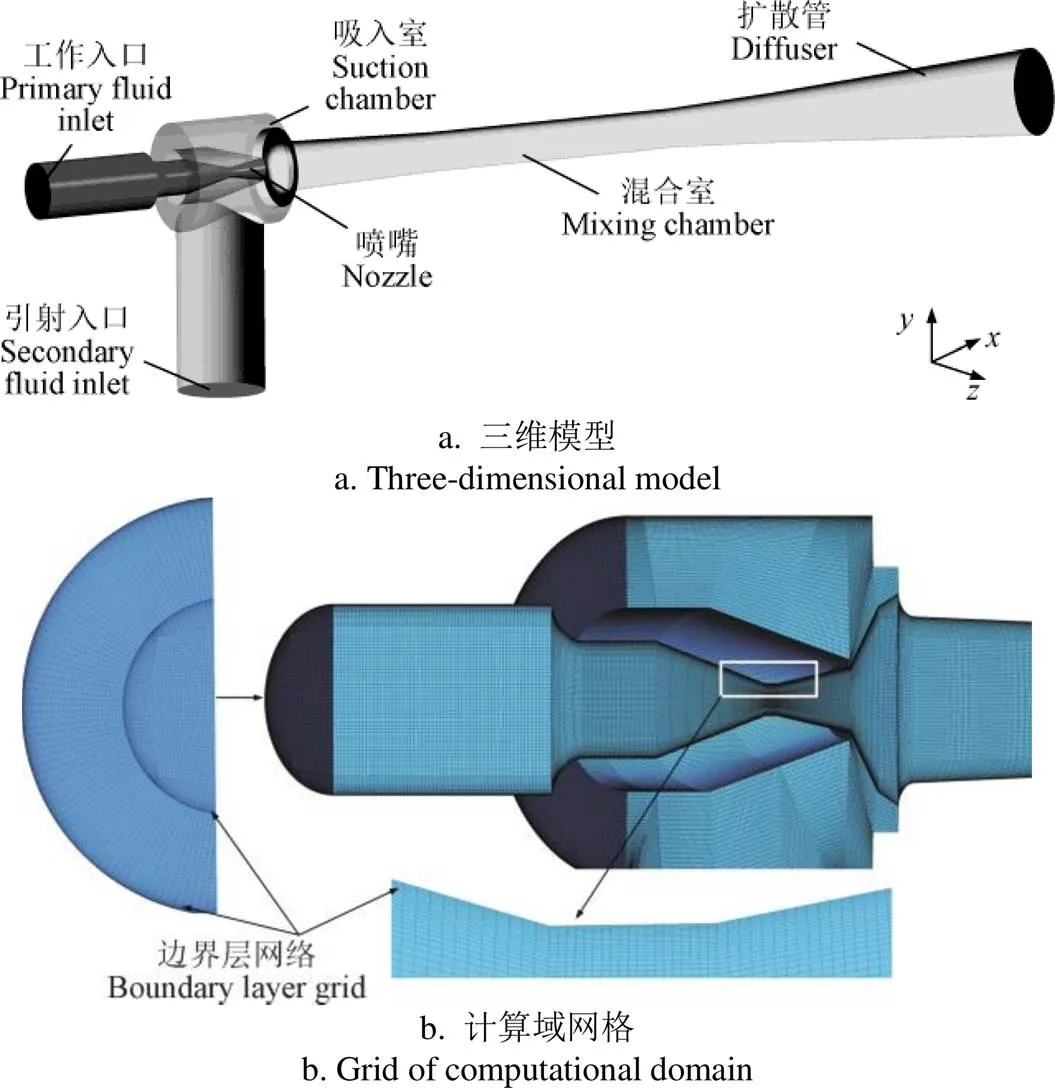
图1 喷射器几何模型及网格

图2 网格无关性验证

表1 喷射器基本参数

1.2 数值边界条件

考虑气体的可压缩性，基于有限体积方法的密度显式耦合求解器进行数值模拟，无黏通量项离散选用Roe-FDS通量差分分裂格式，动量和能量方程的离散采用二阶迎风格式，采用1阶精度的隐式格式处理时间项。尺度解析模型选用LES模型，亚格子模型选用Smagorinsky-Lilly模型。工作流体及引射流体进口采用压力进口边界，出口则采用压力出口边界，绝热无滑移壁面。时间步长选用∆=1×10-6s，与此同时，收敛残差设为1×10-6，为保证数值结果收敛，非定常计算迭代12 000步直至喷射器进出口监测点流量达到稳定，其次收敛残差达到1×10-4。

1.3 试验设备及方法

基于课题组搭建的液环泵喷射器测试平台进行喷射器外特性试验，液环泵喷射器测试系统如图3所示，该系统主要由液环泵、喷射器、管路系统及动力控制系统等组成。试验测试时首先启动液环泵，待其运行稳定后开启喷射器，通过调整阀门14的开度来控制引射入口真空度进行变工况测量，引射入口真空度由压力表11测量，引射流量由孔板流量计3测量，工作入口流量由涡街流量计10测量；包含因子为2时，孔板流量计3的综合不确定度计扩展不确定度为0.4%和0.8%，而涡街流量计10的综合不确定度计扩展不确定度分别为0.2%和0.4%。

1.水槽 2.控制柜 3.孔板流量计 4.供水泵 5.电动机 6.液环泵 7.气液分离罐 8.喷射器 9.流量控制阀 10.涡街流量计 11.压力表1 12.压力表2 13.闸阀 14.压力调节阀1 15.压力调节阀2

对不同引射真空度工况下（0.080、0.059、0.046、0.024、0.004 MPa）喷射器内流场进行数值模拟，并对其结果进行试验验证。引入均方根误差（RMSE）判定模拟数值与试验结果误差，其误差定义如式（1）。

图4为液环泵喷射器引射真空度随引射流体进口流量变化的数值模拟与试验结果对比，从图中可以看出，LES数值模拟结果略高于试验值，整体变化趋势一致，但也存在一定的误差，其主要原因是数值模拟未考虑泵轴向间歇泄漏的影响且当前网格仍难以捕获到足够小尺度的结构，其均方根误差为0.53%，总体上喷射器引射流量数值模拟结果与试验值吻合良好。

式中QCFD为数值模拟吸气量，m3/s；QEXP为试验吸气量，m3/s；n为试验次数。

2 模态分解方法

喷射器内存在复杂多物理场的相互耦合现象，为了对其内复杂特征结构进行解耦分析，本研究提出采用DMD及SPOD特征分解方法对数值模拟稳定后不同瞬态时刻密度场数据进行特征解耦分析。

2.1 动态模态分解（DMD）

DMD方法最早是由Schmid[30]提出的，从大量的样本数据中提取动力学信息是DMD方法的本质，由个瞬态快照构成样本矢量集，且相邻快照采样间隔为∆。

假定v+1与v存在线性映射关系，其中列向量v表示第个时刻的流场快照。

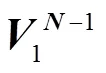
经特征分解可得矩阵的特征值，且任一模态及对应的增长率和频率可表示为

式中φ为第个模态，y为第个特征向量，其对应特征值为λ。

模态振幅被定义为

式中为特征向量，则任意时刻流场可表示为

2.2 谱本征正交分解（SPOD）

SPOD方法最早是由Sieber提出的[24]，其采用Welch方法对样本矩阵进行分块，可得具有相互重叠快照的分块矩阵：

此时，第个分块的第个快照可表示为

式中=1,2,...,N，w是窗口函数的节点值，则频率为f的相关矩阵可表示为

式中=Δ/()，则频率为f的交叉谱密度相关矩阵可表示为

式中为正定Hermitian矩阵。因此，求解各频率交叉谱密度相关矩阵的特征值问题即可求得SPOD模态为

3 结果与分析

3.1 非稳态特征分析

待数值模拟稳定后选取引射真空度为0.08 MPa工况下流场开展喷射器内密度场及激波结构特征分析，图5为喷射器轴向涡量分布，从图中可以看出，开尔文-亥姆霍兹（Kelvin-Helmholtz）不稳定诱导射流高低速流体间形成强烈剪切涡，与此同时，由于射流的强剪切作用导致圆柱剪切层周围形成涡带，且在激波的作用下射流核心区域内呈现出规则分布的波状结构。随着射流不断向下游发展，可以看到射流剪切层在径向存在明显的周期性振荡现象，这是激波的自激振荡所致。此外，可以观察到射流核心区内两股流体并未发生混合，直到射流尾缘逐渐开始混合。

为了进一步分析喷射器内流体混合特性，分别选取混合室内不同横截面P1、P2和P3，如图5中所示，对其上流场进行对比分析。

注：P1、P2、P3分别表示不同位置处横截面。

图6为喷射器混合室内不同横截面上涡量分布，由图可以看出不同截面涡量分布存在较大差异，相较于P3截面，P1和P2截面位于射流核心区，其剪切层内存在明显的高强度涡量区，且沿着流向方向射流核心区域逐渐增大。此外，P1、P2截面剪切层周围存在不同尺度的旋涡即图5中的涡带结构，引射流体在强剪切卷吸作用下逐渐向射流核心区靠拢，但圆柱剪切层断面并未受到引射流体的冲击绕流作用而发生变形，表明此时中心射流并未与低速引射流体发生混合。随着射流不断向下游的发展，射流剪切涡受到引射流体涡带的绕流作用，其形状发生变化随后二者相互作用导致剪切涡在射流尾缘脱落。可以看到P3截面处流动逐渐变得复杂，射流剪切涡和涡带结构相互作用随即形成不同尺度的尾迹涡，与此同时，工作流体和引射流体开始发生不同程度的混合。

图6 不同横截面涡量分布

3.2 DMD分解

由3.1节分析可知，喷射器混合室内流动较为复杂，存在多物理场的相互耦合，因此，为了进一步揭示高速射流流场演化特性，采用DMD及SPOD方法对喷射器轴面密度场进行特征分解。待数值模拟计算稳定后，以4×10-6s为间隔，选取600个瞬态时刻密度场作为快照集进行特征分解。图7为瞬态密度场DMD特征分解所得特征值及频率振幅分布。

注：0、1、2、3、4及A分别表示密度场0阶模态、1阶模态、2阶模态、3阶模态、4阶模态及模态A。

从图7a中可以看出，绝大多数特征值位于单位圆附近，仅少数特征值位于单位圆内，这一分布规律表明射流密度场特征分解所得模态基本多为稳定模态和周期性模态。选取前4阶主导模态和一耗散模态进行特征分析，如图中红色标记所示，其中0阶模态为静态模态其频率为0且振幅最高，表征了非定常流动的基本稳态结构；1～4为前4阶主导模态，可以看见1～4阶模态均位于单位圆附近且其频率分别为1 250、17 500、18 000和20 200 Hz；此外从图7b可以看出频率为24 300 Hz的模态具有较高的振幅且其特征值分布不在单位圆上，为了便于后续特征结构分析将其记为模态A。

由前5阶模态对第一时刻瞬态密度场进行预测分析，其和数值模拟结果对比如图8所示，从图中可以看出，前5阶模态能够很好的实现目标时刻流场的精确预测，其均方根误差和绝对百分比误差分别为3.5%和1.5%。

图9为DMD静态0阶模态分布，其所涵盖的能量占比最高，表征了非定常流动的基本稳态结构。由图可以看出静态模态空间分布近似时均流场，喷嘴渐阔段出口形成型激波结构，同时在射流核心区内呈现出由激波及剪切层相互干扰形成的激波串结构。可见，密度静态模态反映了高速射流区内的激波及其与射流剪切层的干扰特征。

图9 密度场DMD 0阶模态分布

图10为DMD密度1～3阶模态分布，可以看出各阶模态空间分布存在显著差异。1阶模态对应频率为1 250 Hz，其喷嘴内及射流核心区出现了型结构及不连续交替分布的特征结构，这与图8密度瞬态流场分布具有相似性，可见1阶模态表征超音速射流形成的激波特征，且其对应频率反映了激波的自激振荡频率。激波自激振荡即激波在恒定压力下受到激波和边界层干扰的影响表现出的一种非定常特性[31]。相较于1阶模态，2阶和3阶模态尺度明显有所减小，但均呈现出相似的反对称相间分布结构，且二者存在一定的相位差。结合图5轴面涡量分布，随着时间推移，剪切涡逐渐耗散并在射流尾缘不断周期性拉伸及脱落，由此可知密度场2阶和3阶模态表征了射流剪切涡拉伸、脱落的流场特征，且其相应频率17 500和18 000 Hz则反映了射流尾迹涡的脱落频率。

图10 密度场DMD 1～3阶模态分布

由图7a特征值分布可知，DMD模态多为稳定和周期性模态，为了深入分析各模态流场的稳定性，对其相应模态系数的演化规律进行对比分析，如图11所示。

图11 密度场DMD模态系数变化

可以看出各阶模态均表现出明显的周期性特征，其中1阶模态振幅最大且较稳定，表明1阶模态捕获的流场特征稳定且对流场贡献最大。而2阶和3阶模态脉动频率较大且幅值依次减小，因此其反映了射流尾迹涡结构的逐渐耗散及脱落特征。

在DMD特征分解中，耗散模态特征值位于单位圆内为周期性模态，但其对非定常流场的发展并非起主导作用。图12为耗散模态A随时间的演化规律，由图可知初始时刻模态A具有较高的能量，但随着时间的推移该模态能量迅速衰减耗散，由此可见耗散模态对非定常流场的发展有着极少的贡献。

图12 密度模态A演化规律

3.3 SPOD分解

采用Welch方法将600个瞬态时刻数据组成的快照集分为5块，各块含有200个快照且块重叠率为50%。图13为SPOD分解特征值能谱图，各频率特征值呈降序排列，由图可以看出，1阶模态能量明显高于其余各模态，且在低频1 250 Hz及高频17 500及18 000 Hz范围内模态能量具有显著的峰值，可见该频率下模态为流场主导模态。

图14为1 250 Hz及18 000 Hz峰值频率对应的SPOD单频模态分布。频率1 250 Hz时，SPOD一阶模态同DMD 1阶模态结构极其相似，均捕捉到了喷嘴内的激波及射流核心区内的激波串结构。同样，频率为18 000 Hz时，SPOD 1阶模态射流尾缘呈现出与DMD 2阶模态相似的反对称且交替分布的特征结构。此外可以看到，SPOD同一频率下2阶模态相较于1阶模态其特征尺度更小且结构数量变多，这一特征表明湍流射流在发展过程中不断的演化成多种不同尺度的流动，这一结果和Aaron等[29]的结论一致。综上可知，SPOD模态分解除了包含DMD方法的诸多优点之外，能更进一步的反映湍流射流的演化特性，且不存在DMD筛选主导模态等的问题。因此，相较于DMD特征分解，SPOD在湍流相干结构提取方面更具优势。

图13 密度场谱本征正交分解能谱图

图14 不同频率密度场谱本征正交分解模态分布

4 结 论

1）喷射器内高低速流体间由于开尔文-亥姆霍兹（Kelvin-Helmholtz）不稳定性诱导形成强烈的剪切涡，在激波与剪切层的干扰作用下射流核心区流场呈现出规则分布的波状结构。低速流体依靠剪切涡的卷吸逐渐向中心高速射流区靠拢，并在射流尾缘开始与高速工作流体发生混合。

2）动力学模态分解（Dynamic Mode Decomposition, DMD）方法能够准确获取喷射器内射流流场的单频特征结构，1阶模态表征激波及其与射流剪切层相互干扰形成的激波串特征结构。2阶及3模态则反映了射流尾迹涡的周期性拉伸及脱落。与此同时，DMD方法能够实现目标流场的精准预测，其均方根及绝对百分比误差分别为3.5%和1.5%。

3）谱本征正交分解（Spectral Proper Orthogonal Decomposition, SPOD）方法能够将流场分解为同一频率下的模态排序集。非定常流场主导频率为1250、17 500和18 000 Hz，其分别对应于低频激波振荡频率及高频段的尾迹涡脱落频率。相较于DMD分解，SPOD方法能够获取射流单频相干结构特征的同时反映出湍流射流的演化特性。

[1] 李熠桥，沈胜强，张梦超. 非平衡凝结超音速蒸汽喷射器RSM模型壁面函数法比较与分析[J]. 工程热物理学报，2021，42(9)：2321-2325.

Li Yiqiao, Shen Shengqiang, Zhang Mengchao. Near-wall treatments of non-equilibrium condensing rsm model of a supersonic steam ejector[J]. Journal of Engineering Thermophysics, 2021, 42(9): 2321-2325. (in Chinese with English abstract)

[2] 俞梦琪. 喷射器内部流动和激波特性的数值模拟和可视化实验研究[D]. 大连：大连海事大学，2019.

Yu Mengqi. Numerical and Visual Experimental Investigation on the Fluid Flow and Shock Wave Characteristics Inside the Ejector[D]. Dalian: Dalian Maritime University, 2019. (in Chinese with English abstract)

[3] 祝银海，姜培学. 旁通型喷嘴喷射器的环隙结构对性能的影响[J]. 工程热物理学报，2015，36(11)：2324-2327.

Zhu Yinhai, Jiang Peixue. Investigation of the influence of Annular cavity structure on the bypass ejector performance[J]. Journal of Engineering Thermophysics, 2015, 36(11): 2324-2327. (in Chinese with English abstract)

[4] Jiang L J, Zhang R H, Chen X B, et al. Analysis of the high-speed jet in a liquid-ring pump ejector using a proper orthogonal decomposition method[J]. Engineering Applications of Computational Fluid Mechanics, 2022, 16(1): 1382-1394.

[5] 王晓冬，付强，易舒，等. 蒸汽喷射制冷系统喷射器工作特性的实验研究[J]. 东北大学学报（自然科学版），2017，38(12)：1744-1747.

Wang Xiaodong, Fu Qiang, Yi Shu, et al. Experimental investigation of operating characteristics of ejector in steam jet refrigeration system[J]. Journal of Northeastern University (Natural Science), 2017, 38(12): 1744-1747. (in Chinese with English abstract)

[6] 杨勇，李熠桥，沈胜强，等. 蒸汽喷射器中的激波效应[J].工程热物理学报，2014，35(7)：1419-1423.

Yang Yong, Li Yiqiao, Shen Shengqiang, et al. Shock effect in the steam ejector[J]. Journal of Engineering Thermophysics, 2014, 35(7): 1419-1423. (in Chinese with English abstract)

[7] 张孝石，许昊，王聪，等. 水流冲击超声速气体射流实验研究[J]. 物理学报，2017，66(5)：197-207.

Zhang Xiaoshi, Xu Hao, Wang Cong, et al. Experimental study on underwater supersonic gas jets in water flow[J]. Acta Physica Sinica[J]. 2017, 66(5): 197-207. (in Chinese with English abstract)

[8] Shinneeb A M, Balachandar R, Bugg J D. Analysis of coherent structures in the far-field region of an axisymmetric free jet identified using particle image velocimetry and proper orthogonal decomposition[J]. Journal of Fluids Engineering, 2008, 130(1):151-163.

[9] 王燕，程杰，贾安，等. 基于本征正交分解的水平轴风力机非定常尾迹特性分析[J]. 农业工程学报，2022，38(7)：69-77.

Wang Yan, Cheng Jie, Jia An, et al. Unsteady wake analysis of horizontal wind turbine using proper orthogonal decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 69-77. (in Chinese with English abstract)

[10] 王谋远，苏纬仪，孙斐，等. 高超声速进气道宽范围工作多场耦合效应及快速预测研究[J/OL]. 推进技术：2022，1-18[2022-10-11].http://kns.cnki.net/kcms/detail/11.1813.V.20220217.1139.002.html

Wang Mouyuan, Su Weiyi, Sun Fei, et al. Multi-field coupling effects and rapid prediction of hypersonic inlet operating in a wide range[J/OL]. Journal of Propulsion Technology, 2022, 1-18[2022-12-11]. (in Chinese with English abstract)

[11] 张人会，王少华，Osman Juma S A. 螺旋轴流式油气混输泵导叶内非定常流动DMD分析[J]. 农业机械学报，2020，51(9)：118-126.

Zhang Renhui, Wang Shaohua, Osman Juma S A. Transient gas-liquid flow in helical axial pump diffuser and its DMD analysis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(9): 118-126. (in Chinese with English abstract)

[12] Zang B, Vevek U S, New T H. Some insights into the screech tone of under-expanded supersonic jets using dynamic mode decomposition[J]. Journal of Aerospace Engineering, 2021, 34(4): 04021034.

[13] Jeyakumar S, Kandasamy J, Karaca M, et al. Effect of hydrogen jets in supersonic mixing using strut injection schemes[J]. International Journal of Hydrogen Energy, 2021, 46(44): 23013-23025.

[14] Liu M, Tan L, Cao S. Method of dynamic mode decomposition and reconstruction with application to a three-stage multiphase pump[J]. Energy, 2020, 208: 118343.

[15] 郭婷，夏超，储世俊，等. 不同转向架构型对高速列车列车风及非定常尾迹的影响[J]. 空气动力学学报，2022，40(2)：94-104.

Guo Ting, Xia Chao, Chu Shijun, et al. Impact of different bogie configuations on slipstream and unsteady wake of a high-speed train[J]. Acta Aerodynamica Sinica, 2022, 40(2): 94-104. (in Chinese with English abstract)

[16] Chu S, Xia C, Wang H, et al. Three-dimensional spectral proper orthogonal decomposition analyses of the turbulent flow around a seal-vibrissa-shaped cylinder[J]. Physics of Fluids, 2021, 33(2): 025106.

[17] Kadu P A, Sakai Y, Ito Y, et al. Application of spectral proper orthogonal decomposition to velocity and passive scalar fields in a swirling coaxial jet[J]. Physics of Fluids, 2020, 32(1): 015106.

[18] 张人会，陈学炳，郭广强，等. 低比转数离心泵叶轮内流场重构与模态分析[J]. 农业机械学报，2018，49(12)：143-149.

Zhang Renhui, Chen Xuebing, Guo Guangqiang, et al. Reconstruction and modal analysis for flow field of low specific speed centrifugal pump impeller[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(12): 143-149. (in Chinese with English abstract)

[19] 毛宁，康灿，周明明. 淹没射流流场结构的POD分析及空化云演化[J]. 工程热物理学报，2019，40(9)：2036-2042.

Mao Ning, Kang Can, Zhou Mingming. POD Analysis of submerged jet structure and cavitation on cloud evolution[J]. Journal of Engineering Thermophysics, 2019, 40(9): 2036-2042. (in Chinese with English abstract)

[20] 胡佳伟，王掩刚，刘汉儒，等. 压气机叶栅非定常分离流动的模态分解方法对比研究[J]. 西北工业大学学报，2020，38(1)：121-129.

Hu Jiawei, Wang Yangang, Liu Hanru, et al. Comparative study on modal decomposition methods of unsteady separated flow in compressor cascade[J]. Journal of Northwestern Polytechnical University, 2020, 38(1): 121-129. (in Chinese with English abstract)

[21] 童哲铭，辛佳格，童水光. 基于动态模态分解的叶道涡非定常解耦与重构[J]. 中国机械工程，2022，33(7)：769-776.

Tong Zheming, Xin Jiage, Tong Shuiguang. Decoupling and reconstruction of unsteady flow field of inter blade vortices based on DMD[J]. China Mechanical Engineering, 2022, 33(7): 769-776. (in Chinese with English abstract)

[22] 孙斐，苏纬仪，侯强，等. 进气道激波串振荡的模态分解及快速预测[J]. 航空动力学报，2021，36(5)：1040-1051.

Sun Fei, Su Weiyi, Hou Qiang, et al. Modal decomposition and rapid prediction of shock train oscillation for inlet[J]. Journal of Aerospace Power, 2021, 36(5): 1040-1051. (in Chinese with English abstract)

[23] Schmidt O T, Colonius T. Guide to spectral proper orthogonal decomposition[J]. AIAA Journal, 2020, 58(3): 1023-1033.

[24] Sieber M, Paschereit C O, Oberleithner K. Spectral proper orthogonal decomposition[J]. Journal of Fluid Mechanics, 2016, 792: 798-828.

[25] Vanierschot M, Müller J S, Sieber M, et al. Single-and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow[J]. Journal of Fluid Mechanics, 2020, 883(A31):1-30.

[26] Lario A, Maulik R, Schmidt O T, et al. Neural-network learning of SPOD latent dynamics[J]. Journal of Computational Physics, 2022, 468: 111475.

[27] 叶志贤，方元祺，邹建锋，等. 合成射流激励器流场PIV实验及模态分析[J]. 推进技术，2021，42(2)：258-271.

Ye Zhixian, Fang Yuanqi, Zou Jianfeng, et al. Synthetic jet actuator piv experiments and modal analysis[J]. Journal of Propulsion Technology, 2021, 42(2): 258-271. (in Chinese with English abstract)

[28] 李虎，罗勇，韩帅斌，等. 基于模态分解的轴对称超声速射流啸声产生位置数值分析[J]. 力学学报，2022，54(4)：975-990.

Li Hu, Luo Yong, Han Shuaibin, et al. Numerical study on the generation position of screech tone in axisymmetric supersonic jet based on modal decomposition[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(4): 975-990. (in Chinese with English abstract)

[29] Aaron T, Schmidt O T, Tim C. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis[J]. Journal of Fluid Mechanics, 2017, 847: 821-867.

[30] Schmid P. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5-28.

[31] 杨基明，李祝飞，朱雨建，等. 高超声速流动中的激波及相互作用[M]. 北京：国防工业出版社，2019.

Unsteady flow in liquid ring pump ejector using mode decomposition

Jiang Lijie1, Zhang Renhui1※, Chen Xuebing1,2, Guo Guangqiang1,2

(,730050,;2.,,730050,)

A liquid-ring pump is one of the commonly-used rotating positive-displacement machines. This study aims to analyze the transient flow characteristics of complex high-speed jet flow field in the ejector of liquid ring pump, in order to reveal the frequency characteristics of jet wake vortex shedding and shock wave self-excited oscillation. Dynamic Mode Decomposition (DMD) and Spectral Proper Orthogonal Decomposition (SPOD) were used to decouple the jet coherent structure using Large Eddy Simulation (LES). Two modes of decomposition were compared to extract the jet flow features. The results show that the vortex band was formed in the mixing chamber for the strong shear effect of the jet shear layer. The shape of shear vortex was changed to fall off at the trailing edge of jet, due to the influence of vortex zone. The periodic oscillation was found in the shear layer of the jet under the interaction with the shock waves. As such, the periodic shedding wake vortex was gradually formed at the trailing edge of the jet. The decoupling analysis of the high speed jet flow field was also achieved to obtain the spatiotemporal single frequency coherence structure using DMD and SPODs. The flow field at the target time was accurately predicted using the first five-order DMD density modes, where the Root Mean Square Error (RMSE) and absolute percentage error were 3.5% and 1.5%, respectively. The DMD mode with the frequency of 0 presented the highest energy proportion, indicating the steady-state characteristics of unsteady flow. The first order DMD mode with the frequency of 1 250 Hz was utilized to capture the shock wave and the shock string structure that formed by the interaction between the shock wave and the jet shear layer. The spatial structure shared the periodic evolution characteristics of jet shear vortexes in the second and third order DMD modes with the frequencies of 17 500 and 18 000 Hz, respectively. In addition, there was the similarity of spatial structure in the DMD modes in the high frequency band, indicating a multi-frequency coupling shedding of jet wake vortexes. The dominant mode of SPOD was better reflected by the frequency amplitude. The characteristic values of SPOD were arranged in the descending order at each frequency. In the frequency of 1 250 Hz, the first order SPOD mode also reflected the shock wave structure similar to the first order DMD mode. Meanwhile, there was the similar characteristic structure in the SPOD and DMD mode in the high frequency band. The characteristic scale of the second order SPOD mode was smaller than that of the first order mode. It infers that the coherent structure of turbulent jet was constantly evolved into the multi-scale flows during the process of development. The SPOD can be expected to accurately obtain the spatiotemporal single frequency dynamic modes for the evolution characteristics of turbulent jet, compared with the DMD. In addition, the SPOD can also effectively avoid the DMD in the selection of dominant mode. Therefore, the SPOD has more advantages than the DMD in the coherent structure decoupling analysis of turbulent jets.

mode; frequency; liquid ring pump ejector; SPOD; DMD; shock wave

10.11975/j.issn.1002-6819.2022.21.003

TH38

A

1002-6819(2022)-21-0016-08

蒋利杰,张人会,陈学炳，等. 基于模态分解的液环泵喷射器内非定常流动分析[J]. 农业工程学报，2022，38(21)：16-23.doi：10.11975/j.issn.1002-6819.2022.21.003 http://www.tcsae.org

Jiang Lijie, Zhang Renhui, Chen Xuebing, et al. Unsteady flow in liquid ring pump ejector using mode decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(21): 16-23. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.21.003 http://www.tcsae.org

2022-09-13

2022-10-12

甘肃省重点研发计划（21YF5GA077）；国家自然科学基金（51979135，52269021）

蒋利杰，博士研究生，研究方向为流体机械内流动分析。Email：jianglijie_jlj@163.com

张人会，博士，教授，博士生导师，研究方向为水力机械内部流动及性能优化。Email：zhangrhlut@163.com