车用增程器扭振特性优化与鲁棒性分析

吕梦杨，韩志玉，吴振阔

（同济大学 汽车学院，上海201804）

0 概述

现今能源与环境问题日益严峻，在国家节能减排相关政策法规的引导下，发展新能源汽车成为车企的必然选择。其中增程式电动汽车由于其续驶里程长、低温适应性好与成本低廉等优势，受到了广泛关注［1］，目前已有多款该类车型投入市场。

增程器是增程式电动汽车的核心部件，其主要由内燃机与起动发电一体机（integrated starter generator，ISG）组成，二者轴系的匹配与连接是增程器集成设计的一个重要问题。不合理的结构与参数设计将导致轴系扭转振动特性恶化，影响增程器安全平稳运行。双质量飞轮是一种较新型的扭转减振器，它可以有效隔离两端的扭矩波动并调整轴系低阶固有频率，逐步在汽车传动轴系中获得应用［2］。这一结构的引入改善了轴系扭振特性，但还需要参数匹配设计实现进一步优化。此外，由于制造误差或者工作环境变化，可能会使轴系扭振特性偏离设计预期，为此需要评估其鲁棒性。

目前国内外的相关研究主要集中于传统内燃机汽车传动轴系，对于增程器轴系扭转振动研究较少，且现有研究多为扭振特性的时频分析，对其优化与鲁棒性分析相对较少。文献［3］中分析了增程器轴系在稳态与瞬态典型工况下的扭振特性，发现轴系扭振主要受发动机与发电机激励力矩波动及系统共振影响。文献［4］中分析了双质量飞轮的关键参数对内燃机汽车传动轴系扭振特性的影响，结果显示主副飞轮惯量比对扭振特性影响极大，而阻尼则几乎无影响。文献［5］中针对内燃机汽车传动轴系的扭振特性进行了鲁棒性分析，并进一步通过鲁棒优化实现了扭振特性及其鲁棒性的改善。

本研究以某款带有双质量飞轮的增程器轴系为对象，考虑双质量飞轮非线性特性，搭建轴系扭转动力学模型，结合试验进行模型验证，随后综合考虑确定优化参数、优化指标与约束条件，构建轴系扭振特性多目标多参数优化问题，采用第二代非支配排序遗传算法（NSGA—Ⅱ）进行优化求解，最后进行单参数扰动情况下的轴系扭振特性鲁棒性分析，评估系统的鲁棒性并对参数扰动的影响情况进行了分析。本研究的创新点主要在于对轴系采用多目标多参数优化方法，在应用中对轴系性能指标、设计边界约束与待优化参数进行较为全面的考虑，在鲁棒性分析中进行了对系统鲁棒性的评估与受参数扰动影响成因的分析。本研究较为贴近实际工程应用情况，为该类增程器轴系匹配与连接设计方案的评估与优化提供了参考案例，其方法和结果对工程实践具有一定的指导意义。

1 轴系扭转动力学模型构建

1.1 模型构建

采用系统仿真软件Amesim［6］对某款2.4GT 增程器轴系进行扭转动力学建模。Amesim 软件的特点为图形化建模，工作流明晰，且可调用的元件库众多。

该2.4GT 增程器带有一台直列4 缸2.4 L 增压汽油机。其轴系主要由减振皮带轮（torsional vibration damper，TVD）、曲轴连杆机构、双质量飞轮与ISG 电机轴及转子组成，如图1 所示。

图1 2.4GT 增程器的轴系机构简图

为便于计算，按集中参数法［7］对增程器轴系进行简化，并忽略零部件装配间隙对轴段间扭转刚度的影响，如电机轴花键与双质量飞轮花键槽的装配间隙对电机轴刚度的影响等；忽略由曲轴通过皮带驱动的各机构、附件（如凸轮轴、平衡轴、水泵与机油泵等）对轴系扭转振动的影响［8］；不考虑轴系弯曲振动与轴向振动对扭转振动的影响。以下将对轴系各部分建模过程进行说明。

所研究增程器轴系的减振皮带轮为橡胶式，主要包括带轮与轮毂，带轮与轮毂间以减振橡胶环连接。建模时将带轮与轮毂视作集中惯量，减振橡胶环处理为弹性元件，列出运动微分方程如式（1）所示。

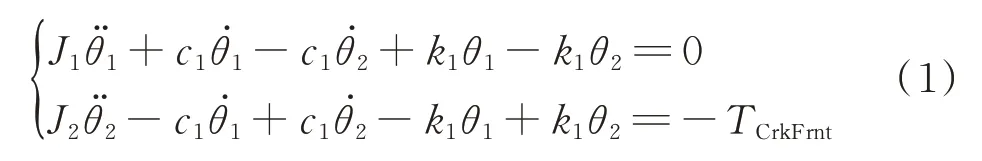
式中，θ1、θ2分别为带轮与轮毂角位移；J1、J2分别为带轮与轮毂的转动惯量；k1、c1分别为减振皮带轮的扭转刚度与阻尼；TCrkFrnt为曲轴前端传递扭矩。

减振皮带轮的阻尼为内阻尼，通过材料内部相互摩擦耗散振动能量。其阻尼值c按式（2）计算［9］。

式中，β为材料损耗因子，对于减振橡胶材料，一般范围为0.1～5.0，本文中取为0.2；ks为结构刚度；ω为振动圆频率，取为1 谐次激励圆频率。

曲轴连杆机构较复杂，将其划分为各曲拐单元与曲轴输出端等多个轴段。这些轴段简化为集中惯量节点，其中曲轴输出端惯量并入主飞轮惯量，各节点间以弹性元件连接。曲轴连杆机构的运动微分方程见式（3）。

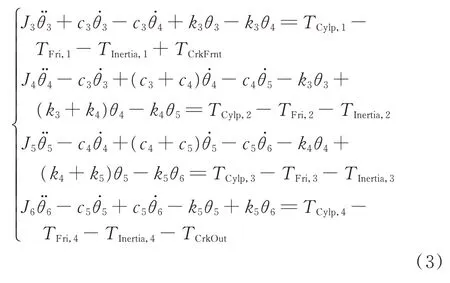
式中，θ3～θ6为各曲拐单元角位移；J3～J6为各曲拐单元等效转动惯量；k3～k5为曲轴轴段节点间等效扭转刚度；c3～c5为曲轴轴段间等效阻尼；TCylp，i、TFri，i、TInertia，i分 别为第i个曲 拐的气缸压力力矩、外阻尼摩擦力矩与往复惯性力矩，i=1，2，3，4；TCrkOut为曲轴输出端至主飞轮的传递扭矩。

各曲拐单元的等效转动惯量按动力学等效的原则进行计算，可参考文献［10］；各曲轴轴段间等效扭转刚度通过有限元分析得到；各轴段间等效阻尼为内阻尼，按式（2）计算，对于钢类材料，β一般取值范围为0.000 1～0.000 6，这里取0.000 3；各曲拐单元的气缸压力力矩、外阻尼摩擦力矩与往复惯性力矩计算详请参考文献［10］。

轴系的双质量飞轮为周向长弧形弹簧式，主要由主飞轮、副飞轮与长弧形减振弹簧组（包括提供双质量飞轮各阶扭转刚度的减振弹簧）组成。主飞轮与副飞轮处理为集中惯量，其运动微分方程见式（4）。

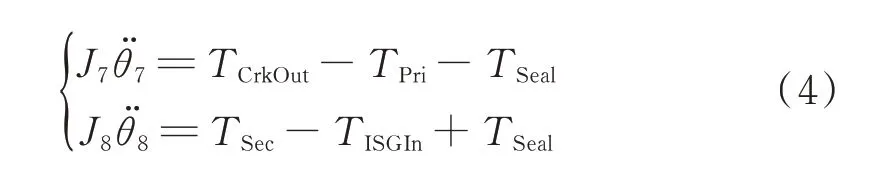
式中，J7、J8为主飞轮与副飞轮等效惯量；θ7、θ8分别为主飞轮与副飞轮角位移；TPri为主飞轮向减振弹簧传递的扭矩；TSec为减振弹簧向副飞轮传递的扭矩；TISGIn为副飞轮向电机轴及转子传递的扭矩；TSeal为主副飞轮接触面及密封垫圈间的摩擦力矩。

长弧形减振弹簧组是双质量飞轮的核心机构，它的运动状态影响双质量飞轮的扭转特性。由于这一类长弧形弹簧分布半径与质量相对较大，这与一般扭转减振器存在差异：（1）弹簧与壳体间因离心力产生的摩擦力不可忽略，导致弹簧在中高转速下呈现出一定的非线性［11］；（2）弹簧的转动惯量较大，不宜忽略。这两点差异可能对轴系固有特性产生影响，有必要搭建减振弹簧组的详细模型。将一个减振弹簧组等效为单个减振弹簧，并将其离散成多个质量单元，单元间以弹性元件（即子弹簧）连接。减振弹簧组模型如图2 所示，按此计算其运动状态。图2 中，φDMF为主副飞轮相对扭转角；φk为第k个质量单元与主飞轮中心线间的夹角，k=1，2，…，m，其中m为划分弹簧质量单元的数量；φ0为主飞轮与其中心线间的夹角；φm+1为副飞轮与主飞轮中心线间的夹角；FSprg，k为第k与第k+1个弹簧质量单元间传递力，按式（5）计算；Ff，k为第k个弹簧质量单元与主飞轮壳体间的摩擦力，按式（6）计算；FN，k为第k个弹簧质量单元所受支持力，按式（7）计算；F0为减振弹簧在双质量飞轮无扭转时的预载力，本研究中的弹簧在自然状态下存在空程，因而F0=0；弹簧刚度kSprg按主副飞轮相对扭转角计算，如式（8）所示；减振弹簧单元的运动微分方程见式（9）；最后由式（10）计算TPri、TSec。

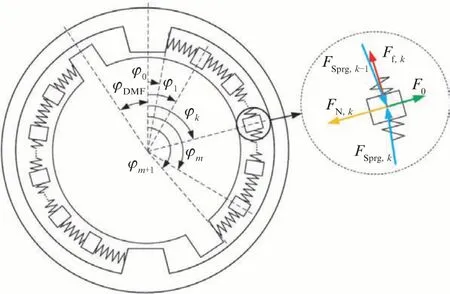
图2 双质量飞轮减振弹簧组模型

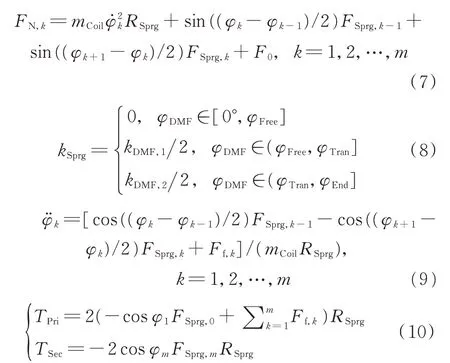
式中，m取6 以兼顾计算精度与速度［12］；σk为判断弹簧质量单元间是否传递力的函数，当k为0或m时可以参考文献［11］计算，当k为其他值时σk为1；kSprg为弹簧刚度；φ为减振弹簧自然状态下的分布角；cCoil为子弹簧阻尼；fStick，k、μVisc，k分别为第k个弹簧质量单元与主飞轮壳体的黏滞摩擦力与黏滑摩擦系数；kDMF，1、kDMF，2分别为双质量飞轮1阶与2阶刚度；φFree为弹簧空程角；φTran为弹簧刚度转变角；φEnd为弹簧压并角；mCoil为弹簧质量单元的质量，按弹簧组质量mSprg均布，有mCoil=mSprgm；RSprg为弹簧分布半径。

ISG 电机轴及转子简化为一个集中惯量，其与副飞轮间通过弹性元件连接，运动微分方程见式（11）。

式中，J9为电机轴及转子转动惯量；cISG为电机轴轴承阻尼；θ9为电机轴及转子的角位移；TISGOut为ISG电控单元为控制转速加载至电机轴端的扭矩。

各部件间的传递扭矩按照式（12）计算。

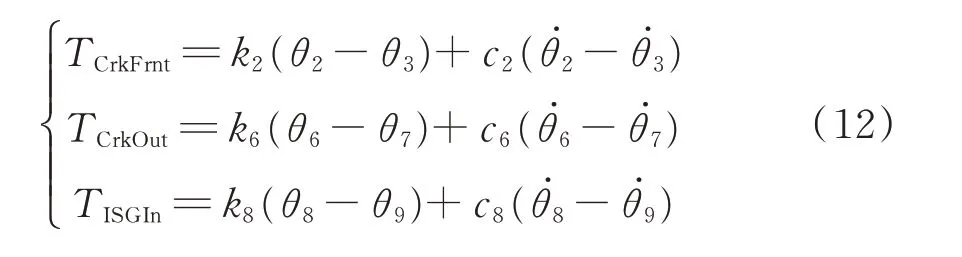
式中，k2为前端至第1 缸曲轴刚度；k6为第4 缸至输出端曲轴刚度；k8为电机轴刚度；c2、c6、c8分别为前端至第1 缸轴段阻尼、第4 缸至输出端轴段阻尼与电机轴段阻尼，均按式（2）计算，材料损耗因子取0.000 3。

各零部件理论模型确定后，在Amesim 中从元件库调用封装模型进行搭建，并确定模型所需参数。最终搭建的轴系扭转动力学模型如图3 所示。

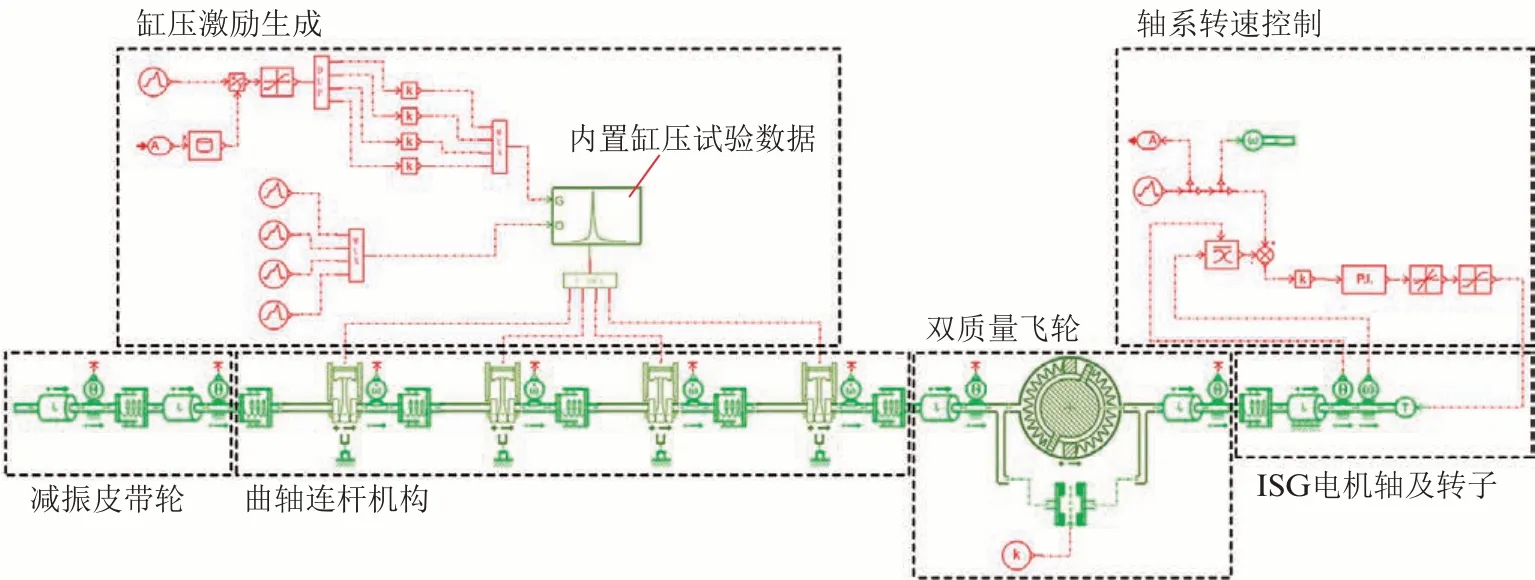
图3 轴系扭转动力学模型

图3 中，缸压激励生成模块根据增程器名义转速、转矩对曲轴连杆机构加载对应工况的缸压，轴系转速控制模块对ISG 电机轴及转子的转速进行比例积分（PI）控制。模型主要参数见表1。

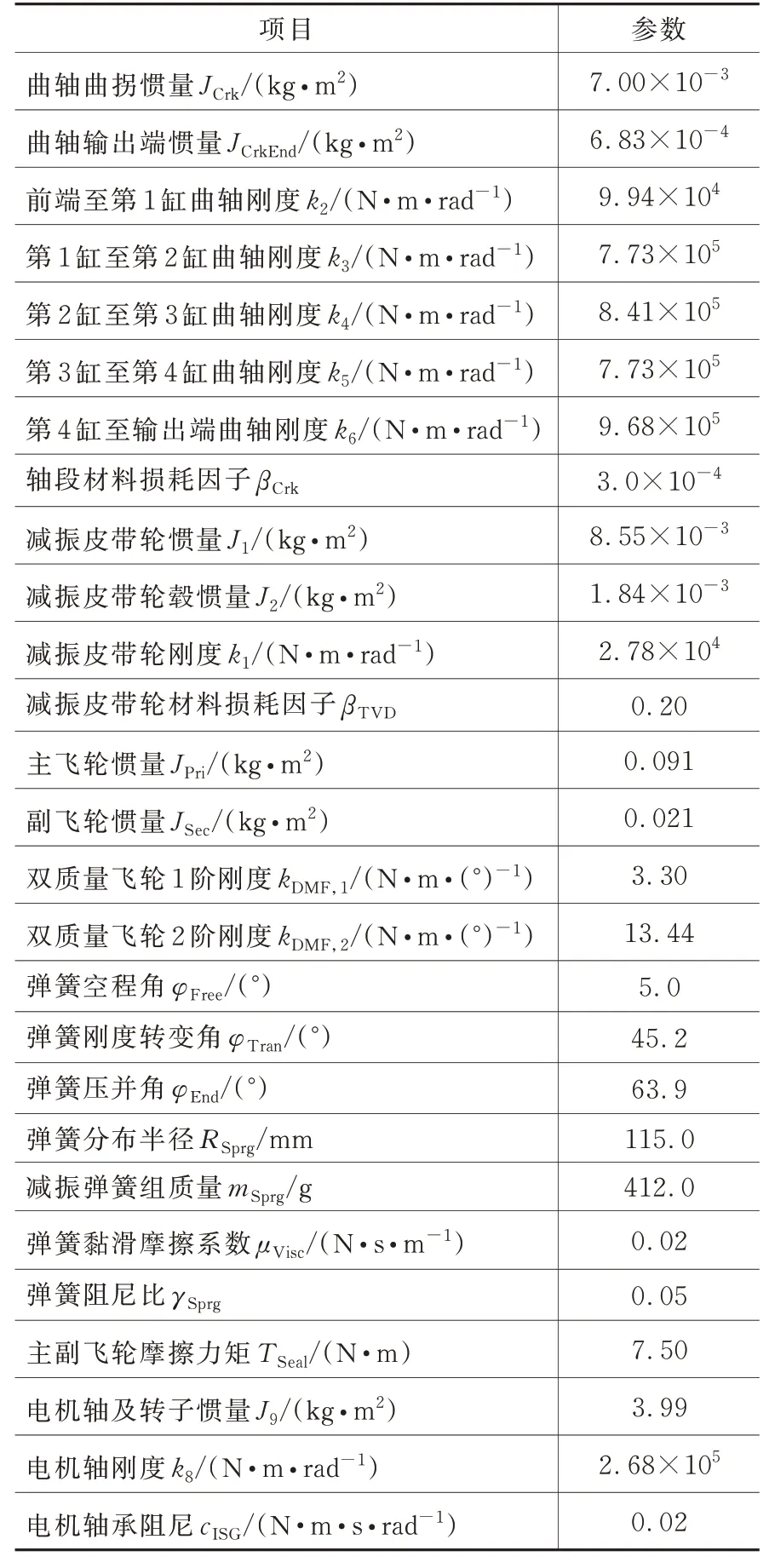
表1 2.4GT 增程器轴系的扭转动力学模型参数表

1.2 模型验证

相较于实际物理系统，所搭建的轴系扭转动力学模型基于集中参数法及相关假设进行了简化，该简化模型的准确性将影响到后续优化及鲁棒性分析的有效性，有必要对其进行验证。基于一款2.8DT增程器进行模型验证，这款增程器带有一台直列4缸2.8 L 的增压柴油机。该增程器轴系结构形式与2.4GT 增程器一致，且其双质量飞轮与2.4GT 增程器双质量飞轮为同一型号。因此，2.8DT 增程器与2.4GT 增程器的轴系扭振动力学模型机理一致，对2.8DT 增程器模型的验证结果也适用于2.4GT增程器，故而该验证是合理的。

增程器发动机自由端转速相对容易测量，故通过测量该处转速波动并与模型计算值进行对比来验证模型。试验原理图如图4 所示，在增程器发动机自由端（减振皮带轮毂处）安装光电编码器，测量轮毂处角位移与对应时间，经燃烧分析仪计算后传输至上位机储存。

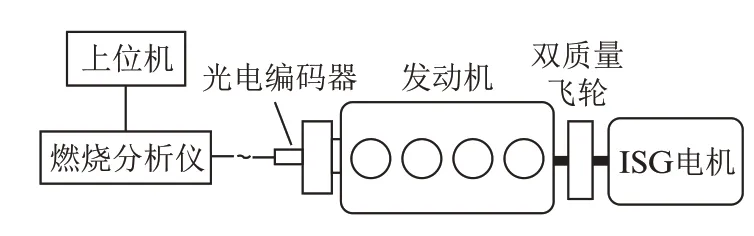
图4 试验原理图

增程器发动机自由端转速按式（13）计算。

式中，n为增程器发动机自由端转速，r/min；ΔθCA为光电编码器的测量间隔，（°）；ΔtCA为测量间隔对应的时间，s。试验所用光电编码器型号为AVL 365，其测量间隔为1°。

选取怠速工况（1 200 r/min、10 N·m），常用发电区域内不同转速低负荷发电工况（1 500 r/min 及2 500 r/min、50 N·m），常用最大发电工况（2 500 r/min、160 N·m）等多个增程器常见工况作为模型验证工况。计算所需的2.8DT 增程器轴系参数如表2 所示，验证工况的缸压如图5 所示。

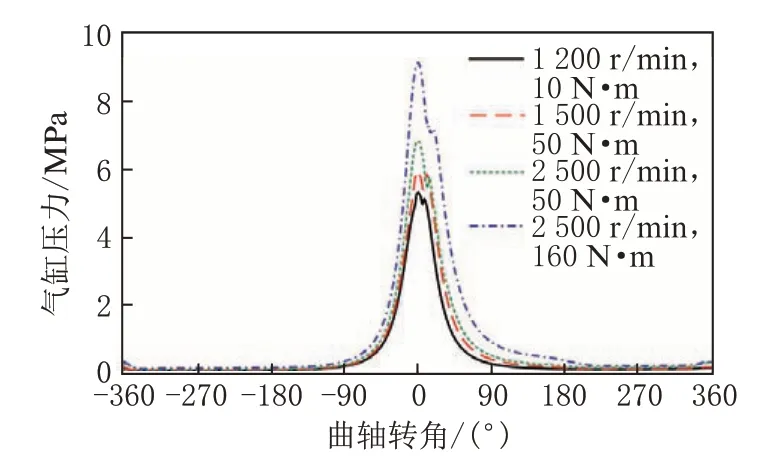
图5 2.8DT 增程器发动机在模型验证工况下的缸压

表2 2.8DT 增程器轴系的扭转动力学模型参数表

仿真与实测的各工况增程器发动机自由端转速波动对比如图6 所示。由图6 可见，搭建的轴系扭转动力学模型能较好地与实际情况吻合，可以用于下一步轴系扭振特性优化与鲁棒性分析。

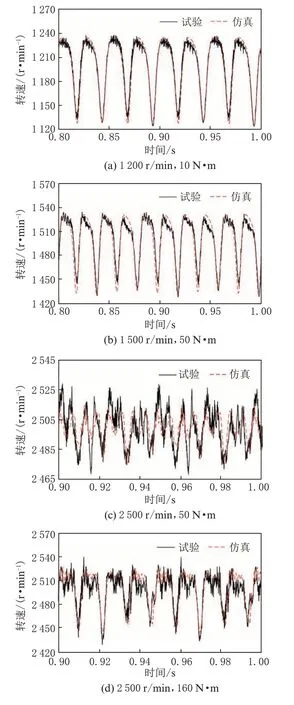
图6 试验与仿真的增程器发动机自由端转速波动对比

2 轴系扭振特性优化

2.1 多目标优化问题构建

为实现轴系扭振特性优化，首先需要明确能表征轴系扭振特性的评价指标，确定设计边界约束，选择待优化参数，以构建优化问题。

轴系扭振特性的首要评价指标是轴系的固有特性，本研究中取为低阶固有频率及模态阻尼比。低阶固有频率应当避开各工况的低阶主谐次激励频率，如果无法避开，则要求模态阻尼能大幅衰减模态共振。这些频域评价指标没有必要求其极大或极小值，故而将其处理为约束性评价指标，归入设计边界约束。

轴系的扭振响应也应当作为扭振特性的评价指标。选取怠速工况（1 200 r/min、20 N·m），常用发电工况（2 500 r/min、220 N·m），最大发电工况（3 000 r/min、320 N·m）等增程器典型稳态工况作为评价工况。选取减振皮带轮、主飞轮、副飞轮与电机轴及转子为轴系关键节点，分别代表增程器轴系自由端、连接处与扭矩传递终端。以关键节点的角加速度均方根及各轴段间传递扭矩峰谷值评判轴系的振动剧烈程度。轴系工作时，关键节点角加速度均方根越小，表征输入关键节点的能量波动越小；各轴段间传递扭矩峰谷值越小，表示各轴段所受交变扭矩幅值越小。

轴系的总转动惯量影响增程器瞬态响应速度，总惯量越小，增程器瞬态响应越迅速，因此也将其选为轴系扭振特性评价指标。

轴系设计的边界条件以保证轴系工作可靠性这一原则确定，主要考虑为：（1）各设计参数在物理上可行；（2）轴系固有特性应满足轴系在增程器各工况下不应有低阶主谐次激励激发的共振；（3）轴系在瞬时最大载荷下不会产生塑性变形，在持续交变载荷下不会发生疲劳失效，满足强度要求；（4）轴系的扭转变形不宜过大，以免影响轴上零部件正常工作，需要满足一定刚度要求；（5）双质量飞轮的各阶刚度提供的扭矩容量应当满足一定要求。

对于设计参数在物理上可行的约束，主要根据实际情况划定设计参数变动范围。对于轴系固有特性约束，低阶主谐次取为2～12 阶主谐次，要求1 阶固有频率低于增程器怠速转速下的2 谐次激励频率，2 阶固有频率高于增程器最高转速下12 谐次激励频率或系统2 阶模态阻尼能大幅衰减该模态共振，3 阶固有频率需要高于增程器最高转速下12 谐次激励频率。对于轴系强度约束，需要确定各轴段危险截面，按机械设计手册［13］计算疲劳与静强度安全系数，其中疲劳安全系数按无限寿命（107次载荷循环以上）计算。需要说明的是，安全系数与轴段材料、截面尺寸、工艺等具体参数相关，假定这些参数不随本研究关注的设计参数变化。轴系刚度约束则需要计算各节点间最大相对扭转角，不能超过一般传动轴的许用限值［13］。双质量飞轮的1 阶扭矩容量过大或过小可能导致双质量飞轮极限转角过大或过小，不利于具体参数设计。双质量飞轮总扭矩容量应在发动机最大扭矩基础上保有一定储备扭矩［14］。

由表1 可见，增程器轴系设计参数众多，需要从中筛选出对轴系扭振特性影响较大的参数。根据划定的参数变动范围，在增程器典型稳态工况下进行了单参数影响分析以选取待优化参数。

通过单参数影响分析发现，主飞轮惯量是减振弹簧前端节点角加速度与传递扭矩的主影响参数。电机轴及转子惯量为减振弹簧后端节点角加速度与传递扭矩的主影响参数。减振皮带轮材料损耗因子与主副飞轮摩擦力矩分别对减振皮带轮角加速度与副飞轮角加速度有较大影响。而对于频域特性，1 阶模态以减振弹簧前端各节点为主振动节点，主要受主、副飞轮惯量及双质量飞轮扭转刚度影响；2 阶模态以减振皮带轮为主振动节点，主要受减振皮带轮惯量、刚度、阻尼及前端至第1 缸曲轴刚度影响；3 阶模态以副飞轮为主振动节点，主要受减振弹簧后端惯量、刚度影响。

以上对轴系扭振特性影响较大的设计参数被选为待优化参数，如表3 所示。

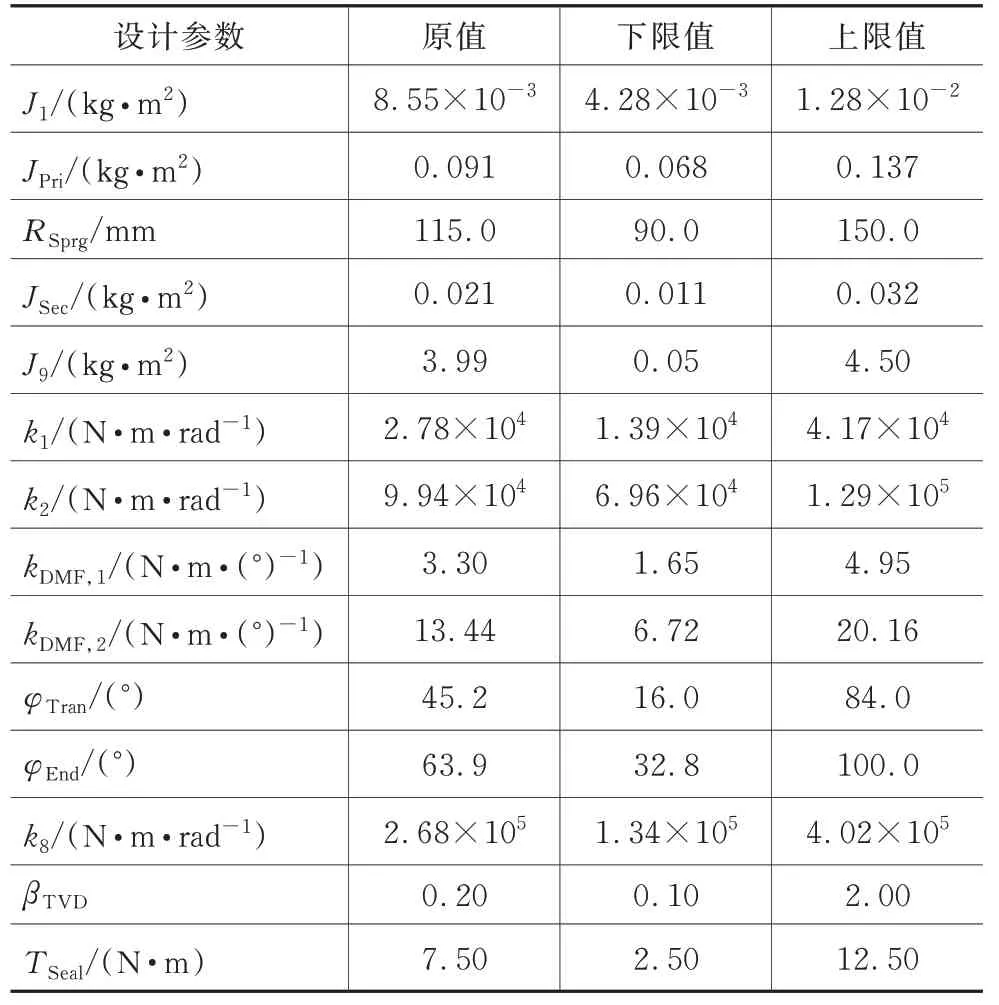
表3 待优化参数及其变动范围

在确定轴系扭振特性评价指标、设计边界条件与待优化参数后，构建优化问题，其中式（14）为优化参数表达式，式（15）为目标函数表达式，式（16）为约束条件表达式。

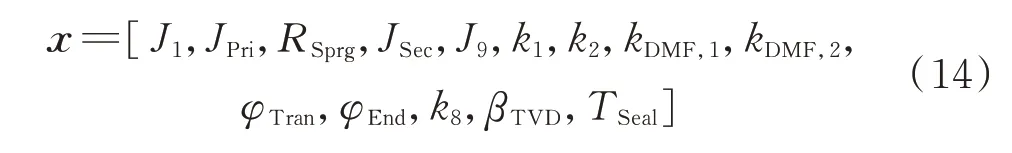
式中，x即为优化参数；aTVD，i（x）、aPri，i（x）、aSec，i（x）、aISG，i（x）（i=1，2，3）分别为减振皮带轮、主飞轮、副飞轮与ISG 电机轴及转子等关键节点在怠速、常用发电与最大发电工况下的角加速度均方根值；F1(x)～F4(x) 分别为4 个关键节点角加速度均方根值在3 个典型稳态工况下的加权值；α1、α2、α3为这3个工况的权重，分别取为0.10、0.75、0.15；Ti，1(x)，Ti，2(x)，Ti，3(x)分别为怠速、常用发电与最大发电工况下轴系第i与i+1 节点间传递扭矩的峰谷值，i=1，2，3，4，5，6，8；F5(x)为各节点间传递扭矩峰谷值之和；F6(x)为轴系总惯量；x0为轴系原设计参数，各目标函数均以x0计算的评价指标为基准值进行了归一化；xi与x0，i分别为x与x0中第i个元素，i=1，2，…，14；xL、xH为优化参数x变动的下限与上限；fi，1(x)、fi，2(x)、fi，3(x)分别为增程器在怠速、常用发电与最大发电工况下轴系的第i阶固有频率，i=1，2，3；γ2，2(x)、γ2，3(x)为常用发电工况与最大发电工况下的轴系2 阶模态阻尼比；Sτ，i(x)、Ssτ，i(x)分别为轴系第i与i+1 节点间轴段危险截面的扭转疲劳强度安全系数与静强度安全系数，i=2，3，4，5，6，8；Scτ，i(x)为第i段子弹簧的疲劳强度安全系数，i=1，2，…，7；[θi]为第i与i+1 节点间轴段许用扭转角，i=2，3，4，5，6，8。需要说明的是，由于增程器轴系扭振系统存在非线性，因此在不同工况下轴系固有特性存在差别。

2.2 优化问题求解与结果分析

本研究构建的轴系扭振特性优化问题是一个多目标带约束的非线性优化问题，选用第二代非支配排序遗传算法（NSGA—Ⅱ）求解该问题，这一算法适用于复杂函数的多目标全局优化问题。算法流程如图7 所示，根据个体间是否互相支配进行非支配度排序，评价个体优劣程度，对种群进行交叉、变异与筛选，改进个体的适应度，最终获得一组接近全局最优的非支配解集，即 Pareto解集［15］。

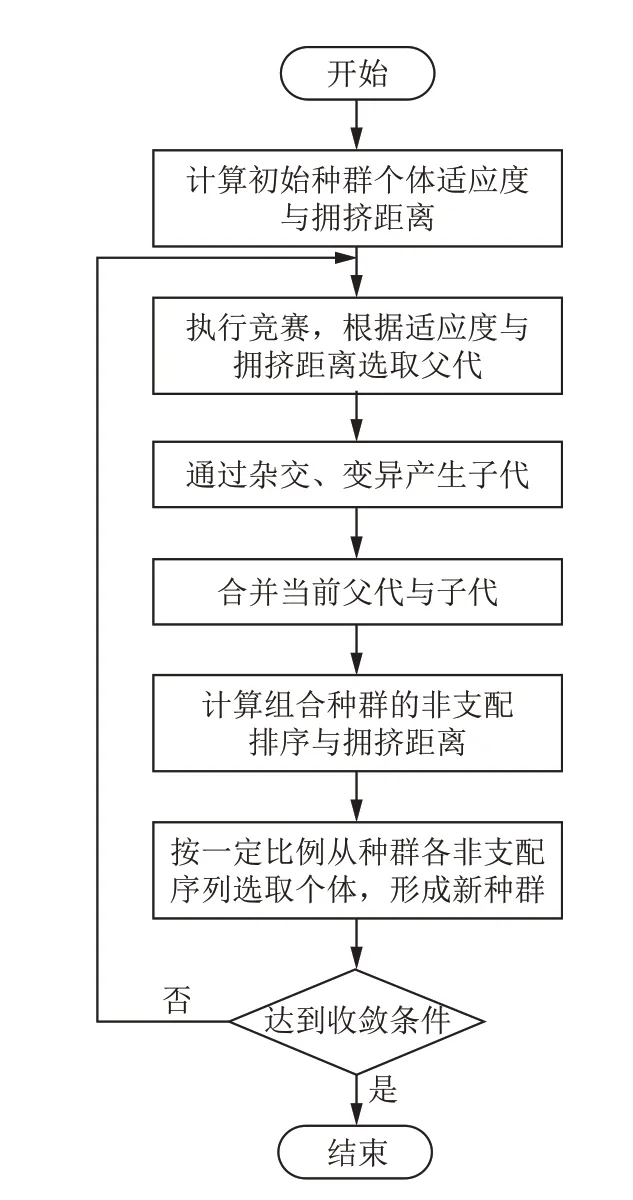
图7 NSGA—Ⅱ算法流程图

MATLAB 优化工具箱中已经集成了NSGA—Ⅱ算法，可以直接调用。基于此进行MATLABAmesim 联合仿真优化，其流程如下：（1）在MATLAB 中生成种群，随后将种群对应的参数组写入Amesim 的参数文件；（2）调用Amesim 编译生成的可执行文件，计算轴系在典型工况下的扭振时域响应与频率特性；（3）在MATLAB 中读取Amesim 仿真生成的结果文件，计算各目标函数值与约束条件满足性；（4）在MATLAB 中根据计算结果进行种群进化；（5）重复步骤（1）～步骤（4），直至算法收敛。当Pareto 前沿面随着种群进化基本无变化同时前沿面上的解足够分散时，则可以认为算法收敛。具体收敛条件详请参阅文献［16］。

算法参数设置如表4 所示。在种群进化至288代时算法收敛，可以认为最后一代在Pareto 前沿面上的解为Pareto 解集。

表4 NSGA—Ⅱ算法参数设置

为了从Pareto 解集中选出最优解，构造了如式（17）所示的综合评价函数，这一函数是各目标函数至其在解集中最小值相对距离的加权平方和，该值越小表明解对应的各目标函数综合越优。

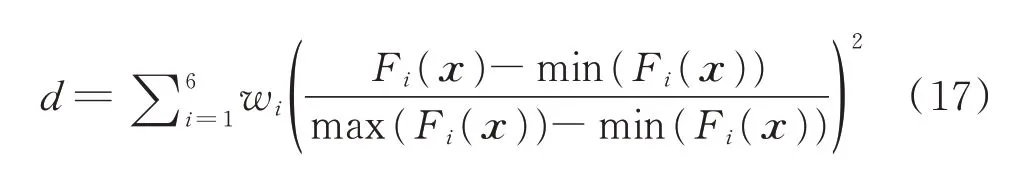
式中，wi为各目标函数与其最小值间相对距离的权重，分别取为1.0、1.0、0.8、0.1、1.0、3.0。最终选定的优化参数与原设计参数对比如表5 所示，优化前后评价指标及部分约束指标对比如表6 所示。优化结果表明，除电机轴及转子角加速度与节点间传递扭矩之和略有增大外，其余评价指标均有减小，满足了规定的约束条件，弹簧疲劳安全系数与双质量飞轮总扭矩容量达到要求，轴系低阶固有特性也得到改善。这表明对轴系扭振特性的优化是有效的。对各参数依次优化则难以同时满足各项约束，也难以保证最终优化结果综合最优，故而本研究中的多目标多参数优化方法具有一定优势。

表5 优化前后设计参数对比

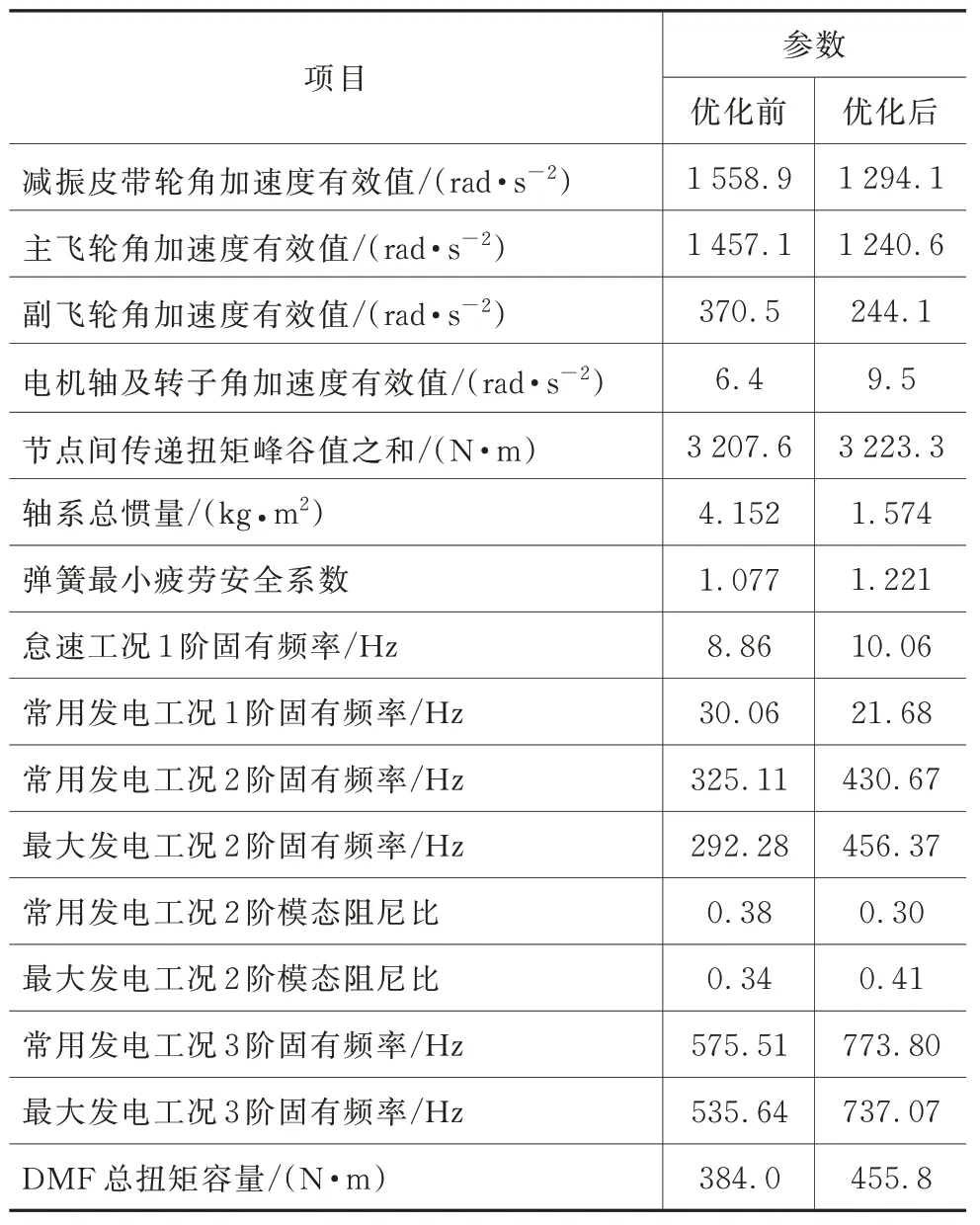
表6 优化前后评价指标及部分约束指标对比

3 轴系扭振特性的鲁棒性分析

3.1 鲁棒性分析方法

前文中对轴系扭振特性的优化基于确定的参数值进行，而在实际生产制造乃至运行中，增程器轴系受某些扰动参数的影响，使评价指标不同程度地偏离设计预期，为此有必要进行轴系扭振特性的鲁棒性分析。

首先，需要构建鲁棒性分析方法。

扰动参数是一组随机变量，它们服从一定的分布规律，系统评价指标是这些随机变量的函数，也存在某种分布规律。鲁棒性分析即分析参数扰动对指标分布的影响及其成因［17］。

假设各扰动参数不相关，且都服从正态分布，即e～N(μ，σ2)，均值μ取为扰动参数的确定值edet，标准差σ按式（18）计算。

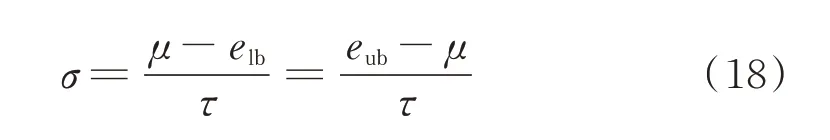
式中，eub、elb为参数扰动的上下限；τ为σ水平，本研究中取为2，即扰动参数值落在扰动上下限范围内的概率为95%。

轴系扭振特性指标与轴系设计参数函数关系复杂，采用蒙特卡洛法对轴系扭振特性指标的概率分布进行数值计算，得到指标的频次分布。为保证计算结果足够接近于概率分布，样本容量选为1 200 组。

选择轴系扭振特性评价指标的变异系数ξ作为系统鲁棒性的评价指标，如式（19）所示。

该指标反映了各个扭振特性评价指标分布的离散程度，评价指标分布越离散表明系统越容易受参数扰动影响。对于约束性评价指标（即轴系低阶固有频率），应主要考虑其满足约束的程度，满足评价指标约束的轴系不会产生严重共振，为此要求约束性评价指标不满足约束条件的概率不大于5%。

3.2 单参数扰动情况下的系统鲁棒性分析

本研究中考虑的扰动参数包括表5 中优化的设计参数与发动机激励，发动机激励扰动分为缸压幅值波动系数kCylp与缸压曲线相位φCylp的扰动。按工程经验确定各扰动参数的扰动范围：惯量的扰动范围为确定值±5% 内，刚度与阻尼的扰动范围为确定值±10% 内，弹簧刚度转变角与弹簧压并角扰动范围为确定值±3°内，缸压幅值波动系数扰动范围为［0.95，1.05］，缸压曲线相位扰动范围为［-1.5°，1.5°］。

假定各扰动参数单独作用于轴系系统，以常用发电工况为例，分析各参数扰动对轴系扭振特性的影响。根据选定的鲁棒性评价指标，发现副飞轮角加速度、电机轴及转子角加速度与轴系低阶固有频率等指标容易受扰动参数影响，以下将对这些指标受参数扰动的影响进行分析。超出变动范围的扰动参数是物理上不可行的，因此在结果中剔除了这些样本。

图8 展示了轴系2 阶模态阻尼比受减振皮带轮设计参数扰动的影响情况。可见2 阶模态阻尼比有一定概率小于设计允许下限值（0.30），这削弱了增程器轴系对该模态共振的抑制作用。

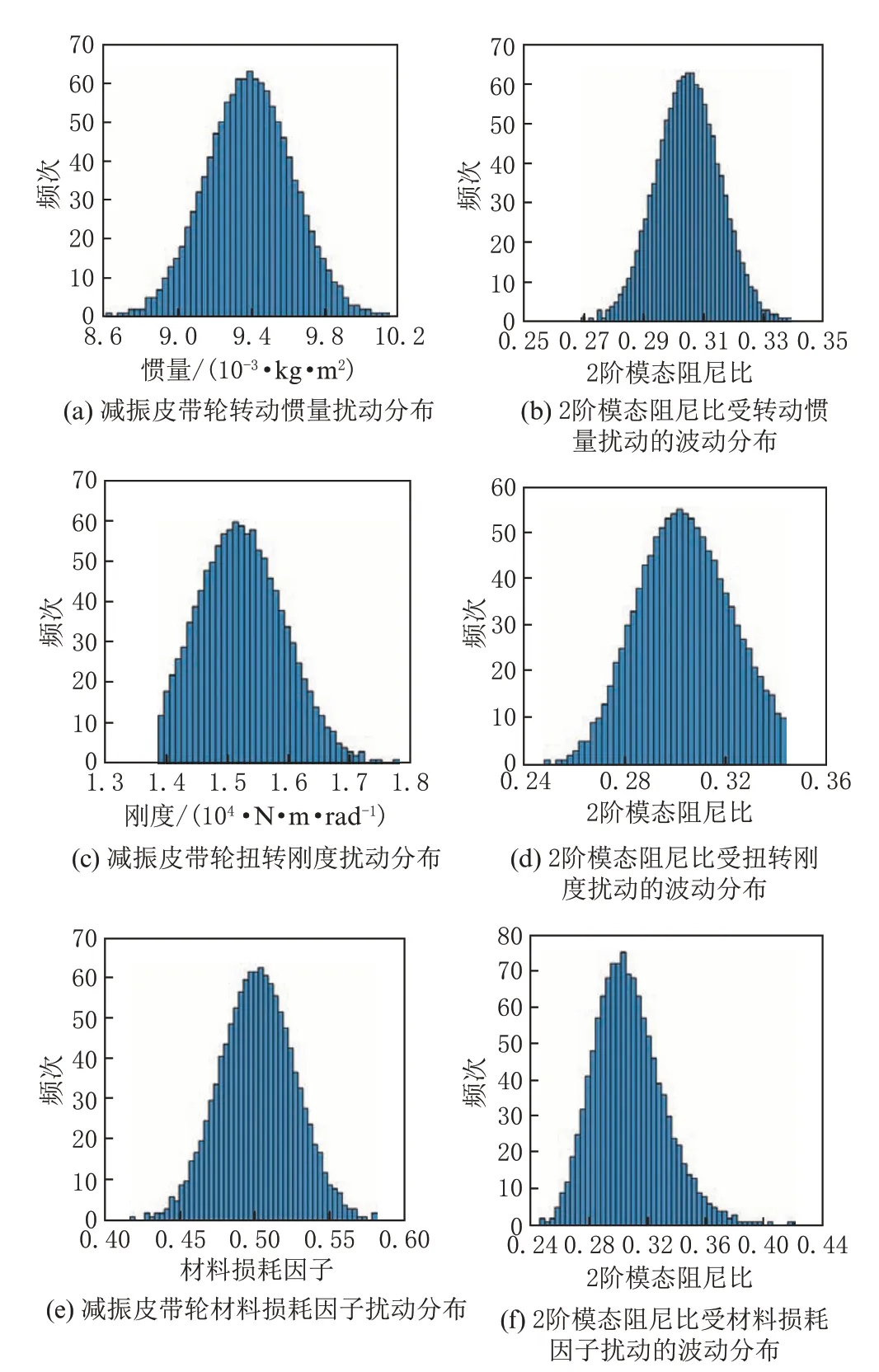
图8 2 阶模态阻尼比受减振皮带轮扰动参数影响情况

在双质量飞轮2 阶刚度参数扰动下，其主影响指标波动分布情况如图9 所示，副飞轮与电机轴及转子的角加速度受该参数扰动影响较大。对于副飞轮，其角加速度的18 谐次分量占主导地位，这一谐次激励频率（750 Hz）与3 阶固有频率（775 Hz）相近，推测为共振谐次；对于电机轴及转子，其角加速度的2 谐次占主导地位。可见双质量飞轮2 阶刚度的扰动影响了发动机激励至副飞轮与电机轴及转子的传递特性。1 阶固有频率虽然受双质量飞轮2 阶刚度扰动影响较大，但并未超出设计上限值（30 Hz）。

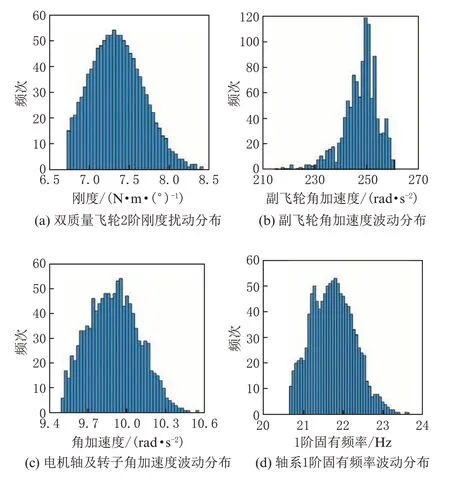
图9 双质量飞轮2 阶刚度扰动及其主要影响指标分布

图10 展示了主副飞轮摩擦力矩的扰动分布与副飞轮角加速度的波动分布。由图10 可见两者分布相似，这表明在扰动范围附近副飞轮角加速度随主副飞轮摩擦力矩近似线性变化。

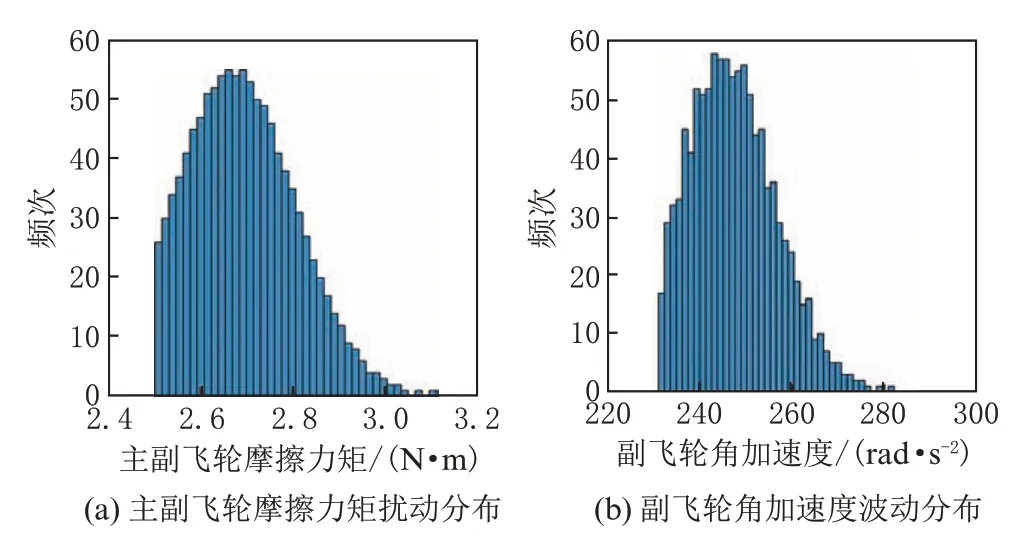
图10 主副飞轮摩擦力矩扰动对副飞轮角加速度影响

副飞轮角加速度分别受副飞轮惯量及电机轴刚度参数扰动的影响情况与其成因见图11 与图12。轴系3 阶固有频率对这2 个设计参数较敏感，在扰动范围内，副飞轮角加速度存在18 谐次激励频率与3 阶固有频率相交产生的共振峰，故而扰动参数分布映射的副飞轮角加速度分布较离散，且异于正态分布。

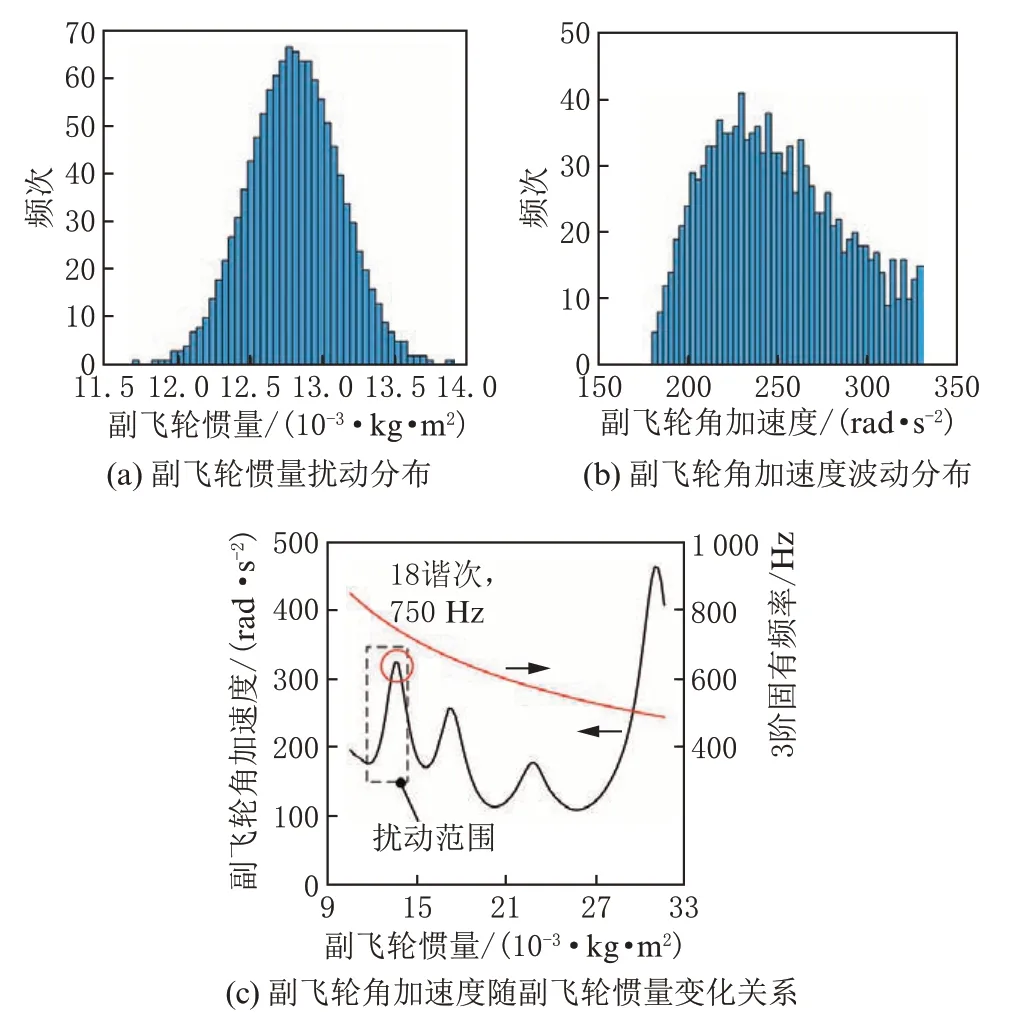
图11 副飞轮惯量扰动分布对副飞轮角加速度波动的影响

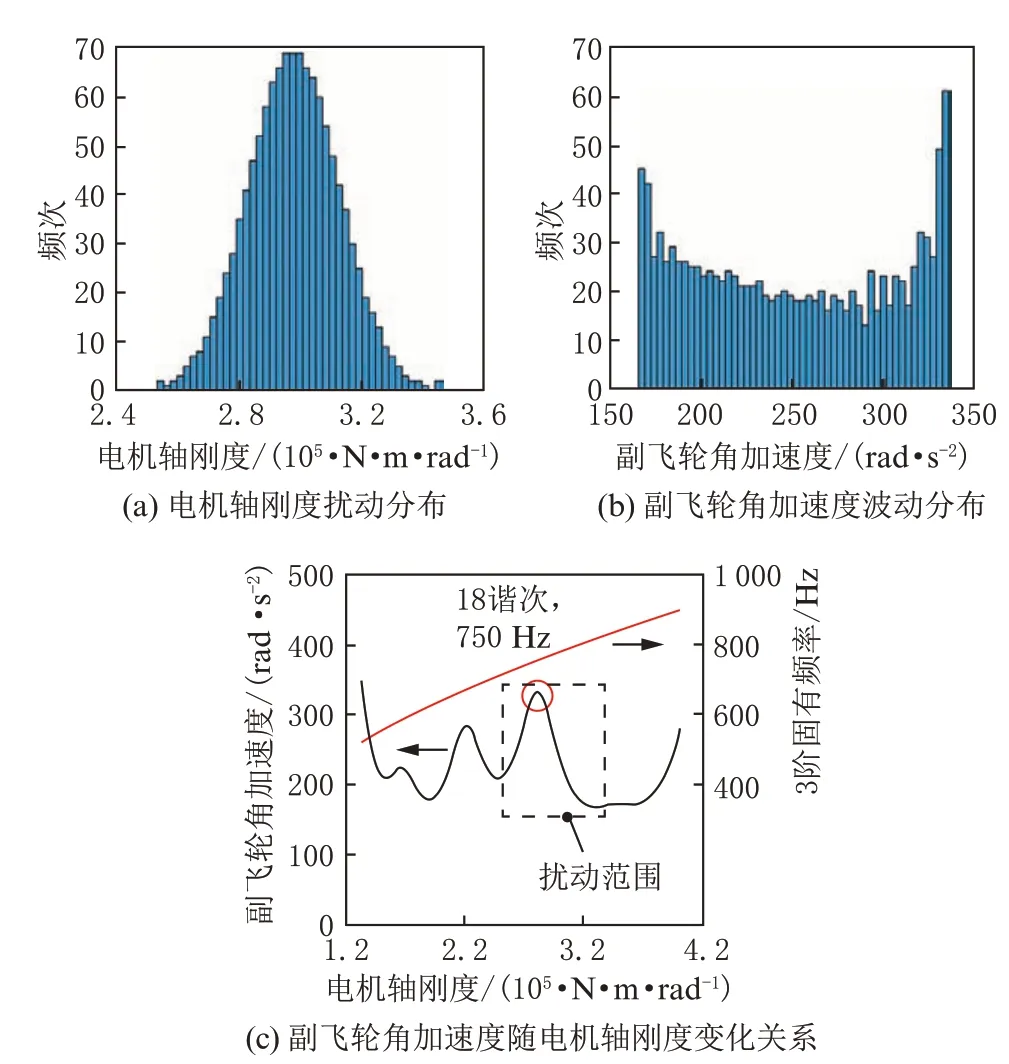
图12 电机轴刚度扰动分布对副飞轮角加速度波动的影响

以第1 缸为例，缸压幅值系数与缸压曲线相位扰动对副飞轮角加速度影响如图13 所示。单缸压力变动会导致发动机部分谐次的激励力矩不完全平衡，此外也会影响原本无法平衡的主共振谐次激励力矩幅值，进而影响角加速度共振峰值，这两个因素综合作用导致副飞轮节点产生相对较大的角加速度波动。

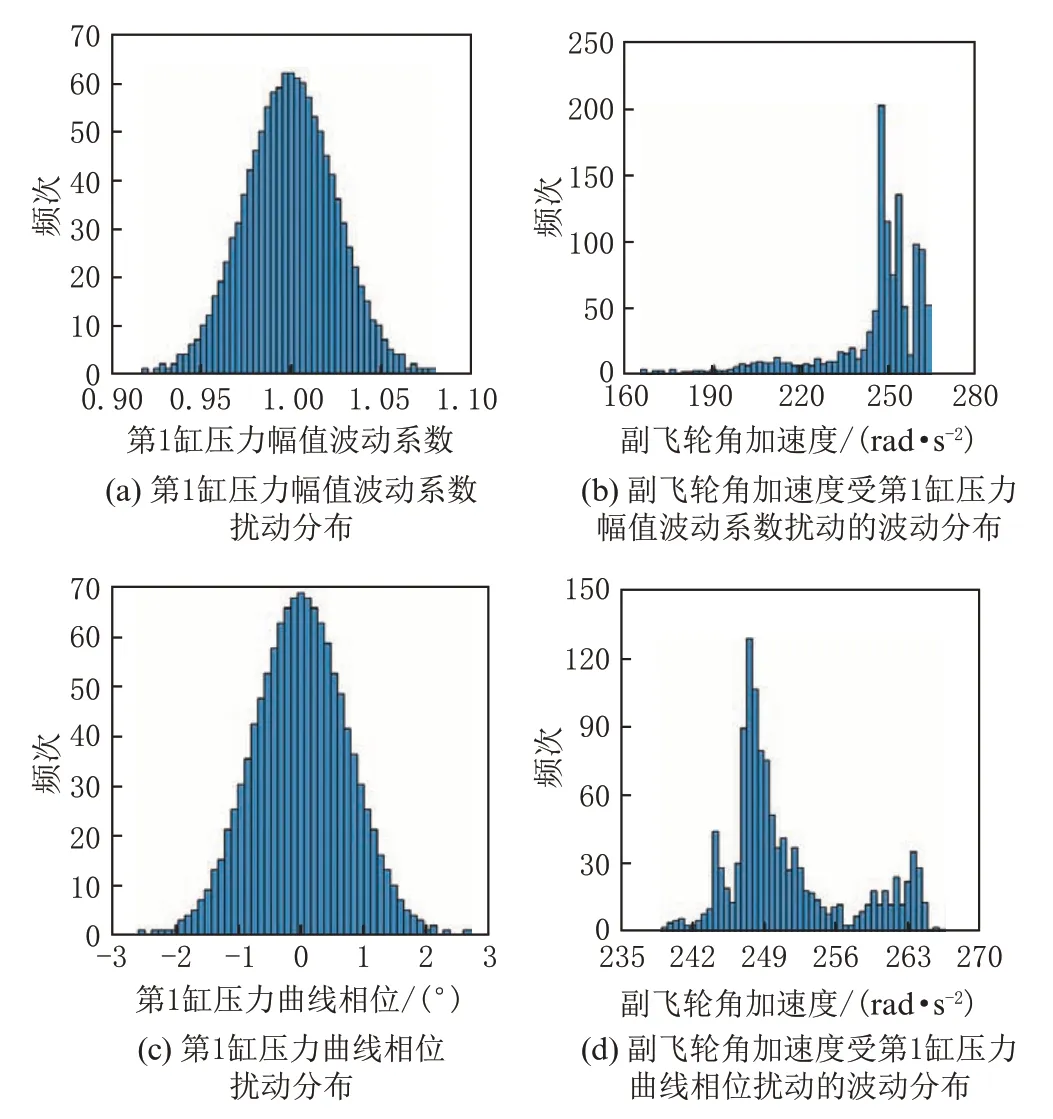
图13 副飞轮角加速度受激励扰动参数影响情况

对轴系的鲁棒性分析表明，轴系低阶固有特性虽然受双质量飞轮2 阶刚度，减振皮带轮惯量、刚度、阻尼，副飞轮惯量及电机轴刚度等设计参数扰动的影响较大，除2 阶模态阻尼比外其余参数均满足设计边界的概率约束。关键节点中副飞轮与电机轴及转子角加速度受参数扰动影响相对较大，分布相对离散，但是波动范围的绝对值较小，这得益于双质量飞轮的减振特性。减振弹簧后端的扭转振动大幅衰减，同时轴系的3 阶模态共振也不严重，可以认为这两个扭振特性指标具有一定的鲁棒性。减振皮带轮刚度、双质量飞轮2 阶刚度与主副飞轮摩擦力矩等设计参数扰动分布有一定概率超出约束范围，这是因为本研究中在扭振特性多目标优化阶段未考虑设计参数的扰动，部分优化后的参数确定值靠近设定的参数变动边界。而在扭振特性鲁棒性分析阶段考虑了设计参数扰动，并以参数确定值为扰动分布均值，说明参数确定值还应当考虑参数扰动的影响进行选取，这还需要进一步研究。以上分析结果在基于参数确定值的分析及优化过程中难以得到，可见对轴系扭振特性进行鲁棒性分析是有必要的。

4 结论

（1）在Amesim 中搭建的考虑双质量飞轮非线性特性的增程器轴系扭转动力学模型能较好地与试验结果吻合。

（2）对轴系的多目标多参数优化结果表明，轴系大部分扭振特性获得改善，满足了轴系强度与刚度要求，同时轴系固有特性得到改善。

（3）对轴系扭振特性进行的鲁棒性分析结果表明：减振皮带轮与主飞轮角加速度指标鲁棒性较好；副飞轮与电机轴及转子角加速度易受激励幅值相位、副飞轮惯量、电机轴刚度、双质量飞轮2 阶刚度与主副飞轮摩擦力矩等参数扰动影响，但两指标波动范围绝对值较小，因而也认为其具有一定鲁棒性；2 阶模态阻尼比受减振皮带轮设计参数影响，有一定概率超出许用范围，需要继续优化；减振皮带轮刚度、双质量飞轮2 阶刚度及主副飞轮摩擦力矩等设计参数的扰动有一定概率超出许用范围，尚待进一步研究。