集体自动落纱装置设计与拓扑优化研究

郑 杰，高贵军，杨文强，王唯博

(1.太原理工大学 机械与运载工程学院，山西 太原 030024； 2.山西省矿山流体控制工程技术研究中心，山西 太原 030024；3.矿山流体控制国家地方联合工程实验室，山西 太原 030024 )

目前国内拥有粗纱纺机30 000台以上，纺织能力达到1.2亿锭，绝大多数纺织机(98%以上)采用人工落纱，没有自动落纱设备，每个满纱管质量大约2.5 kg，每台车一般为200个纱管，工人需要不停地取下粗纱管和放入空管，这是一个工作强度大、落纱效率低的岗位[1]。随着目前企业“用工荒”的出现，人员工资成本的增加，落纱的问题已经严重制约了纺织行业的发展，自动落纱代替人工落纱成为纺织行业的趋势。

为降低工作强度和提高落纱效率，研究人员设计了各种自动落纱装置。张钊等[2]设计了一种自动落纱机自适应纱管夹持器，能够实现稳定可靠地落纱操作。贾军政[3]设计一种全新的智能落纱机，实现了拔满纱管、插空管过程自动化。张凡等[4]采用仿生学手指结构及抓取原理,设计优化一种自动落纱机械手实现多尺寸落纱。毕丽蕴等[5]设计了一种全新的粗纱机自动落纱机器人，该自动落纱机器人与已装机运行的粗纱机配套使用实现自动落纱。上述研究中的落纱方式单次抓取纱管数量有限，机械手运动稳定性直接影响抓取效率，而且机械手抓取对纱管会造成损坏。

本文研究基于对粗纱机纺纱工艺的充分认识，对传统粗纱机进行改造，使得下龙筋可以脱离粗纱机机架，设计了一种集体自动落纱装置。该装置在不改变粗纱机基本结构的前提下，与粗纱机配套使用，不仅降低人工劳动强度，还大大提高落纱效率，避免纱管损坏，具有广阔的市场应用前景。装置的稳定性好坏直接影响落纱工作正常进行，因此研究此装置的动态特性显得尤为重要。

1 集体自动落纱装置设计

1.1 设计原则

集体自动落纱装置需要满足一些设计原则，主要有以下几个方面[6]：①满足振动稳定性。落纱工作的正常进行取决于此装置的稳定性好坏。②满足结构工艺性。设计合理，便于制造，而且结构强度、刚度满足要求。③满足一定的定位精度。空满管交换需要一定的精确度要求才可实现。

1.2 工艺方案设计

粗纱机一轮纺纱结束后，下龙筋脱离粗纱机机架[7]，和满纱管一同沿气动滑台水平移出，到达指定位置后限位开关控制使其停止，同时步进电动机启动带动丝杠，进而带动托板托着下龙筋和满纱管上升，到达指定位置后停止，同时开始空满管交换，交换完成后，满纱管通过导轨运输到所需要的细纱机上，空管和下龙筋则由托板托着下降，直到回到粗纱机后下龙筋复位，进行下一轮的纺纱。在各个机构的协同作用下，一轮落纱工作结束。具体工艺流程如图1所示。

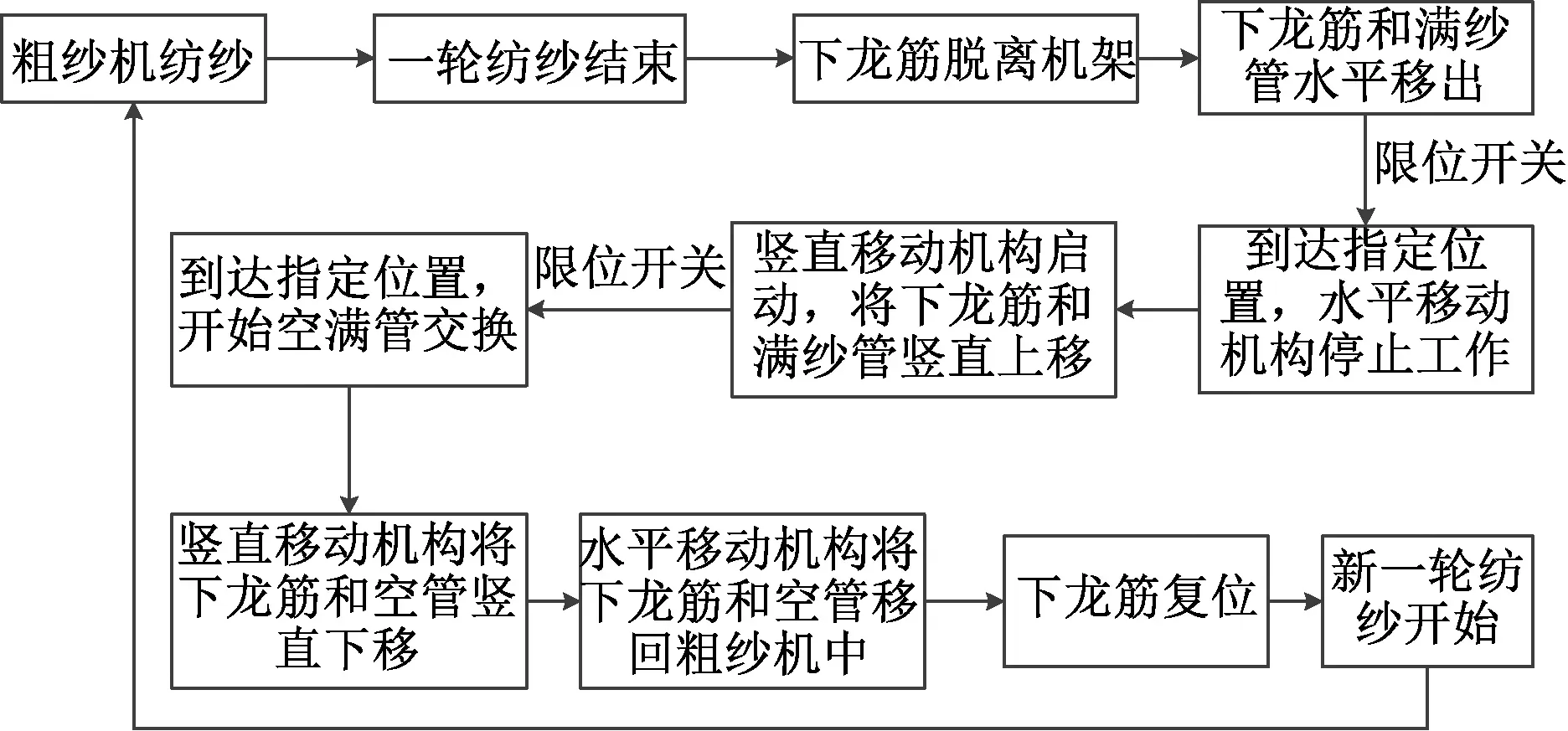
图1 自动落纱装置的工艺流程图Fig.1 Process flow diagram of automatic doffing device

1.3 总体设计方案

对传统粗纱机进行改造，设计了一种集体自动落纱装置，可以与不同型号的粗纱机配套使用。总体设计方案装置其中一节如图2所示，具体设置落纱装置的节数由不同型号粗纱机的锭数来确定。此装置包括水平移动机构、竖直移动机构以及粗细联输送机构。水平移动机构是通过气动滑台带动下龙筋和纱管实现水平运动；竖直移动机构可以将下龙筋和纱管竖直平滑运送；粗细联输送机构可以实现空满管交换以及输送纱管。

图2 总体设计方案Fig.2 Overall design scheme

2 集体自动落纱装置的主要机构设计

2.1 水平移动机构

为使脱离的下龙筋和满纱管移出机架实现自动落纱，设计水平移动机构如图3所示，包括气动滑台、龙筋配合块和限位开关等。龙筋配合块与下龙筋间隙配合，固定在气动滑台的滑块上，一同水平移动，触发到限位开关后停止，同时启动竖直移动机构。

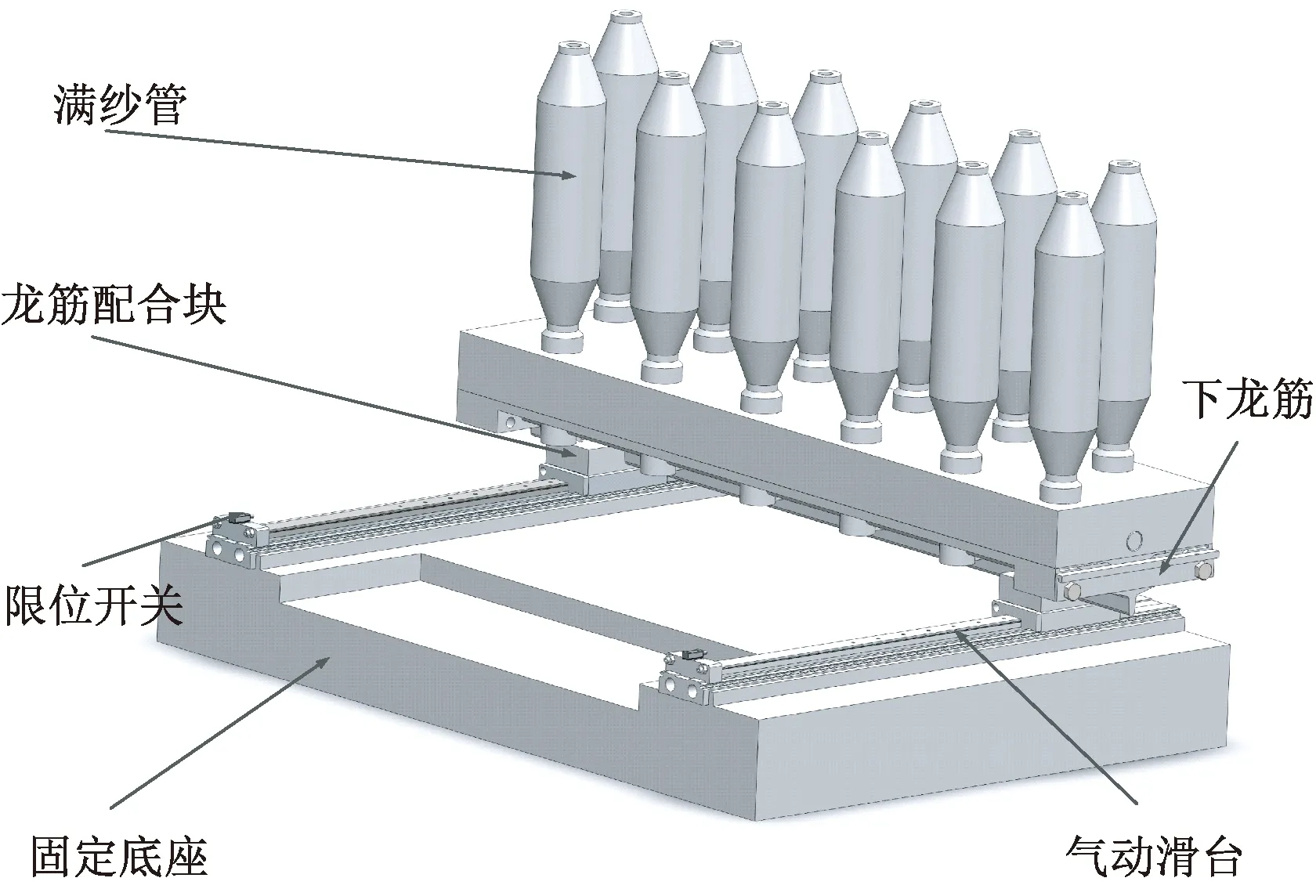
图3 水平移动机构Fig.3 Horizontal moving mechanism

2.2 竖直移动机构

为将水平移出的满纱管与上方导轨中的空管实现空满管交换，设计竖直移动机构如图4所示，包括步进电动机、丝杠、托板、导杆、直线轴承、上固定板和下固定板等。

图4 竖直移动机构Fig.4 Vertical moving mechanism

2台步进电动机各有自己的从控制器，主控制器向从控制器同时发出脉冲信号，同时编码器时刻检测2台电动机转速，使转速误差维持在合理的范围，从而实现2台电动机的同步传动。

步进电动机启动带动丝杠转动，进而带动托板托着下龙筋和满纱管竖直移动，触发到限位开关后停止，同时粗细联输送机构启动，双方协同配合下完成空满管交换。

2.3 粗细联输送机构

输送纱管是落纱工作的最后一步，为实现空满管交换和输送纱管，设计了粗细联输送机构，包括导槽、行走机构、吊锭等。粗细联输送机构如图5所示，导槽固定在机架上，行走机构在导槽中运动。空满管交换完成后，满纱管随行走机构运输到所需要的细纱机上，空管在下龙筋上随着托板竖直下降，直到回到粗纱机进行新一轮的纺纱。

图5 粗细联输送机构Fig.5 Combined conveying mechanism of roving frame and spinning frame

3 落纱架的模态分析

落纱架是竖直移动机构的关键部位，其稳定性对落纱工作有重要的影响，有必要对其进行分析。落纱架中的托板是板焊接式结构，各连接处有倒角、螺纹孔，为了加快分析速度和提高网格质量，需要对其进行合理简化，省略倒角、螺纹孔这些对动态特性影响小的结构[8]。简化后的落纱架模型如图6所示，表1为各部件的材料属性。

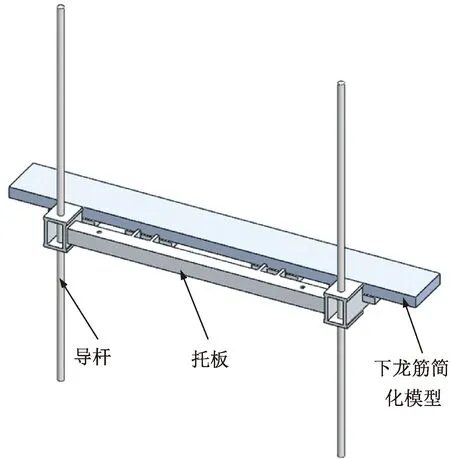
图6 落纱架简化模型Fig.6 Simplified model of doffing frame

表1 各部件的材料属性Tab.1 Material properties of each component

由于落纱架各个组件结构存在差异，采用以六面体、楔形和四面体结合的方式，分别对各个组件进行网格划分，落纱架网格划分图如图7所示，整体共有28 132个节点，18 462 个单元。

图7 落纱架网格划分图Fig.7 Grid division diagram of doffing frame

相互作用和边界条件设定：整体设置通用接触；下龙筋在托板上，随托板同时升降，二者之间保持相对静止，因此设为绑定约束；导杆上下端完全固定；托板升降只有Y方向一个平移自由度，其他自由度均被限制。

3.1 模态分析理论

模态分析主要用于确定系统自身的共振频率和振型，同时是后续谐响应分析的基础。

将系统离散成有限个节点和单元后，得到的振动微分方程[9]见式(1)：

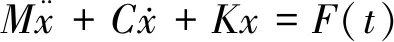
(1)

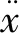
系统的固有特性只与自身属性有关，故F(t)=0，从而得到无阻尼C=0自由振动的微分方程见式(2)：

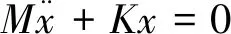
(2)

设系统的响应：

x=αsin(ωit+φ)

(3)

式(3)中：α为系统的n阶振型向量；ω为系统的各阶自然圆频率，Hz；φ为系统的振动初相位；t为系统的时间，s。

将此响应代入式(2)中，得到对应的特征方程：

(4)

使式(4)成立，则式(5)为：

(5)

方程值ω1,ω2,…,ωn为系统的每一阶自然圆频率，且有ω1<ω2<…<ωn，对应的频率为fi=ωi/2π。系统一般存在n个共振频率和振型，ω1为系统的第1 阶共振频率，它常常对系统的动态特性有关键影响。

3.2 模态分析求解

考虑到落纱装置工作过程中，其中步进电动机工作时最高转速n为1 000 r/min，所引起的激振频率[10]f=n/60≈16.67 Hz，取安全系数为1.5。因此为了避免共振，落纱架的固有频率应尽量避开电机的激振频率：16.67×1.5=25.005 Hz。

运用ABAQUS对落纱架进行模态分析，求解方法采用Lanczos法,依据电动机的激振频率，选取前4阶振型如图8所示。

图8 前4阶振型图Fig.8 The first 4 modes.(a)First mode;(b)Second mode;(c)Third mode;(d)Fourth mode

根据模态分析的振型图和模态分析结果表2可得：其中第1阶固有频率偏低，接近电动机的激振频率，因此有必要改进结构提高固有频率，使其尽量远离电动机的激振频率；产生最大变形的地方位于托板的边缘处，后续将进行拓扑优化改进托板结构。

表2 模态分析结果Tab.2 Modal analysis results.

4 托板优化设计

4.1 拓扑优化理论

拓扑优化是在给定的负载工况、约束条件下，在给定的部位优化材料分布的方法。

根据托板结构，采用连续体结构拓扑优化的变密度法(SIMP法)，其在假定的密度和材料弹性模量之间引入惩罚因子，假定设计材料密度与其弹性模量的非线性关系，引入的惩罚因子在(0,1)之间，使密度值从中间向(0,1)接近，从而把找寻结构最优的拓扑问题转化为找寻最优材料分布的问题；引入SIMP法后的结构的材料弹性模量、刚度矩阵、柔度和敏度如下所示[11]：

(6)

ΔE=E0-Emin

(7)

Emin=E0/1 000

(8)

式中：Ep为插值后的弹性模量；Emin为空洞弹性模量；E0为固体弹性模量；xi为单元i的设计变量；p为惩罚因子；K为整体刚度矩阵；Ki为单元刚度矩阵；C(x)为结构柔度值；U为位移向量;C′(x)为结构灵敏度。

4.2 托板拓扑优化

为提高落纱架的固有频率及实现托板的轻量化设计，采用应变能最小化(即柔度最小化)来最大化落纱架刚度作为拓扑优化的目标函数，约束条件为设计区域的重量约束，基于SIMP法建立托板拓扑优化数学模型：

(9)

式中：xi为单元密度设计变量；n为离散后的单元数；M(x)为优化后的托板质量，kg；M*为托板原始质量约束；F为载荷向量。

将托板有限元模型进行静态分析之后，进入优化模块进行分析，如图9所示，经过20次迭代后，目标函数趋于收敛，得到托板材料的最佳分布密度云图，如图10所示，灰色区域的单元密度趋于1，此区域结构材料保留，黑色区域的单元密度趋于0，此区域结构材料可以部分去除。

图9 目标函数随迭代次数的变化曲线Fig.9 Change curve of the objective function with the number of iterations

图10 托板材料分布密度云图Fig.10 Distribution density cloud map of pallet material

结合托板的实际情况，在满足托板强度的前提下，依据拓扑优化的材料分布情况和实际工艺性[12]，对原托板结构进行如下改进：①合理去除部分材料；②在薄弱部位处增加三角肋板。改进后的托板实体模型如图11所示。

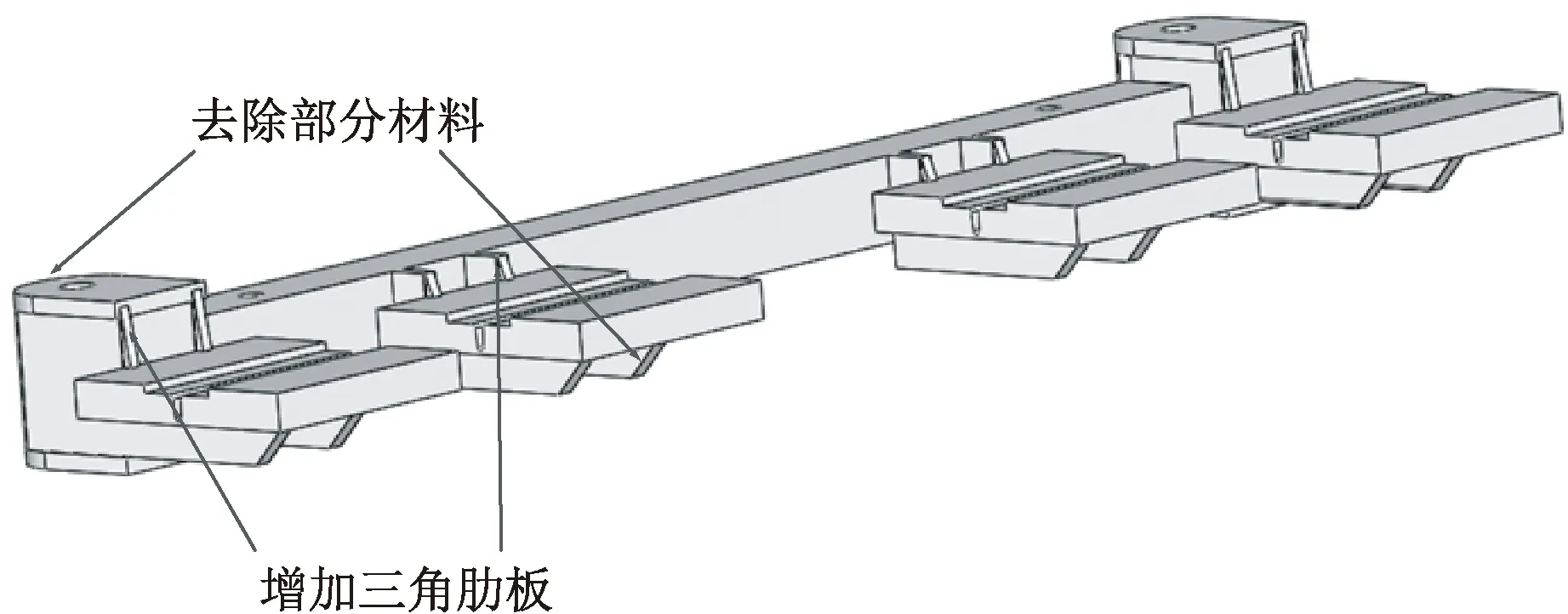
图11 改进后的托板实体模型Fig.11 Improved pallet solid model

5 优化前后的落纱架的动态特性分析

5.1 模态分析

将改进后的托板装配到落纱架中，在相同边界条件下再次进行模态分析，原结构与优化后的结果对比如表3所示，可以看出优化前后落纱架的振型基本不变，优化后的托板质量减少了5.2%，同时落纱架的各阶固有频率都有所提高，尤其是前2阶固有频率提高了25.4%和37.4%，因此达到了提高落纱架固有频率及实现托板轻量化设计的目的。

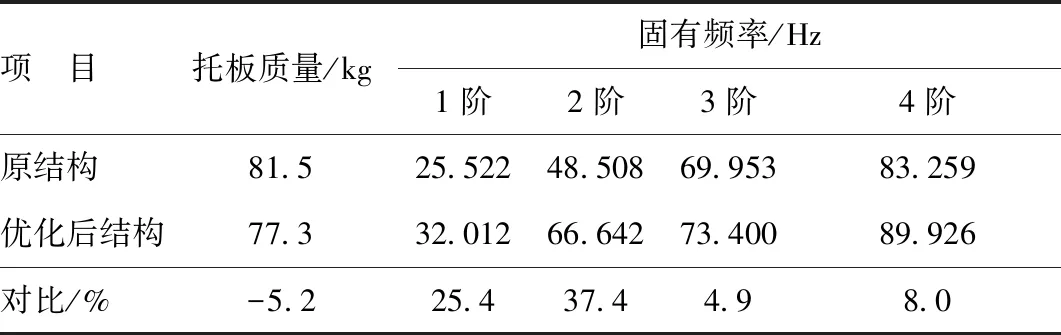
表3 结构优化前后结果对比Tab.3 Comparison of results before and after structural optimization

5.2 谐响应分析

谐响应分析[13]常用于确定系统在承受随时间按正弦(简谐)规律变化的载荷时的稳态响应，分析的目的是得出振幅-频率响应曲线，使研究工作者能够预测共振及其他由受迫振动引发的不利影响。由经典力学可知谐响应分析的微分方程：

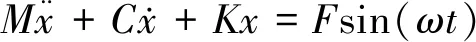
(10)

通过模态分析，可以发现变形最大的部位在托板边缘处，因此对这个位置进行谐响应分析，考虑到丝杠带动托板升降有提升力，因此设置托板Y方向2个等大的提升力作为谐振力进行分析，分别得到结构优化前后X、Y、Z3个方向的位移-频率响应曲线[14]以及总位移-频率曲线，如图12～15所示。

图12 X方向的位移-频率响应曲线Fig.12 X-direction displacement-frequency response curve

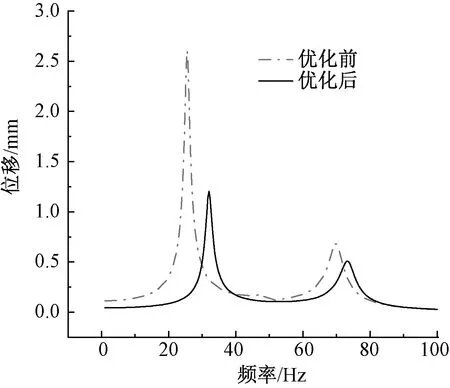
图13 Y方向的位移-频率响应曲线Fig.13 Y-direction displacement-frequency response curve

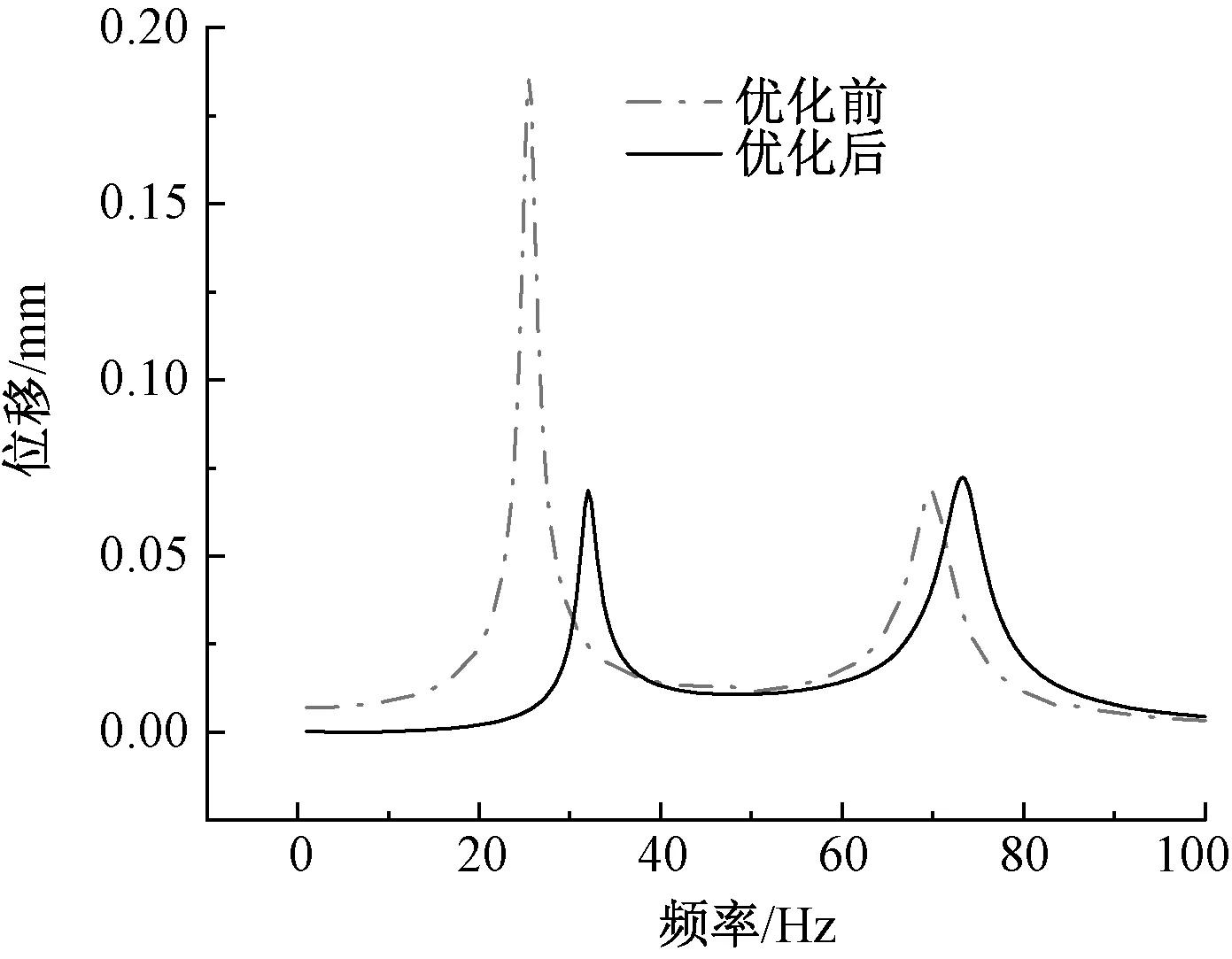
图14 Z方向的位移-频率响应曲线Fig.14 Z-direction displacement-frequency response curve

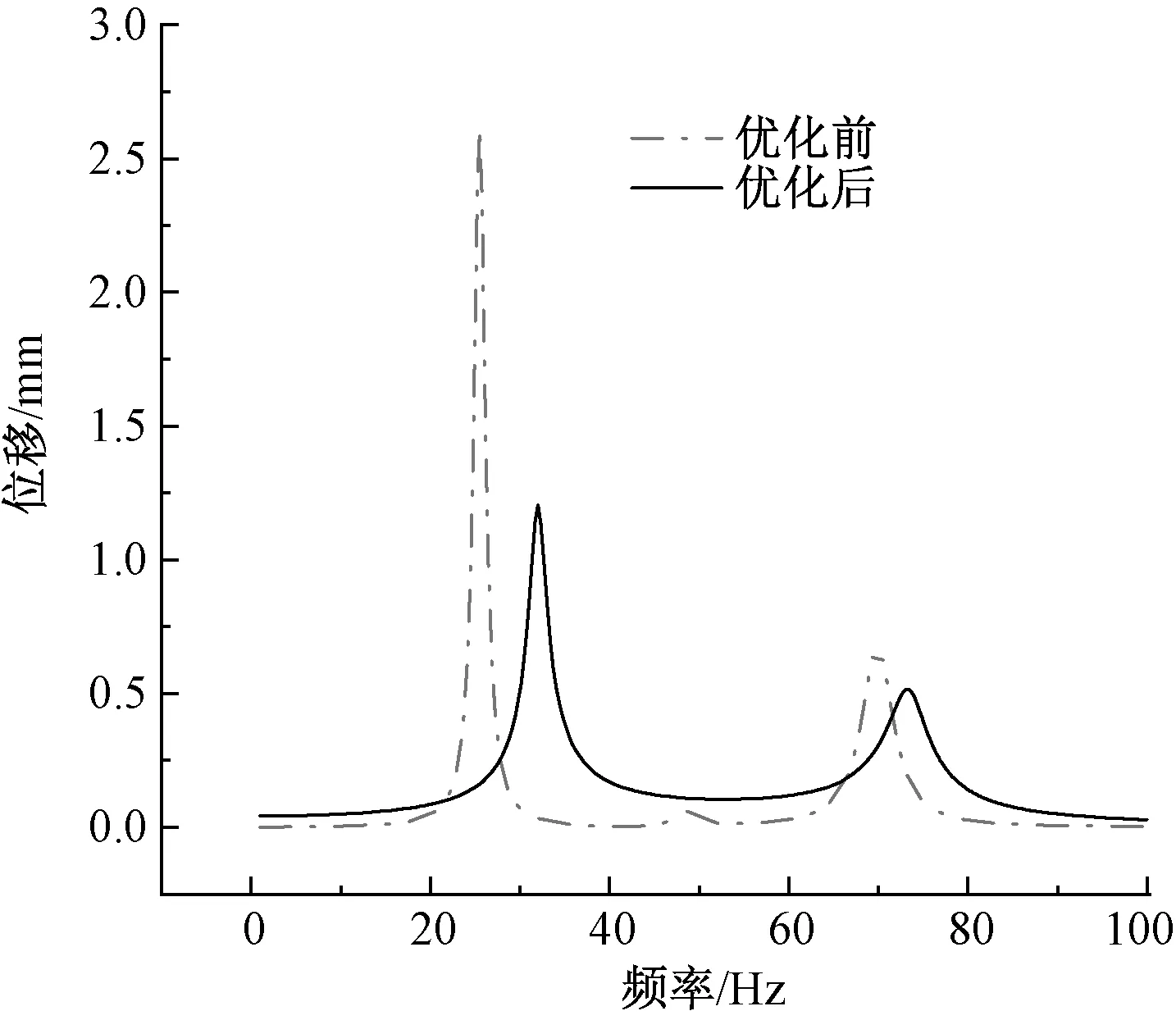
图15 总位移-频率响应曲线Fig.15 Total displacement-frequency response curve

依据托板优化前后落纱架的位移—频率响应曲线图和表4可得：落纱架在30 Hz和70 Hz左右(接近模态分析中的第1阶和第3阶固有频率)时的振幅较大，并且优化后的X、Y、Z3个方向的位移响应峰值对应的频率均有所提高，位移响应峰值均有所减少，X、Y、Z3个方向位移峰值分别减少了16.2%、52.5%、63.2%，总位移峰值减少了54.8%，因此落纱架的动态特性得到明显改善。

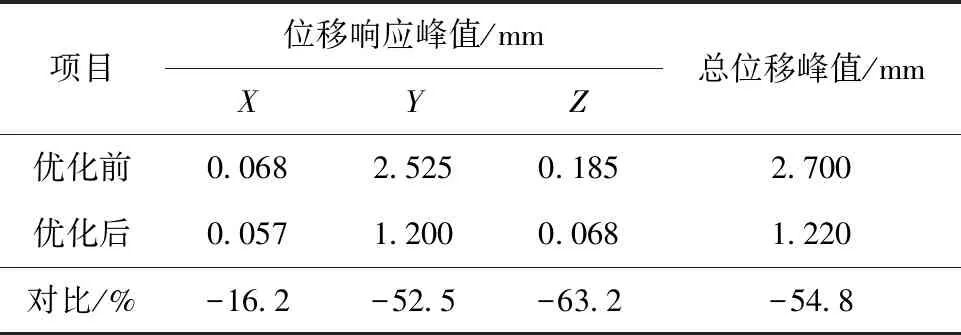
表4 结构优化前后位移峰值对比Tab.4 Comparison of peak displacements before and after structural optimization

6 结 论

针对传统粗纱机人工落纱效率低和劳动强度大等问题，对粗纱机进行技术改造，设计了一种集体自动落纱装置，包括水平移动机构、竖直移动机构以及粗细联输送机构。此装置可与不同型号的粗纱机配套使用，不仅降低工作强度，还大大提高落纱效率，同时避免纱管损坏，具有广阔的市场应用前景。

因装置的稳定性好坏直接影响落纱工作正常进行，故分析了关键部位落纱架优化前后的动态特性。结果表明：优化后托板的质量减少了5.2%，落纱架前2阶共振频率提高了25.4%和37.4%，托板边缘处X、Y、Z3个方向振幅峰值分别减少了16.2%、52.5%、63.2%，提高了装置的稳定性，验证了连续体结构拓扑优化的变密度法对于结构优化设计的有效性，为后续整体装置的样机试制提供理论基础。