Robust TDOA/FDOA estimation from emitter signals for hybrid localization using UAVs

Yu-bing Wang ,Xiao-long Liang ,Jia-qiang Zhang ,Bao-xiang Ren ,Ke Jin

a Air Traffic Control and Navigation College,Air Force Engineering University,Xi’an,China

b Shaanxi Key Laboratory of Meta-synthesis for Electronic &Information System,Xi’an,China

c National Digital Switching System Engineering and Technological Research Center,Zhengzhou,China

Keywords:TDOA FDOA Parameter estimation Doppler ambiguity Hybrid localization

ABSTRACT This paper considers the time difference of arrival (TDOA) and frequency difference of arrival (FDOA)estimation problem for joint localization using unmanned aerial vehicles (UAVs),involving range migration (RM) and Doppler ambiguity within observation interval.A robust estimation method based on interpolation and resampling is proposed.Specifically,the interpolation artificially increases the pulse repetition frequency (PRF).After that,the resampling eliminates the coupling between range frequency and slow time.Finally,a coherent integration step based on inverse discrete Fourier transform (IDFT) is used to achieve parameter estimation and suppress the grating lobes caused by interpolation.The proposed method could be efficiently implemented by fast Fourier transform(FFT),inverse FFT(IFFT)and non-uniform FFT(NUFFT)without parameter searching procedures.Numerical experiments indicate that the proposed method has nearly optimal anti-noise performance but much lower computational complexity than the maximum likelihood estimator,which makes it more competitive in practical applications.

1.Introduction

Cooperative localization using UAVs has been widely used in military applications,such as radar reconnaissance [1].There are several kinds of measurements can be used in passive localization,including time-difference-of-arrival (TDOA) [2],angle-of-arrival(AOA) [3],received signal strength (RSS) [4],etc.When the radar and the UAV sensors are relatively moving,it is efficient to apply frequency-difference-of-arrival (FDOA) to enhance the estimation performance.The combination of different measurements can improve the localization accuracy,and therefore the TDOA/FDOA hybrid localization has drawn great attention in both theoretical analysis and practical trail[5].

The essential parameters in TDOA/FDOA localization are time differences and frequency differences,respectively.These parameters can be estimated by processing the emitter signals received by spatial distributed sensors.Especially in non-cooperative scenarios,even though there are no prior knowledge of the signals and noises,the localization of radar can be realized by calculating TDOA/FDOA[6].Thus,the estimation performance and anti-noise performance of TDOA/FDOA have significant influence on localization accuracy.

For TDOA/FDOA estimation,two challenges gradually appear with the development of radar and localization technology.The first one is that the signal processing object changes from single pulse to pulse train.The second one is that existing estimation algorithms fails to achieve a good compromise between computational complexity and anti-noise performance.

For TDOA/FDOA estimation using a single pulse,the most representative methods are the cross ambiguity function (CAF)[7]and its variants [8-10].These methods achieve estimation by performing parameter searching,which inevitably leads to high computational complexity and is not unacceptable in practical applications.In this case,several Fourier transform-based and iteration-based methods are proposed in Refs.[11-13]to speed up the implementation of parameter searching procedures.However,when the received radar signal becomes pulse train,TDOA/FDOA will change with movement of sensors.During the long-term reconnaissance,range migration (RM) will appear which spreads the signal energy across multiple time and Doppler cells.Consequently,conventional single-pulse-based methods will suffer serious performance loss and even no longer works [14].

Obviously,using pulse train helps to improve the estimation accuracy.In recent years,estimation algorithms based on longterm coherent integration technique have been developed rapidly[15-19].The well-known maximum likelihood estimator (MLE)enjoys the optimal performance in estimation accuracy and antinoise character under Gaussian noise environment [20-22].This method integrates the signal energy by parameter searching and phase compensation.Therefore,the computational complexity is also daunting.Inspired by the processing method in synthetic aperture radar,an estimation method based on Keystone transform(KT) is proposed in Ref.[14].Without knowing the motion parameters,KT could eliminate the RM by rescaling the slow time for each range frequency [23].Nevertheless,when Doppler ambiguity happens,fold factor searching will inevitably increase its complexity.In Ref.[6],Liu et al.proposed an efficient estimation method based on frequency symmetric autocorrelation function(FSAF)and scaled Fourier transformation(SFT),namely FSAF-SFT.In this method,the RM is corrected by SFT and the implantation could be achieved via fast Fourier transform(FFT)and inverse FFT(IFFT).Unfortunately,the FSAF operation will introduce interference between signal and noise,which sacrifices about 6 dB anti-noise performance to obtain efficiency [16,24].After that,the frequency reversing transform (FRT) and SFT,i.e.,FRT-SFT,is proposed in Ref.[25].Different from FSAF,the FRT defined a frequency correlation function with constant delay.Consequently,it has inferior performance under low signal-to-noise (SNR) environment.

In this paper,we focus on TDOA/FDOA estimation using pulse train for radar localization.A novel method based on interpolation and resampling is proposed.The method achieves coherent integration of multiple pulses,which compensates for the time-varying of TDOA and Doppler ambiguity of FDOA during the observation interval.The advantage is that it has nearly optimal estimation performance in white Gaussian noise environment,but it can be efficiently implemented via non-uniform FFT (NUFFT) [26].

The remainder of this paper is organized as follows.The signal model is established in Section 2.Section 3 derives the principle of the proposed method in detail.Efficient implementation and computational complexity are analyzed in Section 4.Numerical experiments are carried out in Section 5.Finally,Section 6 concludes our work.

2.Signal model

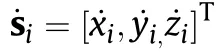
Before deriving the proposed method,some hypotheses and constraints are listed below.

(a) There is no synchronization error between the two UAVs.

(b) Each UAV can obtain its own location accurately.

(c) The proposed method is not suitable for frequency agile radar.

(d) Only the white Gaussian noise is considered and no other interference is received by the receivers.

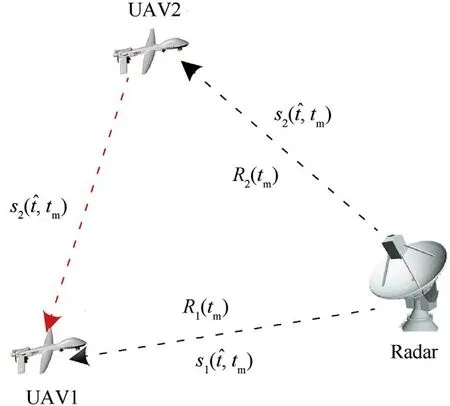
Fig.1. Localization scenario of two UAVs against one target.

Without loss of generality,we assume that a coherent radar transmits linear frequency modulated (LFM) pulse trains,which could be expressed as

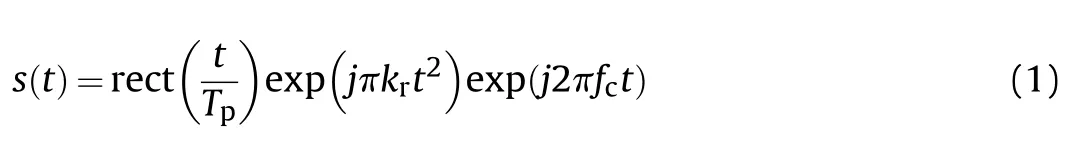
where t is the time,Tis the pulse duration,kis the chirp rate of LFM signal,and fdenotes the carrier frequency.

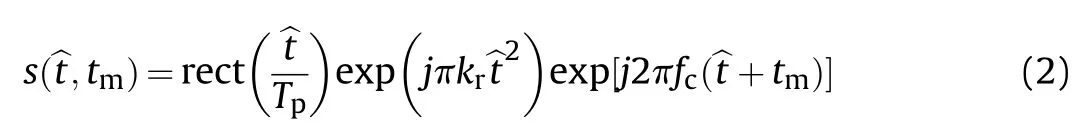
The batch architecture of the transmitted signal is shown in Fig.2.

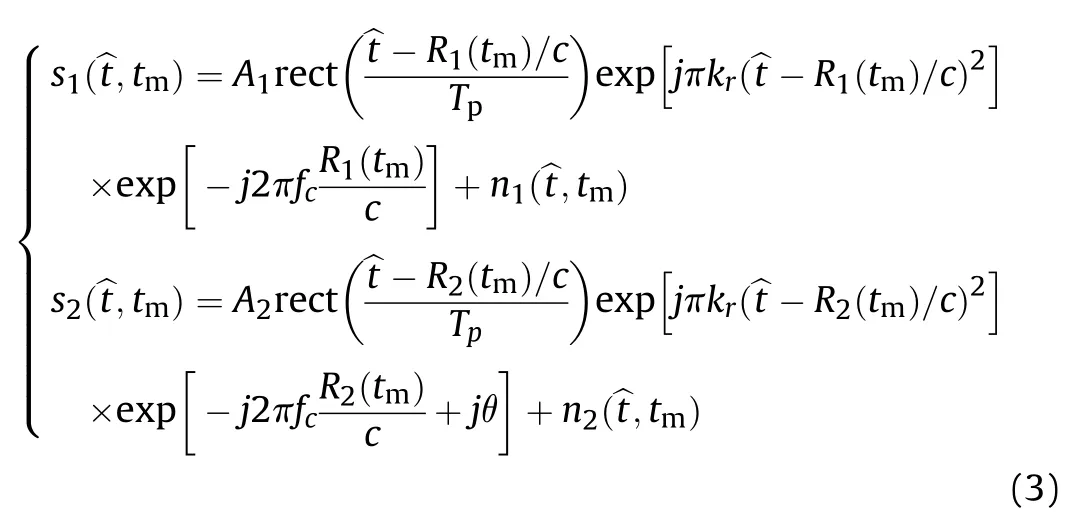
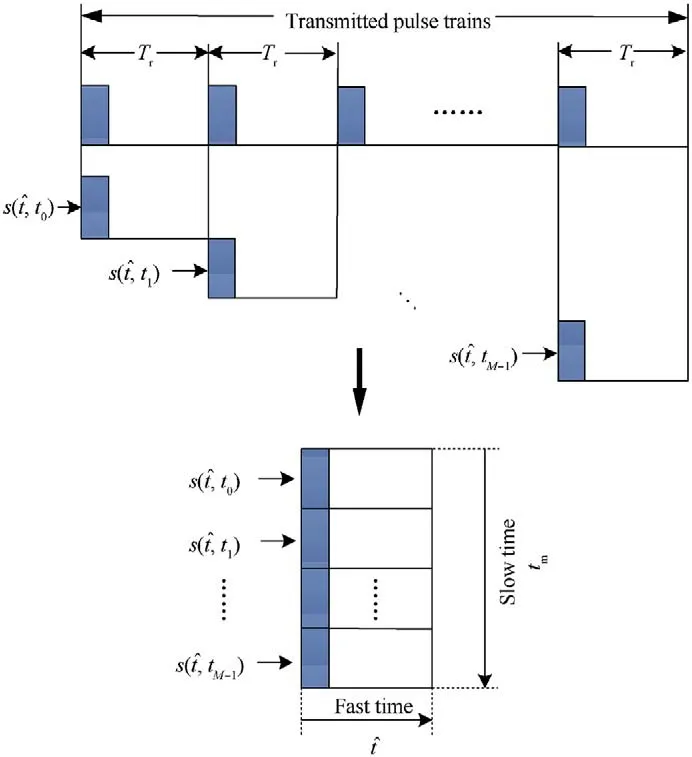
Fig.2. Batches architecture of the radar signal.

In the applications of joint localization with two UAVs,the radar parameters could be obtained via electronic reconnaissance.When receiving synchronously,the received based band signals of UAV1 and UAV2 are delay versions of the transmitted signals,i.e.,

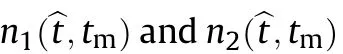
Let UAV1 be the reference station,the received pulse trains could also be processed by the batch architecture,as shown in Fig.3.

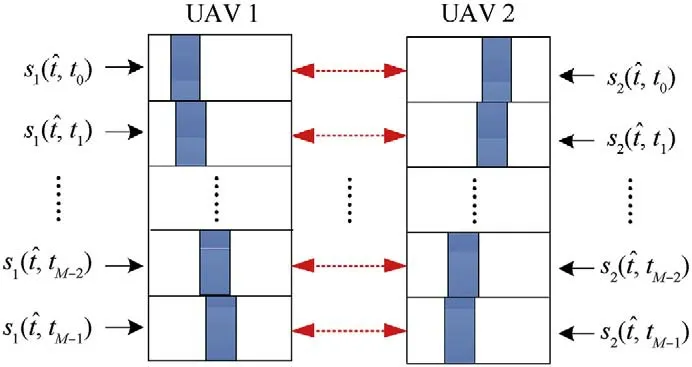
Fig.3. Batches architecture of the received signal.

3.Proposed TDOA and FDOA estimation method

3.1.Demodulation

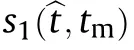
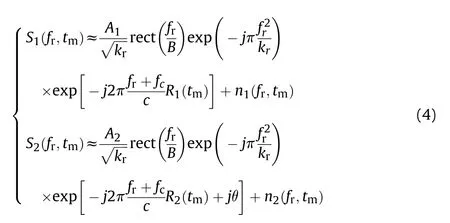
where fis the range frequency variable and B=kTis the bandwidth of the radar signal.

Multiplying S（f，t）by the conjugate of S（f，t）yields

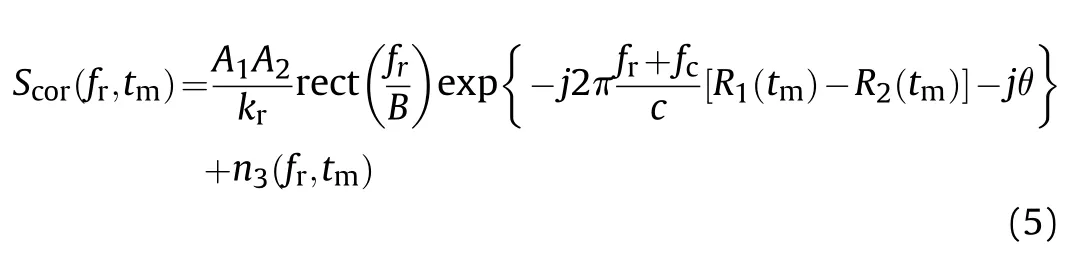
where n（f，t）denotes the interference terms.

In (5),the linear frequency modulation is successfully eliminated.It is clear that the cross-correlation operation in (4)and (5)eliminates signal modulation through conjugate multiplication,which does not depend on radar parameters.Therefore,the demodulation method can also be applied to other common radar signals,such as nonlinear LFM signal,phase-coded signal,and so on.However,this process cannot be used to frequency agile radar,as the time-varying carrier frequency produces random phase,which will affect coherent integration[25].

Performing inverse FT (IFT) with respect to f,we get

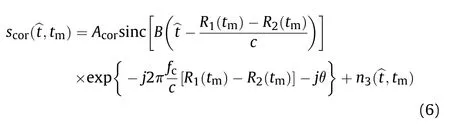
From (6) it is easy to find that,the sinc function reflects the position of envelope and the exponential term represents the Doppler frequency.Obviously,ΔR（t）=R（t）-R（t）is of interest to us because it contains information about the TDOA and FDOA.The geometry relationships of localization are as follows:

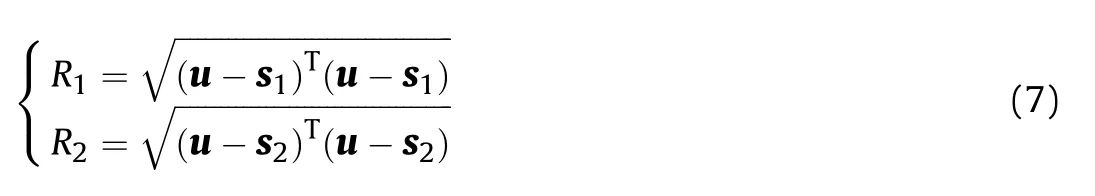
Within the observation time,the UAVs move to new positions whose coordinates are

Thus,the new distance between the target and UAVs are as follows:

During the reconnaissance and positioning interval,the highorder terms could be neglected.Thus we have

denotes the initial range difference (IRD) and radial velocity difference(RVD) respectively.

The TDOA and FDOA could be derived from IRD and RVD,i.e.,

Insert (10) into(6) and (5) yields

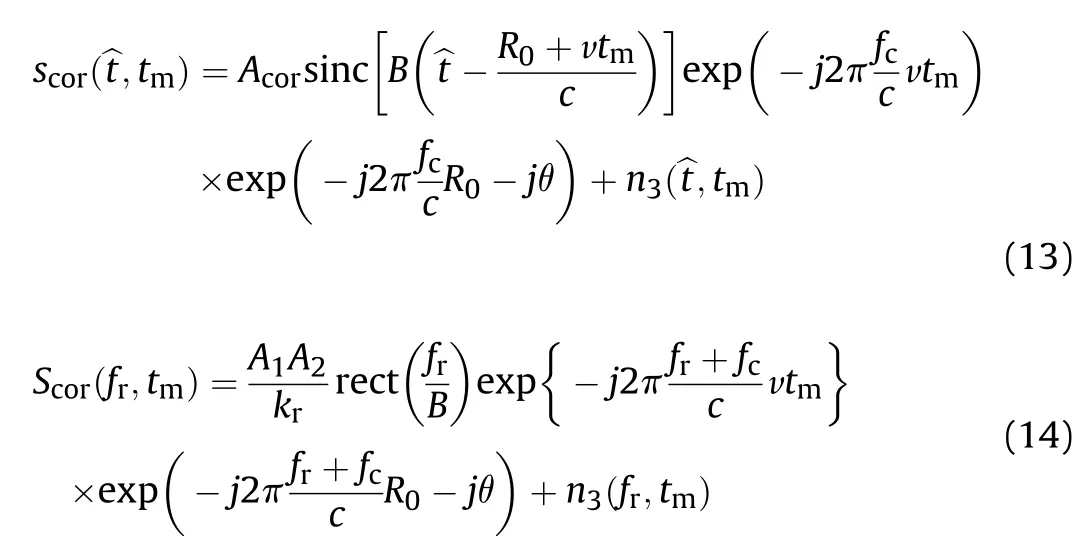
In the following part,we will focus on the estimation of TDOA and FDOA.

3.2.FDOA ambiguity and interpolation

3.2.1.Doppler ambiguity

As shown in(13),the signal envelope changes linearly with the slow time.When the offset exceeds the range sampling resolution Δr=c/f,the RM could not be ignored,where fis the sampling rate.The RM effect disperses the signal energy over several range bins and will lead to incorrect estimation of IRD and thus TDOA.From(14),we could also find that the coupling between fand tis the essential cause of envelope migration.

Moreover,as the RVD increases,frequency ambiguity will also appear,i.e.,｜fv/c｜＞f/2.In this case,the RVD should be expressed as [28].

where vis the blind speed,nis the fold factor,vis the ambiguous velocity,and mod（·）denotes the remainder function.

The derivation is performed in the range frequency-slow time domain.Insert(15) into (14) gives

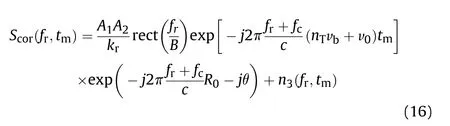
The discrete form of (16) in slow time can be written as

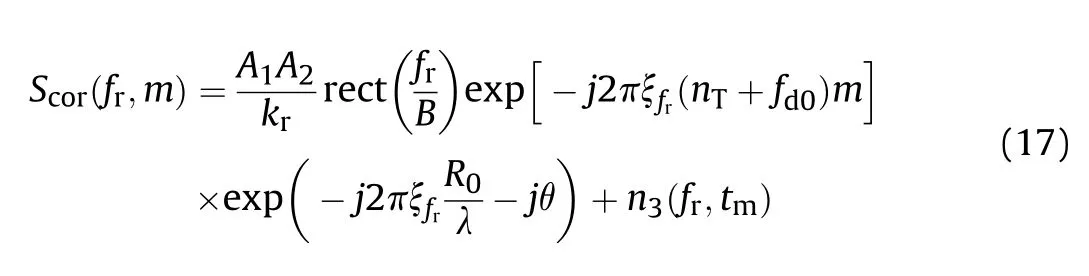
As the FDOA is constant along the slow time,conventional methods usually perform discrete Fourier transform (DFT) along the slow time to estimate the parameter,i.e.,

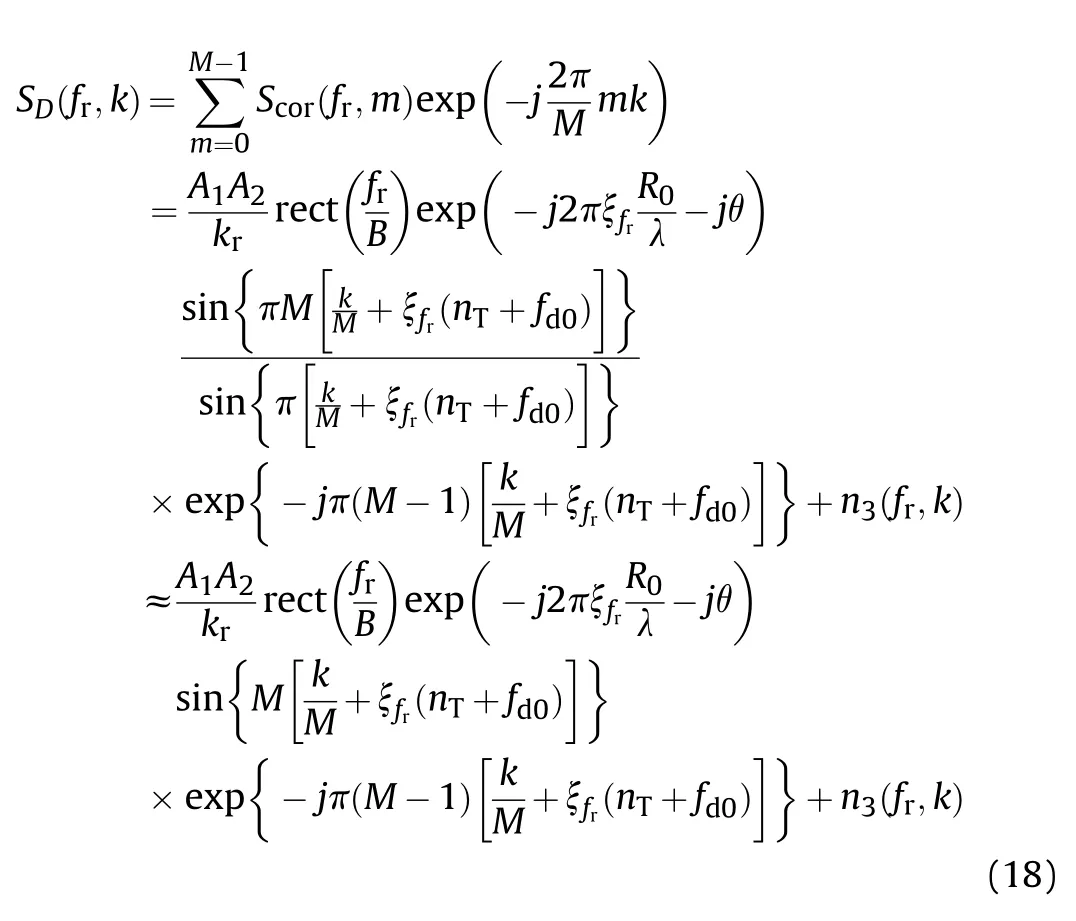
where k=0，1，…，M-1 represents the discrete Doppler frequency.

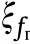
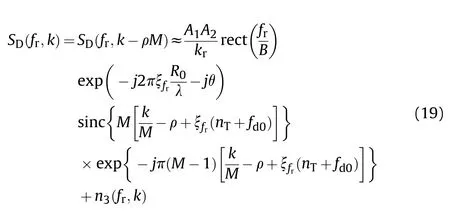
where ρ is an integer indicating the ambiguity number.

Consequently,the Doppler peak should be located at

Fig.4 simulates the estimation result using DFT method.The parameters are f=3 GHz,B=30MHz,T=10μs,f=36MHz,M=500,f=500Hz,R=3km,v=90m/s.The TDOA is R/c=10μs and the FDOA is -fv/c=-900Hz.The digital FDOA is -（n+f）=-1.8.The result of demodulation and DFT are shown in Fig.4(a) and (b),respectively.

As shown in Fig.4(a),the signal envelope migrates linearly with the slow time and the offset is 90 m.Therefore,the TDOA could not be accurately estimated.The DFT result is given in Fig.4(b)and the digital FDOA values are around 2-（n+f）=0.2,which is caused by ambiguity.Therefore,conventional DFT-based method no longer works in estimating TDOA and FDOA.

As analyzed above,the migrating TDOA and the folded FDOA are caused by the coupling term and ambiguity,respectively.Firstly,we focus on the ambiguity problem.

3.2.2.Interpolation

The essential reason for frequency ambiguity is the insufficient sampling rate of slow time.Thus,a simple method to solve ambiguity is to increase the sampling rate,which,however,is dependent on the radar’s PRF and cannot be changed casually.In this paper,we introduce the interpolation method into slow time.

Assume the interpolation rate is I,the interpolated signal could be written as

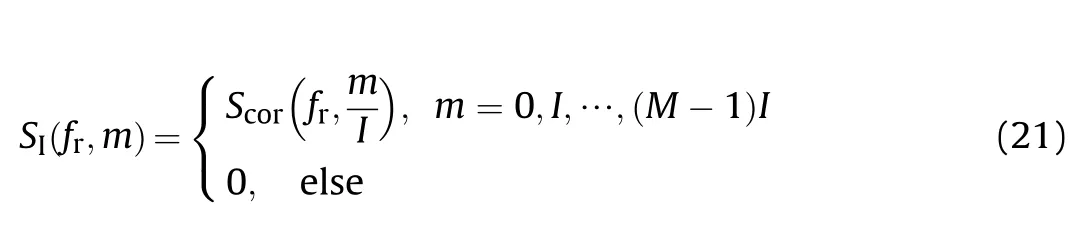
Eq.(21)means that we artificially add（I-1）zeros between two sampling data of S（f，m）.In this way,the sampling rate has been increased to I·f.The MI-point DFT of S（f，m）can be expressed as

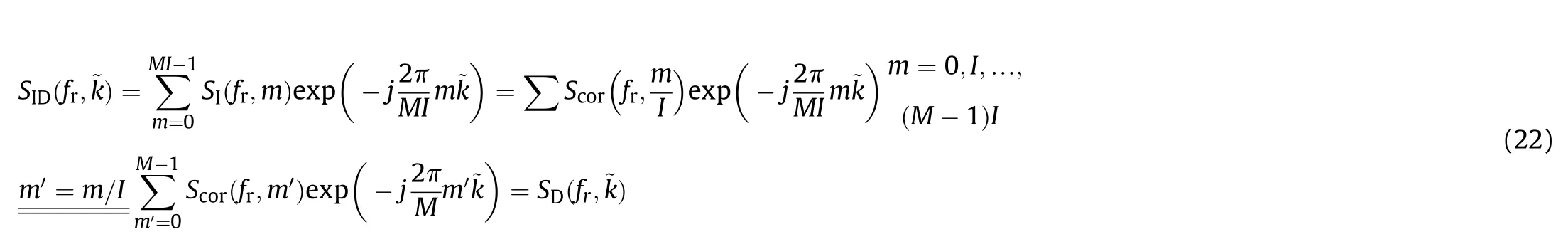
Thus,we have

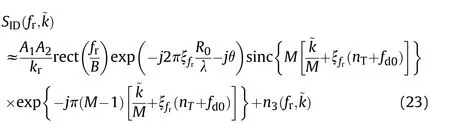
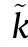
The difference between (24) and (20) lies in the scope of measurable FDOA.As the sampling rate is increased to I·f,the scope is accordingly extended by I times.Since the FDOA is usually non-cooperative,the interpolation rate could be determined according to the interested scope.

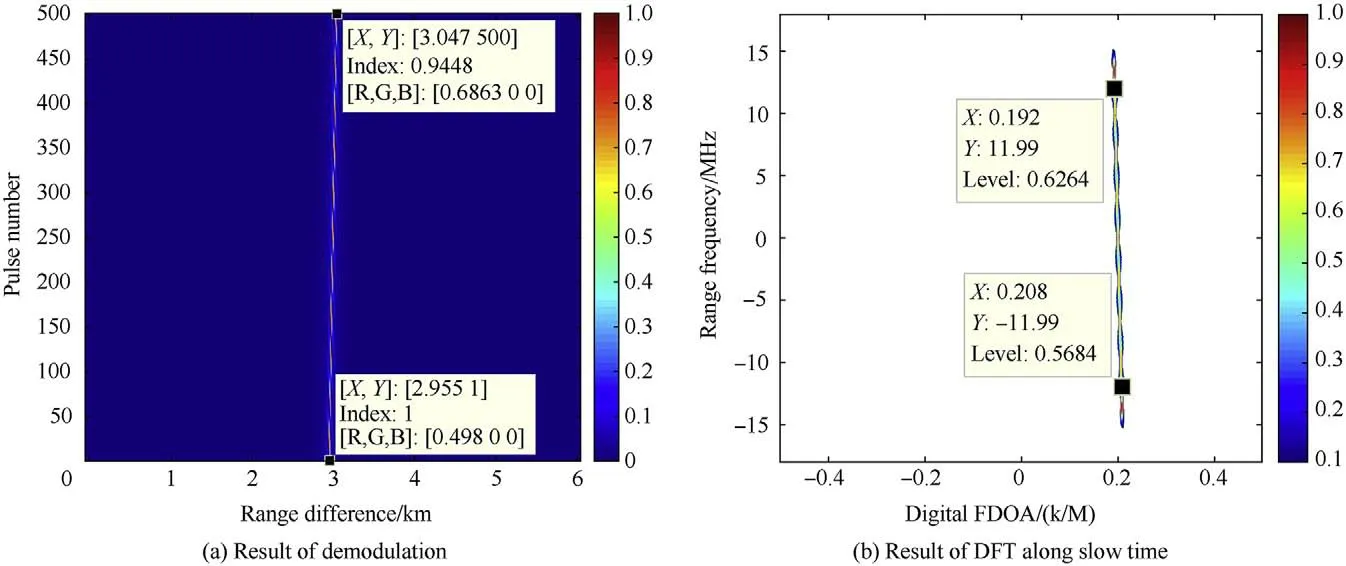
Fig.4. Migrations of TDOA and FDOA.

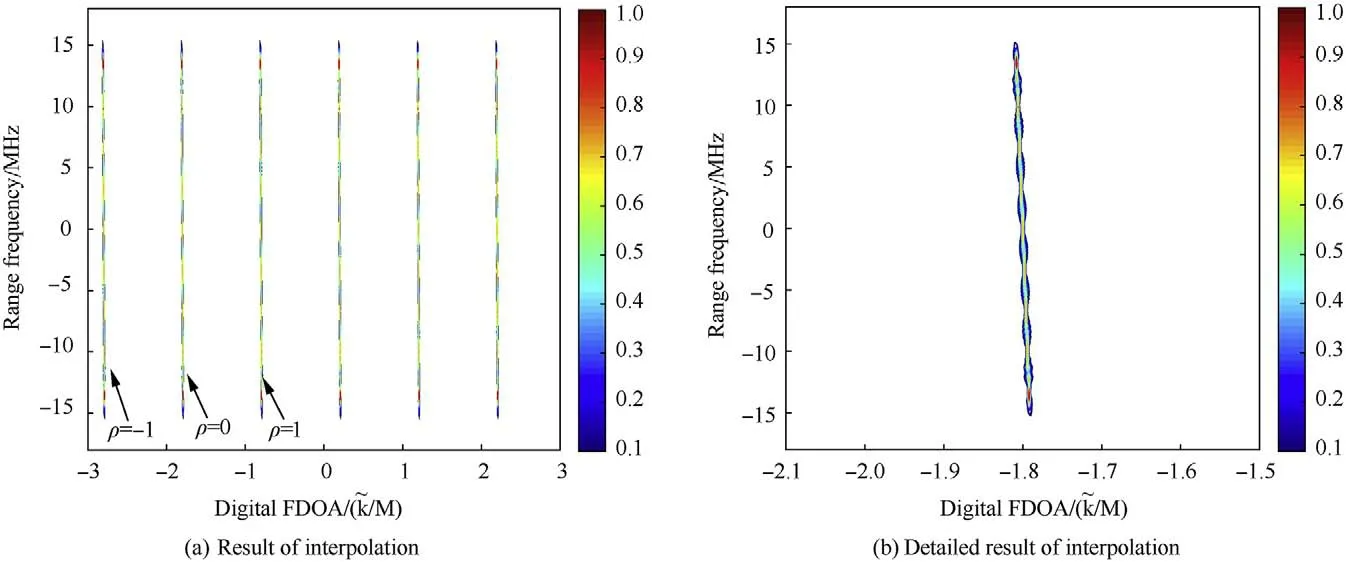
Fig.5. Working principle of interpolation.

One may find that,the interpolation will not bring more information about the signal and the result is only a periodic duplicate of(20).However,this step allows us to observe the unambiguous Doppler peak at least.

This example gives the estimation result using interpolation method.The parameters are the same with those in Example 1.The interpolation rate is I=6.The result is shown in Fig.5.

In Fig.5(a),we could see I spectrum lines caused by interpolation,and the scope of digital FDOA is also extended by I times.The true unambiguous spectrum line is marked by ρ=0.Its detailed result is given in Fig.5(b).

From Example 2,we may conclude two problems unsolved.

(a) The interpolation process just duplicates the spectrum lines and the true one is not recognized.

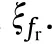
In subsection 3.3,we focus on eliminating the coupling term.The recognition method is given in the following subsection 3.4.

3.3.Resampling

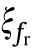
where Γ（·）is the resampling operation and performs the variable substitution,which is defined as

Consequently,Eq.(25) can be written as

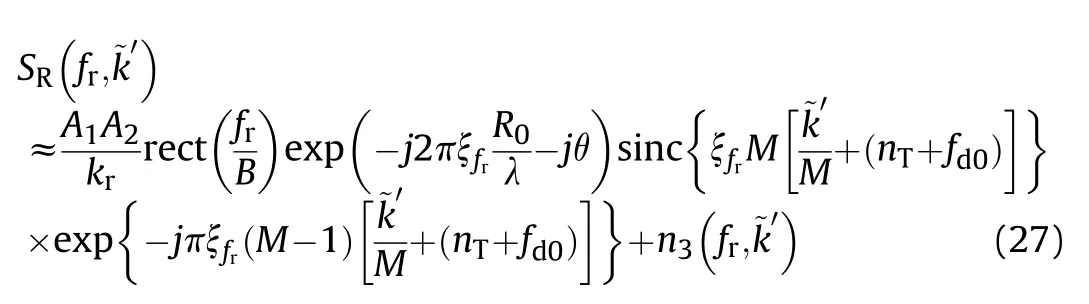
The Doppler peaks are now located at

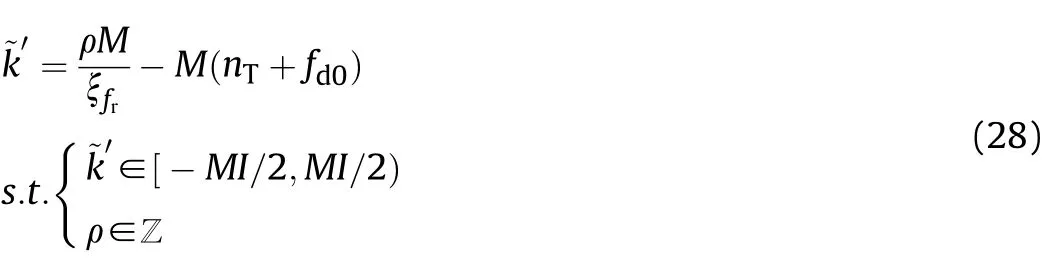
Fig.6 gives the results of resampling.The parameters are the same with those in Example 2.

It can be seen from Fig.6(a) and (b),after resampling only the spectrum line of ρ=0 is corrected into straight.The digital FDOA is-1.8,which is consistent with the theoretical value.As shown in Fig.6(c)and(d),the lines corresponding to ρ≠0are oblique,which means the coupling still exists.

3.4.Parameter estimation

As analyzed in subsection 3.2,the interpolation process duplicates the result of DFT.Therefore,we could see I-1 false spectrum lines.However,the resampling result provides us a simple method to recognize the true spectrum line.As shown in(28)and Fig.6(a),only the true spectrum line is straight while the false ones are not.Thus,we just need a method to detect the straight line.

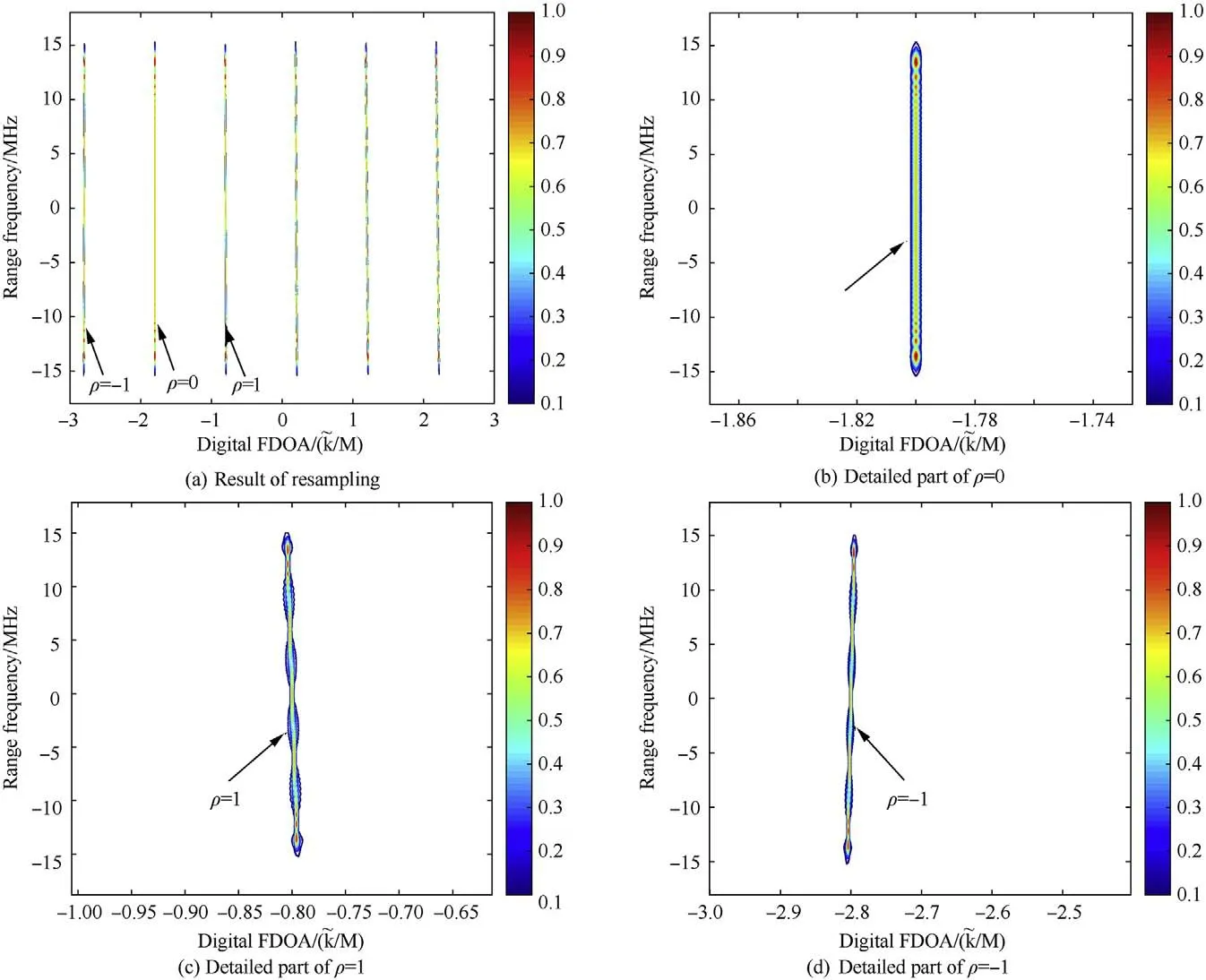
Fig.6. Working principle of resampling.

For the envelope,only the true spectrum line is aligned.For the phase in a certain Doppler frequency cell,its value is

where

Finally,the TDOA and FDOA could be estimated as

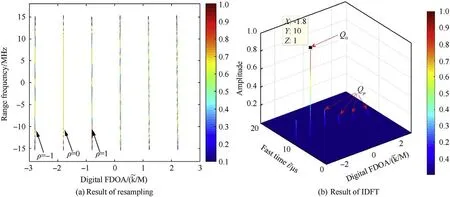
Fig.7. Recognition and parameter estimation.

Fig.7 gives the IDFT results of Example 3.The parameters are the same with those in Example 2.

It is obvious in Fig.7 that,only the true spectrum line is concentrated as a sharp peak while the false ones cannot be well integrated.In this way,the recognition process is achieved and the parameters are estimated.

3.5.Summary of algorithm flow

As shown in Fig.8,the detailed implementation of the proposed algorithm is summarized as follows.

Step 1:Perform batching and fast time FFT for the signals of UAV1 and UAV2 to obtain S（f，t）and S（f，t）.

Step 2:Multiply S（f，t）by the conjugate of S（f，t）to obtain S（f，t）.

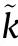
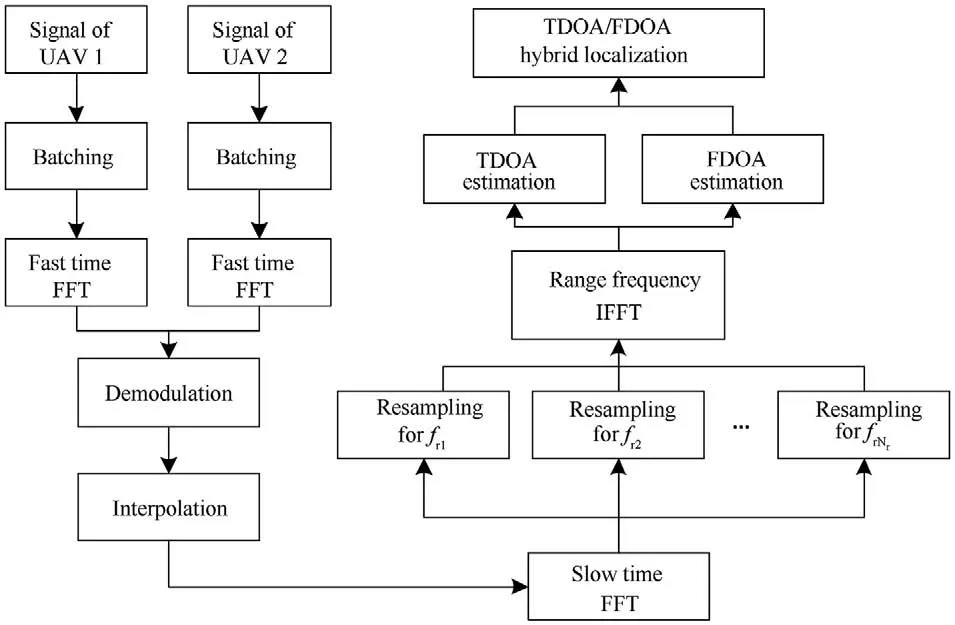
Fig.8. Flowchart of the proposed method.

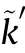
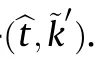
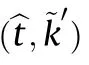
4.Efficient implementation and complexity analysis

4.1.Efficient implementation

In our proposed algorithm,the resampling step is usually achieved by interpolation[30,31],which,of course,is time consuming and will introduce much numerical errors.Combining the slow time FFT and resampling,we present an efficient and more accurate implementation based on NUFFT.

The slow time FFT and resampling can be combined as

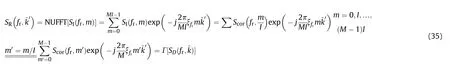
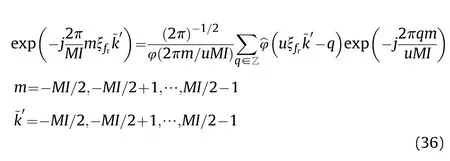
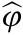
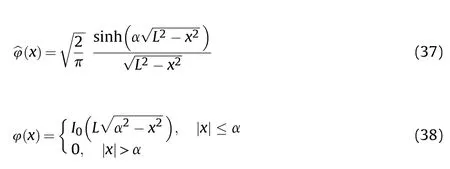
where I（·）is the modified Bessel function of the first kind with zero order,L is length of Kaiser-Bessel window,and α is factor slightly smaller than π（2 -1/u）.In this paper,we choose α=π（2-1/u）-0.01 and L=6.

Inserting (36) into(35) yields

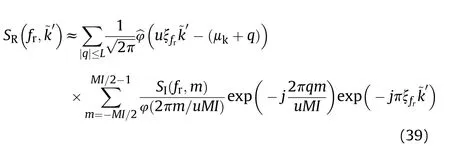
By(39),the NUFFT could be efficiently achieved via standard FFT and have much higher accuracy than interpolation.3.

4.2.Computational complexity

In this section,the computational complexity of the proposed method is analyzed in detail.The representative MLE,FSAF-SFT,FRT-SFT,and CAF methods are selected for comparisons.Denote the number of pulses,fast time samples,searching TDOA,and searching FDOA by M,N,Nand N,respectively.The DFT,IDFT,and NUFFT are efficiently implemented by FFT and IFFT.

For MLE,it achieves parameter estimation by performing 2D brute-force searching,phase compensation and IFFT.Hence,its computational complexity is in the order of O（NMNlogN）.

For FSAF-SFT,its main procedures include the FSAF(O（3NMlogN）),the Chirp-Z based SFT along the slow time(O（3NMlogM）),and IFFT of the range frequency(O（NMlogN）).Thus,the overall computational complexity isabout O（3NMlogM +4NMlogN）.

For FRT-SFT,it completes parameter estimation via fast time FFT(O（NMlogN）),FRT operation(O（MN）),Chirp-Z transform[32,33]based SFT along the slow time (O（3NMlogM）),and range frequency IFFT (O（NMlogN）).Therefore,the total burden is about O（2NMlogN+3NMlogM）.

As for CAF,it could be achieved via FFT.For each searching TDOA,a IMN-point FFT is required with the computational cost O（IMNlogIMN）.Thus,the total computational complexity is in the order of O（IMNNlogIMN）.

The main procedures of the proposed method include fast time FFT(O（2NMlogN）),interpolation (ignored),NUFFT-based resampling (O（uNIMloguIM）) and range frequency IFFT.So,the overall computational complexity is in the order of O（uIMNloguIM）.

The computational complexities of the above methods are listed in Table 1.Under the assumption of M=N=Nτ,Nν=IM,I=6,and u=2,Fig.9 visually shows the computational cost.The time cost when M=500 is also given.Compared with MLE and CAF,the proposed avoids parameter searching and can be efficiently implemented via NUFFT.Thus,a much lower burden is suffered.Compared with FASF-SFT and FRT-SFT,the proposed method has much superior anti-noise performance,which will be evaluated in subsection 5.2.

Table 1 Computational complexity evaluation.

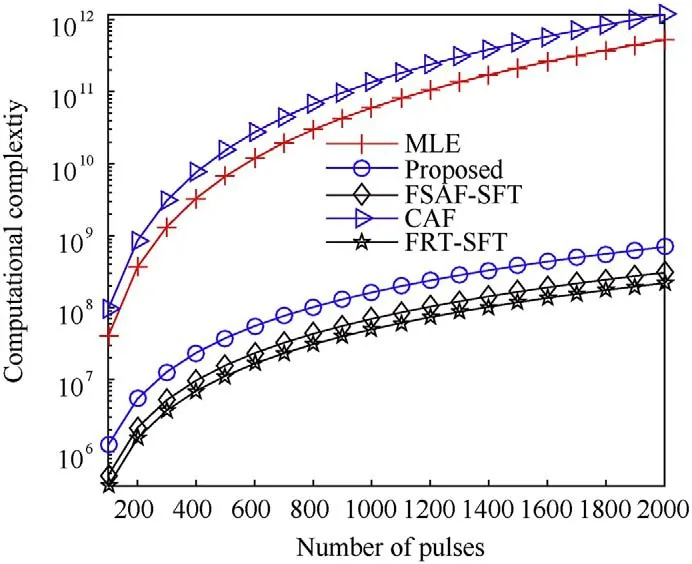
Fig.9. Computational complexity of different methods.

5.Numerical experiments

In this section,several numerical experiments are conducted to investigate the effectiveness of the proposed method.

5.1.Estimation performance

In this part,the parameter estimation performance of the aforementioned methods is compared in a relatively low signal-tonoise ratio(SNR)environment.Simulation conditions are the same with those of Example 1.In addition,received signals obtained by the two UAVs are contaminated by the zero-mean white Gaussian noise and the SNRs are both-10dB.For fair comparison,the scope of FDOA and TDOA are set to be the same.However,the TDOA scope of FRT-SFT method will be shrunk to half due to the frequencyreversing operation.The estimation results are presented in Fig.10.

Fig.10(a) shows the demodulation result of (13).The cluttered image shows that the signal is submerged in noise.Fig.10(b)gives the estimation result of CAF.It is obvious that the CAF,which adopts the narrowband signal model and ignores the range migration,cannot obtain the TDOA and FDOA.The constant delay defined FRTSFT method loses much signal energy when performing correlation operation.Hence,it no longer works in low SNR cases,as shown in Fig.10(c).The FASF-SFT method presented in Fig.10(d)seems to be able to achieve parameter estimation.Unfortunately,the coarse resolution and inaccurate result reveals its inferior performance.Fig.10(e) gives the result of MLE,which achieve the optimal performance under white Gaussian noise through 2D brute-force searching.Taking the MLE as a benchmark,the proposed method also achieves satisfactory estimation performance,as shown in Fig.10(f).Moreover,the resolution of the proposed method is much better than that of FASF-SFT,which also corresponds to higher estimation accuracy.

5.2.Anti-noise performance

The anti-noise performance of the above methods is investigated in this part.Similar to subsection 5.1,the SNRs for both UAV signals are the same,which change from-20dB to 10 dB with 1 dB interval.For each SNR value,500 times independent Monte Carlo trials are performed.Other simulation parameters are the same with Example 1.The root mean square errors (RMSEs) are used to evaluate the performance of TDOA and FDOA estimations.Fig.11 plots the performance curves.

From the comparison results in Fig.11(a) and (b),we can find that the proposed method has almost optimal anti-noise performance.However,the computational complexity is much lower than that of MLE.The SNR threshold of FASF-SFT is about 4 dB higher than the proposed method.The reason is the bilinear autocorrelation of range frequency introduces interference between signal and noise.Therefore,this method will lose its estimation ability under low SNR conditions.In addition,the estimation accuracy of FASF-SFT is inferior due to the coarse FDOA resolution,which is consistent with the result in Fig.10(d).The CAF uses a narrowband model and ignores the migration.Hence,the signal energy will spread over several TDOA and FDOA resolution bins.From the curves we could find,it suffers more performance loss and inaccurate estimation results.As to the FRT-SFT,the frequency reversing transform employs the autocorrelation with constant delay,which accumulates much less signal energy than FSAF-SFT [19].Consequently,it has the worst performance.

Overall,based on the analysis above,we may easily conclude that the proposed method could achieve nearly optimal estimation performance with much lower computational cost,and outperforms the other representative methods.

6.Conclusions

This paper studies the problem of TDOA/FDOA estimation using UAVs in passive cooperative localization application.A robust parameter estimation method based on interpolation and resampling is proposed.The method introduces the coherent integration framework of active radar for multiple pulses and solves the problem of TDOA time-varying and Doppler ambiguity.Under the constraints of no synchronization error,accurate UAV location,and white Gaussian noise environment,nearly optimal estimation accuracy and anti-noise performance are obtained.Besides,an efficient implementation based on non-uniform fast Fourier transform is derived to decrease the computational complexity.The highlights of the proposed method include the followings.

(a) The slow time interpolation is performed to extend the Doppler scope.In this way,the unambiguous Doppler frequency can be observed.

(b) The resampling operation is introduced to eliminate the coupling between range frequency and slow time.

(c) The IDFT of different range frequency bins is performed to coherently integrate the signal energy and suppress the grating lobes caused by interpolation.

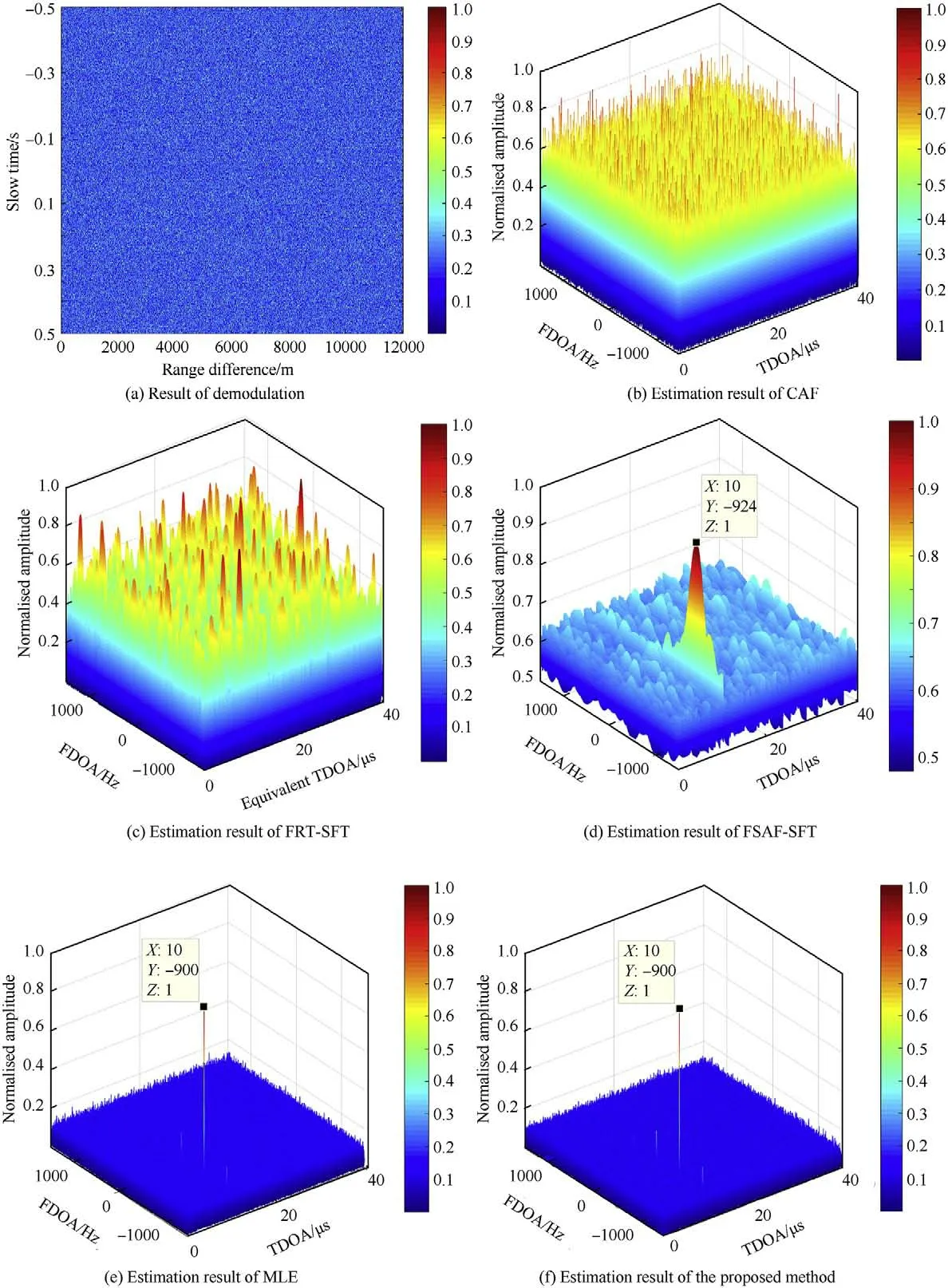
Fig.10. Estimation performance of different methods.

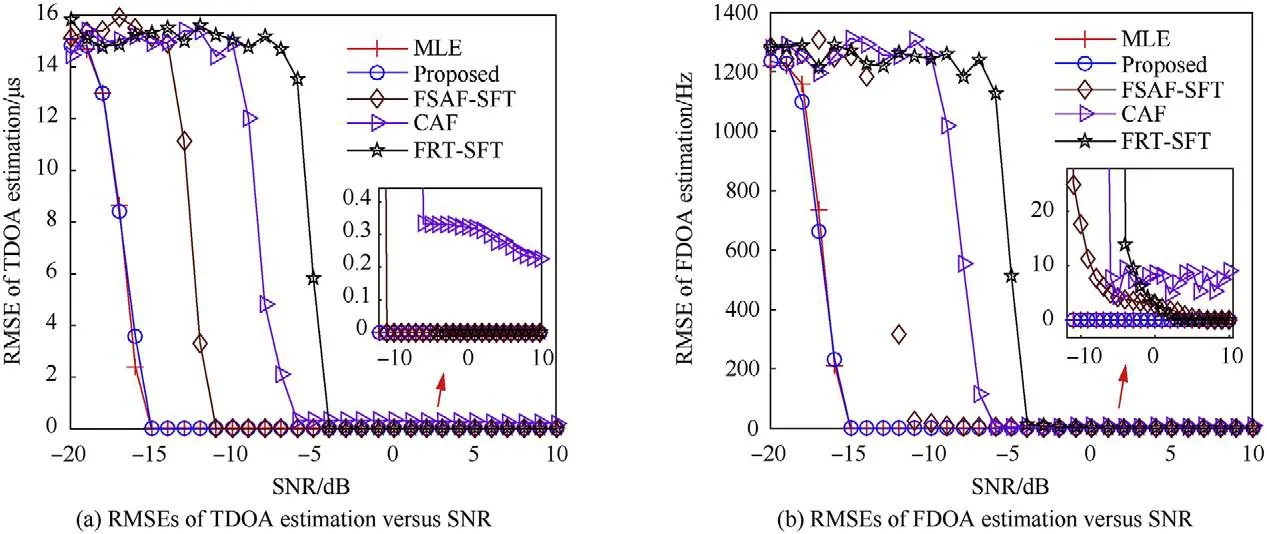
Fig.11. Anti-noise performance comparison.

(d) Compared with MLE,the proposed method can be fast implemented via complex multiplications,FFT and IFFT,which is beneficial to practical applications.

The above constraints will inevitably degrade parameter estimation performance and localization accuracy.Therefore,future works might consider passive localization when UAV location errors or synchronization errors occur.Correspondingly,signal model and coherent integration method should be re-derived.The expected performance will also be compared with peer methods.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors would like to acknowledge National Natural Science Foundation of China (Grant No.xxxxxx).