Driving force coordinated control of an 8×8 in-wheel motor drive vehicle with tire-road friction coefficient identification

Zheng Zhang,Chun-guang Liu,Xiao-jun Ma,Yun-yin Zhang,Lu-ming Chen

Department of Weapons and Control Engineering,Army Academy of Armored Forces,Beijing,100072,China

Keywords:In-wheel motor Tire-road friction coefficient Slip ratio Sliding mode control Conditional integrator Acceleration slip regulation

ABSTRACT Because of the complexities of tire-road interaction,the wheels of a multi-wheel distributed electric drive vehicle can easily slip under certain working conditions.As wheel slip affects the dynamic performance and stability of the vehicle,it is crucial to control it and coordinate the driving force.With this aim,this paper presents a driving force coordination control strategy with road identification for eightwheeled electric vehicles equipped with an in-wheel motor for each wheel.In the proposed control strategy,the road identification module estimates tire-road forces using an unscented Kalman filter algorithm and recognizes the road adhesion coefficient by employing the recursive least-square method.According to road identification,the optimal slip ratio under the current driving condition is obtained,and a controller based on sliding mode control with a conditional integrator uses this value for acceleration slip regulation.The anti-slip controller obtains the adjusting torque,which is integrated with the driver-command-based feedforward control torque to implement driving force coordination control.The results of hardware-in-loop simulation show that this control strategy can accurately estimate tire-road forces as well as the friction coefficient,and thus,can effectively fulfill the purpose of driving force coordinated control under different driving conditions.

1.Introduction

Acceleration slip regulation (ASR) system is used to reduce significant wheel slip under complex road environments and driving conditions,and thereby,improve driving safety [1,2].Traditional fossil fuel vehicles mainly realize anti-slip control by means of reducing the driving speed,controlling the engine torque output,changing the gear ratio of the transmission system,and triggering the braking system to realize wheel slip ratio control.However,these methods impart obvious physical forces on the vehicle when activated,which affects vehicle ride comfort [3,4].Compared with traditional vehicles,electric vehicles(EVs)with inwheel motors can directly control the torque output of each motor to achieve a state of wheel slip control,which can make it easier to design driving force control systems for improving EV dynamic performance and steering stability [5].

Based on previous studies,researchers have proposed various driving force control systems for in-wheel motor drive vehicles[6-15].Wheel slip state is directly determined based on the wheel slip ratio;therefore,most ASR systems are designed on the basis of slip ratio control methods.A nonlinear control system has been introduced by Majdoub et al.[16];in their proposed system,global asymptotic stability is ensured by adjusting the wheel slip and acceleration.An ASR system based on model predictive control(MPC) has also been described by Yuan et al.[17];their proposed system controls the slip ratio of each wheel within a certain range to prevent wheel slip.Additionally,to improve the precision of driving torque control,a method based on a sliding mode control(SMC) algorithm has been presented by Kuntanapreeda [18].According to the single-wheel force model of the vehicle and the sliding mode function,the algorithm deduces the equivalent control amount of motor output torque to implement wheel anti-slip control.

In the presented studies,the proposed driving force controllers were designed for civilian EVs with four in-wheel motors.They can adapt only to a single road environment,without considering the adaptability of the controller to variations in road surface type.However,the road conditions of EVs with multiple in-wheel motors often have sudden changes,and sometimes they are faced with special situations such as fast acceleration and off-road driving.Therefore,it is necessary to assess different road conditions,and to coordinate the driving force accordingly.

Assessing different road conditions requires performing road identification,i.e.,identification of the road adhesion coefficient[19].Road identification methods are usually classified into two categories:test-based and model-based [20-25].Test-based methods typically exhibit high precision under good test conditions.However,the reliability of the employed optical and acoustic sensors is easily affected by driving conditions and the external environment.Furthermore,strict requirements pertain to the selection of information collected by the sensors.Model-based methods,including the slip slope model and tire model,depend on the relationship between slip ratio and road adhesion coefficient.Because of the complexities of actual driving conditions,many factors can affect the calculation accuracy of the slip ratio;hence,those algorithms need to avoid the influence of external uncertainty.

This paper presents a new driving force coordination control system with road identification for EVs equipped with multiple inwheel motors.The system design relies on more complete vehicle modeling,which fully considers tire-road interaction.The issue of road identification is revisited,i.e.,an unscented Kalman filter(UKF) is used to estimate tire forces,and then,the recursive least square (RLS) method is adopted to calculate the road adhesion coefficient.Furthermore,a controller based on sliding mode control with a conditional integrator(SMC&CI)is implemented for ASR,so that the vehicle can have an improved dynamic performance and stability even if the road conditions change.Finally,the hardwarein-loop simulation (HILS) platform was introduced to test the performance of the control system under typical driving conditions.

2.Vehicle dynamics model

In this study,the driving force coordinated control for different road and working conditions was investigated for an EV with eight wheels (Fig.1).The nonlinear vehicle model was established by ignoring air resistance and linearizing rolling resistance.Additionally,forces applied to the wheels were analyzed (Fig.2).

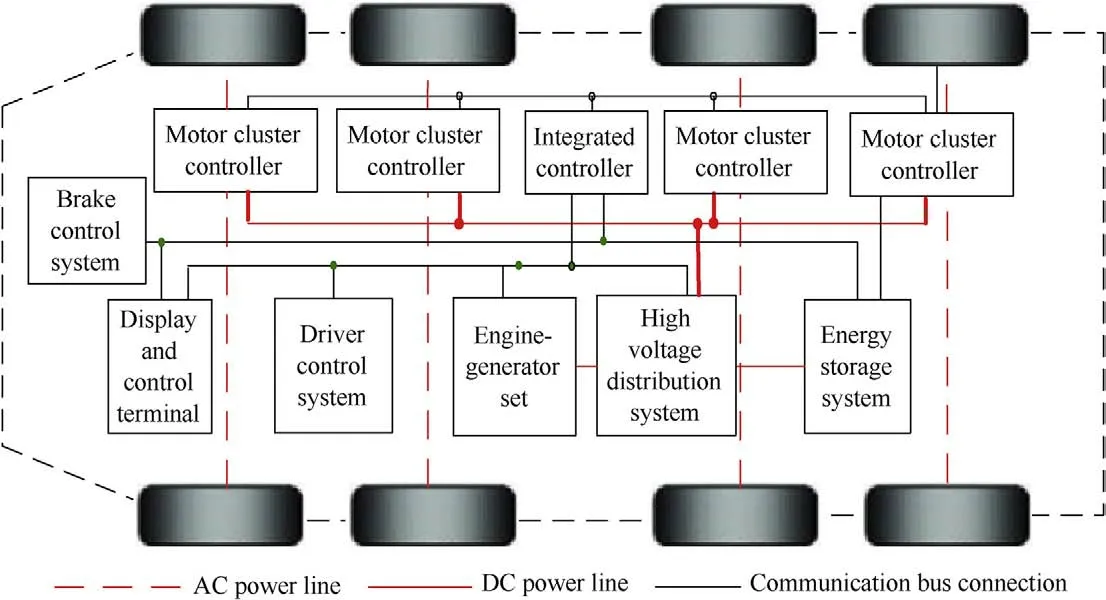
Fig.1. Structure of EV with eight in-wheel motors.

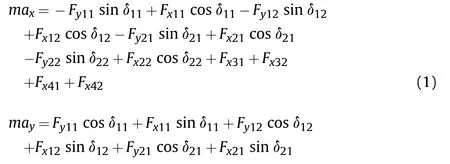
Fig.2. Wheel force analysis.

In accordance with Newton’s laws of motion and the principles of vehicle dynamics,the longitudinal and yaw movements of the vehicle are respectively expressed by

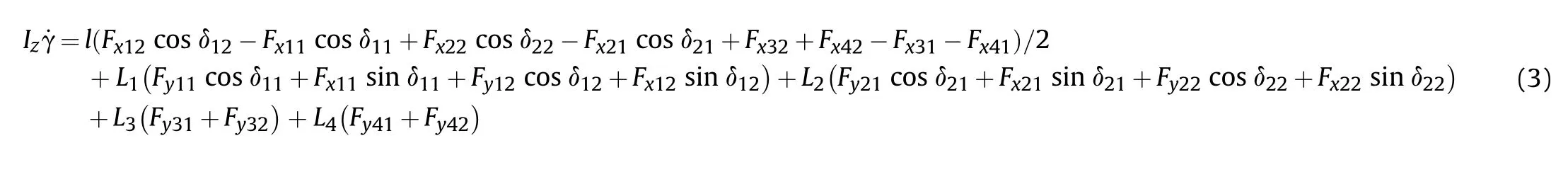
where γ represents the yaw rate of the vehicle;ais longitudinal acceleration;ais lateral acceleration;Iis the yaw mass moment of inertia;m denotes the vehicle mass;Lis the distance between the i-th axis and the center of gravity(CG);and l is the track width.Fand Fare the longitudinal and lateral forces of the wheels,respectively.The subscript i∈（1，2，3，4）represents the i-th axis of the vehicle;j∈（1，2，3，4）represents the left and right wheels of the vehicle;and δrepresents the steering angles of the wheels.

The wheel rotation motion is described by

where Mis the rolling resistance moment

The driving torque Tcan be calculated as

where I and ω are the moment of inertia and angular velocity of the wheel,respectively;V and R denote wheel speed and radius,respectively;fdenotes rolling resistance coefficient;Fdenotes the vertical load;Tis motor output torque;and iis the transmission ratio of the reducer.

Change in the characteristics of the tires will affect the motion characteristics of the vehicle;therefore,the key to further investigating the relationship between wheel forces and vehicle motion is to establish a reasonable and accurate tire model.Considering that the Dugoff tire model has good theoretical boundaries,fast calculation speed,and high simulation accuracy,and can be used to describe the motion characteristics of vehicles under extreme conditions better than other tire models,it was selected in this study to calculate the tire force.

The forces of the wheel are expressed as

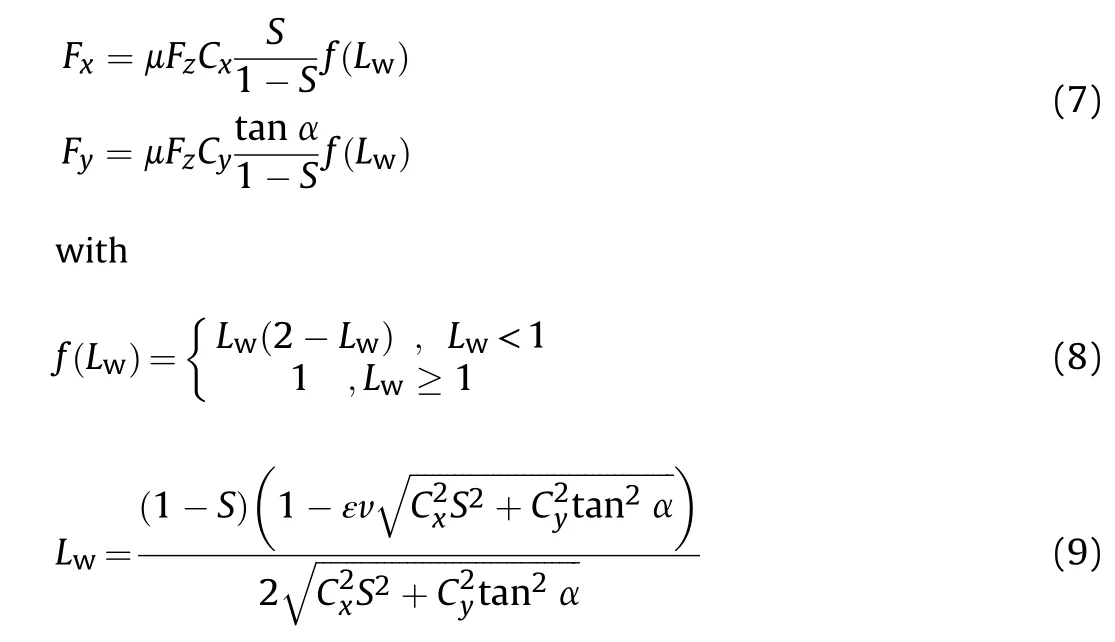
where Lis a boundary value that represents the nonlinear characteristic of the tire force,and ε is the velocity influence factor.S is the actual wheel slip ratio,α denotes the wheel sideslip angle,and μ denotes the road friction coefficient.

In-wheel motors of EV in this study must meet important requirements such as high torque,power factor,and density efficiency;hence,a permanent magnet synchronous motor(PMSM)is used (Table 1).

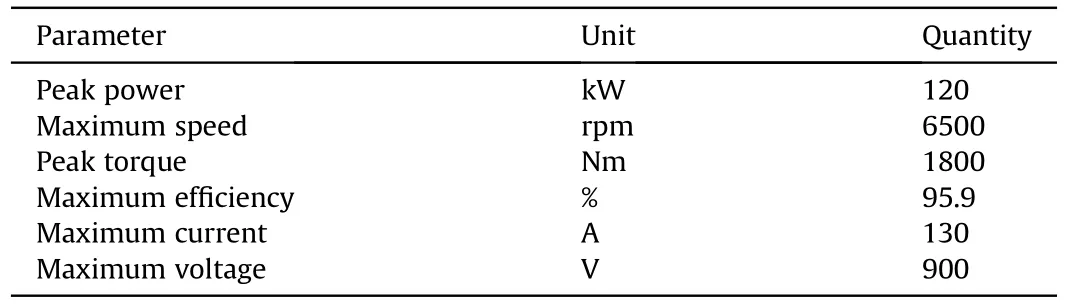
Table 1 Main design parameters of in-wheel motors.

The in-wheel motor features direct torque control,which has the main task of providing each wheel with the torque required by the driving force coordination control system,which can be simplified as

where τ is the motor time constant for describing the response speed of the motor;Tis motor torque command;and s is a complex variable.According to a bench test,a τ value of 0.005 was used in this study.

3.Design of the road identification system

Considering the different driving requirements under various road conditions analyzed in this study,UKF with an RLS method was used for road identification.Specifically,the UKF method was used to assess the tire force,then the road adhesion coefficient was obtained by using the RLS method.

3.1.Tire force estimation

The state-space representations are constructed from Eqs.(1)-(6),namely

where X,U,and Y denote the state vector,input vector,andmeasurement vector,respectively;w(t) and v(t) are the process noise and measurement noise,respectively.

The state vector X can be written as

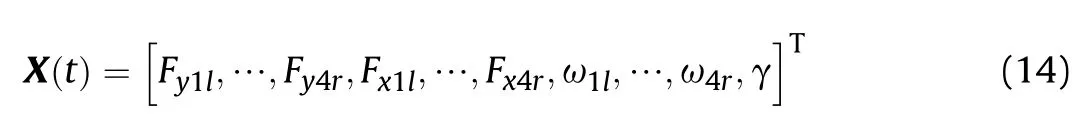
The input vector U consists of the steering angle of the front two axles,vertical load,and driving torque of each wheel.

The measurement vector Y can be expressed as

The vehicle central controller needs discrete algorithm when the vehicle is running,so the calculation step and output information should be discrete sequence.Eq.(7) is discretized as

where k and k+1 are the discrete sampling times.

To describe the system states,the filter performs the unscented transformation of the state vector and creates 2n+1 sigma points,which are expressed as

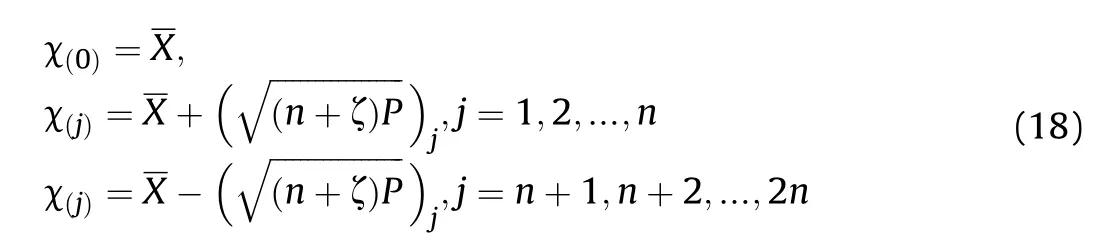
The corresponding weights of the sigma points are

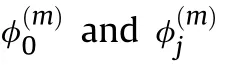
The initial conditions are set as

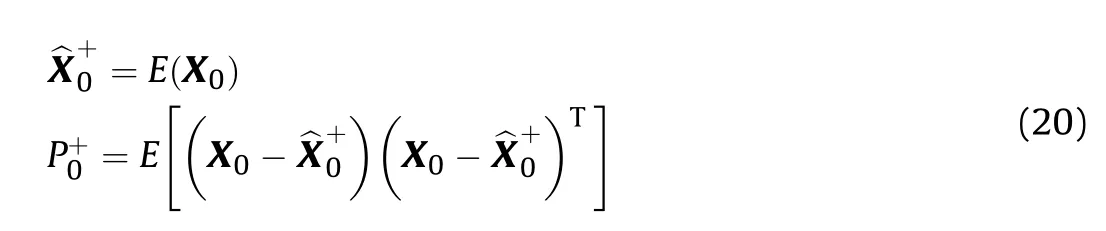
The predicted values of sigma points are obtained by unscented transformation of the state vector:

3.2.Estimation of tire-road friction coefficient using the RLS methodology

The RLS method is unbiased,effective,and easily computable,consisting of the following steps.

The tire force measurement value z should be estimated according to the UKF algorithm:

where f[k，μ]refers to the expression of the Dugoff tire model and vis random noise.

Subsequently,z（k）can be linearized,and approximately expressed as

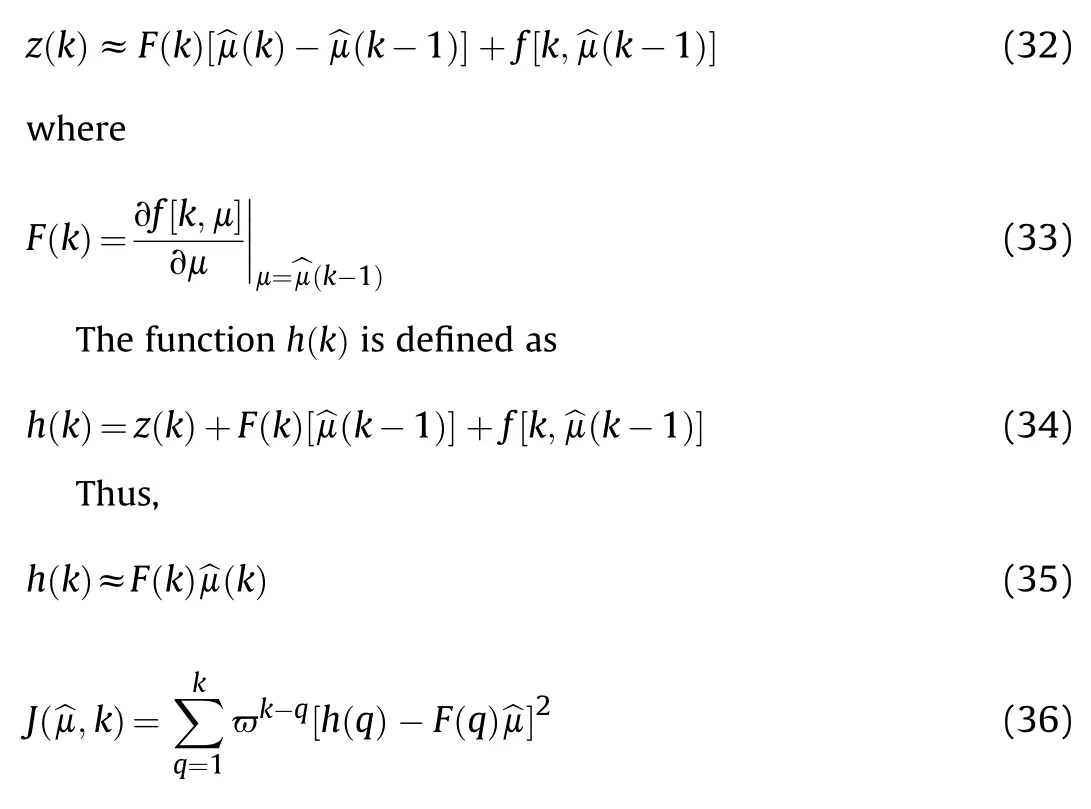
where J（.）is the value function;ϖ represents the forgetting factor.

According to the principle of minimization of the value function,the expression of the least-square method is obtained as

The error covariance matrix of Eq.(36) is

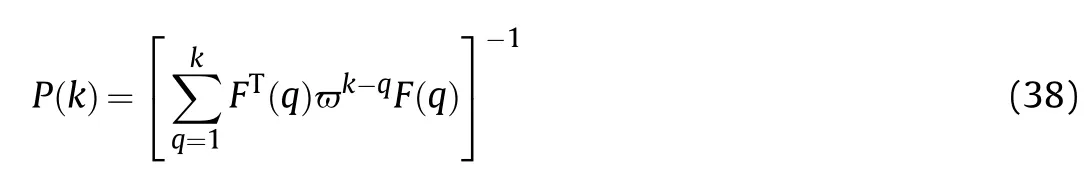
According to the Sherman-Morrison equation,recursive calculation is carried out as

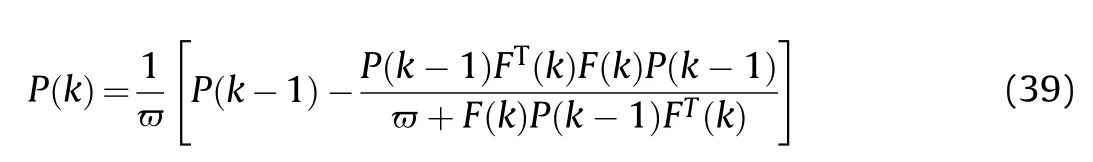
Substituting Eqs.(37)and(38)into Eq.(36),the specific iterative process is formulated as

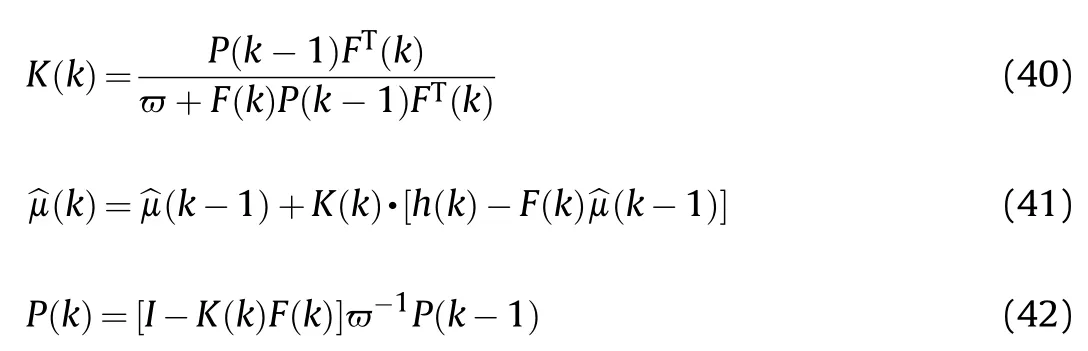
To minimize the estimation error under such conditions,the threshold of the slip ratio is set to S=8%,so that the estimation result of the RLS method is updated normally only when S ＞S,whereas in the case of S ≤Sthe estimation value is taken according to the previous time.

Thus,the following expression is obtained:

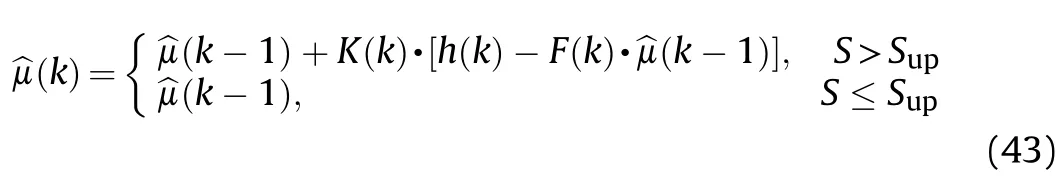
4.Design of the driving force coordination control system

To enhance the practicability of the control system,a modular hierarchical driving force coordination control structure is proposed,Fig.3.According to the vehicle driving state information,the road identification module calculates the road adhesion coefficient in real time;then,the optimal wheel slip ratio under the current driving condition is obtained.

4.1.Design of the controller based on SMC&CI for ASR

For EVs with in-wheel motors,when the road surface is wet and slippery,some driving operations are likely to cause significant wheel slip,which affects the vehicle dynamics and its safe performance.When the vehicle is driving,the optimal slip ratio corresponding to the road surface with a high adhesion coefficient is also large.If the optimal slip ratio of the road surface could be known,it would be very conducive for the design of the ASR system of an EV with in wheel motors.Therefore,for this study,based on the model discussed in Section 3.2,the optimal wheel slip ratio was obtained with a lookup table according to the estimated road adhesion coefficient.

The advantages of SMC are its simple principle and easy calculation and implementation;therefore,this method is often used in wheel slip ratio control.To avoid jitter in the control signal caused by discontinuities near the sliding surface,herein,we improved the traditional SMC algorithm and the design of the ASR system with a controller based on SMC&CI is discussed in this section.The specific calculation steps are as follows.

The slip ratio difference is defined as

where Sis the optimal slip ratio.

Taking the derivative of Eq.(44) yields

By adopting the constant speed approach rate,the sliding surface of the SMC controller is written as

where kγ refers to the approach rate,and kγ ＞0.

Although the SMC algorithm improves the system robustness,the discontinuous characteristics near the sliding mode surface lead to serious control signal jitter.To reduce the chatter and integral saturation problems near the sliding surface,the conditional integrator is introduced by adopting the notion of “integral separation,” to further improve the control algorithm,design the controller based on SMC&CI,and improve the system response characteristics and control effect.

Based on Eq.(44),the conditional integral term is added as

Fig.3. Structure of the driving force coordinated control system.

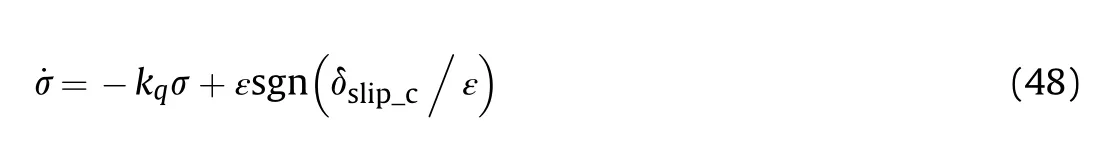
where δis the newly added sliding surface,and δ（e，σ）=0;σ is the error integral,with σ（0）≤ε/k;kis the conditional integral adjustment parameters,with k＞0;and ε is the width of the sliding mode switching boundary layer,with ε ＞0.

Replacing sgn（δ/ε）with a saturation function sat（δ/ε）yields

By combining the motion equation of the EV with in-wheel motors and the motor model,the adjusting torque of the controller can be obtained.

The Lyapunov functions are defined as

Using the specific certification process of system stability described in Ref.[26],the stability of the system is proved.

4.2.ASR activation condition

Within the driving force coordination control system (Fig.3),according to the vehicle driving state information,the road identification module calculates the road adhesion coefficient in real time;then,the optimal wheel slip ratio under the current driving conditions can be obtained.With this system,on the one hand,the controller based on SMC&CI in the ASR system prevents the wheel from excessive slip and obtains the corresponding adjusting torque.On the other hand,the driving state judgment module is actuated to determine whether the adjusting torque from the controller based on SMC&CI is effective in the current working state,so as to obtain the modified adjusting torque.Subsequently,the modified adjusting torque is integrated with the feedforward control torque to obtain the demand torque required for vehicle driving.Finally,the driving demand torque is distributed to the actuators,and the torque distribution information is fed back to the vehicle model to form a complete control strategy.

The interaction between the ASR system and driver’s command needs to be considered when driving force coordination control is carried out for an electric-drive vehicle.In the case of serious wheel slip,ASR can be actuated to improve the vehicle handling stability.However,in non-acceleration conditions (such as deceleration or low-speed cruising),ASR intervention tends to cause adverse interference with the vehicle integrated control system.For the vehicle in this study,it tends to face various complex driving conditions,so it is necessary to set mode judgment to determine whether ASR should take effect.Therefore,ξis introduced as a control parameter to represent the working/exiting state of ASR,i.e.,when ASR works normally,ξis set to 1;when the accelerator pedal opening index ρ is less than 0.2 or its change rate is negative,ASR should be in the exit state,so ξis set to 0.

Considering that the operators of EVs with in-wheel motors are the input interface of the driving signal,ρ is defined as

where ε,ε,and εdenote the empty stroke,effective stroke,and maximum stroke of the accelerator pedal,respectively.

After judging the intervention conditions,the modified adjusting torque of ASR is expressed as

where Tis the adjusting torque from the controller based on SMC&CI.

Thus,the target torque output by the drive force coordination control system is computed as

where T（n）is the maximum torque corresponding to rotation speed n.

5.Hardware-in-loop simulation and analysis

Any driving force coordination control system needs to demonstrate excellent real-time performance and reliability.It should be able to quickly respond to the dynamic operation of the driver and real-time changes in vehicle state,calculate the control instructions,and send them to the actuators in real time.Owing to the complex structure and large weight and volume of the research object,it is necessary to minimize the safety risk and the research and development cost of the sample vehicle test;therefore,in this study,the real-time testing of the corresponding working conditions was conducted with the help of the hardware-in-loop simulation (HILS) platform.

The HILS platform was composed of host computers,a dSPACE(dSPACE Company) workstation,integrated controller,two RT-LAB(OPAL-RT Technologies) workstations,a Vortex (CM-LABS) simulation workstation,and the simulated driving system.To observe the vehicle operation scene and key simulation data during simulation,the upper computer corresponding to all simulation nodes was displayed in a centralized way at the same time by using a multi-screen display wall.In addition,according to the characteristics of all kinds of equipment,we specially customized a suitable stand to place the equipment,which simplified both the operation of the hardware-in-loop test and to the data observation (Fig.4).

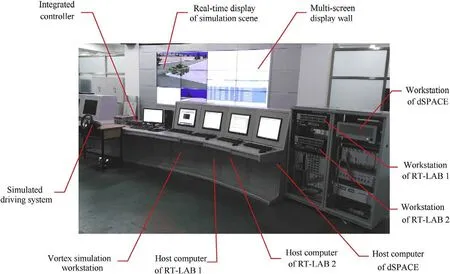
Fig.4. Overall structure of the simulation platform.

The control system was designed to effectively identify the current driving road information,and to coordinate the driving force of the vehicle with ASR as the core.Therefore,the simulation verification was carried out with three typical road conditions,namely low-adhesion road,μ-split road,and docking road.

We also designed a widely used SMC-based controller for ASR as a comparison of the proposed driving force coordination control system.The SMC-based ASR system,as the comparison,does not have the function of road identification.Considering that 8×8 inwheel motor drive vehicles are more likely to slip when driving on low adhesion roads,the comparison system uses a single optimal slip ratio(0.13) to achieve vehicle anti-slip control.

In the following cases,we compared the maneuverability and handling stability of a vehicle without driving force control,a vehicle controlled by the SMC-based ASR system with a fixed optimal slip ratio,and a vehicle controlled by driving force coordination based on road surface identification.

5.1.Low-adhesion road driving simulation

The road conditions were simulated as a slippery road(μ=0.2),whereas the experimental conditions were designed to start at an initial speed of 0 km/h,and then accelerate along the road in a straight line.The initial values of steering wheel and wheel slip were δ(0)=0 and S(0)=0,respectively.

Because a large number of studies are based on a tire model that fits the μ-S curves of typical roads (such as dry asphalt,dry concrete,and icy and snowy road),a typical-road database was established,and a fuzzy logic method was used to compare the characteristics of the current road and with those of typical roads,so as to estimate the adhesion coefficient of the road.In this study,the fuzzy logic estimation method (hereinafter,“the fuzzy method”)was used as a comparison for the proposed road adhesion coefficient estimation method (hereinafter,“the RLS method”).

To evaluate the estimation method quantitatively,several commonly used statistical error indexes were adopted to represent the error between the estimated road adhesion coefficient and the actual value set by simulation.

The maximum error can be expressed as

The expression of mean absolute error is

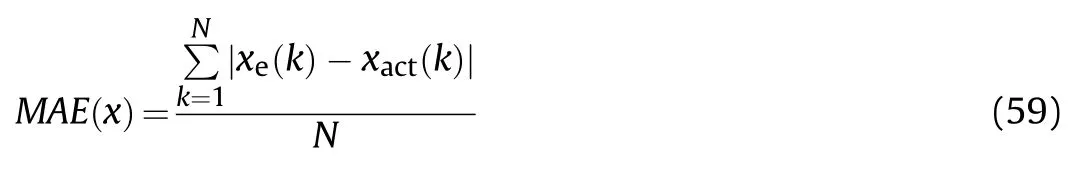
The root mean square error is

where N is the number of samples;x（k）and x（k）are the estimated value and the actual value of the k-time state parameters.

For the slippery road condition,both the fuzzy and RLS methods were used to estimate the road adhesion coefficient.However,compared with the RLS method,the deviation between the value estimated by the fuzzy method and the actual value is larger.According to the statistical data (Fig.5 and Table 2),the RLS method has better estimation accuracy than the fuzzy method.

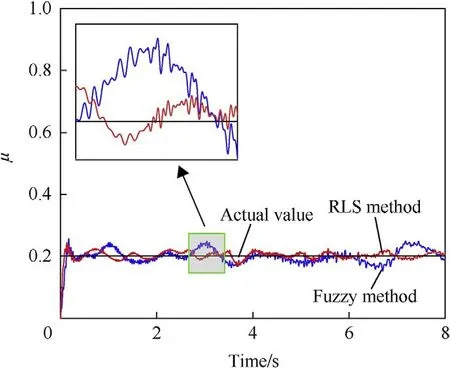
Fig.5. Estimation of road adhesion coefficient for low-adhesion road simulation.

Table 2 Statistics of estimation error of road adhesion coefficient for low-adhesion road simulation.

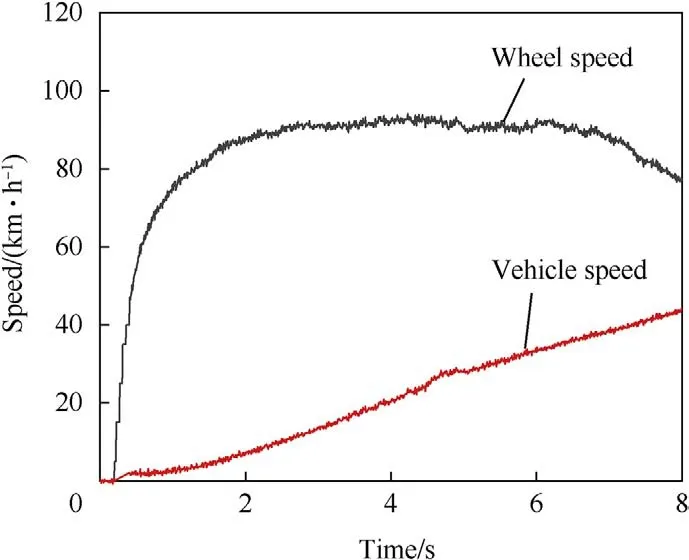
Fig.6. Vehicle speed and wheel speed when starting and accelerating on a lowadhesion road without driving force control.

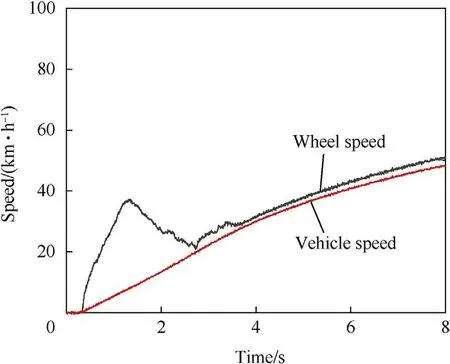
Fig.7. Vehicle speed and wheel speed when starting and accelerating on a lowadhesion road with the SMC-based ASR system.

In the simulation,the left wheel of the first axle was taken as the observation object,and its wheel edge speed and slip ratio were recorded.According to the vehicle speed and wheel speed curves(Figs.6-8),when the driving force control was not applied on the vehicle,the tires slipped significantly,and the wheel edge speed increased rapidly,in strong contrast to the vehicle speed.However,applying the SMC-based ASR system reduced excessive wheel slip,and the difference between wheel edge speed and vehicle speed decreased.After the driving force coordination control was applied,wheel slip was clearly restrained during the entire movement process,and the difference between the wheel edge speed and vehicle speed improved over that of the SMC-based ASR system.These results indicate that the proposed driving force coordination control system can improve the driving performance.

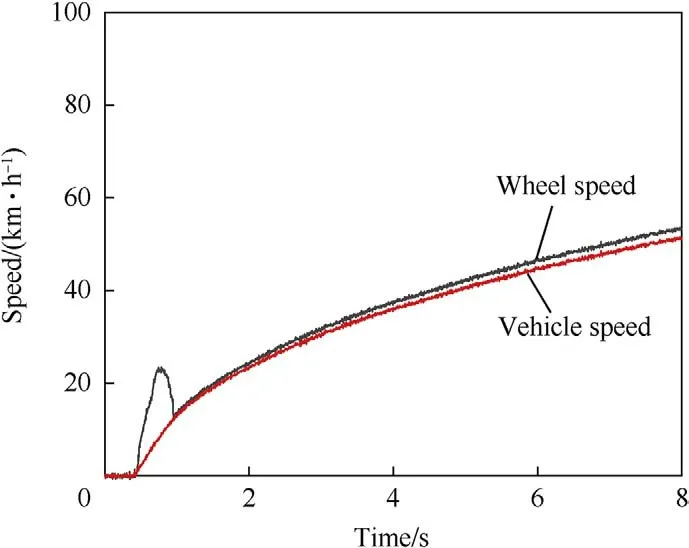
Fig.8. Vehicle speed and wheel speed when starting and accelerating on a lowadhesion road with driving force coordinated control.

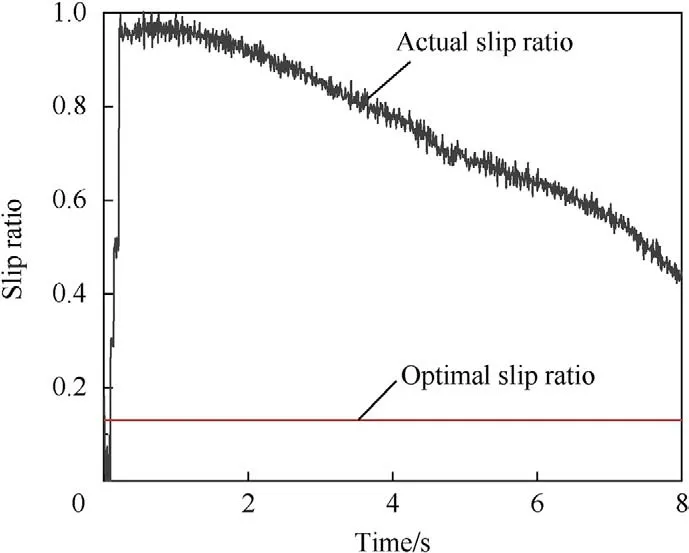
Fig.9. Wheel slip ratio of the vehicle starting and accelerating on a low-adhesion road without driving force control.

It was observed that when the vehicle was not under driving force control,there was a large difference between the actual wheel slip ratio and the optimal wheel slip ratio for that road condition.The maximum error between the actual wheel slip ratio and the optimum wheel slip ratio was approximately 79%,which strongly affects the dynamic performance and stability performance of driving(Fig.9).Applying the SMC-based system adjusted the actual wheel slip ratio when the wheel slipped,making the actual tire slip ratio fluctuate near the optimal slip ratio.However,a chattering phenomenon is observed,which degrades the control effect(Fig.10).For the vehicle with driving force coordinated control,when the wheel slipped,the controller based on SMC&CI effectively adjusted the torque of the in-wheel motors,which brought the actual slip ratio closer to the optimum.In addition,the proposed driving force coordination control system effectively improved the chattering problem of the traditional SMC-based controller,and the control effect was clearly observable (Fig.11).

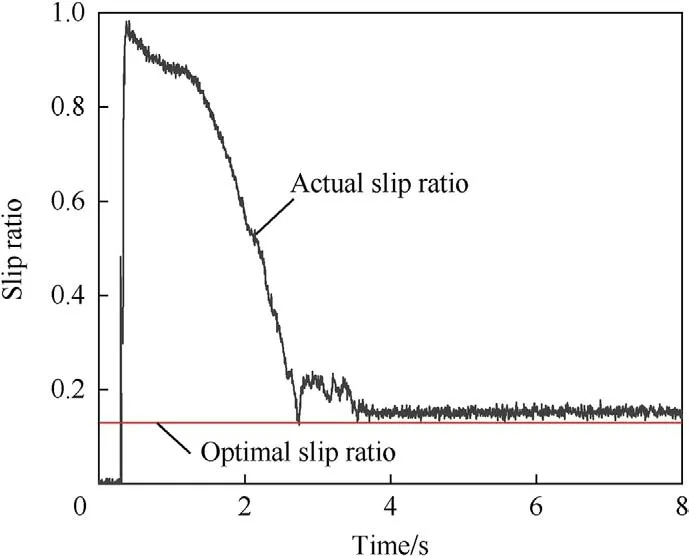
Fig.10. Wheel slip ratio of the vehicle starting and accelerating on a low-adhesion road with the SMC-based ASR system.

Fig.11. Wheel slip ratio of the vehicle starting and accelerating on a low-adhesion road with driving force coordinated control.

5.2.The μ-split road driving simulation

In this simulation,the road was set under μ-split conditions.On the left and right sides of the vehicle,the tire-road adhesion coefficients were μ=0.2 and 0.8,respectively.The experimental conditions were designed to start at an initial speed of 0,and then accelerate along the road in a straight line.The initial values of steering wheel and wheel slip were δ(0)=0 and S(0)=0,respectively.The left and right wheels of the first axle were taken as the observation objects to record the wheel speed and slip ratio.

Both methods identified the μ-split road,but as a general trend,the estimated value of the RLS method was closer to the actual value than that of the fuzzy method.The comparison(Figs.12 and 13 and Table 3) indicates that the RLS method is more accurate.

Fig.12. Estimation of road adhesion coefficient of the left side for the μ-split road simulation.

Fig.13. Estimation of road adhesion coefficient of the right side for the μ-split road simulation.

Table 3 Statistics of adhesion coefficient estimation error for the μ-split road simulation.

Comparing the wheel edge speed and vehicle speed shows that the wheel edge speed of the vehicle without driving force control is quite different on both sides.On the one hand,the left wheel drove on the low-adhesion side,and the wheel edge speed of the left wheel deviated significantly from the vehicle speed.On the other hand,the right wheel drove on a relatively good road surface;the slip phenomenon was relatively mild,and the wheel edge speed of the right wheel tracked the vehicle speed closely (Fig.14).

After applying the SMC-based ASR system,the difference between the wheel edge speeds of both sides was reduced,and the wheel edge speed tracked the vehicle speed closely;however,this control system does not control according to the road conditions on each side (Fig.15).In contrast,the driving force coordination control system obviously adjusts the wheel edge speed of each side according to the road identification.Hence,the driving force coordination control system was shown to be more effective than the SMC-based ASR system(Fig.16).

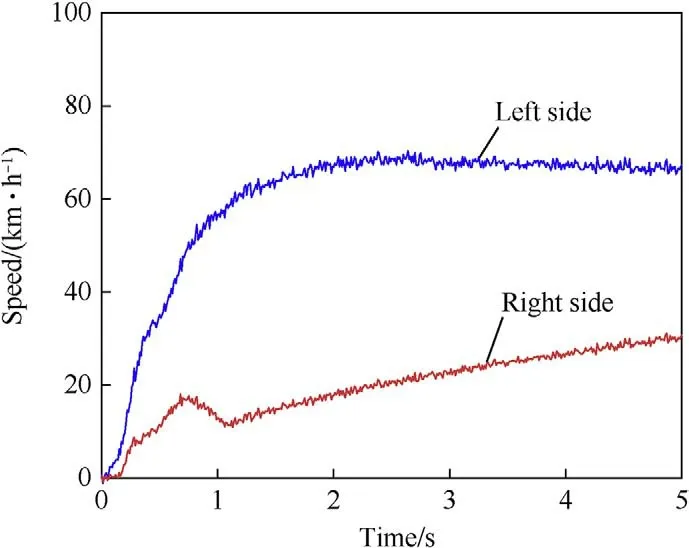
Fig.14. Wheel speed of the left side and right side when starting and accelerating on a μ-split road without driving force control.

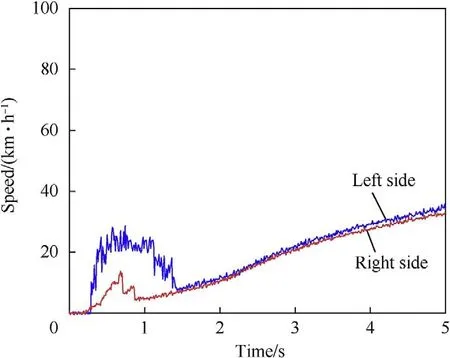
Fig.15. Wheel speed of the left side and right side when starting and accelerating on a μ-split road with the SMC-based ASR system.

For the vehicle without driving force control,there was a large difference between the actual slip ratio of the left and right sides.For the left side,with a low road-adhesion coefficient,the actual slip ratio was significantly higher than the optimum.For the right side,with a high road-adhesion coefficient,although the real wheel slipped at the beginning,the deviation between the actual wheel slip ratio and the optimum was small in the overall trend(Fig.17).When the SMC-based ASR system was applied,the wheel slip on both sides was restrained to some extent,but the fluctuation was large,the control effect was not very stable,and the slip rate of the wheels on both sides could not be adjusted separately according to the different road-adhesion coefficients (Fig.18).However,during the entire driving process,the driving force coordination control system identified the difference in adhesion coefficient of the μsplit road,effectively restrained the excessive wheel slip,reasonably reduced the deviation between the actual slip ratio on both sides and the corresponding optimal slip ratio according to the road conditions,and improved the driving ability of the vehicle.The dynamic parameters of the vehicle with the driving force coordination control system fluctuated less,indicating an improved driving control effect (Fig.19).

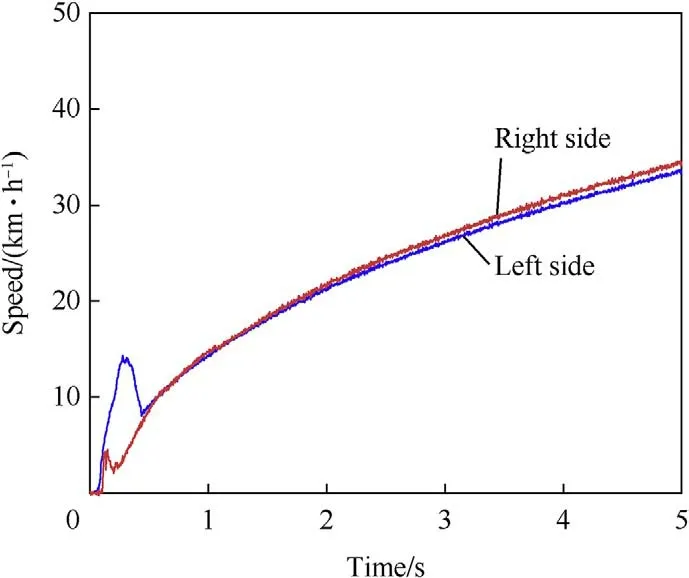
Fig.16. Wheel speed of left side and right side when starting and accelerating on a μsplit road with driving force coordinated control.

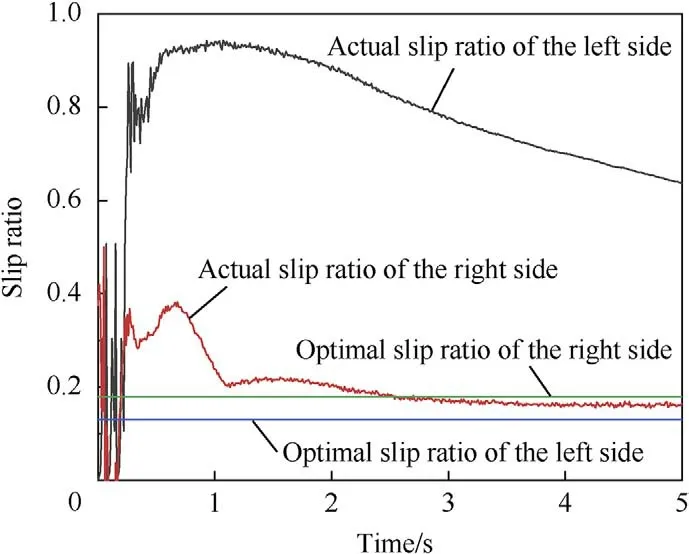
Fig.17. Wheel slip ratio of the vehicle starting and accelerating on a μ-split road without driving force control.

When the vehicle accelerated on the μ-split road,the maximum yaw rate of the vehicle without driving force control reached approximately 11 mrad/s,and the lateral displacement continued to increase to 2.49 m.The vehicle exhibited the track deviation phenomenon,and it was clearly out of control.Compared with the vehicle without driving force control,the ASR system based on SMC and driving force coordination control exhibited good control on the vehicle instability.The vehicle yaw rate and lateral displacement were reduced.The maximum yaw rate and lateral displacement of the vehicle with the ASR system based on SMC were approximately 7 mrad/s and 1.23 m,respectively.The maximum yaw rate of the vehicle with the driving force coordinated control system was less than 0.005 rad/s,and the lateral displacement was controlled well,with a maximum value smaller than 0.5 m.The proposed driving force coordinated control system exhibited smaller jitter and better stability (Figs.20 and 21).

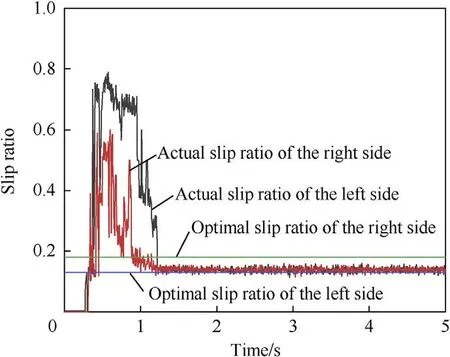
Fig.18. Wheel slip ratio of the vehicle starting and accelerating on a μ-split road with the SMC-based ASR system.

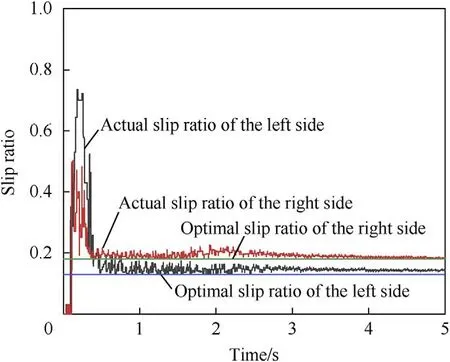
Fig.19. Wheel slip ratio of the vehicle starting and accelerating on a μ-split road with driving force coordinated control.

5.3.Docking road driving simulation

In this simulation,road conditions were set to a docking road with a variable coefficient of adhesion,namely,first 5 s driving on a low-adhesion road (μ=0.2),and the last 5 s driving on a highadhesion road (μ=0.8).The experimental conditions were designed to start at the initial speed of 10 km/h,and then accelerate along the road in a straight line.The initial values of steering wheel and wheel slip were δ(0)=0 and S(0)=0,respectively.

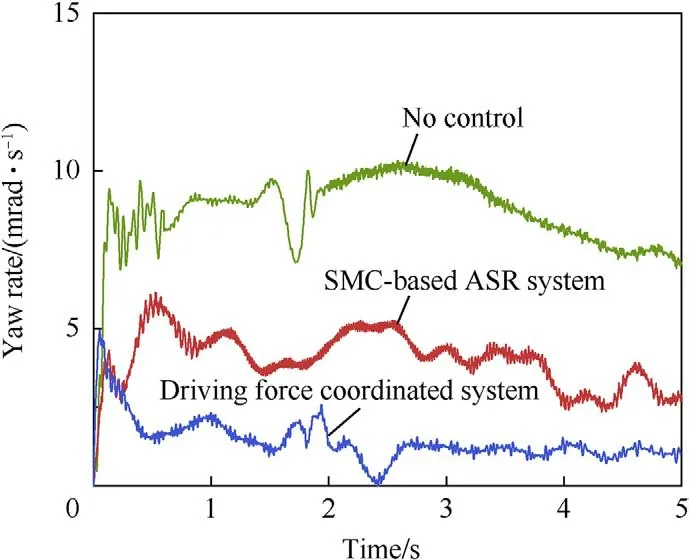
Fig.20. Yaw rate of vehicle starting and accelerating on a μ-split road.

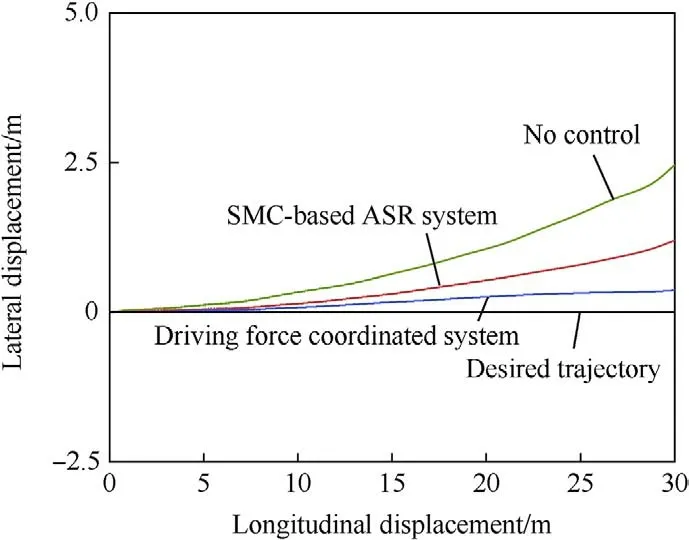
Fig.21. Vehicle driving trajectory on a μ-split road.

Table 4 Statistics of estimation error of road adhesion coefficient for the docking road simulation.

The estimated values of the two methods were similar to the actual values in trend,but when the road condition changed suddenly,the estimated values of the fuzzy method and the actual value diverged significantly.It can be seen from Table 4 and Fig.22 that the estimation accuracy of the fuzzy method was not ideal.However,the accuracy of the proposed RLS method was better than that of the comparison fuzzy method;even when,at the fourth second,the road condition changed suddenly,the RLS method tracked the actual value with high accuracy,which verifies that the proposed method has good estimation accuracy for a docking road with a variable coefficient of adhesion.

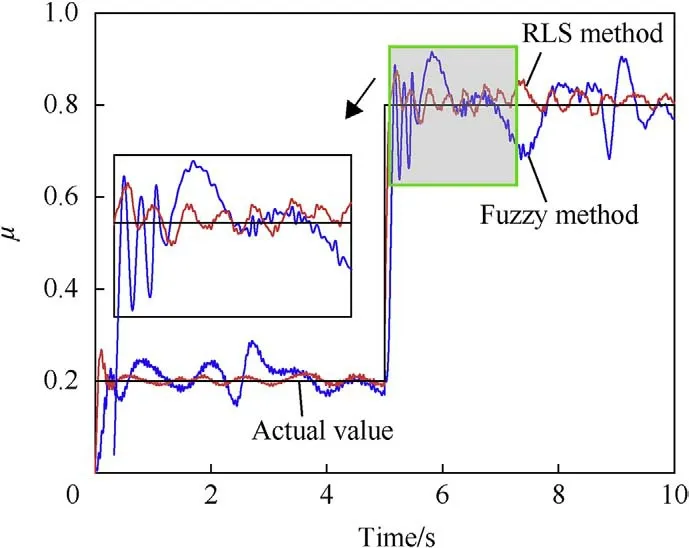
Fig.22. Estimation of road adhesion coefficient for the docking road simulation.

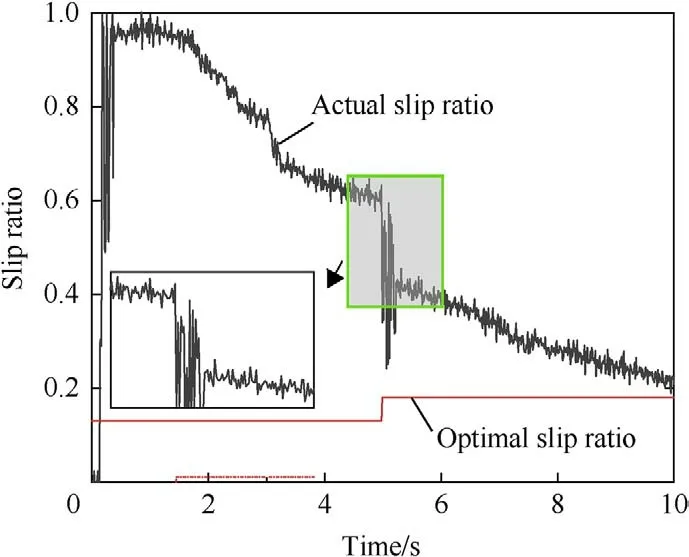
Fig.23. Wheel slip ratio of the vehicle starting and accelerating on a docking road without driving force control.

When there was no driving force control applied on the vehicle,the driving wheel slip was quite noticeable,and the deviation between the actual tire slip ratio and its optimal value was large,with a maximum value of 76%.This condition had a serious impact on the vehicle dynamics and stability(Fig.23).The SMC-based ASR system played a certain role in reducing excessive driving wheel slip.It reduced the difference between the actual and the optimal slip ratio during the entire driving process,but the change in road condition could not be identified,and the fixed optimal slip ratio could be used only for control.In addition,the chattering phenomenon of the system was clear because of the characteristics of sliding mode control (Fig.24).The proposed driving force coordination control system quickly detected the sudden change of road adhesion coefficient,and rapidly adjusted the optimal slip ratio according to the situation.The driving force coordination control system detected the abrupt change of road information in the fourth second.It is obvious that when the vehicle was driving on the slippery road with μ=0.2 for the first 4 s,the SMC-based controller quickly reduced the actual slip ratio to near its optimum with a low adhesion road surface.However,when the vehicle drove on the road with μ=0.8,the control system determined the optimal slip ratio of the road with a high adhesion coefficient.This enabled the actual slip ratio to converge to the new optimal value rapidly,and ensured that the average error of the slip ratio in the system stability control did not exceed 10% (Fig.25).

Fig.24. Wheel slip ratio of the vehicle starting and accelerating on a docking road with the SMC-based ASR system.

Fig.25. Wheel slip ratio of the vehicle starting and accelerating on a docking road with driving force coordinated control.

6.Conclusions

EVs with eight in-wheel motors exhibit strong nonlinearity and unknown uncertainties.Furthermore,the driving road and working conditions are more complex and specific compared with those related to conventional four-wheel civilian vehicles;therefore,it is difficult to ensure dynamic control of such EVs.Considering this issue,this paper proposes a new driving force coordination system for EVs with eight in-wheel motors.

The UKF algorithm is used to estimate the tire forces and the RLS method is employed to compute the road adhesion coefficient.With this system,the optimal wheel slip ratio of the current road conditions is obtained in real time,which enables overcoming the poor adaptability of many traditional ASR systems caused by their reliance on a fixed optimal slip ratio for control.In addition,the controller based on SMC&CI was designed as the core of ASR to obtain the adjusting torque.Furthermore,by setting the ASR intervention conditions,the regulating torque output by ASR was integrated with the feedforward control torque instructed by the driver to achieve a flexible and integrated driving force control performance.The results of the HILS experiment confirmed the superiority of the proposed control system in providing a higher level of driving performance and steering stability for the 8×8 inwheel motor drive vehicle.

For the future development of EVs,this control system can provide guidance for applications of vehicle driving,especially for improving the adaptability of multi-wheel special vehicles to different driving environments,and for allowing them to perform under emergency motor scenarios.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the Weapons and Equipment Pre-Research Project of China (No.301051102).