一种求解等效并行机调度问题的改进遗传算法
2022-02-14吴杰程钱晨红潘厉冰
刘 宇,吴杰程,钱晨红,潘厉冰
(温州大学 机电工程学院,浙江 温州325035)
并行机生产是目前工业上普遍采用的一种生产方式,如LED半导体晶粒拣选工艺[1]等。并行机调度是车间生产调度中的一个重要问题。关于并行机调度问题的研究,通常需假设所有并行机在调度过程中持续可用,但实际调度生产过程经常会出现由机器故障或长时间运行损耗等导致的停机问题,因此必须进行预防性维修来保障正常生产过程[2]。此外,在精益生产和无库存生产方式下,工件通常不都是同一时刻到达而是在计划范围内随机到达的。因此,安排生产计划时应考虑工件到达时间的约束。
对于预防性维修的并行机调度问题,已有不少学者进行了研究,如:刘民等提出一种解决较大规模并行机调度问题的遗传算法[3];常俊林等针对并行多机调度问题,基于遗传算法的搜索能力提出一种能改善求解质量的混合启发式算法[4];金寿松等采用两段染色体编码方式,对种群的初始化过程进行优化,并结合自适应算子改进了遗传算法[5];江才林等针对考虑周期预防性维护的异速并行机系统,提出了一种混合遗传算法[6];蒋凯丽等针对具有时间窗的预防性维护并行机下的混合流水线系统,提出了一种构造式算法[7]。分析有关文献可知,对于同时考虑预防性维修和工件到达时间的等效并行机调度问题,用传统遗传算法求解可以获得不错的结果,但存在种群中个体多样性不强、易陷入局部最优等问题。为此,本文提出一种基于自适应交叉变异概率以及灾变机制的改进遗传算法。
1 并行机调度问题
并行机调度问题可描述为:将n个工件安排在m台并行机中的一台机器上加工,实现预期目标的最优。
1.1 并行机调度的五要素
(1) 待加工工件集。设J={J1,J2,…,Jn}是一组数量为n的不可中断加工工件。Jj表示第j(j=1,2,…,n)个工件。其中工件Jj的加工时间为p[j],工件Jj的到达时间为r[j],且每个工件到达的时间是动态的。
(2) 加工机器集。设M={M1,M2,…,Mm}是m台机器的集合。
(3) 预防性维修(Preventive Maintenance,PM)。机器需要进行弹性的PM,以保证机器能正常生产。本文考虑的预防性维修均为弹性维修形式,即连续加工工件时间或者机器的使用时限不能超过维修时间的门槛(即维护门槛)Tu,且机器上工件Jj的加工时间不超过维护门槛,即p[j]≤Tu。维护作业所需时间(即维修时间)固定为t。
(4) 约束条件。①加工过程中不允许抢占工件,也不允许中断工件供应;②每台机器在同一时刻只能加工一个工件,且每个工件在同一时刻只能在一台机器上加工;③工件之间没有加工优先级之别;④每个工件都有自己的到达时间;⑤工件Jj的到达时间r[j]和加工时间p[j]都是预先给定的;⑥机器的维修门槛Tu和维修时间t都是预先给定的;⑦同一工件在任一台机器上的加工时间相同。
(5) 调度目标。调度目标是最大完工时间的最小化。
1.2 并行机调度问题的甘特图
根据调度问题的三域表示法[8],可将考虑PM与工件到达时间约束,以最小化完工时间为目标的调度问题标记为Pm/r[j],FPM/Cmax。图1所示为考虑PM和工件到达时间约束的多台等效并行机单目标调度问题甘特图。

图1 考虑PM和工件到达时间约束的多台等效并行机单目标调度问题甘特图
考虑PM和工件到达时间约束的多台等效并行机单目标调度问题包括M1,M2,…,Mm机器上所有工件的排序。Ji[k]表示机器Mi上第k个位置加工的工件。r[i][k]表示工件Ji[k]的到达时间,p[i][k]表示工件Ji[k]的加工时间,Ti[a]表示工件Ji[k]的总加工时间。PMia表示对机器Mi的第a次PM。C[i][nm]表示机器Mi的完工时间。
2 数学规划模型
2.1 参数定义
C[j]:工件Jj的完工时间,j=1,2,…,n。
Ts,[i][k]:机器Mi上第k个位置的开始加工时间(i=1,2,…,m;k=1,2,…,n-m+1)。
Q[i][k]:机器Mi上第k个位置的累计加工时间。
Tc,[j][k]:工件Jj在机器Mi上第k个位置的完工时间。
Cmax:m台机器中最大的完工时间。

2.2 决策变量设置
X[i][j][k]:若工件Jj在第i台机器Mi的第k个位置上加工,则为1;否则为0(i=1,2,…,m;j=1,2,…,n;k=1,2,…,n-m+1)。
Y[i][k]:若在机器Mi的第k个位置加工工件后需要维护机器,则为1;否则为0。
2.3 模型构建
以最大完工时间最小为目标的数学模型为:
Min.Cmax
(1)
每台机器的每个位置最多加工一个工件,每个工件也必须在一台机器的一个位置上加工。由此可列出下列式子:
(2)
每台机器的最后一个位置不需要维修。由此可列出下列式子:
Y[i][n-m+1]=0
(3)
机器Mi第k个位置的开始加工时间与累计到达时间的关系为:
(4)
机器Mi第k个位置的开始加工时间要大于等于上一个工件的完工时间与该位置的PM时间之和。由此可列出下列式子:
Ts,[i][k]≥Tc,[j][k-1]+Y[i][k-1]·t
(5)
机器Mi第k个位置的完工时间等于该位置的开始加工时间与该位置上工件的加工时间之和。由此可列出下列式子:
(6)
每台机器上各位置的累计加工时间为:
(7)
机器Mi的累计加工时间的约束可表示为:
为尽早安排工件的加工,决策变量应满足下列条件:
(9)
工件Jj完工时间的约束可表示为:
(10)
最大完工时间可表示为:
Cmax≥C[j]
(11)
3 改进遗传算法
为解决考虑预防性维修的并行多机调度问题,这里给出了图2所示基于灾变机制的改进遗传算法流程。相比传统遗传算法,本文提出的算法采用随机与启发式混合方法生成初始种群,设计了自适应交叉概率、变异概率和灾变算子。

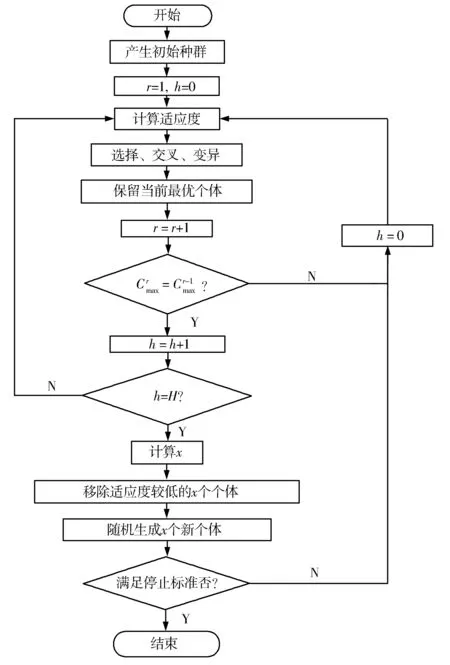
图2 基于灾变机制的改进遗传算法流程
3.1 设计编码并生成初始种群
编码方式采用自然数编码,1~n表示工件号,用0区别两台机器,两个0之间的数表示在一台机器上加工的工件序号。
Pm/r[j],FPM/Cmax问题具有下列性质:若每台机器的完工时间趋于一致,则最大完工时间趋于最小;在机器都空闲的情况下,到达时间早的工件先加工;在已经确定每台机器加工工件顺序的情况下,最优解一定是耗费时间最少的[8]。根据文献[9],若能尽量使机器满载,则最大完工时间趋于最优。
为确保初始种群的质量和多样性,本文利用启发式算法生成80%的初始种群,让剩余的20%种群随机生成。
按启发式算法生成较优初始种群的具体步骤有6个。
(1) 根据工件Jj到达时间r[j]从小到大的顺序,对每个工件的序号进行逆排序。如果两个工件的加工时间相同,则将工件序号小的排在前面;如果两个工件的到达时间相同,则将加工时间短的工件排在前面。
(2) 取前m个工件,分别安排在m台机器的第一个位置。
(4) 将剩余的n-m个工件随机排序并安排加工,若某台机器的完工时间超过了S3,就将相应的工件安排到下一台机器上,以此类推到最后一台机器。
(5) 将剩余工件分配结束,并针对每台机器上的工件,根据r[j]的值从小到大重新排序。
(6) 根据维护门槛Tu,对每台机器上的工件进行满载调整。
3.2 计算目标函数适应度并进行个体的选择复制
个体I的适应度为:
(12)
式中,Cmax(I)为对应个体I的目标最大值。
根据适应度大小,采用轮盘赌法[10]选择个体,并将其复制到后代种群中。
3.3 自适应操作
在文献[11]的基础上,本文采用一种能自适应调整交叉概率和变异概率的方法,进一步提高遗传算法的求解速度和收敛速度,以实现遗传操作后的种群多样化。
交叉概率为:
(13)
式中:gmax为后代种群中个体的最大适应度;gmin为后代种群中个体的最小适应度;g′为遗传操作中两个个体中较大的适应度;gavg为后代种群中个体的平均适应度;k1、k2、k3、k4均为指定系数,且1>k1>k2>k3>k4>0。
变异概率为:
(14)
式中,1>k5>k6>k7>k8>0。
只要指定kq(q=1,2,3,4,5,6,7,8)的值,就可以实现交叉概率和变异概率的自适应调整。
3.4 交叉操作
将随机选择的两条染色体分别作为父代1和父代2,并随机采用两种交叉方法(交叉方法A和交叉方法B)中的一种,进行交叉操作,生成两个子代。
(1) 交叉方法A:在两个父代P1、P2中各选择一个基因段,进行交换。基因段的特点在于其两个端点各为两个相邻的0。对于较优的父代,选择最大完工时间值最大的一段基因;对于较差的父代,选择最大完工时间值最小的一段基因。交叉方法A的操作如图3所示。

图3 交叉方法A的操作示意图
(2) 交叉方法B:鉴于工件数量为n、机器数量为m,可从1到n+m+1随机生成两个交叉点,将两个父代P1,P2各分成3个区域;从集合{1,2,3}中随机生成一个整数γ。如果γ=1,则交换P1,P2的前段区域;如果γ=2,则交换P1,P2的中段区域;如果γ=3,则交换P1,P2的后段区域。这里给出了γ=2 时交叉方法B的操作示意图(图4)。
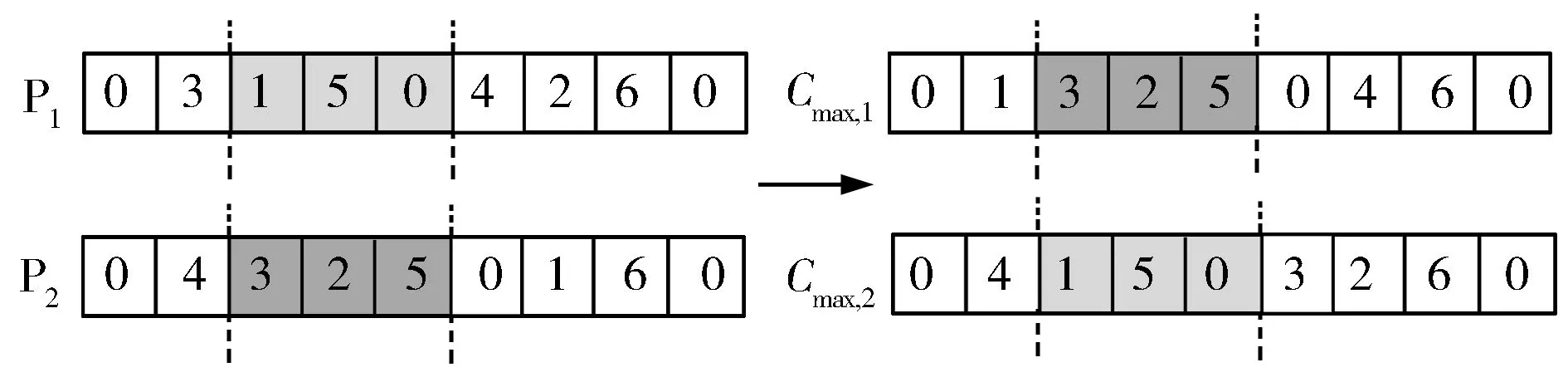
图4 γ=2时交叉方法B的操作示意图
3.5 变异操作
对随机选择的染色体进行变异操作时,应先后采用两种变异方法(变异方法A和变异方法B),进行变异操作。
(1) 变异方法A:在前50%代的种群中,随机选择两个基因,进行交换(若取到了0,则需要重新选择)。变异方法A的操作如图5所示。

图5 变异方法A的操作示意图
(2) 变异方法B:在后50%代的种群中,随机选择一个基因段,并对基因段内的排序进行倒置处理。变异方法B的操作如图6所示。

图6 变异方法B的操作示意图
3.6 灾变操作
为避免遗传种群出现“早熟”,可在传统遗传算法中加入灾变机制,运用灾变算子进行灾变操作[12]。在多次迭代后,大多数个体与最优个体相似度较高时,应进行灾变操作。灾变操作是指,保存当前种群中部分较优秀个体而删除其他个体,并随机产生新的个体,对种群进行补充,从而提高种群的多样性[13]。
在灾变操作时,传统上要将灾变规模设置成常数,若迭代后期使用前期的较大灾变规模,则会导致求解速度变慢以及最优解的质量变差。为保障算法的收敛性和最优解的质量,本文设置了动态的自适应灾变规模(即灾变算子),使其能随着遗传种群迭代次数的改变而发生变化。灾变算子可表示为:
x=е-μr/Rx1
(15)
式中:μ为控制变量,1>μ>0;R为最大迭代次数;x1为初始设置的灾变规模。
设置灾变计数h′,用于记录前一个种群最优个体与后一个种群最优个体相同时迭代的次数。如果h′达到了预设的最大灾变次数H,则需进行灾变操作并启用灾变算子。
灾变操作的具体步骤为:①针对遗传种群内所有个体,根据适应度从小到大进行排序;②计算当前种群迭代次数下的灾变规模(即灾变的个体数)x;③删除当前种群适应度较低的前x个个体,而保留其他较优秀的个体;④按随机规则产生x个新个体,加入当前种群,构成灾变操作后的新种群。
3.7 算法停止
当算法满足迭代次数为200时,停止算法,得到最终结果。
4 实 验
4.1 实验设置
为了评估数学规划模型与改进遗传算法的求解效率、最优解质量,本文进行了相应的实验和计算。实验数据包括机器参数、工件参数和PM参数等。其中:机器参数为机器的数量m;工件参数包括工件数量n、加工时间p[j]、到达时间r[j];PM参数包括维护门槛Tu和维护作业所需时间t;灾变机制参数包括初始设置的灾变规模x1、预设的最大灾变次数H。
实验以中小规模问题为例,工件数量n设置了7种,即n={6,7,9,10,11,12,15};工件加工时间p[j]服从统计分布U[1,10];Tu设置了3个水平,即Tu={10,15,20};t设置2个水平,即t={2,5}。机器数量m设置为3。Tu和t一共产生了6种组合。实验组合总共有42种,每种组合做10次实验,结果取平均值。
初始设置的灾变规模x1为50,预设的最大灾变次数H为5。k1=0.8,k2=0.6,k3=0.5,k4=0.2,k5=0.1,k6=0.05,k7=0.03,k8=0.01。
本文利用Dev-C++语言编写改进遗传算法的程序,并在IBM ILOG CPLEX Optimization Studio Ver. 12.7.1平台上构建了数学规划模型;针对不同工件数量,采用数学规划模型、传统遗传算法、改进遗传算法,分别求得最优解,并统计了运算时间。
4.2 结果分析
采用数学规划模型、传统遗传算法、改进遗传算法求解的结果和平均运算时间分别见表1、表2。表1中偏差程度的计算公式为:
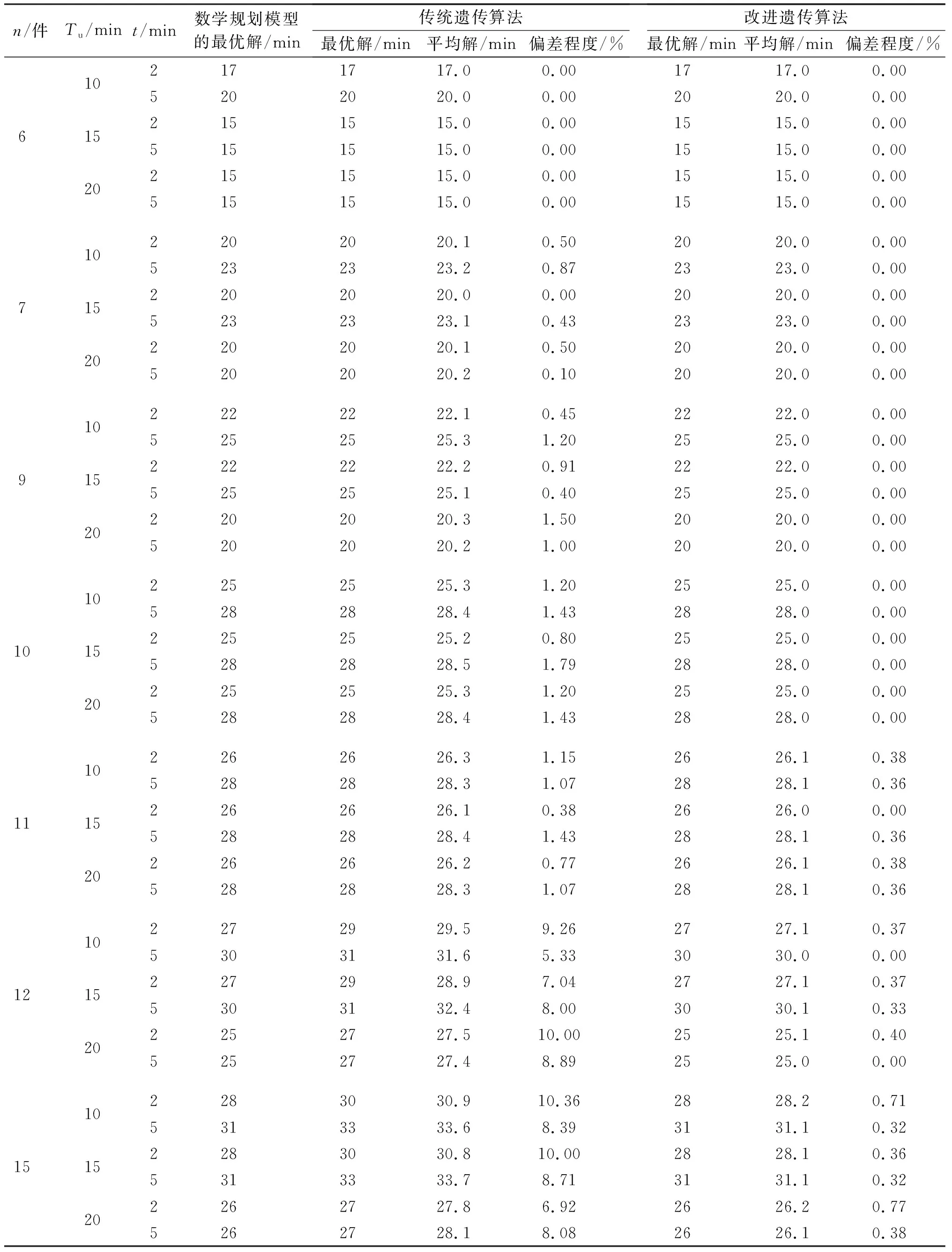
表1 数学规划模型、传统遗传算法和改进遗传算法的求解结果
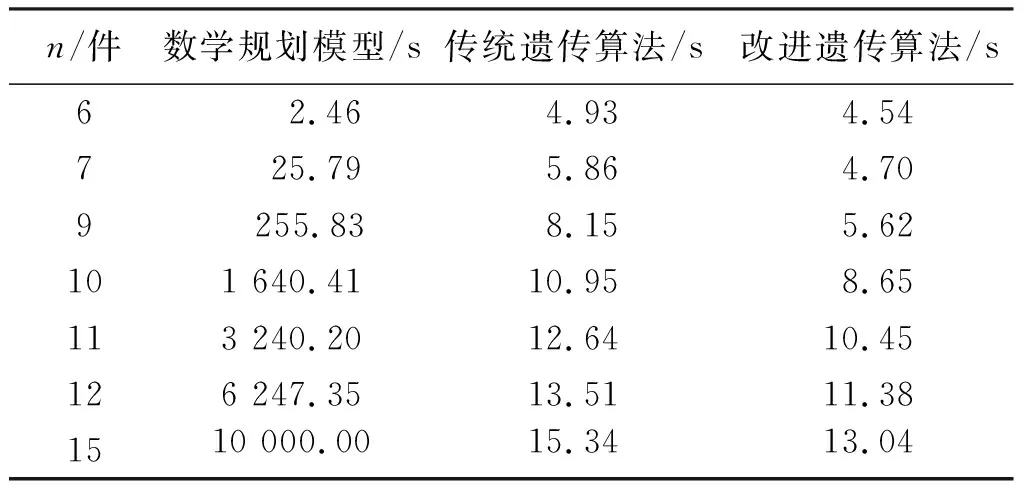
表2 数学规划模型、传统遗传算法和改进遗传算法的平均运算时间

(16)
由表1可知:对于小规模问题的求解来说,数学规划模型具有明显的优势;从偏差程度来看,本文提出的改进遗传算法求解结果比传统遗传算法稳定,且求解质量优于传统遗传算法,具有更好的搜索能力。随着工件数量的增大,改进遗传算法相对传统遗传算法的优势越来越明显:当工件为6件时,改进遗传算法与传统遗传算法的偏差程度都近似于0.00;当工件为15件时,对于Tu和t的6种组合来说,传统遗传算法的平均偏差程度是改进遗传算法平均偏差程度的21.01倍。
由表2可知,对于小规模问题的求解来说,数学规划模型虽可得到最优解,但随着工件数量的增大,其运算时间明显增加。这是因为调度问题的可行解空间随着工件数量的增大呈指数型增加,而数学规划模型的求解需要搜索全部可行解空间,所以运算时间会急剧增加。而遗传算法仅搜索其中一部分解即可,因此效率更高。对于中小规模问题的求解来说,改进遗传算法的灾变算子虽然会导致其运算时间的增加,但改进遗传算法有更强的限制搜索空间的能力,因此总体上,改进遗传算法比传统遗传算法的运算效率更高,且随着工件数量的增大,两种算法的平均运算时间差异越来越大,从工件为6件的0.39 s增加到了工件为15件的2.30 s。
4.3 改进遗传算法再验证
为进一步验证加入灾变机制的改进遗传算法的性能,选取n=15,m=3,t=2,Tu=10的实例,以最大完工时间为目标函数,最大迭代次数为200进行了实验。遗传算法加入灾变机制前、后的收敛曲线如图7所示。
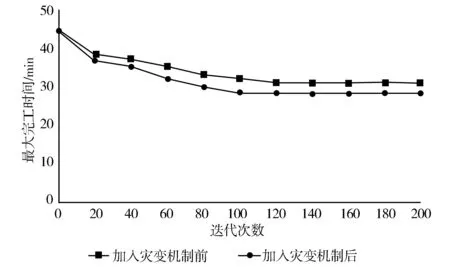
图7 遗传算法加入灾变机制前、后的收敛曲线
从图7可看出:在相同迭代次数下,加入灾变机制后遗传算法的解质量优于加入前;在目标值相近的情况下,遗传算法加入灾变机制后的迭代次数小于加入前的迭代次数,由此可认为,迭代过程中加入灾变机制提高了算法的搜索能力;在目标值相近的情况下,加入灾变机制前遗传算法在115代收敛于目标值30 min,而加入灾变机制后遗传算法则在120代收敛于目标值28 min。
5 结 语
本文针对预防性维修的等效并行机调度问题,考虑工件的到达时间和维修策略约束,以最大完工时间的最小化为目标,建立了相应的数学规划模型,并提出了基于灾变机制的改进遗传算法。通过改变初始种群的生成方式,利用自适应灾变算子并引入灾变机制,大大提高了算法的搜索能力和求解质量。实验证明,改进遗传算法用于求解等效并行机调度问题是有效的。然而,本文只研究了单目标的并行机调度问题,并行机的实际调度问题还存在工件投放时间、交货期、交货时间等诸多约束和目标。因此,未来可根据解决实际调度问题的需要进行多目标动态调度方法的研究。
