基于ALO-BP神经网络和机械零件加工特征的工艺方案决策

李 群，贾家乐，潘阳洋，陈文笛

(1.沪东重机有限公司 技术中心，上海 200129；2.江苏科技大学 机械工程学院，江苏 镇江212100)

随着制造业的发展，大型制造企业逐步积累了大量工艺知识，积累了较丰富的企业工艺设计成果和经验。但是，目前大部分制造企业只是对这些工艺数据进行结构化的存储，缺少有效的分析及应用手段。如何利用这些宝贵的工艺知识，提高企业的工艺设计效率和制造质量，是大力推进数字化制造背景下企业急需解决的关键问题[1]。基于加工特征的工艺决策技术能根据加工特征、工艺知识，做出最优工艺路线的决策。它是计算机辅助工艺过程设计(Computer Aided Process Planning，CAPP)的关键技术之一，在工艺设计领域得到了较广泛的应用。开展工艺知识的应用技术研究，优化基于加工特征的工艺方案决策方法，提高机械零件加工工艺方案决策的效率和质量，可大幅度提高制造企业的工艺设计水平。迄今为止，国内外学者和相关企业已提出多种解决工艺决策问题的方法，如基于规则的推理和特征库的匹配等方法[2]。但这些方法普遍存在智能化程度较低、决策结果准确率不高等问题。随着算法与人工智能的发展，神经网络技术在各领域的应用越来越广泛。目前，在机械零件的加工工艺决策过程中用神经网络技术确定最佳工艺方案是完全可能的[3]。李春磊等提出一种利用规律和神经网络技术，挖掘、修正特征加工链，对符合加工链需求的信息进行概率分析并修正加工路线，输出最优工艺方案的方法[4]。但这种方法只适用于有规律的工艺信息，对于一些复杂的零件信息，决策效果较差。郭继通等提出了利用遗传算法改进神经网络的方法，对软脆工件的研磨加工进行工艺方案决策[5]。该方法通过优化的反向传播神经网络(Back Propagation，BP)智能预测研磨过程，确定主要的工艺参数，提高了决策过程的智能化程度，但用遗传算法进行优化的过程容易出现局部最优问题，导致了其决策准确率不高，难以应用于实际的加工生产。Jiang等提出一种实例推理方法，在人工赋予特征权值后计算实例之间的相似度，实现了凸轮磨削过程加工工艺的决策[6]。该方法需要利用大量的传统工艺数据和专家经验，虽然能从很大程度上提高决策结果的准确率，但过分依赖于主观经验，决策效率较低，无法适应现代智能制造业的高速发展。

基于前人的探索和经验，本文提出一种基于ALO-BP神经网络和机械零件加工特征的工艺方案决策方法，通过蚁狮优化(Ant Lion Optimizer，ALO)算法，优化BP神经网络对工艺方案决策参数的学习过程，并获取优化后的权值和阈值，从而能结合企业传统工艺知识库中的工艺知识，完善加工工艺的决策流程，实现机械零件加工工艺方案的决策。

1 加工工艺智能决策的总体方案设计

机械零件加工工艺智能决策的总体方案如图1所示。该方案包括数据源模块和智能决策模块。

图1 机械零件加工工艺智能决策的总体方案

数据源模块的实现，需首先根据零件的结构层次模型和加工特征信息模型，获取零件三维模型和加工特征相应信息(如特征名称、特征集合、设计信息编码和工艺方案)；然后，对获取的数据进行处理，基于零件加工特征集合、设计信息编码和工艺数据，构建工艺结构层次模型；最后对各零件的加工特征进行信息整合，形成基于零件加工特征的工艺方案向量组。

智能决策模块的实现，需首先对基于零件加工特征的工艺方案向量组进行分割，形成相应的输入特征矩阵和目标矩阵；然后，对基于机器学习的智能决策模型进行训练；最后，将训练得到的参数用于加工工艺路线，进行工艺方案的智能决策。

2 加工工艺智能决策模型的构建

2.1 工艺数据预处理

通过读取企业的工艺资源库和保存的历史加工特征信息，获取影响加工工艺的一些因素。如孔类零件，其加工工艺的影响因素包含零件直径、零件材料、热处理方式、精度等级要求和表面粗糙度要求等。将这些影响因素和最终的工艺决策方案结合起来，组成基于零件加工特征的工艺方案向量组。

(1) 基于零件加工特征的工艺方案集构建。对影响零件加工特征的各种设计参数及其与加工方案形成的一一对应关系进行编码，作为向量组构建时的比较集。

(2) 工艺方案向量组的编码和构造。根据各加工特征的工艺知识库，将基于各零件加工特征的工艺方案转换为特征编码，构建相应的向量组。

由于不同零件的加工特征之间存在差异，对应于相似加工特征的工艺方案并不是一成不变，而是具有可变性和可组合性的，因此在构建向量组时，可将不同零件的同类型加工特征的设计参数集成到向量组中。由于影响工艺方案的设计参数是不同类型的，需在归一化处理后才可输入神经网络进行训练。这里以孔类零件特征为例，其具体的归一化处理规则为：①直径d(mm)(归一化处理后记作x1)按照工艺方案的不同分为5段，与不同参数一一对应，当d∈{(0，30]，(30，80]，(80，200]，(200，500]，(500，1 000]}时，x1对应取(0.2，0.4，0.6，0.8，1.0)；②精度等级τ(归一化处理后记作x2)，x2=(12-τ)/8；③表面粗糙度Ra(归一化处理后记作x3),x3=(lg 12.5-lgRa)/(lg 12.5-lg 0.05)；④热处理方式(归一化处理后记作x4)，若采用淬火热处理方式，则x4取1.0，反之取0.0；⑤零件材料(归一化处理后记作x5),主要为合金钢、碳钢、铸铁，分别取1.0，0.5，0.0。

整体工艺设计信息的编码形式为：X=[x1，x2，x3，x4，x5]。

对企业的历史工艺信息进行整理、挖掘、分析，可得表1所示孔类零件加工特征常用的工艺方案。

表1 孔类零件加工特征常用的工艺方案

(3) 工艺方案向量组的表示。本文以矩阵A表示工艺方案的向量组，即

(1)

式中：X1，X2…,Xm均为影响工艺方案的加工特征向量，Y1，Y2…,Ym均为工艺方案向量。

2.2 训练集和决策模型构建

BP是神经网络算法中最成熟、最具代表性的，已被广泛应用于解决机械加工领域的各种决策问题[7-8]。因此，本文基于三层BP神经网络来构建加工工艺路线的智能决策模型。

三层BP神经网络由输入层、隐藏层和输出层三部分组成。基于加工特征和工艺方案的BP神经网络结构模型如图2所示。

图2 基于加工特征和工艺方案的BP神经网络结构模型

首先，获取工艺方案的向量组，并在构建基于神经网络的决策模型时，将工艺方案的向量组分为行向量和列向量两部分；然后，将行向量(X1-Xm)作为神经网络输入层的节点，列向量(Y1-Ym)作为神经网络输出层的节点(这里，列向量的元素数量为构成矩阵的设计参数个数)，构建能够充分反映零件各设计参数对工艺路线影响的训练集。

在基于该训练集构建的BP神经网络决策模型中，输入信息Pin和输出信息Pout满足以下关系：

(2)

式中：Phd为隐藏层信息；f1(·)和f2(·)分别为计算隐藏层信息和输出层信息所用的激活函数；w1和b1分别为计算隐藏层信息所用的权值和阈值；w2和b2分别为计算输出层信息所用的权值和阈值。

为评估当前决策参数的性能，可将神经网络决策模型输出信息与理论输出值之间的均方差作为损失函数E。其表达式为：

(3)

式中：P′out为理论输出值；i为参数序号；n为决策参数的量。损失函数的值越大，说明BP神经网络决策模型的输出信息与理论值偏差越大，需继续进行优化训练。

BP神经网络决策模型经过训练能生成最优决策参数。最优决策参数可用于CAPP系统，对新的工艺方案进行决策。

3 ALO算法在BP神经网络中的应用

传统的BP神经网络在解决小样本、高维度问题时容易陷入局部极值，导致收敛速度减小，网络性能变差，智能决策模型的训练周期变长，而影响模型的决策精度和稳定性。此外，当按照传统的随机生成方式不能生成合适的神经网络初始权值和阈值时，传统的BP神经网络很难获得良好的训练效果。为了解决上述问题，提高模型的性能，需要对传统的BP神经网络进行优化。

ALO算法是2015年Mirjalili提出的一种新型启发式蚁群智能优化算法，引入了随机行走方式、自适应策略和精英策略，具有种群多样、调整参数少、易于实现、优化能力强等优点[9]。该算法近年来已成功应用于无人机航路规划、电力系统无功优化调度、杠杆结构优化等领域。因此，本文采用基于ALO算法的综合优化方法来实现BP神经网络决策模型的性能优化。

3.1 基于ALO算法的BP神经网络优化

(1) 基于ALO算法优化BP神经网络的初始权值和阈值。根据实际的BP神经网络模型，对种群进行编码，生成ALO算法的初始种群；将均方差损失函数作为ALO算法的目标函数，并计算其适应度；当ALO算法满足终止条件或达到最大迭代次数时，记录并提取当前的最优个体；通过解码生成最优初始权值和阈值。

(2) 通过自适应学习调整策略，提高BP神经网络的收敛速度，缩短训练时间。这里的自适应学习控制策略可表示为：

(4)

式中：ηt为学习率；t为当前训练次数；β为小数，通常取0.01～0.03；Et为第t次训练后损失函数的值。显然，当误差变小时，学习率提高；当误差增大时，学习率降低。按式(4)操作，可实现学习率的自适应调整。

(3) 用附加动量法来避免BP神经网络中权值和阈值收敛到局部最优问题的出现。附加动量法的公式为：

(5)

式中：Δwt和Δbt分别为第t次训练反馈过程中权值和阈值的改变量；α为动量因子，一般按经验取值0.95。在没有附加动量的情况下，BP神经网络可能会陷入浅层局部极小值。通过附加额外动量，BP神经网络在不断反馈与优化的过程中能够滑过这些极小值,且能基于反向传播，将与前一个权值(或阈值)改变量成正比的值添加到每个权值(或阈值)的改变量上，从而生成新的权值(或阈值)的改变量。

3.2 ALO算法与BP神经网络的结合

基于ALO算法的BP神经网络决策模型可称作ALO-BP神经网络模型(图3)。

图3 ALO-BP神经网络模型

(1) ALO算法的初始种群编码与解码。由图3可看出，ALO算法中蚂蚁和蚁狮种群的个体位置向量直接反映了各层的权值和阈值。本文将w1，b1与w2，b2合并，延伸成一个行向量，作为ALO算法的个体位置向量。个体位置向量的元素数量D应由矩阵[w1，b1，w2，b2]的元素数量确定，即

(6)

式中：Nw1，Nb1，Nw2，Nb2分别为矩阵[w1，b1，w2，b2]中对应元素的数量，并由输入层节点数量Nin、隐藏层节点数量Nhd和输出层节点数量Nout决定，即

(7)

根据D值生成初始种群M，即

M=[α1，α2，…，αD]

(8)

经过迭代优化，得到最优解B后,按照Nw1，Nb1，Nw2，Nb2将B裁切成4个行向量，并将这4个行向量折叠，使其成为初始矩阵[w1，b1，w2，b2]，完成解码。

(2) ALO算法的初始种群生成与自适应寻优。ALO算法的种群初始化公式为：

(9)

式中：Hr，q为个体位置向量各元素的初始位置，r=1，2，…，N(N为蚂蚁和蚁狮的数量)，q=1，2，…，D；rand(·)为随机函数；U和L分别为搜索空间的上限和下限。因为本文的训练集编码均为1或-1，所以，为保证BP神经网络输出结果仍接近1或-1，经过多次试验，将搜索的初始范围设置为：U=0.5，L=-0.5。

在随机游走过程中，蚂蚁会进入蚁狮的“陷阱”，不断缩减游走范围。因此，搜索空间应满足以下自适应调整策略：

(10)

式中：ct，et分别为ALO算法第t次迭代中所有变量的下限和上限；I为搜索空间的缩减因子。如果迭代次数增加，则I呈线性增加，即

(11)

式中：T是最大迭代次数；ω与当前迭代次数t有关，即

(12)

基于以上策略，搜索范围会逐渐缩小。在最终求出最优个体后，可将其输入BP神经网络进行训练。

BP神经网络训练的输出结果是针对输入各加工特征的最优工艺方案的概率值。针对输出结果，可按下列式子进行二值化处理：

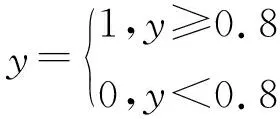
(13)

式中，y为工艺方案输出概率。若概率大于等于0.8则说明工艺方案可行。

4 柴油机典型关键件工艺设计的实例验证

为了验证本文方法的可行性，可首先利用Python语言搭建BP神经网络模型；其次，对零件三维数字化实体模型中的孔类加工特征进行提取，并进行归一化处理；然后，通过加工特征工艺库匹配加工方案，构建神经网络训练集；最后，在Python 3.6环境下运行程序，并采用NX10平台完成辅助验证。

本文根据零件的具体加工方案，将智能决策模型参数设置为：Nin=113，Nout=8；Nhd=12(经过多次实验，该隐藏层节点数量为12时网络性能最优)；学习率ηt=0.035，β=0.02。决策模型训练的终止条件为均方差小于6.5×10-6。输入层到隐藏层的激活函数为Sigmoid函数，隐藏层到输出层的激活函数为Identity函数。此外，ALO算法中蚂蚁与蚁狮种群数量均为10，最大迭代次数为80。

按照上述参数对模型进行了训练和测试。ALO-BP神经网络智能决策模型的损失函数曲线如图4所示。

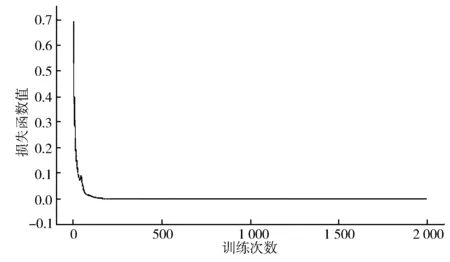
图4 ALO-BP神经网络智能决策模型的损失函数曲线

为了验证所构建决策模型，本文以船用柴油机关键件机架上的典型孔类加工特征为例，采用经过训练的ALO-BP神经网络模型进行了工艺方案决策。机架上4个典型孔类加工特征的工艺信息如表2所示。

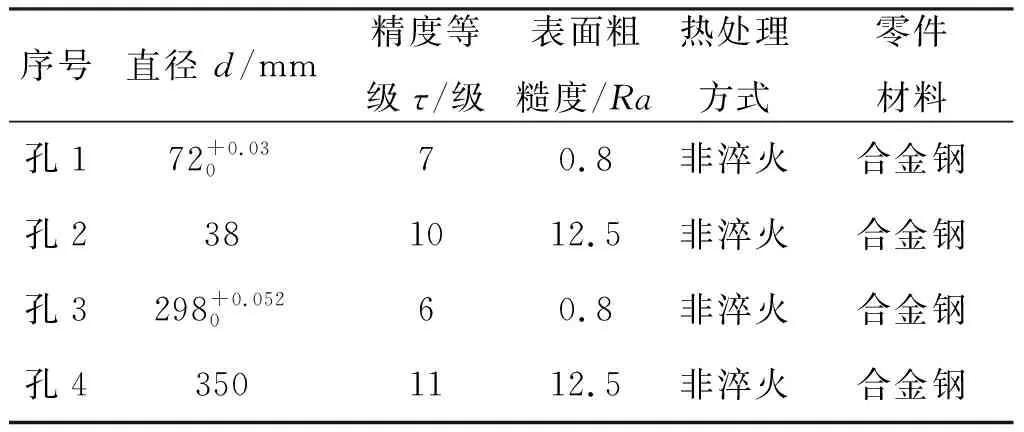
表2 机架上4个典型孔类加工特征的工艺信息

按本文2.1中所述方法,对加工特征的工艺信息数据进行归一化处理，可得表3所示的特征编码结果。

表3 特征编码结果

将表3中编码结果输入训练好的ALO-BP神经网络模型中,进行加工方案的智能决策，最终输出了对应孔1、孔2、孔3、孔4的结果：9，3，9，6。参照表1的工艺方案进行解码可知，机架上4个典型孔类加工特征的工艺方案分别为：“粗镗—半精镗—精镗”、“钻-铰”、“粗镗—半精镗—精镗”、“粗镗”。这一结果符合机架实际的加工要求。

5 结 语

为了提高工艺设计的智能化程度，本文对基于机械零件加工特征的工艺方案决策问题进行研究，提出了一种基于ALO-BP神经网络的决策方法。通过分析加工特征的影响因素进行特征编码和解码；针对传统BP神经网络的缺陷，采用ALO算法进行改进，优化其权值和阈值，提高决策模型的收敛速度和稳定性；以某型号船用柴油机机架上的典型孔类加工特征为例，验证了所构建决策模型在工艺方案决策中应用的有效性和优越性。