电子束偏转扫描线圈的设计与仿真
2022-02-14魏红燕李少林张晨阳张康龙李伯林
魏红燕,李少林,张晨阳,张康龙,李伯林
(桂林电子科技大学 机电工程学院,广西 桂林 541004)
电子束加工是利用高能量密度的电子束对材料进行加工处理的方法。电子束作为一种热源,通过调整其能量密度、束斑直径、束流作用时间等参数,可以产生多种加工方法,如可用于材料焊接和材料表面的强化,同时也可以用于电子束选区熔化、电子束曝光技术[1-5]。电子束增材制造技术(即电子束3D打印技术)通常被用来制作结构复杂且精度高的工件,是一种“自上而下”的电子束加工制造方法,具有可节省加工时间,提高能源材料的使用效率,可量身定做和保护环境等优点[6-13]。其中金属增材制造在生物医药、模具及国防等各个领域中有着良好的发展应用前景[14-17]。
在电子束增材制造技术中,通常采用电子束扫描的方法进行加工,电子束扫描的位置精度误差和电子束束斑的尺寸误差等因素对电子束的加工精度影响极大。因此,开展对电子束偏转扫描磁场的研究,分析偏转扫描磁场误差产生的机理,提出相应的对策和解决方法,具有较强的现实意义。
1 光栅畸变分析
图1(a)给出了均匀磁场示意图,磁场分布是完全均匀的,但是电子束扫描光栅靶面依然存在弱的枕形畸变,可通过改变偏转扫描线圈绕组线匝密度,进而改变偏转磁场的空间分布予以解决。

图1 磁场分布对光栅形状的影响
图(b)为枕形磁场示意图,在y轴两边分布的磁力线是比较稀疏的,产生了桶形畸变[18-21]。
2 偏转扫描线圈设计
2.1 边张角为28°的偏转扫描线圈
当偏转扫描线圈按照余弦分布时,存在区域非整数线圈匝数,为实现工程的可操作性,通常会采用一系列措施调整线圈匝数至整数,这类改动往往会影响实际应用中的磁场分布,导致按照余弦分布产生的磁场存在不均匀等问题。因此,在余弦绕制方法的基础上,设计了近似余弦分布的分布式等效余弦结构绕组。
在分析偏转扫描线圈时,可将其与磁芯设计的单匝线圈相等效,在这种情况下,安匝数为NI,l表示偏转线圈的长度,R表示单匝线圈的半径,θ为偏转扫描线圈的边张角,B0与B2为磁场幂级数的系数,它们都是z的函数。当R≪l时,可得

通过生成弱枕形分布的偏转场,可补偿均匀场产生的枕形畸变,此时B2/B0应略大于零,因此,此时θ应尽量接近且小于30°。选择θ为28°对偏转扫描线圈绕制进行分析,线圈设计模型如图2所示,该模型利用COMSOL软件绘制,线圈绕制参数如表1所示。

图2 分布式等效余弦结构绕组

表1 θ为28°时偏转扫描线圈具体绕制参数
图3为边张角为28°的分布式等效余弦结构绕组x方向的磁通密度、磁力线分布及x、y轴方向磁场分布曲线。
边张角为28°的分布式等效余弦结构绕组的y方向磁通密度、磁力线分布以及磁场分布曲线如图4所示。其x、y方向磁场合成后的磁通密度、磁力线分布及磁场分布曲线如图5所示。

图4 y 方向的分布式等效余弦结构绕组
从图3~5可看出,改进后的偏转扫描线圈磁场分布的均匀度有了较大改善,且所提绕制方法空间中心的磁场均匀度较高,该磁场呈均匀场分布,因此其会产生弱的枕形畸变。

图3 x 方向的分布式等效余弦结构绕组
2.2 边张角为45°的偏转扫描线圈
如图5(a)所示,在线圈进行绕制时会出现绕组重叠现象,这也会影响实际线圈的偏转磁场分布,因此需要对分布式等效余弦结构绕组进行进一步优化,即选择边张角为45°进行偏转扫描线圈设计。由于实际利用的是合磁场所产生的磁场变化,可以省略x、y方向单独的磁场分布分析。边张角为45°时,合磁场的磁通密度、磁力线分布及磁场分布曲线如图6所示。图7为余弦分布式线圈合磁场的合磁场的磁通密度、磁力线分布及磁场分布曲线。

图5 28°边张角x、y 方向磁场合成图
对比图6和图7可得,改进后的45°边张角的偏转扫描线圈的均匀性比单纯余弦分布式线圈更优,且经过线圈绕组匝数的选择,可使偏转磁场呈现弱枕形磁场。在偏转扫描线圈绕制时,无绕组重叠部分,其偏转磁场的误差更低,更易达到预期目标,因此选择边张角为45°的线圈设计方案。
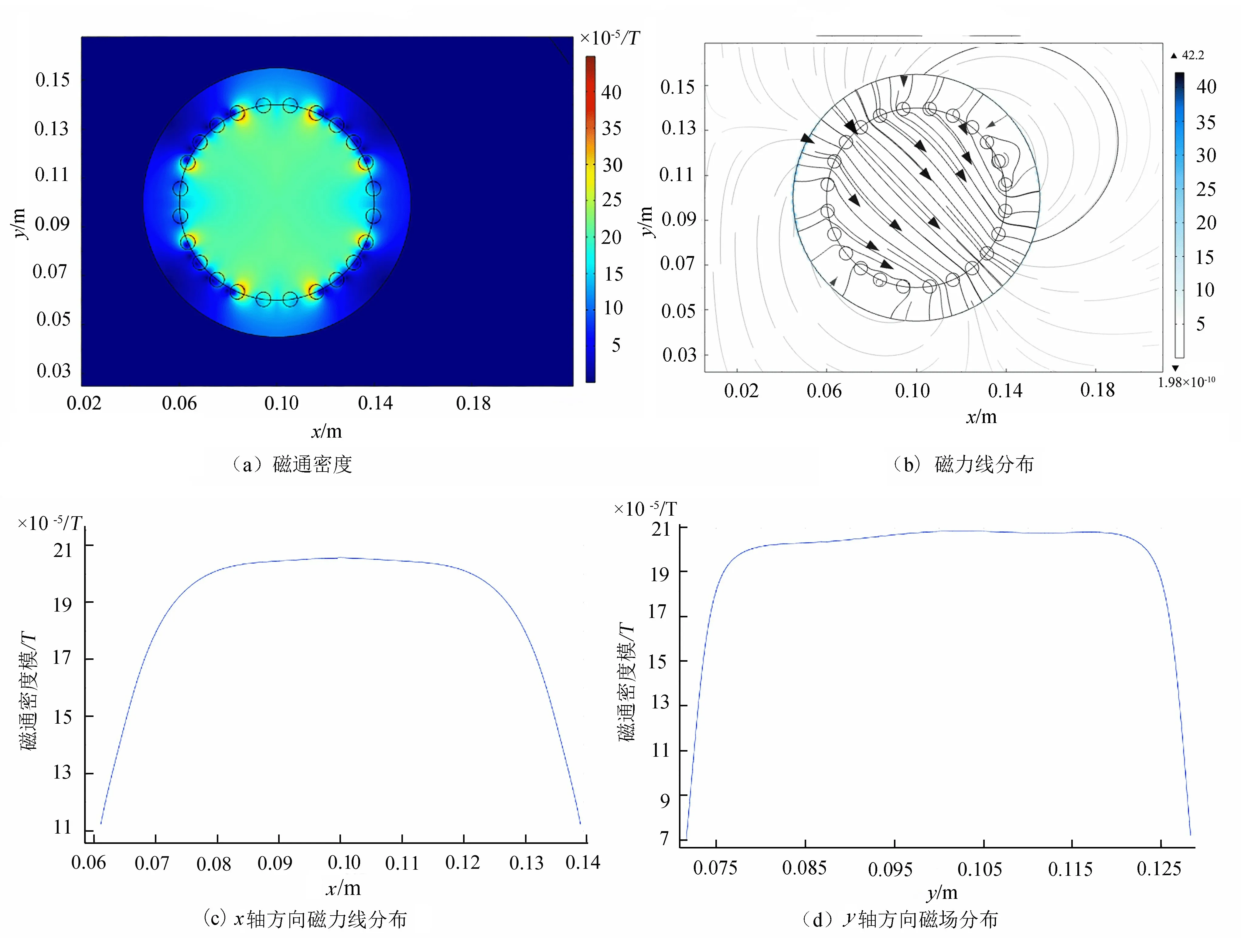
图6 45°边张角x、y 方向磁场合成图

图7 余弦分布式线圈x、y 方向磁场合成
2.3 偏转扫描线圈半径的设计
在线圈实际应用中,根据所需场景变化选择不同半径的偏转扫描线圈,且不同半径所产生的磁场强度有可能会不一样。因此,若只分析一种半径的偏转扫描线圈的磁场分布,并不能完全证明分布式等效余弦绕制方法带来的偏转性能好坏。综上所述,只有比较不同线圈半径的偏转磁场,才能更准确地判断改进后的偏转扫描线圈的优劣。图8为改进前、后线圈半径分别为3、4、5 cm 时,x、y方向的合成磁场在y轴方向的分布曲线。
在匝数一定的情况下,线圈半径的大小会影响磁场强度的大小。因此,设计偏转扫描线圈的半径不能太大或太小,为了使偏转扫描线圈的偏转性能更优以及使偏转中心处的磁场分布更加均匀,线圈的半径应适中。因此,利用在偏转磁场的采样路径中得到的具体磁场数值来对磁场分布均匀度进行分析,定义一个变量K,作为偏转磁场的绝对偏差系数,可综合反映线圈的偏转性能[22]。
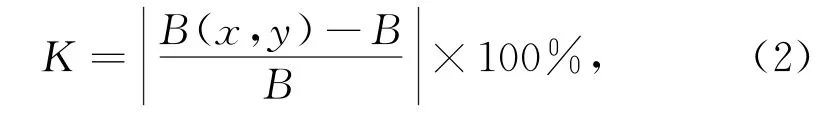
式中:B表示磁场中心的磁感应强度;B(x,y)表示在选择的采样路径范围内任意一点处的磁场强度。用K值对偏转性能的优劣进行评价。根据式(2)及图8计算出不同情况下的K值,数据如表2所示。
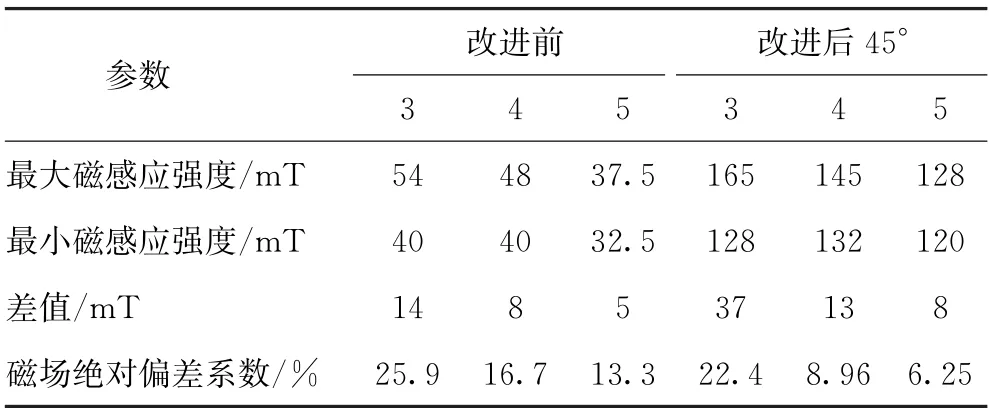
表2 不同情况的偏转扫描线圈K 值 cm
由图8及表2可得,在同样匝数情况下,K值改进前比改进后大,因此改进后的分布式等效余弦结构绕组具有更好的均匀度,也就有更好的偏转性能。4 cm 线圈的磁场在边张角为28°时的磁场绝对偏差系数最小,此时具有较高的磁场均匀度,因此选用4 cm作为线圈的半径。
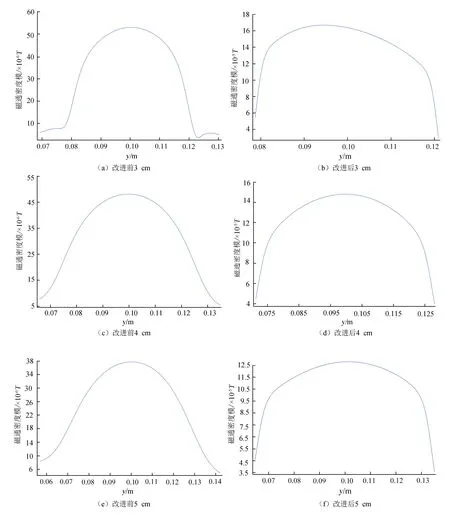
图8 改进前、改进后的磁场分布曲线
3 结束语
1)在余弦绕制法则的基础上,设计了分布式等效余弦结构绕组,计算出了该偏转扫描线圈的边张角,并给出了偏转扫描线圈的具体绕制方法。
2)采用COMSOL软件建立了分布式等效余弦结构绕组的几何模型和有限元分析模型,分析了边张角为28°的x、y方向以及合磁场各自的x、y轴方向的磁通密度、磁力线分布及磁场分布曲线,证明了分布式等效余弦结构绕组的磁场分布均匀且呈弱枕形场,其可改善均匀磁场的弱枕形畸变。
3)分析了边张角为45°合磁场的磁通密度、磁力线分布以及磁场分布曲线,其同样呈现弱枕形场,且制作简单,较28°边张角更优。
4)对比偏转扫描线圈不同线径改进前、后合磁场的磁场分布曲线,证明了分布式等效余弦结构绕组的有效性,并最终确定偏转扫描线圈的半径为4 cm。
