采空区冒落带内破碎岩体的渗流特征与渗透性试验研究

徐树媛，张永波，时 红，相兴华

(1.山西能源学院地质与测绘工程系，山西 晋中 030600；2.太原理工大学水利科学与工程学院，山西 太原 030024；3.太原理工大学环境科学与工程学院，山西 太原 030024)

工程实践中，大多数流体在多孔介质和裂隙介质中流动时渗流速度小，流体运动服从达西定律；但在大孔隙、颗粒粗糙的强非均质介质中，流体渗透流速较大，惯性力占主导地位，渗流系统的线性关系发生偏移[1-4]。有研究表明，在矿山岩体破碎带中，地下水的流动既不满足线性渗流，也非自由的紊流，而是属于高速非达西渗流系统[5]。采空区冒落带内破碎岩体属于堆积破碎岩石[6]，即岩体破碎、垮落后岩块堆积并再次压实。一方面，采空区含水破碎带内的岩体渗透性剧增，易发生突水和淹井事故；另一方面，采空区含水破碎带内煤岩体强度降低，地下水渗流作用易诱发岩体失稳破坏，导致瓦斯突出。目前，数值模拟计算是矿井涌水量预测与含水层受开采影响程度评价的重要手段，计算过程中地下水流运动状态与水文地质参数的确定是模拟结果是否可靠的重要保障。因此，研究采空区冒落带内破碎岩体中地下水的渗流行为是一个基础研究课题，与矿井突水灾害、瓦斯突出灾害防治和高效抽采、围岩稳定性控制以及地下水资源保护等一系列重大课题有关，对促进煤矿生产安全与保护生态环境具有重要的理论和工程实际意义。

目前，已有学者对采空区内破碎岩体中地下水的渗流行为进行了研究。如吴金随[6]、陈占清等[7]、刘玉[8]基于矿井水害防治，对裂隙岩体的非线性渗流行为进行了研究，并分析了系统的稳定性；Salahi等[9]利用填充柱渗流试验观测了两种多孔介质内的非达西流，并得出最佳的经验公式；Shi等[10]开展了不同孔隙度颗粒灰岩非达西流动特征的试验研究；张建营[11]通过3种类别破碎岩石的渗流试验，系统地研究了破碎岩体的非线性动力学行为。岩石的渗透性除与围岩压力相关外[12]，还与其空隙特征有明显的关系。如van Lopik等[13]和Li等[14-15]探讨了孔隙结构与粒径分布对多孔介质渗流流态的影响；张东等[16]建立了不均匀多孔介质渗透率的空间分布与其等效渗透率的关系表达式，开展了采动后破碎岩体渗透性能的研究；王玉涛[17]利用三维空间动态分布模型，获得了采空区多孔介质空隙率与渗透率的空间和时间分布。

上述这些研究成果多集中于整个破碎带渗透性能的研究以及时间尺度下的渗流模型，而基于采空区冒落带内非均质多孔介质渗流特征的研究相对较少，且缺乏采空区冒落带内破碎岩体渗透系数与空隙率的量化关系及其空间分布特征的研究。由于颗粒的非均质性对于渗流流态转变有着重要影响，因此本研究针对采空区冒落带内破碎岩体的非均质性以及裂(空)隙的分布特征，通过渗透性试验测试不同空隙率冒落带内破碎岩体的渗透系数，建立了采空区冒落带内破碎岩体渗透系数与空隙率的相关关系，分析了采空区冒落带内破碎岩体渗透性能的空间变化规律。

1 采空区冒落带内破碎岩体的渗透性试验

1.1 试验材料与装置

受采动影响，位于采空区上方的顶板岩层断裂、破碎并垮落，以岩块形式杂乱堆积于采空区冒落带内，在上覆岩层的荷载作用下，破碎岩石产生滑动或滚动，岩体棱角进一步破碎，块石颗粒充填孔隙，使破碎岩体更加密实。由于采空区冒落带内块石颗粒的粒径大小不一，且形状极不规则，故在实验室条件下，对所取常村煤矿S6采区3号煤层顶板岩样进行破碎，而后根据岩块粒径的分级情况，参照模拟试样的直径要求以及岩石试验对缸筒内径与模拟试样直径的比值限制[18]，本次试验的模拟试样选用最大粒径为30 mm的碎石作为试验材料。为了研究岩石破碎程度与裂(空)隙率对采空区冒落带内破碎岩体渗透性能的影响，获得较好的裂(空)隙率梯度，需要将碎石按照不同粒径进行组合与测试。考虑到破碎岩石的粒径构成中既有较大的石块，又有较小的砂砾，因此本研究选择3种粒径的碎石(Ⅰ为5～10 mm、Ⅱ为10～20 mm、Ⅲ为20～30 mm)为主要材料，并辅以粗砂(Ⅳ为0.5～5 mm)进行渗流试验。

由于采空区冒落带内破碎岩体的裂(空)隙率大、渗透性强，为强非均质多孔介质，冒落带内破碎岩体中的地下水以垂直运动为主，因此本次研究设计了一套一维渗流砂柱作为渗透性试验装置，该试验装置主要包括供水装置、渗流装置、测压装置和测量装置4部分，如图1所示。

图1 采空区冒落带内破碎岩体渗透性试验装置示意图

该试验装置主体为一总高为1.5 m、内径为20 cm的一维渗流柱，装置从上至下分为上水段、填料段和下水段三部分，每段高度分别为0.25 m、1 m和0.25 m，横截面均一。其中，上水段距离顶端8 cm处开设一孔径为2 cm的溢流孔，以实现定水头入渗；下水段左、右两侧各设一个孔径为2 cm的出水孔，用于控制出水流量；填料段与下水段间铺设一层透水板以支撑充填介质，防止渗透介质掉落，透水板空隙率为45%，填料段进、出水两端各布置一个直径为9 mm的测压孔，用橡胶软管连接至测压管，通过测量装置读取整个渗流段的压力水头。

1.2 试验方法与步骤

为了实现大孔隙非均质渗透介质渗流所需的不同空隙率与变水力梯度，试验过程中通过改变渗透介质的基本粒径与级配粒径的组合比例，取得不同裂(空)隙率的岩体试样，采用常水头稳态渗透法[19]开展渗透性试验，并利用出水阀调节出水流量，控制水头差，实现变水力梯度渗流过程，获得不同裂(空)隙率的岩体试样中地下水水力梯度与渗透流速的时间序列。为了取得较大范围的水力梯度，研究采空区冒落带内破碎岩体中地下水的渗流特征，每组试样设计5个水头差进行渗流试验，建立不同粒径组合试样的压力梯度与渗流速度的关系。具体试验步骤如下：

(1) 将试验材料按不同的体积比进行混合，配制出10组不同空隙率的多孔介质，独立开展渗流试验。不同颗粒级配的采空区冒落带渗透介质试样配比方案，见表1。

表1 不同颗粒级配的采空区冒落带渗透介质试样的配比方案

(2) 采用分层填筑、逐层压实的方法进行填料装填，各分层高度均为10 cm，共分10次，每层装填完记录各材料用量。试验前，需对试验装置的密封性与管路的畅通性进行检验，并对仪器进行校准，确认装置与仪器正常后，打开水阀，采用自底部向上层逐层饱和的方法对试验装置进行注水。待填料段多孔渗透介质达到饱和，且两端水头压力与单位时间出流量均达到稳定值时，定时记录压力值与出水流量。每个固定水头差进行3次连续测量，出流量相对差值不超过1%视为有效数据，计算时采用3次测量的平均值。

(3) 改变水头差后重复进行试验，每组试样进行5个水头差的渗流试验。每组渗流试验结束后，关闭进水阀，打开出水阀，放空并记录渗流段内全部水量，并计算每组渗透介质试样的平均裂隙率，其计算公式为

(1)

式中：f为渗透介质试样的平均裂隙率(%)；V水为渗流段内水量(mL)；V为渗流段体积(m3)。

2 试验结果与分析

2.1 采空区冒落带内破碎岩体的渗流特征

通过采空区冒落带内破碎岩体渗流试验，得出10组不同裂(空)隙率的渗透介质试样中地下水的水力梯度与渗透流速试验数据。本次研究分别利用线性关系式、Izbash公式和Forchheimer公式[20]对采空区冒落带内大孔隙破碎岩体中地下水的混流运动进行描述，见图2。

图2 采空区冒落带内10组不同连通裂(空)隙率渗透介质试样中地下水水力梯度与渗流速度的拟合关系曲线

采空区冒落带内10组不同连通裂(空)隙率渗透介质试样中地下水水力梯度J与渗透流速v的拟合方程及其决定系数R2，见表2。

通过分析图2和表2可以看出：

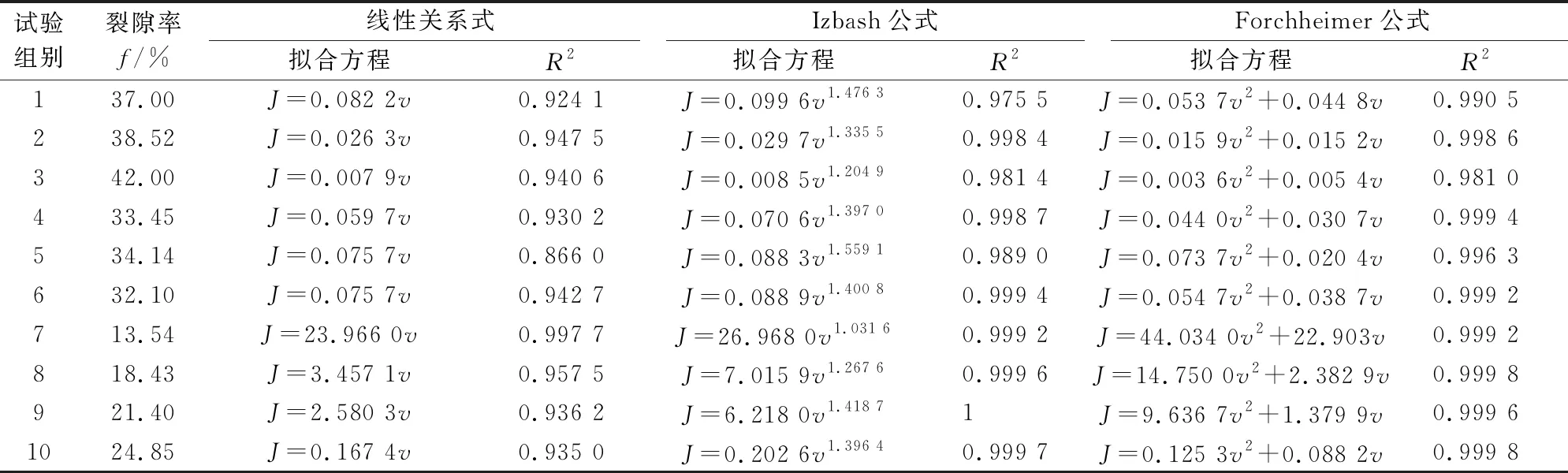
表2 采空区冒落带内10组不同连通裂(空)隙率渗透介质试样渗流试验结果的拟合关系表

(1) Izbash公式、Forchheimer公式与线性关系式相比较，均能更好地拟合冒落带内大孔隙堆积岩体中地下水水力梯度与渗流速度之间的关系，说明采空区冒落带内破碎岩体中地下水流符合高速非线性流。

(2) Izbash公式中的非达西系数n大体上随渗透介质裂隙率的减少而减小。在第7组渗透试验中，破碎岩体的裂隙率最小(13.54%)，且粒径分布范围广，此时非达西系数n为1.031 6，最接近于1，破碎岩体中地下水流运动非常接近达西流，岩体渗透系数K为0.041 cm/s，这表明冒落带内破碎岩体中的地下水流态明显受破碎岩体裂隙率的影响。

2.2 采空区冒落带内破碎岩体渗透系数与裂隙率的关系

Izbash公式和Forchheimer公式都能较好地描述采动岩体内地下水的非达西流。鉴于两者可以互相转化[21]，且Izbash公式变形后的幂函数方程表达式是达西定律的延续[22]，能够直观地体现岩体渗透系数K；而Forchheimer公式为二次多项式，其中各项常数为渗透介质性质与流体性质的函数，不能直接地表征岩体渗透系数值。因此，为了便于确定岩体渗透系数，本次研究采用Izbash方程的变形公式即幂函数方程的拟合结果，可得到采空区冒落带内10组不同连通裂(空)隙率渗透介质试样的渗透系数K，见表3。

由表3可以看出：

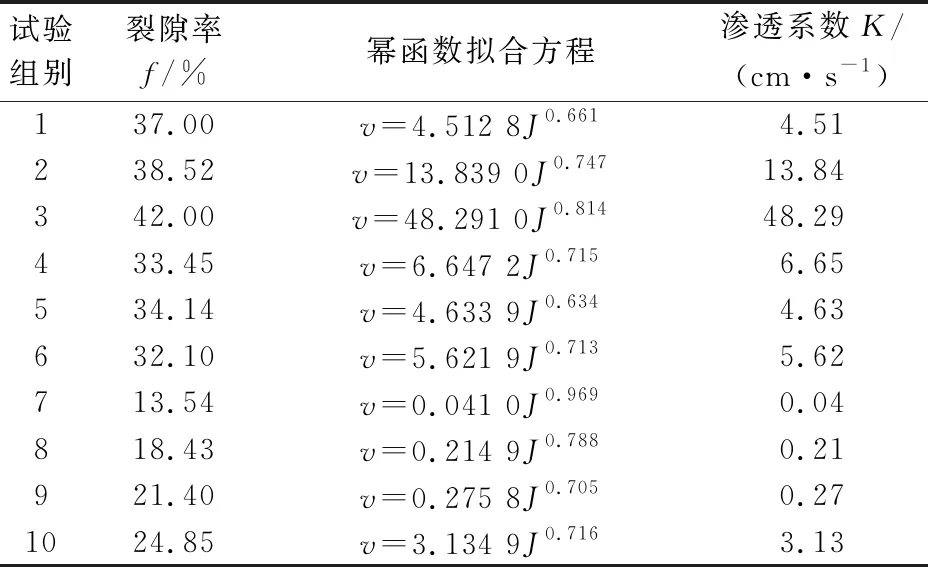
表3 采空区冒落带内10组不同连通裂(空)隙率渗透介质试样的渗透系数表

(1) 冒落带内破碎岩体的裂隙率越小、颗粒级配越接近良好，破碎岩体中地下水水力梯度与渗流速度的关系曲线越接近于直线，渗流越接近线性达西流，流态指数m越接近于1。

(2) 对于以单一粒径碎石为渗透介质的前3组试样，破碎岩体的裂(空)隙率相差不大，但其渗透性能的差别明显，造成这一现象的原因主要是由于砂石的粒径是影响渗流流态的一个重要因素。当裂(空)隙率相近时，渗透介质的平均粒径越小，颗粒间空隙越小，连通性越差，渗流阻力越大，因此采空区冒落带内破碎岩体的渗透系数较小；反之亦然。

(3) 混合粒径渗透介质的渗透性能测试结果表明，颗粒分布是影响渗流流态的另一重要因素。

利用表3中数据，对采空区冒落带内破碎岩体渗透系数K与裂隙率f之间的关系进行了拟合。为了得到更好的拟合效果，本次研究采用全程拟合与分段拟合方法分别进行，并选取均方根误差(RMSE)和决定系数(R2)作为模型评价的指标，其拟合结果见图3和表4。

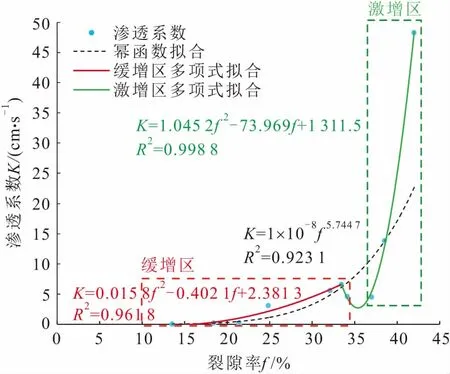
图3 采空区冒落带内破碎岩体渗透系数K与裂隙率f的拟合关系曲线

由图3和表4可知，对采空区冒落带内破碎岩体渗透系数与裂隙率之间的关系采用分段拟合，较全程拟合得到的幂函数回归方程具有更好的拟合效果，因此本次研究选择对采空区冒落带内破碎岩体渗透系数缓增区与激增区进行分段拟合的结果。拟合结果表明：冒落带内破碎岩体的渗透性能总体上随裂(空)隙率的增加而呈现增大的趋势，且随着裂(空)隙率的增大，两者之间的关系是不断变化的。当裂隙率小于30%时，冒落带内破碎岩体渗透性能随裂隙率的增大呈二次多项式函数关系缓慢增长；当裂隙率介于30%～37%时，冒落带内破碎岩体的渗透性能变化不大，渗透系数值集中在5.35 cm/s附近，这是由于部分试样采用不同的碎石粒径组合所获得的裂隙率却相差不大，而破碎岩体的裂隙网络复杂，其裂隙率与渗流流态受块石颗粒的形状、排列、充填情况以及粒径分布、裂隙结构等因素的综合影响，造成岩体渗透系数值随裂隙率增大而变化复杂；单级配小粒径的第1组试样(裂隙率为37%)的渗透性能较弱是由于试样粒径小、渗流阻力大，造成其渗透系数较相近裂隙率的第4、6组试样小，而双级配大粒径的第5组试样(裂隙率为34.14%)所得渗透系数较小考虑是因为试样级配不良且粒径较大，水流作用下反而越容易被压缩，导致孔隙通道发生变化，影响其渗透性能；当裂隙率大于37%时，冒落带内破碎岩体渗透性能与裂隙率之间呈二次多项式函数关系急剧增大。

表4 采空区冒落带内破碎岩体渗透系数K与裂隙率f的拟合参数表

2.3 采空区冒落带内破碎岩体的渗透系数确定

将上述采空区冒落带内破碎岩体渗透系数与裂隙率之间的拟合关系应用于潞安集团常村煤矿S6-9工作面，经工作面观测与相似材料模型试验结果[23]，可得煤层开采结束后该工作面冒落带内裂隙发育区和重新压实区的裂隙率分别为36.89%和14.56%，将裂隙率带入拟合关系模型中，计算得到采动覆岩冒落带内不同位置破碎岩体的渗透系数，见表5。

由表5可知：通过渗透试验所得采空区冒落带内破碎岩体的渗透系数介于0.081～5.167 cm/s之间，这是由于采空区冒落带内不同区域的裂隙发育程度不同，导致破碎岩体渗透系数的差别较大；采空区中部重新压实区破碎岩体的渗透系数明显低于两侧的裂隙发育区破碎岩体；常村煤矿S6-9工作面采空区破碎岩体渗透系数较煤层开采前弱透水性顶板S4砂岩的渗透系数0.000 301 cm/s急剧增大，扩大了3～4个数量级，表明采动破坏对岩石渗透性的影响很大。

表5 采动覆岩冒落带内不同位置破碎岩体的渗透系数

3 结 论

(1) 采空区冒落带内破碎岩体中地下水流呈高速非线性渗流特征，地下水流态受渗透介质的空隙率和颗粒粒径分布的影响，渗透介质的裂(空)隙率越小，粒径分布越广，地下水流越接近达西流。

(2) 采空区冒落带破碎岩体的渗透系数取决于裂隙发育程度，其渗透性能总体上随空隙率的增加而增强。当裂隙率小于30%时，采空区冒落带内破碎岩体的渗透性能随裂隙率的增大缓慢增长；当裂隙率介于30%～37%时，采空区冒落带内破碎岩体的渗透性能变化不大；当裂隙率大于37%时，采空区冒落带内破碎岩体的渗透性能随裂隙率的增大急剧增强。

(3) 采动破坏对岩石渗透性的影响很大，渗透试验结果表明：采空区冒落带内破碎岩体的渗透系数较煤层开采前岩体扩大了3～4个数量级。由于工程实际中冒落带内破碎岩体的体积较模拟试样大，且裂隙更为复杂、丰富，冒落带内破碎岩体中的地下水流将呈更明显的非达西流态。但是，矿山采空区冒落带内破碎岩体的渗流是一个复杂的系统，受现场条件与试验设备的限制，本次研究采用室内渗透性试验对相关条件进行了理想化假设，得出的冒落带内破碎岩体渗透系数与其裂(空)隙率的相关关系可为矿井开采后岩层与地下水的受影响程度评价工作与数值计算所需的岩体渗透特性参数提供数值依据。