基于数据驱动贝叶斯网络的内河船舶交通事故分析

叶子阳，陈沿伊，张培林，程 盼，钟惠林，侯华保

(武汉理工大学交通与物流工程学院，湖北 武汉 430063)

我国水路运输尤其是内河运输领域的投资不断增大，有资料显示2019年内河建设完成投资614亿元，全国内河航道通航里程达到了12.73万km。伴随着我国内河航道通航里程的增长，船舶数量不断攀升，航运事故数居高不下。根据长江海事局通报的相关数据，2020年共发生水上交通事故113起，其中一般及以上等级事故12起，死亡失踪人数21人，造成的直接经济损失约1 702万元，安全监管态势十分严峻。2020年6月，交通运输部发布的《内河航运发展纲要》[1]中指出：要构筑功能完善、能力充分的航运安全体系，完善安全风险防控与监管体系，完善安全生产风险分级管控和事故隐患排查治理双重预防机制，建立完善的安全风险清单。

船舶航行安全是一项复杂的系统工程，它需要综合考虑船舶、航道、气候等多方面的因素。同时，大多数船舶交通运输事故的特点是低概率高后果，对模型的稳定性要求较高[2]。国内外学者针对通航事故安全风险进行了广泛的研究。如：Fan等[3]基于MAIB、 TSC等海上事故报告建立了贝叶斯网络，对海上交通事故关键影响因素进行了分析；Pristrom等[4]利用专家调查法建立了贝叶斯网络，研究了在不确定条件下做出具有成本效益的海上反海盗决策；李振福等[5]在AIS数据的基础上运用云模型和熵权法识别了海区的安全风险。但在内河通航安全风险分析中，学者们较多利用模糊综合评价或证据推理等方法来进行通航安全风险评估。如：王恺[6]建立了单因素模糊评价模型，对无锡运河水域的通航环境进行了分析；郝勇等[7]参考冰山模型理论识别了船员素质对通航安全的影响因素，构建了长江危险品船船员素质评价指标体系；张笛等[8]运用模糊规则库和证据推理相结合的方法对内河通航安全风险进行了评价。此外，一些学者利用贝叶斯网络模型对通航安全风险进行了评估。如李昊等[9]运用贝叶斯网络建立了内河航运安全指数体系，主要是从整体上反映航运安全的变动趋势和程度。而通过数据驱动建立贝叶斯网络，对内河单船在特定风险因素组合下船舶可能发生的事故类型和不同事故类型关键影响因素的研究则较为少见。如Fan等[10]的研究发现，发生落水事故的关键影响因素是船舶类型为渔船，而发生倾覆事故的关键因素是船舶作业类型(拖航)。

考虑贝叶斯网络具有很好的建模随机性和捕捉非线性因果关系的能力[11]，故本文引入贝叶斯网络理论，在芜湖海事局2013—2020年上报的219条内河航运事故船舶数据的基础上，经过数据清理和补全提炼出影响内河船舶航运安全的因素，使用贝叶斯可视化软件Netica进行参数学习，建立内河船舶交通事故的贝叶斯网络模型，并对内河船舶航运安全风险进行正向推理和反向诊断，进而分析得到内河通航船舶的高风险情景和不同事故类型的关键影响因素。

1 贝叶斯网络理论基础

贝叶斯网络是基于图论和概率论，将先验知识与样本数据有机结合来对不确定性问题进行模拟和推理的一种有效工具，它需要经过结构学习、参数学习和推理分析来获得解决问题的依据[12]。

1.1 贝叶斯定理

在通常情况下，事件A在事件B发生条件下的概率和事件B在事件A发生条件下的概率是不一样的，贝叶斯网络就是基于概率理论对这种关系的陈述。P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率，其基本求解公式如下：

P(A|B)=(P(AB))/(P(B))

(1)

其中，A和B代表基本事件集E中的两个事件。

对于事件A1，A2,…,An，且P(A1)≥P(A1,A2)≥…≥P(A1,A2,…,Pn-1)，可推导出乘法式如下[13]:

P(A1A2…An)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1)

(2)

后验概率公式就是贝叶斯网络的推理基础。设先验概率为P(B1)， 若条件概率P(Aj|Bi)已知，且P(Bi)>0，则贝叶斯后验概率公式如下：

(3)

1.2 贝叶斯网络建模

贝叶斯网络的结构是一种有向无环图(E,A)，其中节点E={E1,E2,…,En}用来表示变量，各变量之间的相互关系则用有向弧A表示，有向弧的方向是从原因节点指向结果节点，即父节点指向子节点，而没有直接链接的节点表示有条件地相互独立。贝叶斯网络的参数θ是代表变量间相互关系的条件概率表(Conditional Probability Table，CPT)，用P(Ei|Pa(Ei))表示，代表变量之间的相互依赖关系[21]。换言之，贝叶斯网络是由各节点间具有相互依赖关系的网状结构和变量之间相联系的条件概率表组成，对于有向边(Ei,Ej)，Ei的父节点用Pa(Ei)表示，非后代节点可用A(Ei)表示。在给定父节点的条件下，非后代节点与父节点Ei条件独立[14],即：

P(Ei|Pa(Ei),A(Ei))=P(Ei|Pa(Ei))

(4)

则联合概率为[15]

(5)

因此,贝叶斯网络节点的选择是确定贝叶斯网络结构的先决条件，在确定贝叶斯网络结构后，就应对其节点的相关参数进行学习。贝叶斯网络参数学习共有两种方式：一是基于专家经验，通过发放问卷的方式获得相关变量的权重，并通过计算获得各个节点的条件概率表；二是利用数据驱动，通过导入相关事故数据来训练模型，以获得相关节点的条件概率。本文选用第二种方法，基于船舶航运事故数据进行参数学习。就数据驱动方法而言，也有许多种不同的方法，如朴素贝叶斯网络(NBN)算法、树增强型朴素贝叶斯网络(TAN)算法，考虑到本模型各影响因素之间的相互影响较小，朴素贝叶斯网络算法对于给出的待分类项会选择条件概率最大的类别，且具有建模简单、鲁棒性较强等特点，故本文拟定采用朴素贝叶斯网络建模。

同时，由于采用具有唯一子节点的朴素贝叶斯网络结构(见图1)，目标节点的条件概率表将会非常庞大，进行参数学习时会作为模型变量极大地增加工作量。因此，考虑到贝叶斯网络具有双向风险分析的能力，为了简化结构，本文提出了一种改进的发散朴素贝叶斯网络结构。该结构将目标节点当作唯一的父节点，其余影响因素均作为该父节点影响下的子节点(见图2)，这种结构可以在很大程度上减少条件概率的计算量，且对最终的结果没有影响[10]。

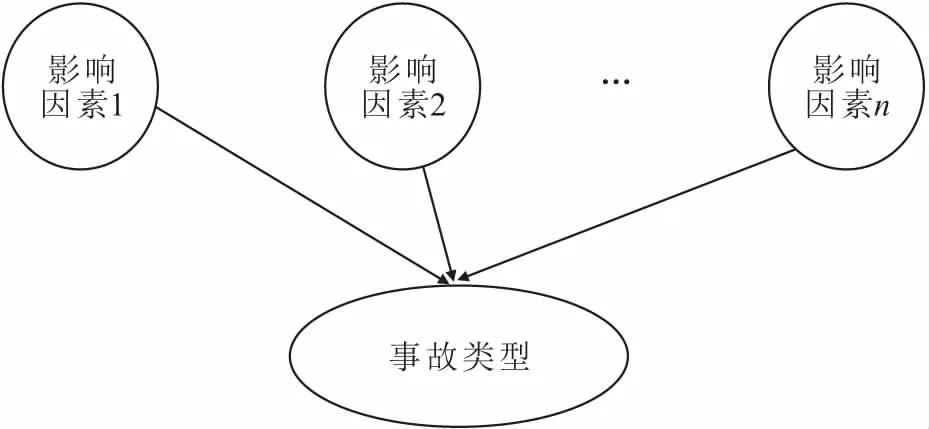
图1 朴素贝叶斯网络结构(唯一子节点)

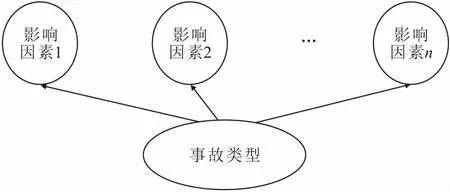
图2 改进的发散朴素贝叶斯网络结构(唯一父节点)

综上所述，基于数据驱动的朴素贝叶斯网络建模流程，见图3。

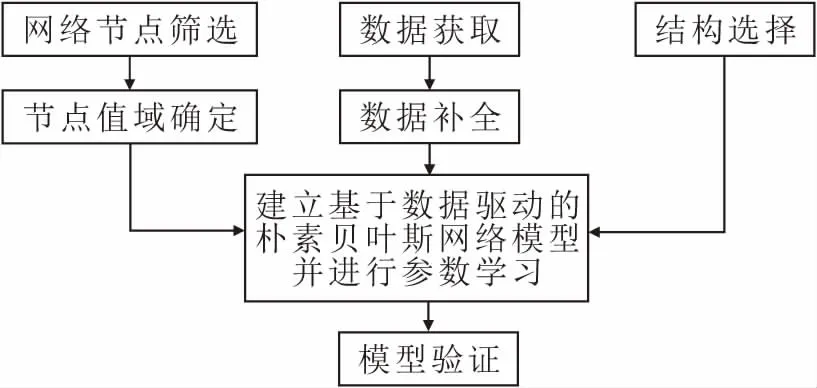
图3 基于数据驱动的朴素贝叶斯网络建模流程图

2 内河船舶交通事故的贝叶斯网络模型构建

2.1 网络节点及其值域的确定

本文基于芜湖海事局内河航运事故数据库(包含上报及未上报数据、事故报告等)，参考相关文献[16-17]以及内河通航管理规范[18]，在确定节点名称时从航道、气候和船舶三个方面的影响因素展开，共提炼出与内河船舶通航安全关联较大且较易被海事局等部门识别的的16个影响因素作为模型变量，包括是否桥区、是否弯曲航道、航行密度、航道水深富裕程度、航道宽度富裕程度、是否下雨、是否雾天、风力、昼夜、水期、船舶类型、船舶归属、船龄、是否满载、航行方向、船员配备。其中，考虑到水流流速也是一个能够客观反映内河船舶通航安全状态的指标，但该指标是实时动态变化的，较难获得，故选用综合性指标“水期”代替。但是，“水期”反映的是事故发生时的整体航道水流状况，且不能完全等同于“航道水深富裕程度”，因为“水期”是一个相对客观的评判，而“航道水深富裕程度”则与船舶本身的性质有着很大的关系。

在本文选取的16个变量中，部分变量状态如昼夜、是否下雨、是否起雾和航行方向等的定义可以从芜湖海事局上报的船舶航运事故数据库中得到，这些变量状态的定义也在各类参考文献中被广泛接受。但也有一些变量状态如船舶类型、是否满载等是结合相关文献和长江下游芜湖航段的船舶通航事故总结得出，如长江下游芜湖航段的事故船舶类型包括干散货船、件杂货船、危险化学品运输船、拖轮、驳船、集装箱船、渔船、工程船等，结合芜湖海事局上报的航运事故船舶类型数据统计可以发现件杂货船、渔船、工程船、驳船等船舶类型数量较少，考虑到样本容量和模型的准确度问题，本文将这些船舶类型统称为其他船舶。关于内河船舶交通事故16个影响因素的定义，详见表1。

表1 内河航舶交通事故影响因素的定义

由于贝叶斯网络模型涉及多个维度的不同节点，为了全面、客观地反映不同节点对子节点的影响，参考相关文献及专家经验，本文将节点的值域用离散型变量展示，不同的父节点有着不同的值域。而对于最终的子节点，本文结合实际情况将事故类型分为碰撞(collision)、触碰(contact)、火灾(fire damage)、搁浅(grounding)、自沉(sinking)和其他(others)6种。

通过对长江海事事故的分析发现，内河船舶交通事故不同评价指标的危险系数不同，例如：水期影响因素的危险系数表现为枯水期>洪水期>中水期[19]；不同类型的船舶评价指标危险系数也不一样，如集装箱船一般较为坚固耐用，而危险品及油船等属于交管部门严加管控的对象[16]。因此，本文根据内河船舶交通事故不同影响因素的危险系数对各影响因素进行了重新分级，具体等级划分标准见表2。

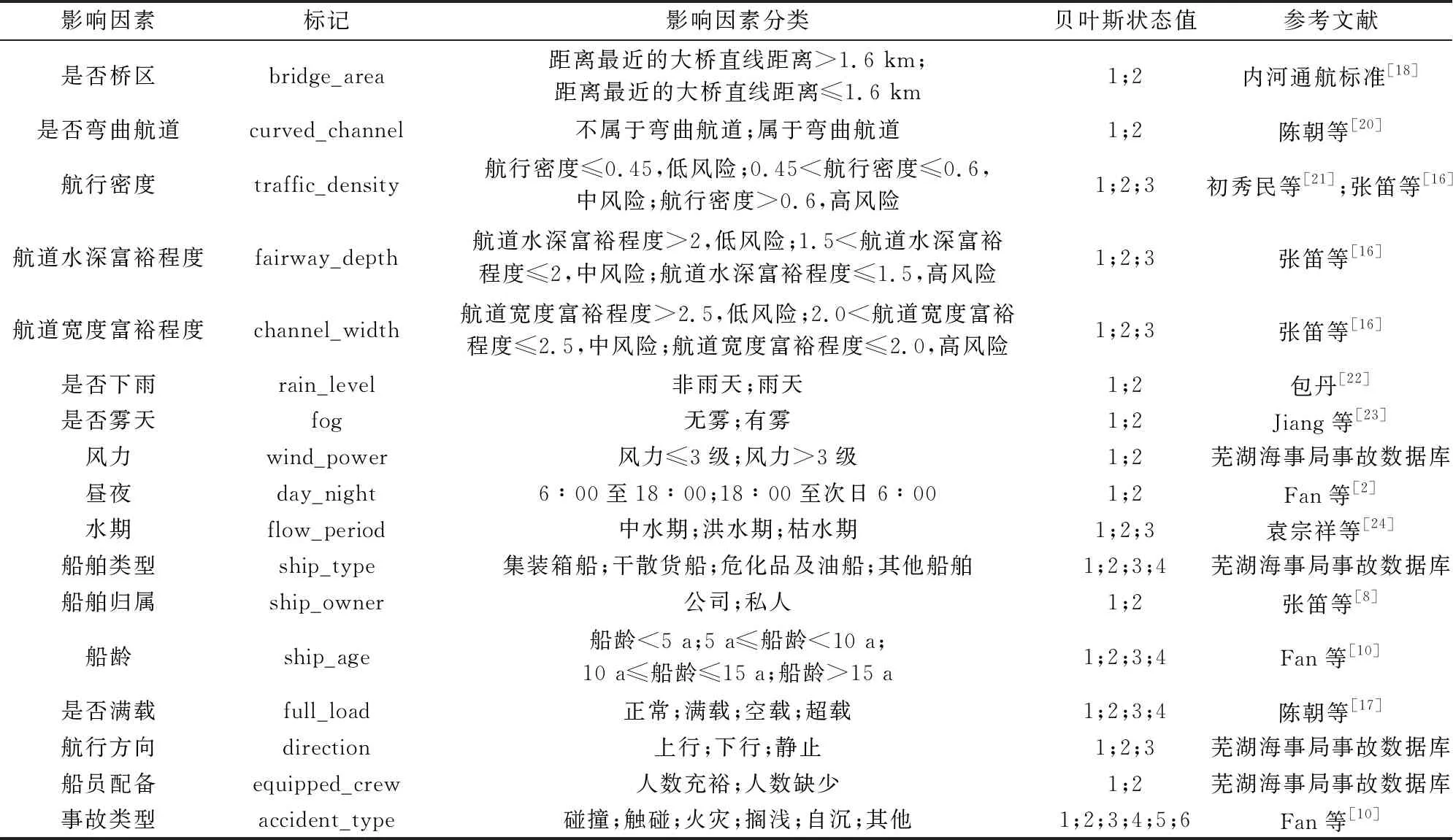
表2 内河船舶交通事故影响因素等级划分标准

2.2 数据采集及获取

本模型事故数据来源于芜湖海事局2013—2020年度上报的所有内河船舶交通事故数据库，通过对该数据库中的数据进行筛选，重点是剔除与船舶通行无关的诸如游客戏水导致的事故以及部分发生在小型渔船上由于某些特殊原因导致的事故等数据，最终共选取最近8年具有代表性的内河船舶交通事故数据159条，事故船舶数据219条。由于芜湖海事局上报的内河船舶交通事故数据库中存在部分影响因素无法提取和信息缺失的情况，故本文广泛运用船讯网、长江海事局官网、长江航道局电子航道图等资料进行数据补充，最终构造出本文数据库。

此外，考虑到不同类型的船舶具备不同的船舶特性，因此本文以事故船舶数据为基础，随机抽取154条事故船舶数据作为组建事故类型预测分析的训练样本，65条事故船舶数据用于作为事故类型预测的验证样本。

2.3 贝叶斯网络拓扑结构的确定及参数学习

本文基于芜湖海事局上报的内河船舶交通事故数据为基础，考虑构建基于朴素贝叶斯网络的内河船舶交通事故预测模型。由于各影响因素之间并不完全独立，但参考相关文献，也没有证据证明这些影响因素之间具有较强的相关性[9-10,17]，且已有研究表明这种假设并不会显著影响贝叶斯网络建立后各节点的条件概率[12]，而且对之后情景分析的影响也更为有限，因此可视为各影响因素独立。综上，可在此假设的基础上建立朴素贝叶斯网络(见图4)，此时事故类型是唯一的父节点，其余各子节点也就是原始的各影响因素如是否桥区、航行密度、水期、船舶归属以及是否满载等相互独立。

图4 内河船舶交通事故的朴素贝叶斯网络模型

在确定贝叶斯网络结构后，基于内河船舶交通事故船舶数据，在建立的内河船舶交通事故朴素贝叶斯网络预测模型的基础上，通过贝叶斯可视化软件Netica对模型中的关键节点进行参数学习，而一旦条件概率表被构建与获得，就可以计算每个影响因素的后验概率。该模型的训练结果见图5。

图5 内河船舶交通事故的贝叶斯网络模型训练结果

3 贝叶斯网络模型结果验证及情景分析

3.1 贝叶斯网络模型结果分析及验证

3.1.1 贝叶斯网络模型结果分析

涉及航道因素、气候因素、船舶因素的16个影响因素的内河船舶交通事故贝叶斯网络模型的训练结果，见图5。

由图5可以看出：

(1) 就事故类型而言，2013—2020这8年间长江下游芜湖海事局所辖航道发生的船舶交通事故以碰撞事故(collision)为主，该事故发生概率高达54.1%，而发生触碰、火灾、搁浅和自沉和其他事故的概率差别不大，在6.9%～13.7%范围内。

(2) 就航道因素而言，14.1%概率的事故发生在桥区航道，弯曲航道发生事故占比接近一半，为49.8%；芜湖海事局所辖航道船舶航行流量较大，事故发生在航行流量高峰期的概率约为43.7%，事故发生在航行流量中峰期的概率为50.8%，两者占比达94.5%；33.8%概率的事故发生在航道水深富裕程度高风险时期，在该时期航道水深和吃水的比值均小于1.5；只有约4.2%概率的事故发生在航道宽度富裕程度不足的时期，而剩下95.8%的事故发生在航道宽度富裕程度充足(即低风险)和航道宽度富裕程度中等(即中风险)时期，但这并不能说明航道宽度富裕程度不足时船舶航行安全系数较高，这是由于目标航段的航道宽度普遍较大，航道宽度对内河船舶航行事故特别是碰撞事故的影响较小。

(3) 就气候因素而言，43.5%概率的事故发生在雨天，38.5%概率的事故发生在风力大于3级的场景下；事故发生时间对事故也有一定的影响，63.8%概率的事故发生在18∶00至次日6∶00，可见夜间船舶航行的风险较高；而就水期而言，枯水期发生事故概率约为24.9%，洪水期发生的事故概率比达43.1%；由于目标航道地处长江中下游，雾天相对较少，且海事局等部门往往会采取禁航等措施来限制雾天航行，因此发生在雾天的事故占比仅为7.3%。

(4) 就船舶因素而言,干散货船发生事故的概率较高，达到了69.4%；个体所有的船舶发生事故概率接近一半，为48.0%；船舶船龄大于15 a发生事故的概率约为9.8%，船舶船龄10～15 a发生事故的概率大约为14.9%；船舶航行方向为上行、下行状态时发生事故的概率接近，均超过40%，其余为静止状态；船舶超载和空载发生事故的概率分别占28.2%和25.1%。

3.1.2 贝叶斯网络正向推理

基于生成的朴素贝叶斯网络，可根据目标节点事故类型，结合事故概率分布变化逆推子节点影响因素的重要性。当调整搁浅事故(grounding)的发生概率至100%时，发现变化幅度最大的几项影响因素依次为航行方向、是否弯曲航道、航道水深富裕程度和是否下雨(见图6)，即表明船舶在雨天下行时，其通过航道深度不足的弯曲航道时极易发生搁浅事故。

图6 内河船舶搁浅事故贝叶斯网络模型的结果

同理，当调整碰撞事故(collision)的发生概率至100%时，发现当船龄较大的船舶夜间通航于枯水期且当时风力等级较高时极易发生碰撞事故。通常情况下航行密度和航道是否弯曲对碰撞事故的概率也会造成一定的影响，但本文的目标航段处于长江中、下游地区，航道条件相对较好，即使航道处于流量高峰期或者航道较为弯曲时，也有足够的航道富裕宽度，因此航道本身的因素对碰撞事故发生概率的影响较小，但随着航道的上溯，当航段处于长江上游地区时，航行密度、航道是否弯曲对碰撞事故的影响也会随之增大。同理，可以推测出火灾、触碰、自沉和其他内河船舶交通事故类型的主要影响因素，见表3。

表3 内河船舶不同交通事故类型的主要影响因素

3.1.3 贝叶斯网络模型验证

本文对219条样本数据按照事故类型分布进行分层随机抽样，选用训练样本154条(70%)，验证样本65条(30%)，并利用贝叶斯可视化软件Netica对样本进行训练，得到如图5所示的贝叶斯网络模型训练结果。

为了验证建立的朴素贝叶斯网络模型对样本预测的准确率，本文调用Python程序对该事故船舶数据集进行验证，经正向验证发现该模型预测的准确率为75.4%，表明该模型具备一定的参考性。验证样本事故类型分布，见表4。

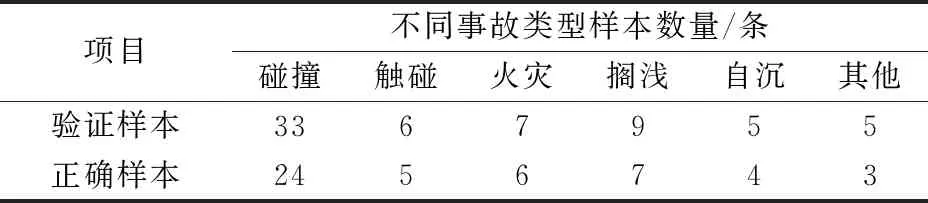
表4 验证样本事故类型分布

同时在Python程序中，本文针对该数据集基于朴素贝叶斯网络模型进行了100次训练，每次均随机选用70%作为训练样本、30%作为验证样本，其验证结果见图7。

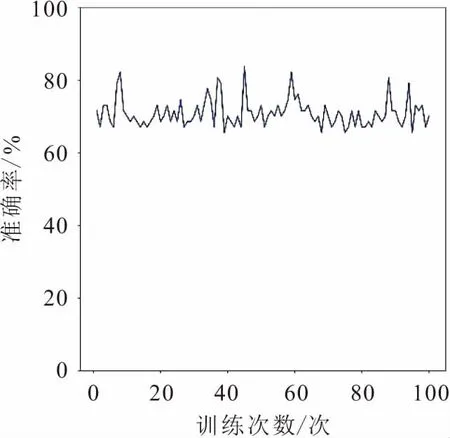
图7 基于朴素贝叶斯网络对数据集预测准确率的验证结果

由图7可见，基于朴素贝叶斯网络模型对数据集预测的准确率基本维持在65%～84%之间，表明朴素贝叶斯网络模型针对该数据集的预测精度具备较好的稳定性。

3.2 情景分析

考虑到贝叶斯网络模型具备动态分析的功能特点，其适用于分析在涉及船舶运行特征和环境因素等不同情景下各种事故类型发生的可能性。因此，本文通过设置多个影响因素同时变动的四个复合场景，用以判断在不同场景下最有可能发生的事故类型，并找出该事故类型对应的主要影响因素，以为海事局等部门制定相应的防控措施提供理论支持。

3.2.1 环境因素变动

环境因素主要包含航道和气候两个方面的因素，具体包含是否桥区、是否弯曲航道、航行密度、航道水深富裕程度、航道宽度富裕程度、是否下雨、是否有雾、风力等级、昼夜和水期10个影响因素。

情景一：当将环境因素节点分配到如图8所示的状态时，碰撞(collision)事故的发生概率增长了约22个百分点，达到了76.2%；同时发生触碰(contact)事故的风险也比常规情况提升了近一倍，达到了16.5%。也就是说，当目标船舶在洪水期风雨交加的夜间(即18∶00至次日6∶00)驶入弯曲航道且船舶航行密度较大时，最容易发生碰撞和触碰事故。

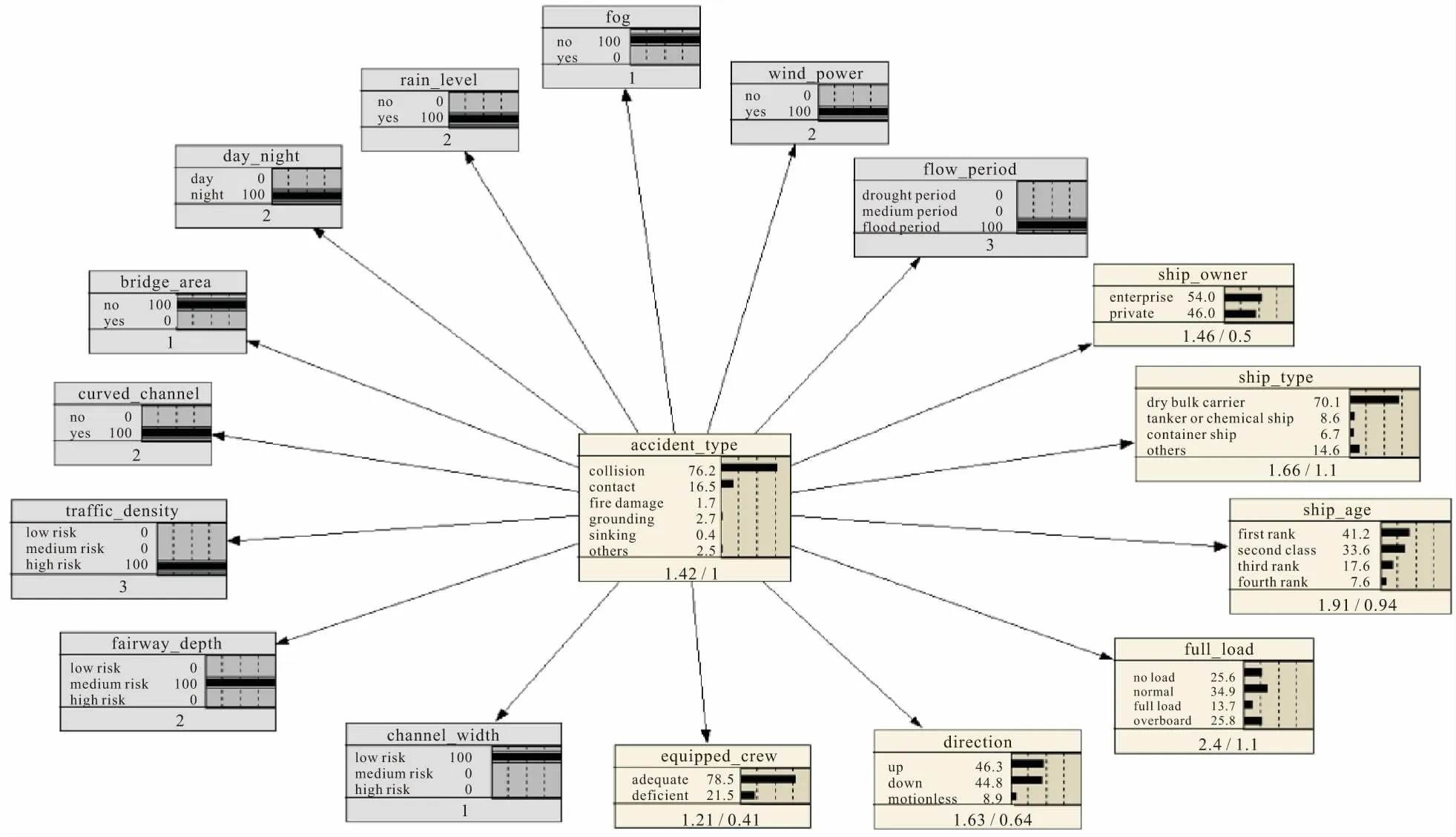
图8 内河船舶交通事故的贝叶斯网络模型(情景一)

情景二：当将环境因素节点分配到如图9所示的状态时，搁浅事故成为发生概率最大的事故类型，发生事故且为搁浅事故的概率由原来的13.7%骤升至88.3%，而除碰撞事故外其他事故发生的概率均小于1%。因此，当枯水期无风无雨有雾的白天(即6∶00至18∶00)，航道水深富裕程度和航道宽度富裕程度均处在高风险，且船舶航行密度正常时，在弯曲航道非桥区通航的船舶更容易发生搁浅事故，故海事局等部门应做好有针对性的预警工作。

图9 内河船舶交通事故的贝叶斯网络模型(情景二)

3.2.2 船舶因素变动

此外，本文还考虑了船舶因素变动对内河船舶交通事故类型的影响，船舶因素包括6个影响因素，分别是：船舶归属、船舶类型、船龄、航行方向、是否满载和船员配备，这也是内河船舶一些比较突出的特征。

情景三：当将船舶因素节点变动到如图10所示的状态时，即公司制的集装箱船舶、船龄偏大且空载静止的条件下，火灾(fire_damage)事故的发生概率最高，同比该事故发生的概率增长了67.7%，从原有的9.6%增长到如今的77.3%，此时第二种可能发生的事故类型仍为碰撞(collision)事故，不过该事故发生的概率下降了约41.9%。

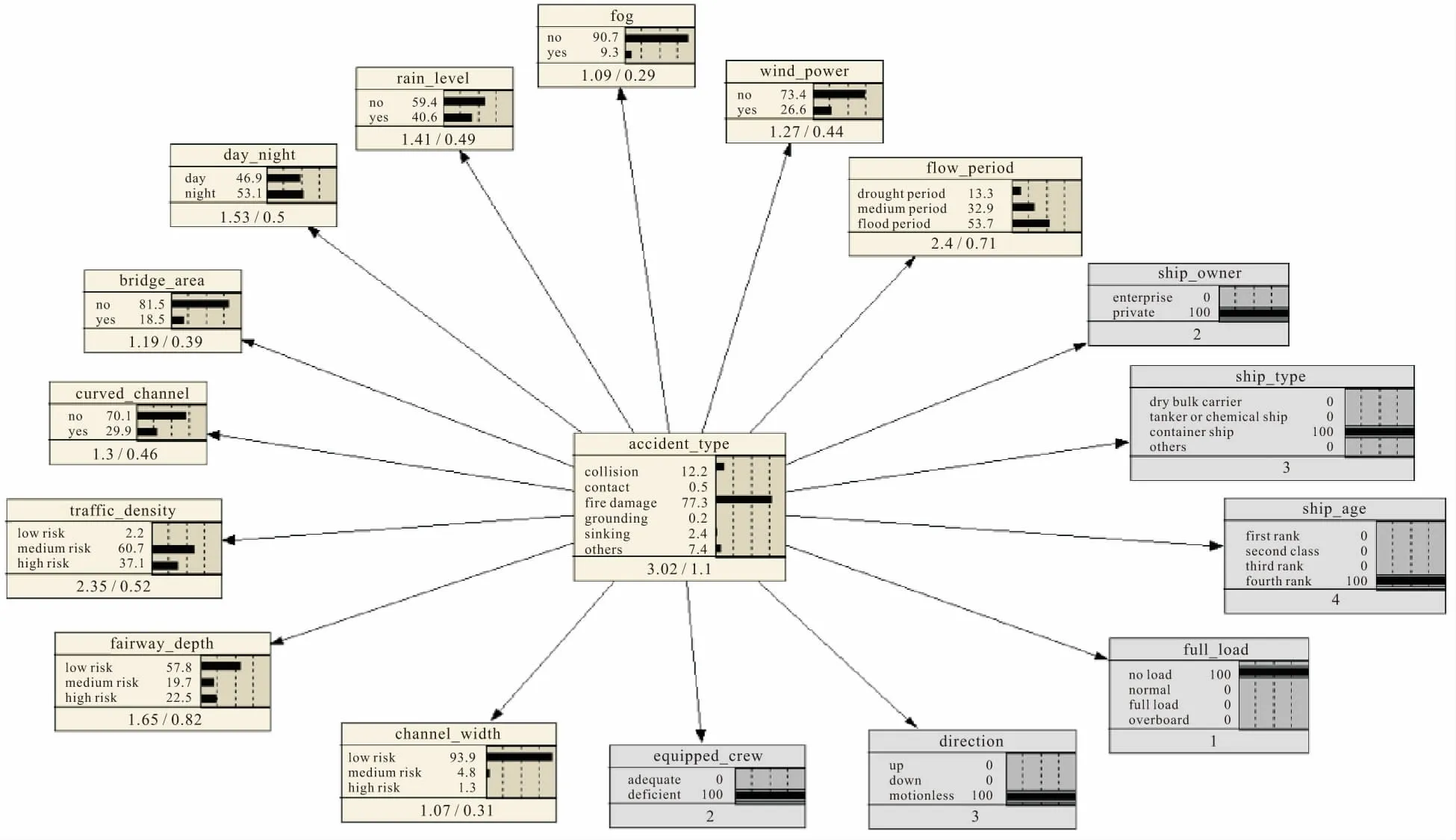
图10 内河船舶交通事故的贝叶斯网络模型(情景三)

情景四：当将船舶因素节点变动到如图11所示的状态时，自沉事故的发生概率最大，同比其事故发生概率增长了约59.6%，此时第二种可能发生的事故类型为碰撞事故，同比其事故发生概率下降了约33.1%，说明船龄、航行方向、船舶类型等的变动，对事故类型的变动有着较大的影响。由图11分析可知，当船龄较大的个体所有小船处在下行超载的情况下非常容易发生自沉事故，故应做好有针对性的预案工作。

图11 内河船舶交通事故的贝叶斯网络模型(情景四)

4 结 论

本文结合芜湖海事局2013—2020年间的内河船舶交通事故上报数据，通过对影响内河通航安全因素的分析，建立了一个基于朴素贝叶斯网络的内河船舶交通事故模型，相比现有多集中于事故发生可能性及严重程度的研究，本文完全基于数据驱动的方法，对可能发生的事故类型进行预测，在最大程度上减少了人为主观因素对预测结果的影响。通过对模型展开原因分析，同时设置情景分析得出了如下结论：

(1) 模型展现出长江中、下游芜湖航段的船舶交通事故以碰撞事故为主，碰撞事故的先验概率超过了50%，其余事故类型的发生概率较小，在通常情况下海事局等部门应针对碰撞事故采取有针对性的预防措施。同时贝叶斯网络结构显示目标航段航道宽度、雾天等节点对内河船舶发生交通事故的影响较小，符合目标航段地处长江下游的航道及其气候特点。

(2) 通过对各种不同事故类型展开分类分析，并通过后验概率的变化得出不同事故类型在目标航段所对应的关键子节点。碰撞事故的关键子节点为船员配备、昼夜、水期和风力；触碰事故的关键子节点为航行密度、航行方向、水期和是否桥区；火灾事故的关键子节点为船员配备、航行密度、船龄和航行方向；搁浅事故的关键子节点为航行方向、是否弯曲航道、航道富裕水深和是否下雨；自沉事故的关键子节点为船龄、船舶类型、是否弯曲航道和航行密度；其他事故的关键子节点为是否满载、昼夜、船舶类型和风力。经走访调查，本模型针对不同事故类型关键子节点的提取基本符合芜湖海事局所辖航段的事故特征。如：当航行密度较高且为桥区时，的确更容易发生触碰类事故；而当处于枯水期，航道水深富裕程度为高风险时，由于水位较低更容易发生搁浅事故。可见，本模型预测结果与客观实际情况较为吻合，具备较高的参考价值。

(3) 环境因素变动下的情景分析通过预设两种不同的情景，揭示了不同航道因素和气候因素共同作用下对事故类型造成的影响。当船舶通航环境处于以下状态时，碰撞事故发生的概率最高：高通航密度、弯曲航道、夜间、雨天、风力大于3级；当船舶通航环境处于以下状态时，搁浅事故发生的概率最高：航道水深富裕程度为高风险、航道宽度富裕程度为高风险、航行密度中等、弯曲航道、非桥区航道、白天、无雨、有雾、风力小于等于3级、枯水期。

(4) 船舶因素变动下的情景分析同样通过预设两种不同场景，展现了不同船舶因素共同作用下对事故类型造成的影响。当船舶自身通行状况处于以下状态时，火灾事故发生的概率最高：个体所有船舶、集装箱船、船龄大于15 a、空载、航行方向处于静止状态、船员配备不足；当船舶自身通行状况处于以下状态时，自沉事故发生的概率最高：个体所有的船舶、渔船等小型船舶、船龄大于15 a、超载、航行方向处于下行状态、船员配备不足。

本文共提取16个最易被海事管理部门侦测的影响因素，方便海事管理部门对特定情境下船舶可能发生的事故类型进行快速预判，并通过建立的朴素贝叶斯网络模型针对任意目标船舶动态调整相应的参数，判断出目标船舶最可能发生的事故类型，从而采取相应的控制措施将事故发生的可能性降到最低。但由于受限于样本数量较少及上报数据库信息不够完善等问题，本模型的结构还有一定的改进空间，后期可以考虑增加完整的事故报告或添加人为因素判定来弥补现有数据的不足，完善现有模型以提高模型预测的准确率以及处理其他复杂性问题的能力。