粗糙云模型与PROMETHEE的航发主轴轴承失效模式重要度评估

牛凯岑，邱明*,,2，李军星，许艳雷，李燕科

（1.河南科技大学机电工程学院，河南洛阳471003；2.机械装备先进制造河南省协同创新中心，河南洛阳471003）

主轴轴承是航空发动机稳定可靠运行的核心部件，长期工作在高速、高温的工况条件下，随着航空发动机的不断升级，推重比不断提高，使得主轴轴承的工作条件变得更加苛刻，容易出现失效导致航空发动机不能正常工作，甚至导致严重的安全事故[1]。主轴轴承的故障率较高且损伤模式多种多样，因此对其进行故障模式及影响分析（FMEA）具有重要的意义。

FMEA 最早是由美国航空航天行业提出的一种系统性、结构性方法，用来保障系统运行的可靠性和安全性[2]。传统的FMEA 从发生频率（O）、严重程度（S）和可探测程度（D）这3个方面对各个潜在故障模式进行评价，以三者的乘积（RPN）作为故障模式重要程度的评判标准。但传统的FMEA 存在着一些缺陷[3]：1）不同的O、S、D 可能得到相同的RPN值；2）没有考虑风险元素的权重；3）各风险元素的度量具有较大的主观性、模糊性等。

为解决上述问题，国内外学者做了大量关于改进FMEA 方法的研究，将FMEA 方法与其他系统可靠性方法相结合，包括故障树分析（FTA）、事件树分析（ETA）等。张红旗等[4]将改进FMEA 与故障传播模型相结合，提出了一种新的混合故障诊断方法；张蓉和王春洁[5]结合FMEA 与FTA，运用蒙特卡洛原理计算系统可靠性指标。运用二元语言模型、直觉模糊集理论、粗糙集理论、云模型理论等方法降低专家评价信息中的主观性与模糊性。崔文彬等[6]将模糊综合评判与FMEA 理论相结合，对船舶喷水推进器液压系统进行安全评估；耿秀丽等[7]提出了一种基于模糊集的改进FMEA 方法；Wang 等[8]提出了一种基于云模型的水质评价方法；张彦如等[9]将粗糙集理论与田口质量观相结合，对发动机装配过程的失效模式进行评估；

同时FMEA 的失效模式风险排序本质上是一个多准则决策（MCDM）问题[10]。越来越多的MCDM方法被应用到对FMEA 方法的改进研究中，如灰色关联分析（GRA）、逼近理想解排序（TOPSIS）、决策试验和评价实验室（DEMATEL）、偏好顺序结构评估（PROMETHEE）和复杂比例评估（COPRAS）等。杜晗恒和彭翀[11]运用模糊语言变量与TOPSIS对数控系统的故障模式进行风险排序；Rashidi 等[12]开发了一种基于模糊集理论分级TOPSIS 方法；李元斌等[13]运用熵权法确定风险指标的信息熵权，利用改进熵权TOPSIS法更准确快速地评估限寿件故障模式的危害程度。Liu 等[14]提出了一种云模型与分层TOPSIS相结合的方法；Huang等[15]在此基础上将粗糙集理论应用其中，更好的反映了专家评价信息的模糊性与随机性。鞠萍华等[16]运用多粒度概率语言术语集（PLTS）刻画了专家评估信息的多样性和不确定性，运用最优最劣法（BWM）和熵权法相结合的综合赋权法确定风险因子权重，将PROMETHEE拓展到概率语言环境中用于确定故障模式风险优先序；MAITY 和CHAKRABORTY[17]提出了一种基于云模型理论与PROMETHEE的改进FMEA 方法，对工具钢材料的性能进行了评价，解决工具钢材料的选择问题。

基于上述情况，提出了一种基于粗糙集理论、云模型理论与PROMETHEE的改进FMEA 方法，对航空发动机主轴轴承的6种失效模式进行重要度评估。首先，通过专家系统构建航发主轴轴承失效模式的风险评估矩阵，运用粗糙集理论、云模型理论，将其转化为粗糙云评估矩阵，描述专家评价信息中的主观性、模糊性和随机性问题。其次，运用统计学方差的思想计算RPN 元素的客观权重，综合专家与RPN 元素的客观、主观权重，建立加权粗糙云评估矩阵。同时，通过PROMETHEE 法计算各风险元素的流出量、流入量与净流量，根据净流量大小对航发主轴轴承的失效模式进行风险排序。最后，结合航发主轴轴承失效模式分析工程实例，对本文方法进行验证与对比分析。

1 粗糙云模型的FMEA 建模

1.1 失效模式分析

综合航空发动机主轴轴承的运行工况与工作特点，由专家小组确定其主要潜在失效模式，分析其形成原因与预防措施。设有L个专家（TMk，k = 1，2，···，L）、m个失效模式（FMi，i=1，2，···，m）和n个RPN元素（Rj，j =1，2，···，n），构建FMEA 结构模型，专家成员对不同RPN 元素下的轴承失效模式进行评价，得到专家成员TMk的风险评估矩阵Vk=()，其中vkij代表成员TMk对第j 个RPN 元素下第i 个轴承失效模式的评价值。语言术语集如表1所示。

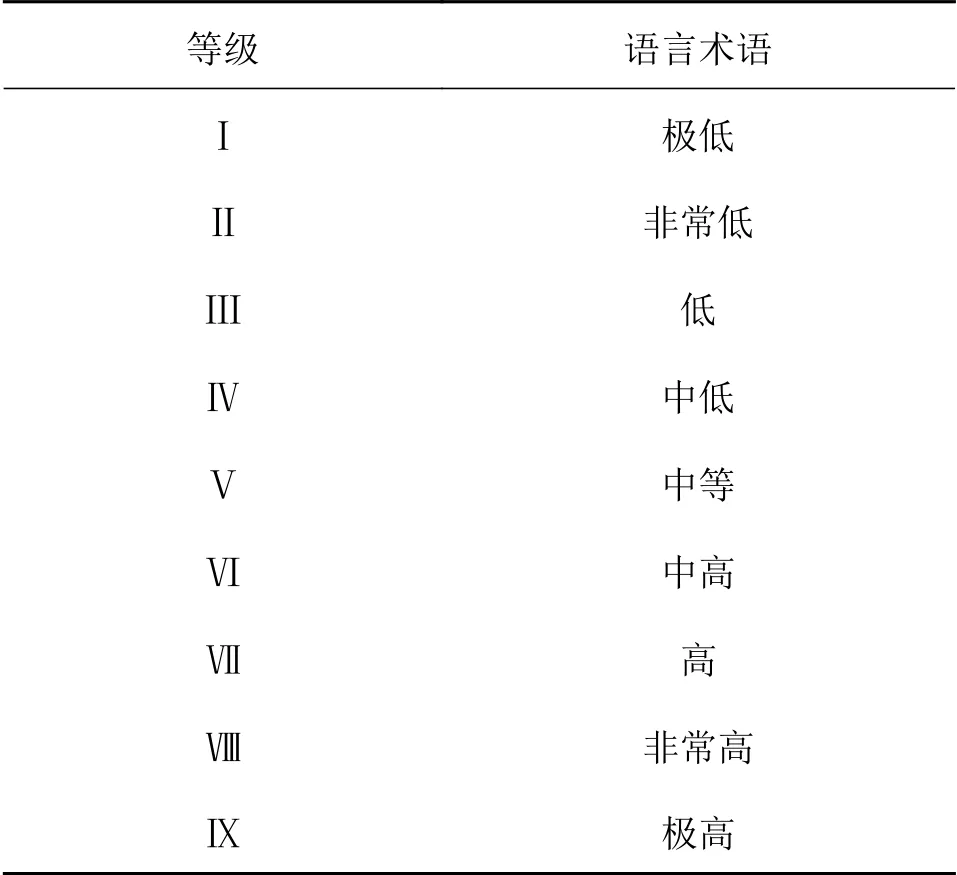
表1 语言术语集

1.2 粗糙集评估矩阵模型

粗糙集是处理不精确、不确定和不完全数据的有效数学工具，采用目标集合的上近似和下近似表达模糊信息。粗糙数采用区间数的形式来表达信息的不确定性，利用所需要处理的数据确定区间的下限和上限。粗糙数的确定过程不需要额外的先验知识来分析数据，保持了信息的客观性，且与其他不确定性问题的理论有很强的互补性[18]。

假设U 是包含主轴轴承某一失效模式所有专家评价信息的论域，专家给出的评价信息R={C1,C2,···,CL}，且C1＜C2＜···＜CL。则对于Ck∈R(1 ≤k ≤L)， Ck的下近似Apr(Ck)和上近似Ck)分别定义为：

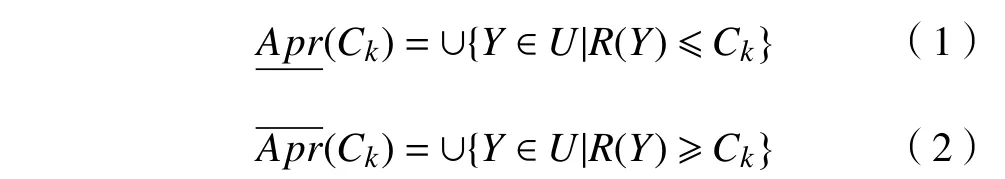
评价值Ck由其相应的下限Ck)和上限Ck)组成的粗糙数表示为：

则Ck的不确定性可以表示为

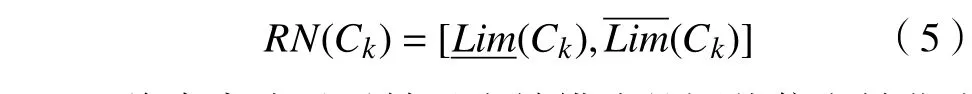
将专家成员对轴承失效模式的评价信息转化为粗糙集形式，则专家成员对主轴轴承失效模式的风险评估矩阵Vk=(vkij)可以转换为粗糙集评估矩阵。

式中： RN(vkij)为vkij的粗糙集区间；分别为 vkij的下限和上限。

1.3 粗糙云评估矩阵模型

云模型是处理定性概念与定量描述的不确定转换模型，是一种新的不确定性认知方法。在概率论和模糊集理论的基础上，统一刻画了语言信息的模糊性和随机性及二者之间的关系，能够很好的描述人类思维中概念的不确定性[19]。

云由期望Ex、熵En、超熵He这3个数值参数来描述，其中期望Ex 是论域的中心值，熵En是描述问题的随机性和模糊性特点，熵越大，随机性和模糊性越大。超熵He 是熵的熵，用来表示熵的不确定性，反应云滴的离散程度。通常云可以表示为y =（Ex,En,He），其中期望Ex 也可用区间Ex]来表示，此时云模型将转化为区间云的形式En，He）。

1）如果Sab＞ 0，则y1＞ y2；

2）如果Sab= 0、En1＜ En2，则y1＞ y2；

3）如果Sab=0、En1= En2、He1＜ He2，则y1＞ y2；

4）如果Sab= 0、En1= En2、He1= He2，则y1= y2。

且有如下运算规则：将专家评价信息的粗糙集区间作为区间云的期望]，转换为相应的区间云形式，则粗糙集评估矩阵可转换为粗糙云评估矩阵。

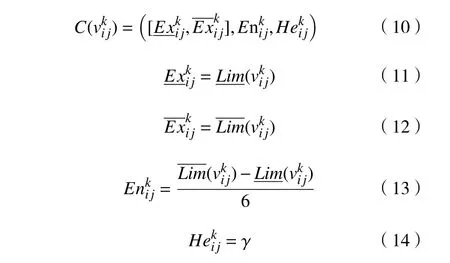
式中：C(vkij) 为 vkij的粗糙云评价值；[], Enkij， Hekij为区间云模型的3个特征；γ 为常数，根据不确定程度确定。

2 轴承失效模式重要度评估

为了解决传统FMEA 模型所存在的问题，本文提出了一种粗糙云模型与PROMETHEE 的改进FMEA 方法。该方法主要包括3 个部分：1）粗糙云模型的FMEA 建模；2）专家成员与风险元素综合权重的确定；3）粗糙云与PROMETHEE 的航发主轴轴承失效模式风险排序。改进FMEA方法的框架流程图如图1所示。

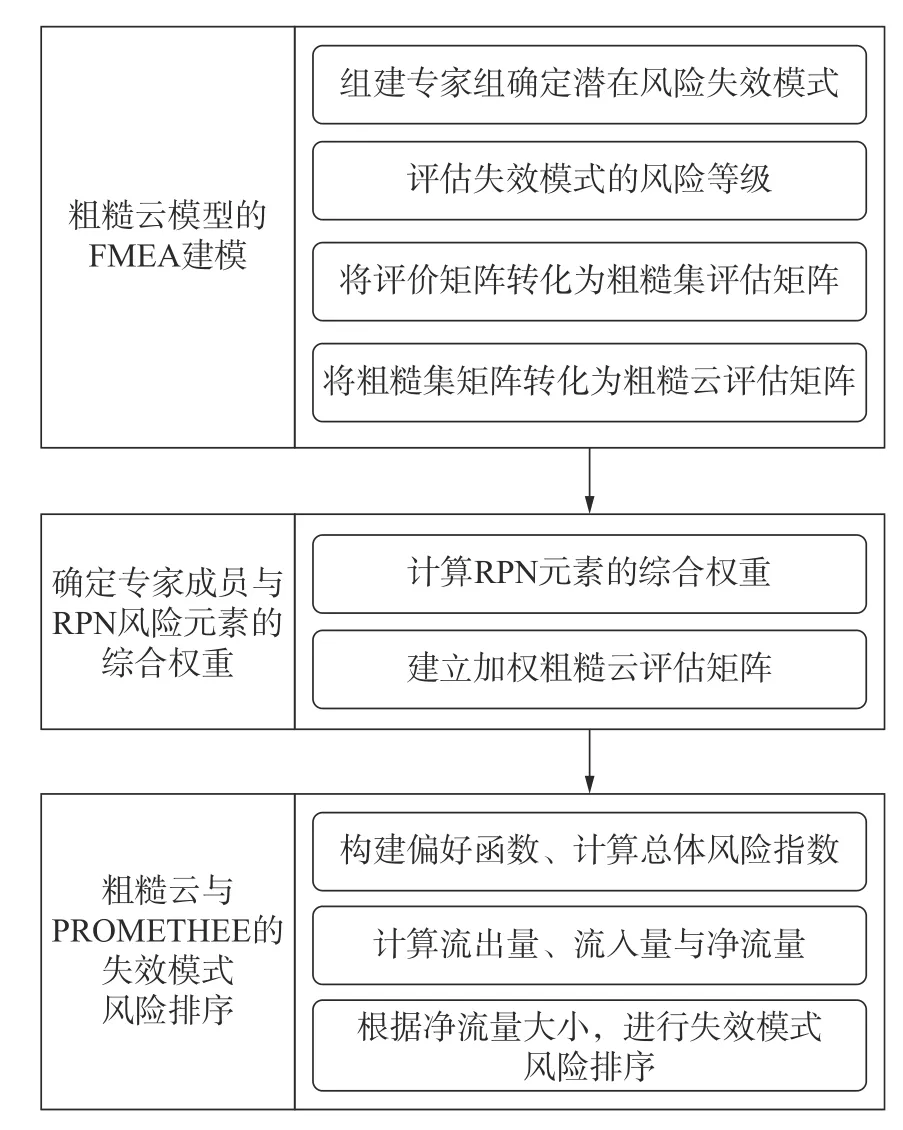
图1 改进FMEA 方法的框架流程图

2.1 专家成员与风险元素的综合权重

2.1.1 计算RPN 元素的综合权重

采用方差来表示RPN 元素的客观权重[15]，方差越大，包含的信息越多，相应的RPN 元素越重要。RPN 元素综合权重的确定方法为：

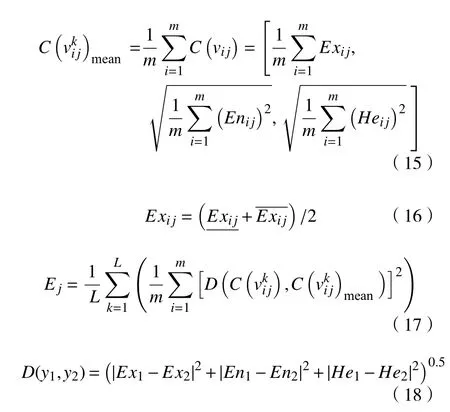
式中：C(vkij)mean为C(vkij)的平均值； Ej为故障模式的评估值在第j 个RPN 元素下的方差。

RPN 元素的客观权重定义为

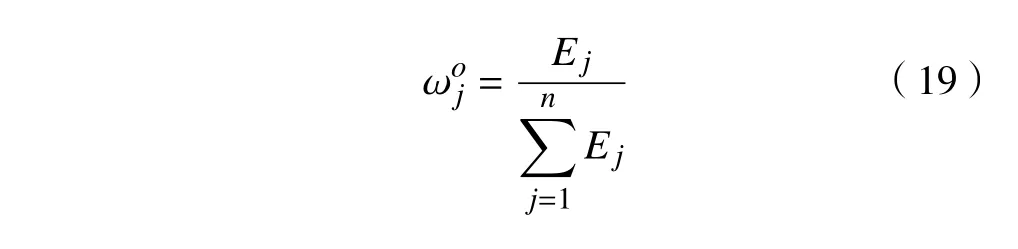
则RPN 元素的综合权重定义为

式中： ωj为RPN 的综合权重； ωsj为RPN 元素的主观权重，可由最小二乘法、德尔菲法等确定； θ为客观权重的相对重要程度，一般取0.5。

2.1.2 建立加权粗糙云矩阵

计算加权平均算子（CWAO），将所有专家成员的评价矩阵集成为加权粗糙云矩阵。集成粗糙云C(vij)计算式为

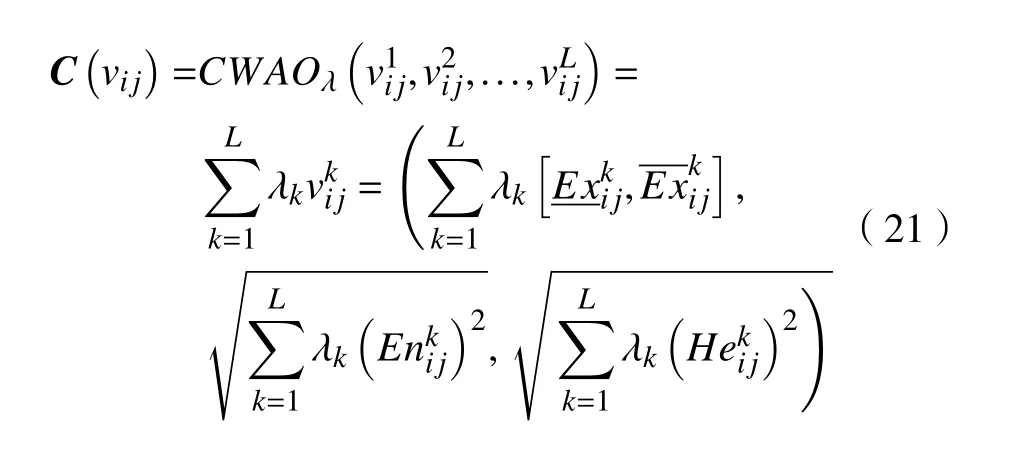
式中 λk为专家成员的权重。

则加权粗糙云矩阵C (vij)m×n为

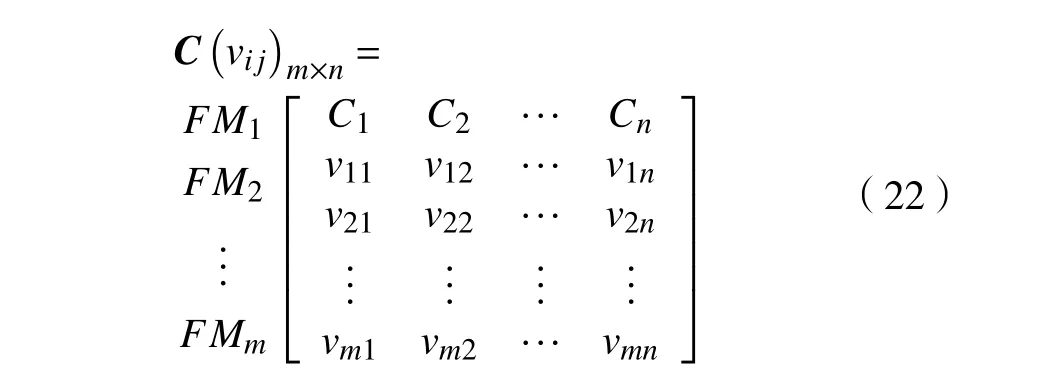
2.2 粗糙云与PROMETHEE的失效模式风险排序

PROMETHEE是一种基于优先关系的多准则决策方法，通过构建偏好函数计算每种轴承失效模式的正流量、负流量和净流量，最后以净流量为标准对航发主轴轴承失效模式进行风险排序，净流量越大，风险越大。粗糙云模型与PROMETHEE的失效模式风险排序方法步骤如下。

2.2.1 构建总体风险指数

在传统的PROMETHEE方法中有6种典型的偏好函数，但都需要事先确定无差异阈值、绝对偏好阈值等参数。在实际应用过程中，决策者很难确定合适的偏好函数及相应的参数，且具有较大的主观性，这将直接影响到最终的排序结果。为避免这一情况，采用一种简化的偏好函数[17]：

式中： d(vpj,vqj)为加权粗糙云矩阵中云 vpj和vqj的距离，j=1,2,···,n，其中发生频率与严重程度的评价值越高，失效模式的潜在风险程度越高，而可探测程度的评价值越小，其风险程度越高。因此在风险元素可探测程度下比较两失效模式云模型的大小时，计算所得的Sab取其相反数； Rj(FMp,FMq)为第j 个RPN 元素下FMp比FMq具有更高风险的程度。

计算总体风险指数为

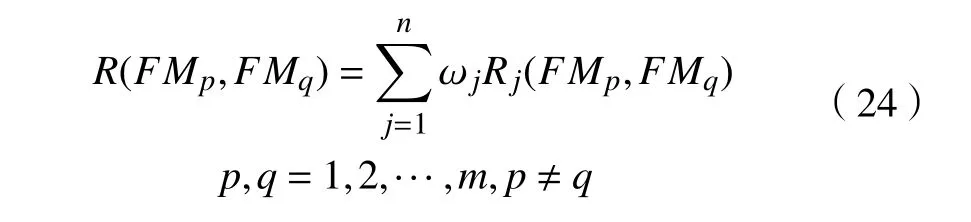
2.2.2 失效模式的风险排序

流出量表示FMp高于FMq的风险指数为

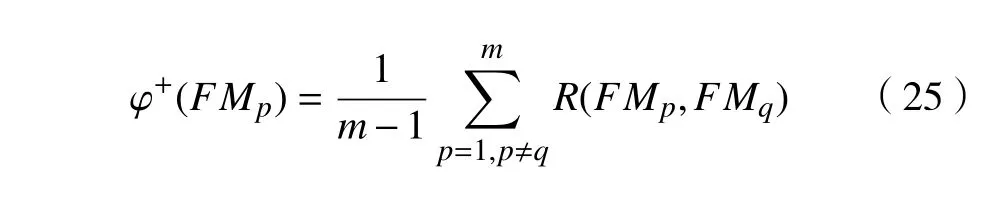
流入量表示FMp低于FMq的风险指数为

计算轴承失效模式的净流量为

式中： φ(FMp)越大，对应的失效模式越重要，以净流量为标准将主轴轴承失效模式降序排列。

3 实例计算与分析

3.1 航发主轴轴承失效模式重要度评估

以WP6与WP7发动机主轴轴承为主要研究对象，综合其运行工况与工作特点，确定其6种主要潜在失效模式（摩擦磨损、锈蚀锈斑、打滑蹭伤、划伤压坑、疲劳剥落、保持架损坏）[20-24]，分析其形成原因与预防措施，如表2所示。结合相关统计数据[22]，根据表1从发生频率（O）、严重程度（S）、可检测程度（D）方面对失效模式进行综合风险评估。航发主轴轴承失效模式的风险评估矩阵如表3所示。

表2 航发主轴轴承主要潜在失效模式

表3 航发主轴轴承失效模式的风险评估矩阵

根据式（1）～ 式（6）得到的风险评估矩阵转换为粗糙集评估矩阵，TM1的粗糙集评估矩阵见表4。

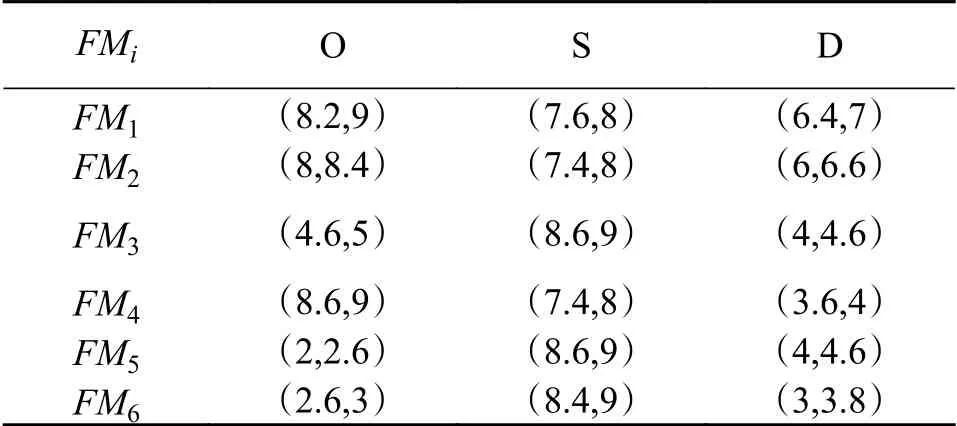
表4 TM 1的粗糙集评估矩阵

根据式（10）～式（14）将粗糙集评估矩阵转化为粗糙云评估矩阵，TM1的粗糙云评估矩阵如表5 所示。

表5 TM 1的粗糙云评估矩阵

因专家成员在专业知识、资历上的不同，由专家小组确定各专家成员的权重，根据式（15）～式（20）计算RPN 元素的客观、综合权重，结果如表6所示。根据式（7）、式（8）及式（21）计算加权粗糙云评估矩阵，结果如表7所示。

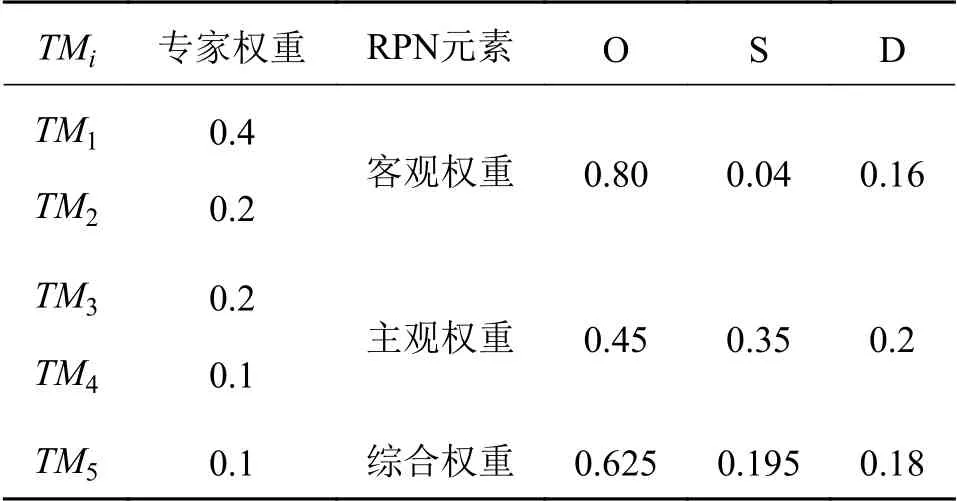
表6 专家成员与风险元的权重

表7 加权粗糙云评估矩阵

根据偏好函数以及RPN 元素综合权重计算轴承失效模式的总体风险指数，如表8所示。计算失效模式的流出量、流入量和净流量，并以净流量为标准对主轴轴承的主要潜在失效模式进行风险排序，航发主轴轴承失效模式风险排序的重要度评估如表9所示。

表8 总体风险指数

表9 航发主轴轴承失效模式风险排序

3.2 评估结果分析

同传统FMEA方法和粗糙云与TOPSIS的改进FMEA 方法进行对比分析，由这些方法得到的航发主轴轴承失效模式风险排序如表10所示。

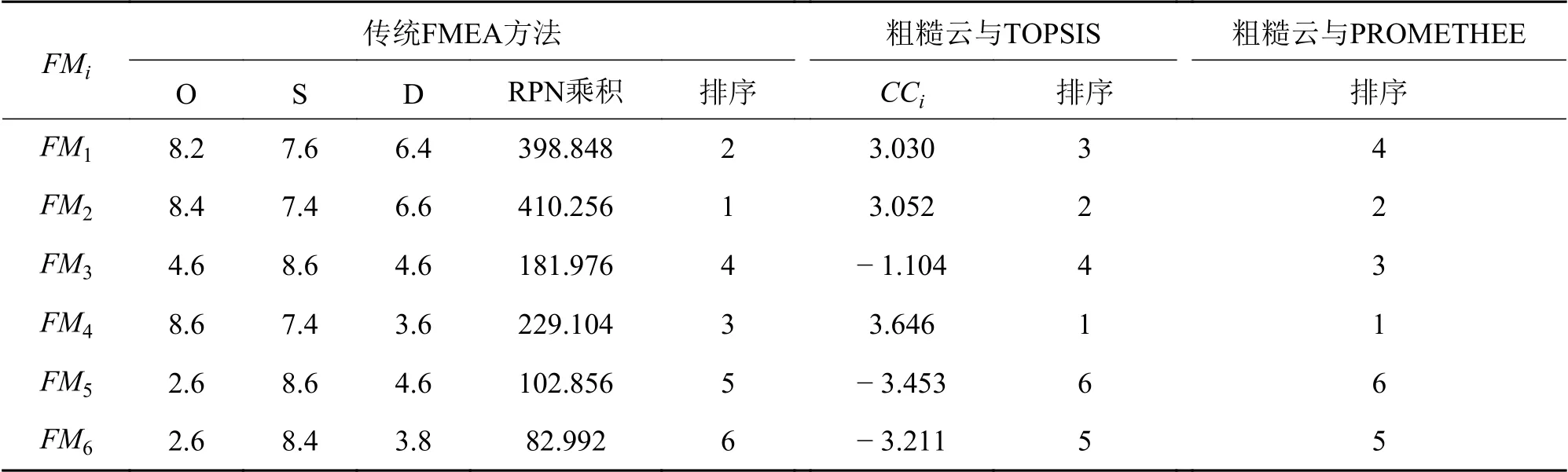
表10 3种不同FMEA 方法的风险排序结果

由表10 可知，虽然本文方法和粗糙云与TOPSIS改进FMEA 方法的故障模式排序结果不完全相同，但最高和最低的失效模式都被确定为FM4和FM5，表明本文提出的改进FMEA 方法可以有效识别航发主轴轴承的关键失效模式，航发主轴轴承的关键失效模式为划伤压痕、锈蚀锈斑，其次为打滑蹭伤、摩擦磨损、保持架损坏、疲劳剥落。

另外，本文方法的故障模式排序结果与传统的FMEA 方法差距较为明显，对比粗糙云与TOPSIS改进FMEA方法的排序结果，FM1和FM3的顺序互换。其可能的原因如下：

1）对比传统FMEA 方法采用清晰的数字进行评估，且各风险元素的采用相同的风险权重，本文方法采用粗糙云的形式描述专家的评价信息中的主观性、模糊性和随机性，且综合考虑专家、风险元素的权重，更接近实际情况；

2）粗糙云与TOPSIS改进FMEA 方法中云模型的期望Ex采用粗糙集上近似与下近似均值的形式表示，但不同粗糙集可能得到相近甚至相同的均值结果，本文采用区间云的形式，保留了粗糙集的全部信息。同时TOPSIS方法具有决策补偿性，单一指标的高评价值对最终结果有较大的影响，而PROMETHEE方法通过两两对比的方式进行评估，结果更加准确。

4 结论

1）将粗糙集与区间云结合，充分保留了粗糙集的信息，更好的反映了专家评价信息中的主观性与不确定性。

2）将偏好顺序结构评估法（PROMETHEE）与FMEA 方法相结合，通过两两对比的方式对航发主轴轴承各失效模式进行评估，并与传统FMEA 方法、粗糙云与TOPSIS改进FMEA 方法对比，具有良好的有效性与适用性。