纤维增强FGM 梁的自由振动和临界屈曲载荷分析

滕兆春，王伟斌，马铃权

（兰州理工大学 理学院，兰州 730050）

功 能 梯 度 材 料 （Functionally graded material，FGM） 是一种特殊的非均匀复合材料，它是通过特定的材料制备工艺将不同性能的两种或两种以上材料按一定的设计规律组合起来，使材料组分按梯度连续变化的先进复合材料，具有减缓热应力及应力集中等优异的力学性能[1]。FGM 最初设计被用做航天飞机外壳耐热问题，后来被广泛应用于航空航天，能源，交通，建筑，机械，船舶，土木，生物等领域[2]。尤其是航天航空飞行器的设计和发展过程中，其安全性能是设计的一个重要因素。FGM 这种非均匀复合材料结构的力学行为研究要比均匀材料结构相对要复杂得多，目前关于FGM 结构的力学行为研究，也已有较多的研究成果，具体可参考Reddy、Wattanasakulpong 和Ebrahimi 等学者[3-5]的系列研究工作。最近，Ghazaryan 等[6]研究了不同边界条件下非均匀截面FGM 梁的自由振动，计算了不同变截面FGM 梁的固有频率响应。Abdolhossein 等[7]研究了弹性地基上的FGM 部分充液圆柱壳在热环境下的力学性能，得到了幂律指数、液体深度和温度对壳的无量纲固有频率的影响。滕兆春等[8]基于Timoshenko 梁理论，采用微分变换法（Differential transform method，DTM） 研究了弹性地基上转动FGM梁的自由振动问题，计算并分析了不同边界条件下转速、弹性地基模量和梯度指数与横向自由振动无量纲固有频率之间的关系。林鹏程等[9]应用微分求积法（DQM）研究了热冲击下轴向运动FGM 梁的自由振动，考虑了不同热冲击载荷、梯度指数和轴向运动无量纲速度对FGM 梁自振频率的影响。Gupta等[10]应用非多项式高阶剪切和法向变形理论，研究了不同边界条件、几何条件、微观力学模型和地基参数下FGM 板的弯曲和振动响应。蒋伟男等[11]基于3 阶剪切理论提出考虑横向拉伸影响的位移场，研究了具有简支和固支边界条件的FGM 夹层矩形板的自由振动问题。李万春等[12]用传递矩阵法（TMM）对变曲率FGM 拱的面内自由振动固有频率特性进行了分析。

在基体中加入颗粒、短纤维或长纤维等而形成的增强复合材料因具有更好的强度和刚度一直受到人们的关注并在工程实际中大量使用，也已有一些学者开始对增强FGM 结构进行了研究工作。贺丹等[13]基于一种新的各向异性修正偶应力理论，研究了碳纳米管增强型复合材料功能梯度板的自由振动模型与尺度效应，讨论了板的几何尺寸，碳纳米管体分比含量和分布方式对板的自由振动频率的影响。李晓倩等[14]基于修正的Halpin-Tsai 模型，估算了石墨烯纳米材料复合材料的杨氏模量和剪切杨氏模量，进而研究了温度场下石墨烯增强功能梯度梁的主共振行为分析。Nejati 等[15]在稳态热环境下纤维增强的功能梯度板的自由振动。Shen 等[16]研究了热环境下弹性地基碳纳米管复合材料梁的非线性分析。Yas 等[17]考虑了4 种不同的碳纳米管分布，研究了弹性地基上碳纳米管增强Timoshenko 复合材料梁的自由振动与屈曲。Thomas 等[18]等基于Mori-Tanaka 模型研究了任意取向碳纳米管增强功能梯度纳米复合梁的有限元建模及自由振动，通过引入不同厚度方向的SWCNTs 分布来改善均匀功能梯度纳米复合材料梁的固有频率和动力学响应。

作为一种优异的热障材料，FGM 一般是由陶瓷和金属材料复合而成。为提高FGM 结构的断裂韧性，可在FGM 基体中植入均匀或非均匀分布的连续纤维增强而形成功能梯度复合材料[19]。目前，关于纤维增强复合材料结构中基体由两相材料构成且为功能梯度材料的力学行为研究在国内外鲜见有文献报道。本文基于经典梁（CBT）理论，考虑将FGM梁作为基体进行均匀分布的纤维增强，由指数模型和混合率公式计算纤维增强FGM 梁的等效物性参数，使用Hamilton 原理导出轴向力作用下纤维增强FGM 梁横向自由振动和临界屈曲载荷的控制微分方程，再利用微分变换法（DTM）对梁的控制微分方程和边界条件进行变换，得到求解纤维增强FGM梁无量纲固有频率和临界屈曲载荷的代数特征方程。退化为无纤维的各向同性梁和FGM 梁，并与已有文献结果进行对比，验证本文方法的有效性。考虑并分析了不同边界条件下刚度比、无量纲压载荷、纤维体积分数、对纤维增强FGM 梁横向自由振动固有频率的影响以及各参数对临界屈曲载荷的影响。

1 数学模型及材料物性参数的描述

考虑一纤维增强FGM 梁，建立如图1 所示的笛卡尔三维坐标系 xy z。梁长为L，宽为b，高为h，其中弹性模量为E，密度为ρ，梁两端受初始轴向压载荷N。

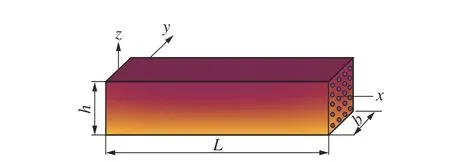
图 1 纤维增强FGM 梁的几何描述

对于纤维增强FGM 的物性参数可由混合率公式[20]表示为

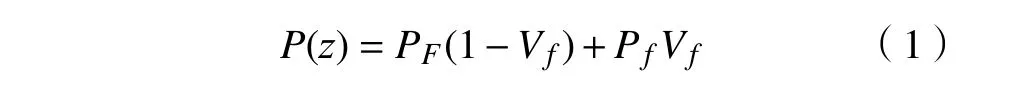
基体FGM 的物性参数则由指数模型给出[21]，即

式中：P 为弹性模量和密度；V 为体积分数；下标F 表示FGM 基体，c 表示陶瓷；m 表示金属；f 表示纤维，其中

2 控制微分方程及参数的无量纲化

对纤维增强FGM 梁，采用Hamilton 原理，则

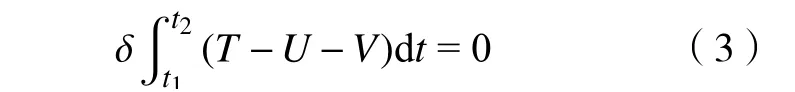
式中： T、 U和 V分别为系统的动能、应变能和外力势能； δ为变分符号； t1和 t2为时间。在经典梁理论（CBT）下，纤维增强FGM 梁中T、U 和V 的表达式分别为：

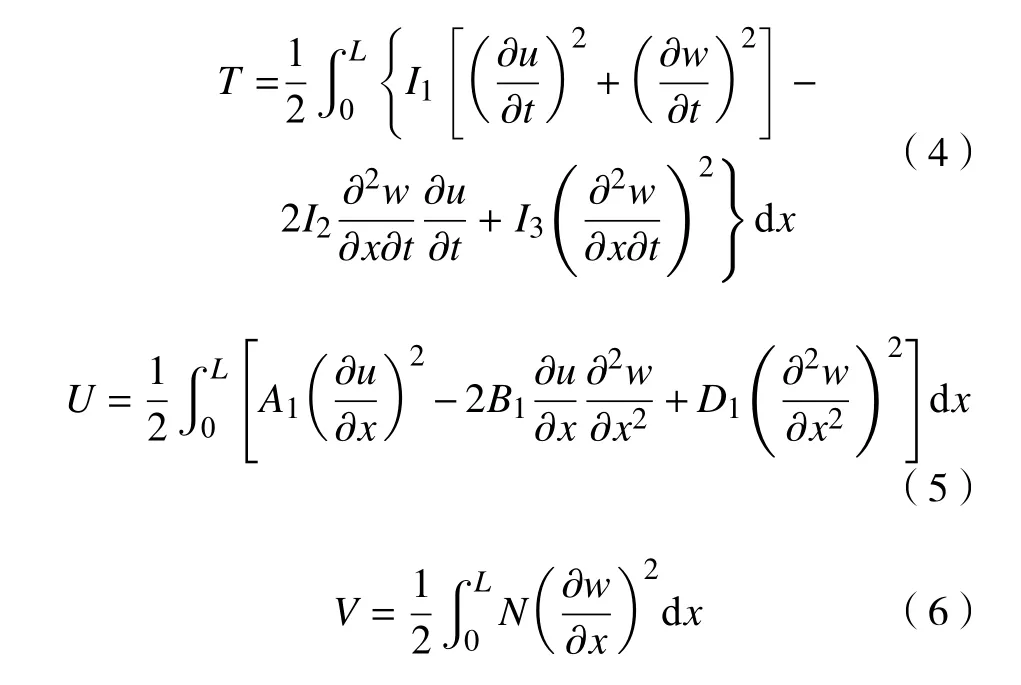
式中：t为时间； u和 w分别为纤维增强FGM 梁上一点在 x方向和 z方向的位移。其它系数A1、B1、D1、I1、I2和I3分别为：

式中： A1为拉伸刚度系数； B1为拉-弯耦合刚度系数；D1为弯曲刚度系数；I=bh3/12为截面惯性矩，A=bh为横截面面积。其中6 个无量纲系数表示为：

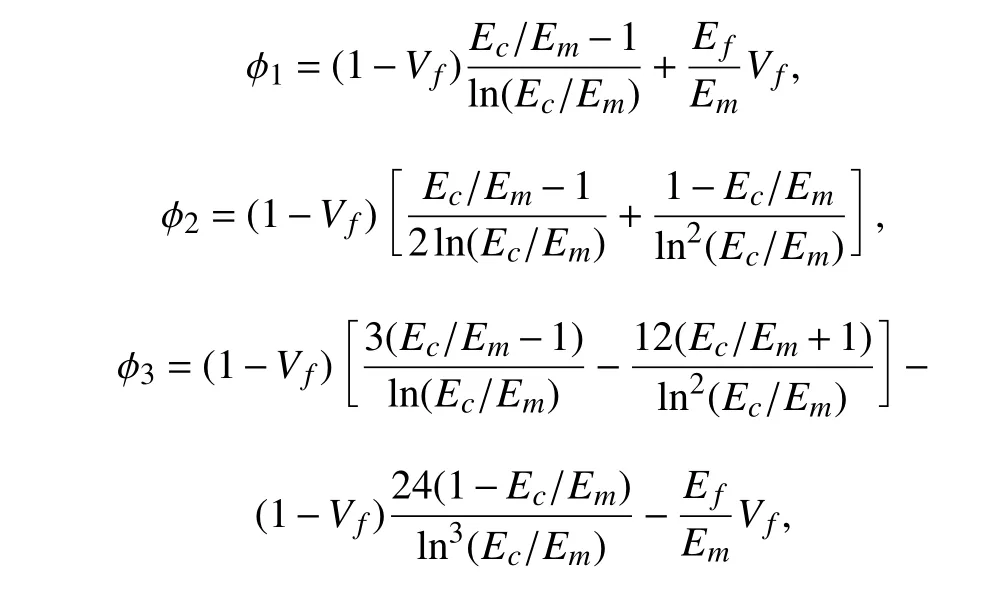
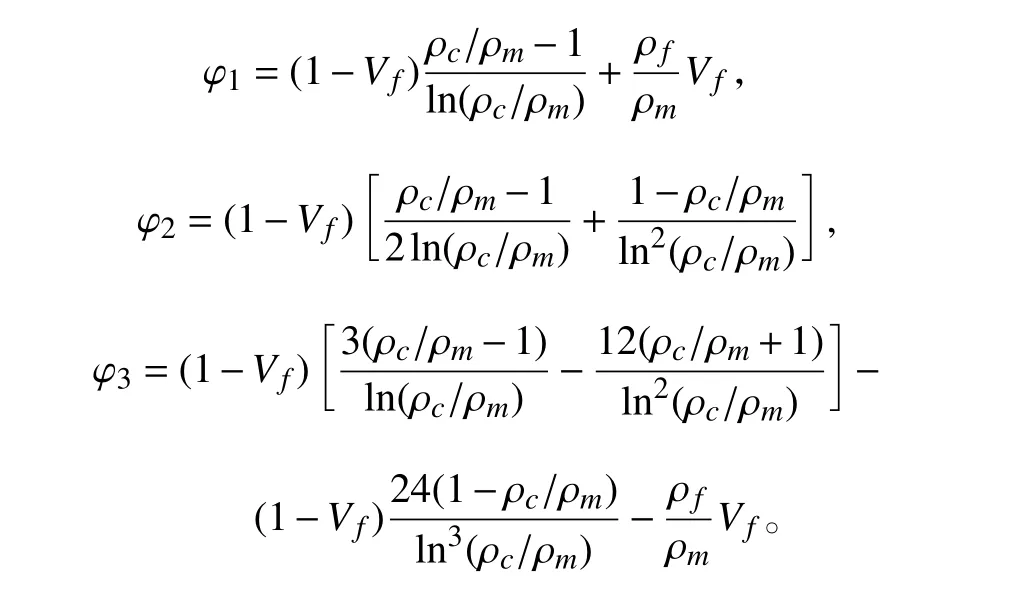
将式（4）～式（6）代入式（3），应用变分原理，并忽略因横向弯曲产生的纵向和转动惯性力。可以得到纤维增强FGM 梁关于u 与w 的两个运动控制微分方程为：

联立式（7）和式（8）消去轴向位移，可以得到

对纤维增强FGM 梁的简谐运动，可令

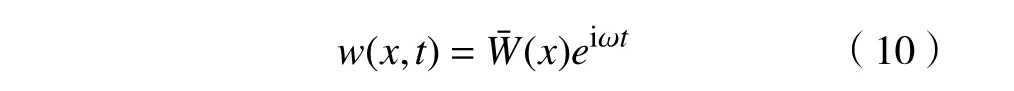
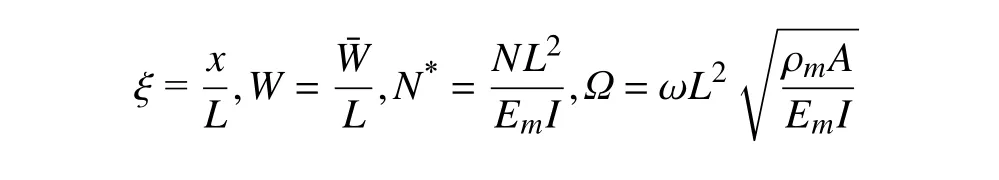
式中： Ω为无量纲固有频率； N*为无量纲压载荷。由此可以得到纤维增强FGM 梁关于无量纲固频率Ω的特征方程为

另由弹性稳定性理论可知，当屈曲载荷使得系统发生屈曲失稳时，其固有频率将变为零。故式（11）中Ω=0时，其也可以表示纤维增强FGM 梁屈曲时关于无量纲临界屈曲载荷 Ncr的特征方程。

对于纤维增强FGM 梁在ξ=0和ξ=1处的边界条件如下：

固定（C）

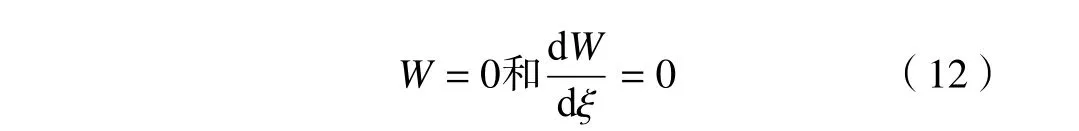
简支（S）

3 控制微分方程及边界条件的DTM变换

微分变换法（DTM）是一种将微分方程转化为代数方程有效的半解析法，它是基于Taylor 级数展开进而求解微分方程，非常适合计算机编程计算，一些研究结果[2,6,8]都很好地验证了该方法在求解微分方程特征值问题时的实用性和有效性。运用 DTM对纤维增强FGM 梁自由振动和临界屈曲载荷的控制方程进行求解时，首先需要将其无量纲控制微分方程和边界条件经 DTM 变换为相应的代数特征方程，其具体变换过程可参考文献[2]。这里用F 表示经DTM 变换后的函数，则纤维增强FGM 梁自由振动和临界屈曲载荷的控制微分方程（11）经DTM 变换后为：

对边界条件也进行DTM 变换：

在ξ=0处：

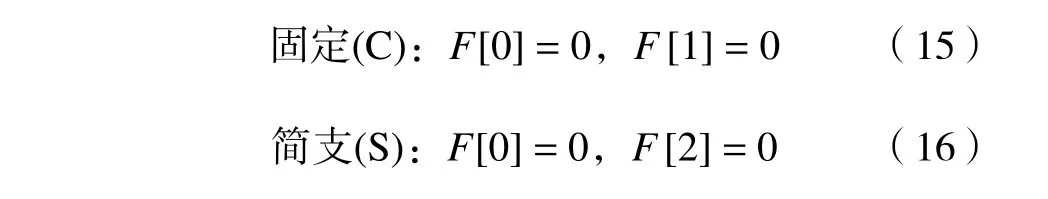
在ξ=1处：

固定（C）:

简支（S）:

4 计算结果及分析

边界条件式（15）～式（18）和DTM 变换后的纤维增强FGM 梁自由振动和临界屈曲载荷的代数特征方程（14）进行迭代求解即可得到不同边界条件下纤维增强FGM 梁横向自由振动的无量纲固有频率和无量纲临界屈曲载荷。通过MATLAB 编程进行计算过程如下：

算例 碳纤维、陶瓷和金属的物性参数[20-21]：Ef=400 GPa，ρf=1 800 kg/m3，Ec=380 GPa，ρc=3 800 kg/m3， Em=70 GPa，ρm=2 780 kg/m3。

表1 给出了 C-C、C-S 和S-S 边界条件下，控制微分方程退化为各向同性梁，即刚度比Pc/Pm=1情况下，计算了前5 阶无量纲固有频率并和文献[21]的精确解做了比较。由表1 可知，结果完全吻合，验证了计算模型的准确性及求解方法的有效性。

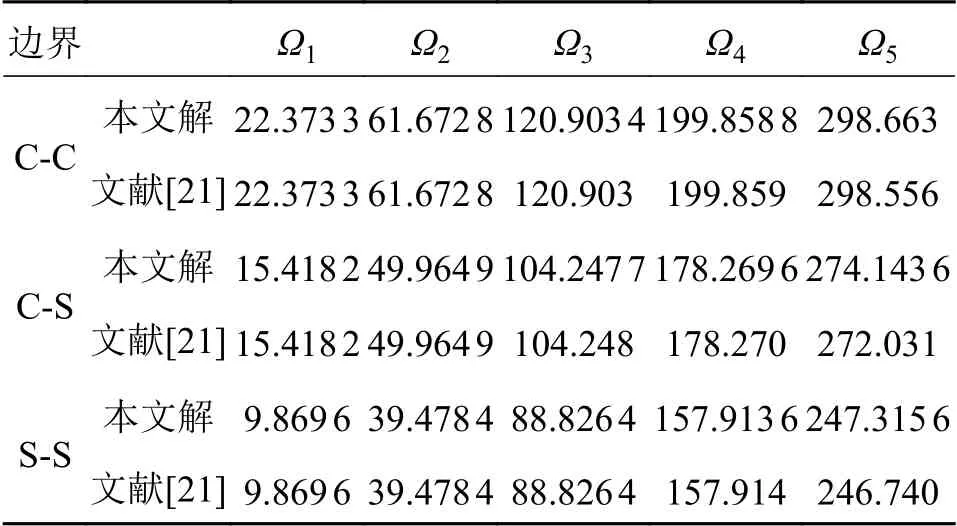
表1 不同边界条件各向同性材料梁的无量纲固有频率

表2 给出了 C-C、C-S 和S-S 边界条件下，在不同刚度比下，控制微分方程退化为FGM 梁，应用DTM计算了其前五阶无量纲固有频率，并和文献[21]的精确解结果做了比较。由表2 可知，结果也完全吻合，可以看出DTM 计算精度满足要求，说明了DTM对于研究本问题的适用性。

表2 不同边界条件下FGM 梁无量纲固有频率

图2 分别反映了当Vf=0．1， N*=0时，在C-C、C-S 和S-S 这3 种不同边界下，刚度比Pc/Pm与前5 阶无量纲固有频率Ω 的关系曲线。结果显示：由于刚度比 Pc/Pm的取值是从1 到200 之间，在边界条件一定情况下，随着刚度比Pc/Pm的增大，纤维增强FGM 梁的前5 阶无量纲固有频率整体在减小后基本趋于不变，当刚度比Pc/Pm在小值范围取值时，无量纲固有频率减小趋势很剧烈，当 Pc/Pm在较大值范围取值时，无量纲固有频率变化趋于平缓，此时刚度比的大小反映功能梯度的特性，并合理的解释了FGM 中陶瓷材料向金属材料过渡的特性。并且，当Pc/Pm的值一定时，边界约束越强，无量纲固有频率越大，即：C-C 边界无量纲固有频率＞C-S 边界无量纲固有频率＞S-S 边界无量纲固有频率。

图 2 不同边界条件下刚度比Pc/Pm对纤维增强FGM 梁前5 阶固有频率的影响

图3 刻画了当 Pc/Pm=2 ， N*=0时，在C-C、 C-S和S-S 这3 种不同边界条件下，纤维的体积分数Vf与无量纲固有频率 Ω的关系曲线。结果表明：在CC、C-S 和S-S 边界条件下，随着纤维体积分数Vf的增大，纤维增强FGM 梁的前3 阶无量纲固有频率Ω在线性增大。还能看出，前3 阶无量纲固有频率随碳纤维体积分数的增大变化较小，但可以说明纤维体积含量对功能梯度材料梁的无量纲固有频率是有影响的。另外，当Vf的值一定时，同样边界约束条件越强，无量纲固有频率越大。即：C-C 边界无量纲固有频率＞C-S 边界无量纲固有频率＞S-S 边界无量纲固有频率。

图 3 不同边界条件下纤维体积分数Vf 对纤维增强FGM 梁前3 阶无量纲固有频率的影响

图4 为在C-C、C-S 和S-S 这3 种不同边界条件下取无量纲固有频率 Ω为零时，对应的最小载荷值即为临界屈曲载荷。取 Vf=0．1，分析了不同刚度比Pc/Pm对无量纲临界屈曲载荷 Ncr的影响。随着刚度比 Pc/Pm的增大无量纲临界载荷增大，并且边界条件约束越强，无量纲临界屈曲载荷越大，即：C-C边界无量纲临界载荷＞C-S边界无量纲临界载荷＞S-S边界无量纲临界载荷。

图4不同边界下刚度比P c/Pm对无量纲临界屈曲载荷的影响

图5 为在C-C、C-S和S-S这3种不同边界下，取Pc/Pm=2，给出了增强纤维的体积分数Vf和无量纲临界屈曲载荷 Ncr的关系曲线。由图5可见，随着纤维体积分数Vf的增大无量纲临界载荷在线性增大，说明纤维的加入对临界屈曲载荷有明显的影响，并且边界条件约束越强，无量纲临界屈曲载荷越大，即：C-C 边界无量纲临界载荷＞C-S边界无量纲临界载荷＞S-S边界无量纲临界载荷。

图5不同边界条件下纤维体积分数和无量纲临界屈曲载荷的关系曲线

图6 为在C-C、C-S和S-S这3种不同边界下，取Pc/Pm=2，在Vf=0 和Vf=0．2时，研究了无量纲压载荷对一阶无量纲固有频率的影响，分别得到了有、无纤维增强时对FGM梁的无量纲固有频率Ω1（即基频）的影响曲线。结果显示，无量纲固有频率随无量纲压载荷 N*的增大而减小，且边界条件约束越强，无量纲固有频率越大，即：C-C 边界无量纲临界载荷＞C-S边界无量纲临界载荷＞S-S边界无量纲临界载荷。同时，当无量纲载荷一定时，在同种边界下，有纤维增强的无量纲固有频率大于无纤维增强的无量纲固有频率，说明纤维的加入FGM的振动特性有明显的影响。

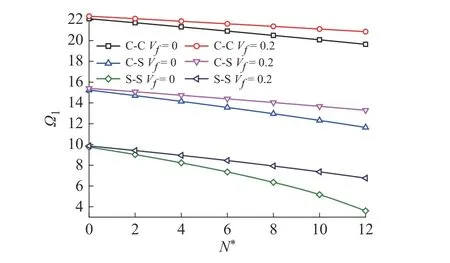
图6 不同边界条件和不同纤维体积分数下无量纲压载荷对一阶无量纲固有频率的影响

5 结论

1）在纤维体积分数Vf和无量纲载荷 N*一定时，纤维增强FGM梁在C-C、C-S和S-S这3种不同边界条件下，随着刚度比 Pc/Pm的增大，无量纲固有频率 Ω减小后趋于不变，合理的解释了FGM中陶瓷材料向金属材料过过渡的特性，而无量纲临界载荷Ncr增大，同时，边界约束越强，无量纲固有频率和无量纲临界载荷越大。

2）在刚度比 Pc/Pm和无量纲载荷 N*一定时，在C-C、C-S和S-S这3种边界下，纤维增强FGM梁都有共性，无量纲固有频率 Ω和无量纲临界载荷都是随着Vf的增大而线性增大，且随无量纲固有频率变化较为缓慢，同时，边界约束越强，无量纲固有频率和无量纲临界载荷越大。

3）在刚度比Pc/Pm和纤维体积分数Vf一定时，在C-C、C-S和S-S这3种边界下，1阶无量纲固有频率Ω1都是随着无量纲载荷增大而减小，而边界约束越强，无量纲固有频率越大，同时有纤维增强比无纤维的无量纲固有频率要大。