振动图像结合CNN的轴承振动信号分析方法研究

2022-02-13郝勇刘尚宗吴文辉

机械科学与技术 2022年12期

郝勇，刘尚宗，吴文辉

（1.华东交通大学机电与车辆工程学院，南昌330013；2.青岛四方庞巴迪铁路运输设备有限公司，山东青岛266111）

振动信号分析广泛应用于机械设备的故障诊断和健康状态测试与维护。轴承是机械设备中一种重要零部件，它的主要功用是支撑机械旋转体，降低其运动过程中的摩擦因数，并保证其回转精度，其质量优劣直接影响机械系统的寿命、安全性和稳定性[1]，在旋转机械中有70%的故障是由滚动轴承引起的。轴承振动信号具有非线性、非平稳和缺陷特征微弱的特点[2-3]，因此，从振动信号中直接提取轴承的故障特征较困难且不准确，需要探索一种适用于强背景干扰下的信号特征提取和分析方法实现轴承品质的评估。

振动信号结合机器学习方法常用于轴承的故障诊断和质量品质评估模型的建立[4]。然而，传统的机器学习算法如支持向量机（Support vector machine,SVM）对于大数据训练样本会耗费大量机器内存与运算时间，对于非线性问题还需要选择最优核函数[5]；决策树（Decision tree）不支持在线学习，且会忽略数据集属性间的相关性，模型容易过拟合；逻辑回归（Logistic regression）只能处理两分类问题，对多类特征不能很好处理，容易欠拟合。因此，传统的机器学习算法虽然结构简单，但是在复杂非线性关系的分类问题中其分析能力受到极大限制。

近年来，深度学习作为自动提取特征的典型方法应用于智能故障诊断。Kong 等[6]提出一种新颖的正则化策略，在堆栈自编码模型训练中引入内积，，构造出基于内部产品的堆栈式自编码模型，用以改善工业过程的深层特征。叶状等[7]利用经验模态分解方法得到多通道一维信号，构建多通道一维卷积神经网络（Multi-channel one-dimensional convolutional neural network,MC-1DCNN）模型进行特征提取。在MC-1DCNN的全连接层后接堆叠降噪自编码器层，进一步进行维度缩减和特征提取并实现特征分类。李益兵等[8]利用粒子群优化（Particle swarm optimization,PSO）算法优选深度置信网络（Deep belief nets,DBN）网络结构，随后运用具有最优结构的DBN 模型直接提取低维故障特征，并将故障特征输入轴承故障识别模型进行故障判断。Wang 等[9]提出了一种基于强化学习的神经网络体系结构自动搜索方法，用于滚动轴承的故障诊断，该方法以递归神经网络（Recursive neural network,RNN）为控制器生成一系列动作，每个动作指定一种设计选择，以构造用于故障诊断的子模型。CNN 是一种有监督深度学习模型，具有局部区域感知、权重共享和空间采样3个关键的架构思想，适用于处理高维数据[10-11]，并且是含有多层处理单元的特征学习方法，可以将输入层的数据逐层转换成更易于识别的特征[12]。

论文针对强背景干扰下振动信号的特征提取和建模分析问题，以滚动轴承的故障诊断和质量品质评估振动信号作为实验数据集，提出了一种基于振动图像（Vibration image,VI）结合CNN的轴承故障诊断与质量评估方法：将振动信号转为二维振动图像，结合CNN方法提取图像多维特征信息并进行建模分析，以期实现噪声影响下振动信号的有效特征提取和精确稳定的模型构建。

1 算法与理论

1.1 振动图像构建方法

在轴承故障诊断和质量品质评估过程中，采集的振动信号包含了丰富的质量品质信息和设备运行产生的冲击等干扰响应信息，由于时域信号不相邻样本点间关系获取比较困难，若将其转换为振动图像，获取给定图像元素与其相邻图像元素间的关系相对容易。因此，为了有效提取振动信号样本点间关系信息，将振动信号转换为振动图像，样本幅值归一化到[-1,1]，然后将归一化的样本幅值转换为图像像素值[13-14]。图1所示为振动信号转换为振动图像的构建过程示意图。

图1 振动图像构建过程示意图

样本幅值与对应图像像素值的表达式为

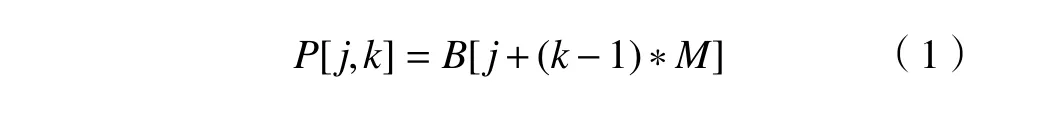
式中：M 为图像尺寸长度；N 为图像尺寸宽度；j=1∶M;k =1∶N; P[ j,k]为M × N 大小振动图像对应像素的强度；B[·]是振动信号中样本点转化的幅值。振动图像中像素的个数等于振动信号中样本点的个数。

1.2 振动信号预处理及建模分析方法

1.2.1 振动信号时域特征分析

在振动信号分析过程中，实验采集的滚动轴承振动信号包含了轴承工作的全部信息，具有较强的时域信息，因此对信号进行时域特征提取是一种最直接、最有效的特征提取方法。振动信号时域特征（Vibration signal time domain feature,VSTF）提取获取信号时域特征参数。

时域特征参数可分为有量纲和无量纲。本文有量纲特征统计参数为均值、均方根值、方根幅值、绝对平均值、偏斜度、峭度、方差、最大值、最小值、峰峰值；波形指标、峰值指标、脉冲指标、裕度指标、偏斜度指标、峭度指标等特征为无量纲统计参数。

1.2.2 梯度方向直方图算子

梯度方向直方图（Histogram of oriented gridients，HOG）源于SIFT算法，是一种图像局部特征描述符，通过对图像中某一矩形区域中像素点梯度幅值和方向综合信息的统计来获取图像特征。

1）每个像素点梯度以及估算梯度的幅值G(x, y)和方向α(x, y)的计算式分别为：

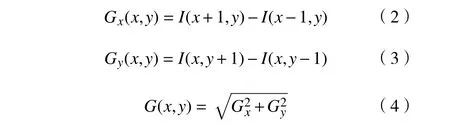
2）图像分割成大小相似的单元模式（Cell），以单元模式为主要统计单位来估计其梯度方向的质量分布图（Cell-HOG）。对于每个Cell计算梯度方向的质量分布图向量其中

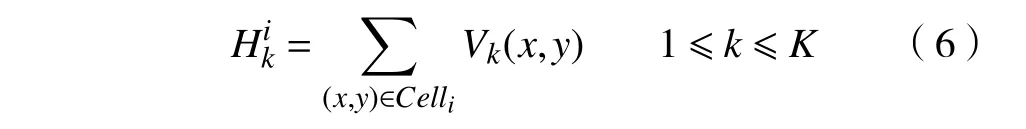
3）相邻Cell 组成一个块。该块在图像中向右或向下方移动一个Cell 以获得下一个块。

4）所有的块的梯度直方图融合起来，获得其最终输入图像的HOG 特征。

1.2.3 支持向量机（SVM）

SVM是由Vapnik 基于统计学习理论提出的一种机器学习算法，算法独特优势在于解决小样本、非线性问题。惩罚因子c 和核函数参数g 的选择会对SVM 模型最终结果起关键作用，参数寻优将关系到SVM 模型的优劣。网格搜索算法（Grid search,GS）是将c、g 在一定范围内划分网格，通过遍历网格内所有点来找到最优参数组合。

1.3 基于深度学习的振动图像分析方法

CNN 网络具有前馈结构，在图像分析中具有3个重要的特点：局部感知、权重共享和空间采样。CNN 典型结构由卷积层、池化层以及全连接层[15]构成。图2所示为典型的卷积神经网络结构图。

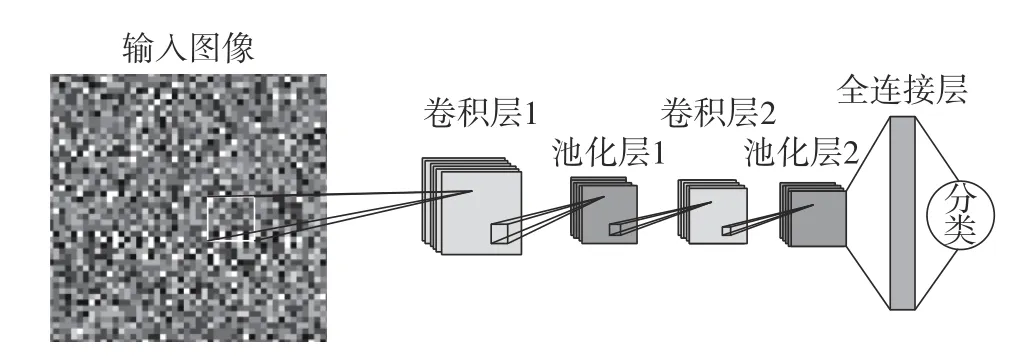
图2 典型的卷积神经网络

卷积层将输入图像与内核进行卷积。卷积层内核大小相同，提取图像局部特征。一般情况下，卷积过程中的数学模型表示为

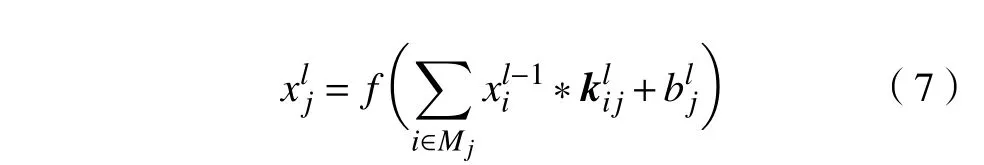
式中： xlj为l 卷积层j 通道的值；（*）为卷积操作；Mj为计算 xlj的特征图集；k 为S ×S 的核矩阵；f 为非线性激活函数； blj为偏置项。

池化层对于上一层输入的振动图像进行降采样处理，同时减少网络参数[16]。此外，池化层通过对输入进行小的变换保持了局部不变性，其数学模型为

式中：down（·）为子采样函数；β 为乘法偏置。

全连接层是一种传统的前馈神经网络，其目的是上层的特征图中收集所有的特征进行分类[17]，Softmax函数作为输出层激活函数。Softmax 函数定义如下

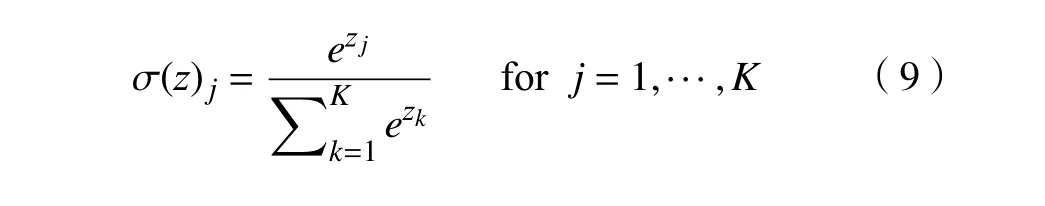
为了实现轴承振动信号多维信息特征的提取和分析，拟采用振动图像结合CNN的信息提取和建模方法对滚动轴承故障和质量等级评估等反映轴承质量品质的振动信号进行分析，轴承质量品质评估分析流程图如图3所示。

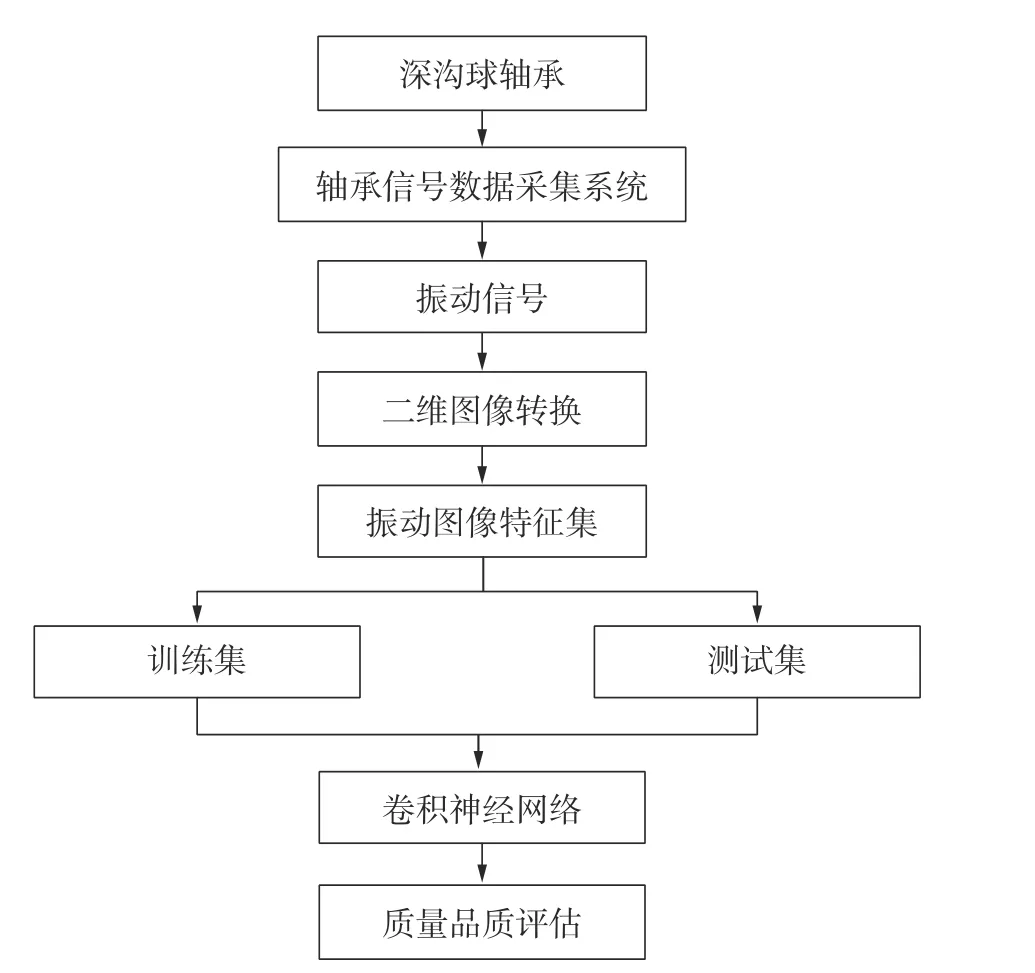
图3 轴承质量品质评估分析流程

该方法主要分为2个核心步骤：振动信号转换为振动图像和振动图像特征提取建模与分类识别。该方法的一般步骤如下：

1）采用振动信号采集系统依据国标[18]或行业推荐标准[19]采集轴承故障振动信号或不同品质轴承工作的振动信号；

2）利用1.1 节所述方法将振动信号转换为振动图像；

3）数据样本随机划分为训练集与测试集，训练集训练CNN模型，测试集评估模型精度，实现轴承故障诊断和质量品质评估。正确识别率CRR为

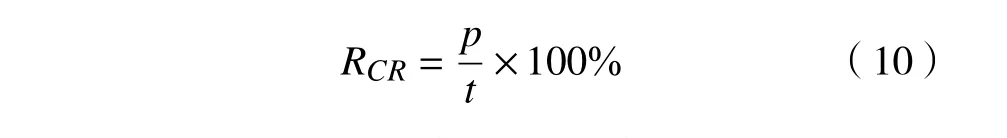
式中：RCR为正确识别率，RCR越高，表明模型越好；p为正确识别样本数；t 为总样本数。

2 实验部分

2.1 滚动轴承故障诊断振动信号分析

2.1.1 数据来源

为有效验证本文所提轴承振动信号分析方法，采用美国凯斯西储大学电气工程实验室提供的故障数据集[20]。以型号为6205-2RSSKF的轴承为研究对象，电火花加工单点损伤，电机负载为0HP、轴承转速为1797 r/min、采样频率为48 kHz 下进行试验。选取传感器在驱动端采集得到的4种状态（正常状态、内圈故障、外圈故障（6点钟方向）及滚动体故障）振动信号，总体样本数为200，样本信号包含2304个样本点。数据样本说明如表1所示。

2.1.2 基于振动信号的轴承故障诊断判别模型研究

1）VS-SVM 模型

直接采用SVM方法用于轴承故障诊断识别模型的构建，原始信号作为模型特征输入，SVM采用的核函数为径向核函数，通过GS寻优方法获取最优值，参数c、g 寻优范围[2-20,220]。将滚动轴承4种状态的振动信号直接建模，随机选取120样本作为训练集用于故障诊断模型的建立，其余样本用于验证模型，随机10次样本划分并建立SVM 模型，优化得惩罚因子c为0.41，核函数参数g 为0.04，训练集平均识别率为100%，测试集平均识别率为95.62%。

2）VSTF-SVM 模型

振动信号包含丰富的相关轴承故障信息，通过提取振动信号的时域特征，采用优化参数的SVM进行轴承故障诊断识别模型构建。利用统计方法提取16个时域特征，200个样本按3∶2比例划分训练集与测试集进行模型训练与验证。模型优化后c =8，g =0.25，随机10次样本划分后获得训练集平均识别率98.82%，测试集平均识别率97.25%。

2.1.3 基于振动图像和卷积神经网络的轴承故障诊断判别模型研究

依据1.1节方法将样本振动信号转化为48×48的振动图像，图像样本如图4 所示。由图看出正常状态的振动图像与其他3种状态振动图像差别明显。

图4 4种状态轴承振动图像

1）VI-HOG-SVM 模型

为克服在振动信号中提取特征时不能很好挖掘轴承工作特征信息，将振动信号转换为振动图像，利用HOG 算法获取振动图像的图像特征，使用SVM分类器对轴承故障进行诊断识别。样本训练集与测试集按3∶2划分并进行特征提取并建模分析，随机10次样本划分建模分析获得训练集平均识别率为100%，测试集平均识别率为99.62%。最优模型参数c =5.66，g =0.004。

2）VI-CNN 模型

按上述比例随机划分样本数据，设置2层卷积与2层池化。卷积层参数分别设置[21-22]为：50@3×3，100@2×2，步长均设为1，使用ReLU 激活函数。池化层均采用2×2，步长设置为2的最大池化。随机10次样本划分后训练集与测试集平均识别率均为100%。

2.1.4 最优故障诊断模型分析

图5和表2所示为采用随机分组方式进行样本划分后，对每种振动信号分析方法建立10个模型的计算结果。

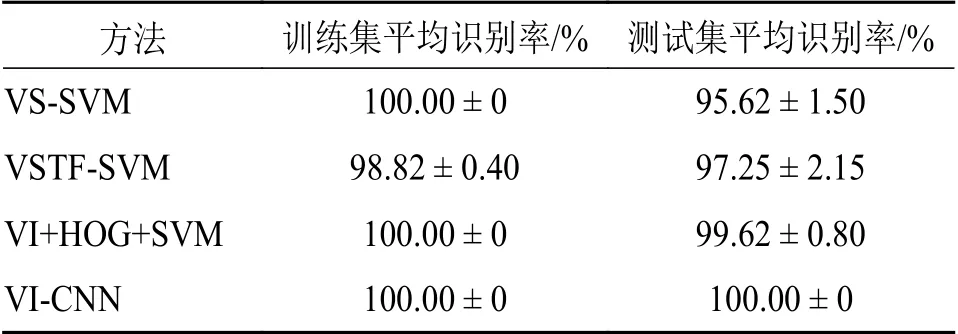
表2 轴承故障识别结果统计

图5 轴承故障识别结果比较

由图5 可知，VI-CNN 方法得到了最高的CRR 值，且10个模型的CRR值均为100%；VI-HOG-SVM模型的CRR 次之，为99.62%；VSTF-SVM 模型的CRR 为97.25%；VS-SVM方法的分析结果最低，且10个模型的测试结果差异较大，表明该方法具有较低的稳健性。直接采用振动信号结合SVM 方法较难提取分析信号的深度特征信息；VI-CNN 模型相比于其它方法具有更好的细节信息分辨力和信噪分离能力，模型具有较好的分析精度和稳健性。

VI-CNN 模型最佳结果混淆矩阵如图6所示，由图可知该模型平均测试精度为100%，每一类分类识别率均为100%，表明VI-CNN 模型可以实现振动信号信息特征的有效且多维度提取，可以实现更好的识别结果。

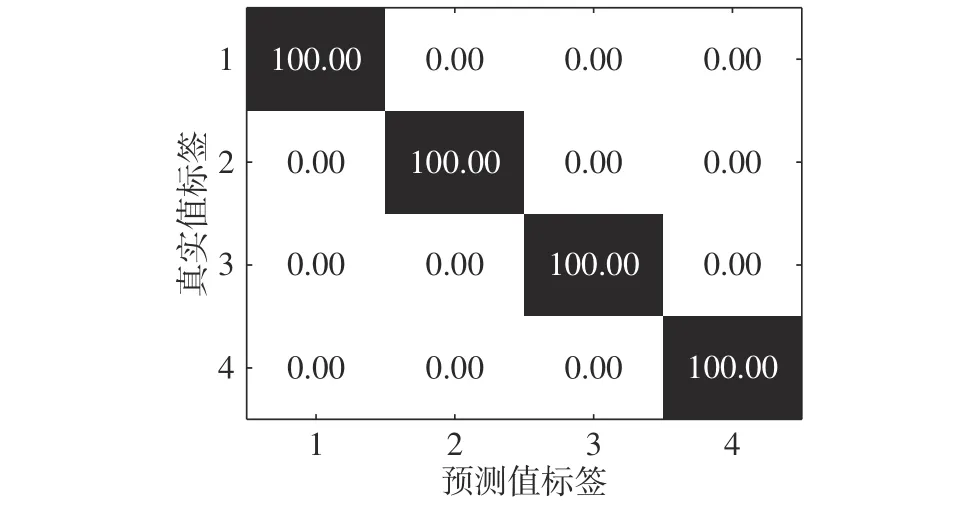
图6 VI-CNN 模型最佳结果混淆矩阵

2.2 滚动轴承质量等级评估振动信号分析方法

2.2.1 数据来源为进一步验证所提方法的优势，依据《JB/T 7047-2006中深沟球轴承振动水平标准》，采用S0910装置依据机械行业推荐标准-深沟球轴承振动水平采集得优等品、一等品及合格品轴承振动信号。振动信号检测装置如图7所示。主轴转速为1800 r/min，轴向载荷70 N，采样频率为8 kHz。每一等级样本各50个，样本信号包含2304个样本点。图8所示为3种品质轴承振动信号。

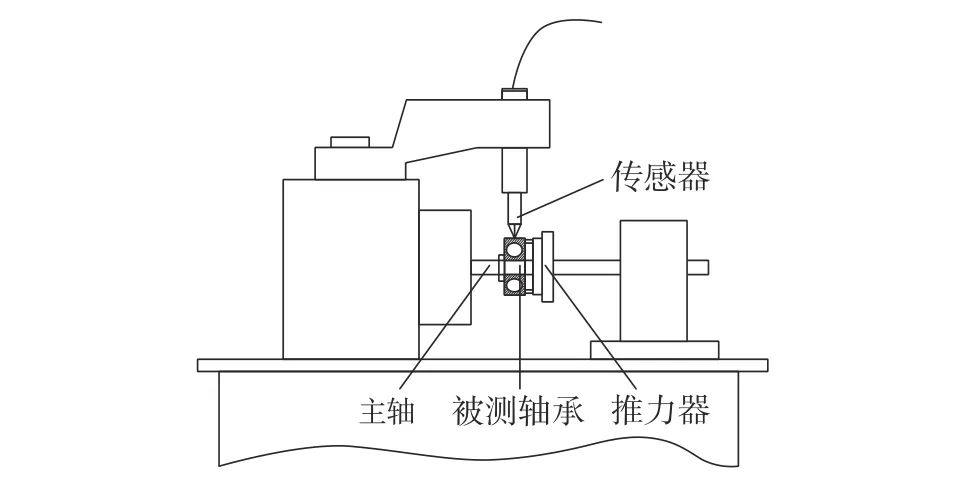
图7 轴承检测装置简图

图8 3种品质轴承振动信号图

2.2.2 基于振动信号的轴承质量等级评估模型研究

随机选取90个振动信号样本作为训练集，60个作为测试集。

1）VS-SVM 模型

直接采用优化参数的SVM进行建模与轴承质量等级评估，随机10次样本划分后训练集平均识别率为100%，测试集平均识别率为84.83%。优化后模型参数c=1，g =0.71。

2）VSTF-SVM 模型

使用振动信号16个时域特征并结合SVM进行建模与轴承质量评估，随机10 次样本划分后训练集平均识别率为97.77%，测试集平均识别率为86.66%。模型参数c=22.63，g =0.18。

2.2.3 基于振动图像和卷积神经网络的轴承质量等级评估模型研究

依据1.1节所提方法，样本信号转化为48×48的振动图像，振动图像如图9所示。由图9可知优等品与一等品、合格品振动图像有明显差别将振动图像样本随机分为90个训练集样本和60个测试集样本。

图9 3种轴承品质的振动图像

1）VI-HOG-SVM 模型

轴承质量等级样本训练集与测试集进行特征提取并建模与预测识别，随机10次样本划分建模分析获得训练集平均识别率为100%，测试集平均识别率为95.83%。最优模型参数c = 4，g = 0.0055。

2）VI-CNN 模型

振动图像根据节1.1方法由振动信号转换，分别设置2层卷积与2层池化，卷积层参数分别设置为：50@3×3，150@2×2，步长均设为1，使用ReLU 激活函数。池化层均采用2×2，步长设置为2的最大池化。随机10次样本划分后训练集平均识别率为100%，测试集平均识别率均为98.16%。

2.2.4 最优判别模型分析

对轴承质量等级评估实验数据样本随机划分后，每种振动分析方法分别建立10个模型评估识别结果，如图10所示。由图可以看出，VI-CNN 模型平稳性最好，其他3个模型轴承质量评估识别结果波动比较大。表3中计算得到10次VI-CNN 模型的CRR 平均值为98.16%，标准差为0.49；VI-HOGSVM 模型CRR平均值为95.83%，但CRR值标准差为2.49，标准差值过高，其余2个模型CRR值均低于90%，且由标准差值可以看出模型稳定性较差。VI-CNN 模型在轴承质量等级评估过程中，表现出更好的样本特征信息提取能力，模型精度更高。

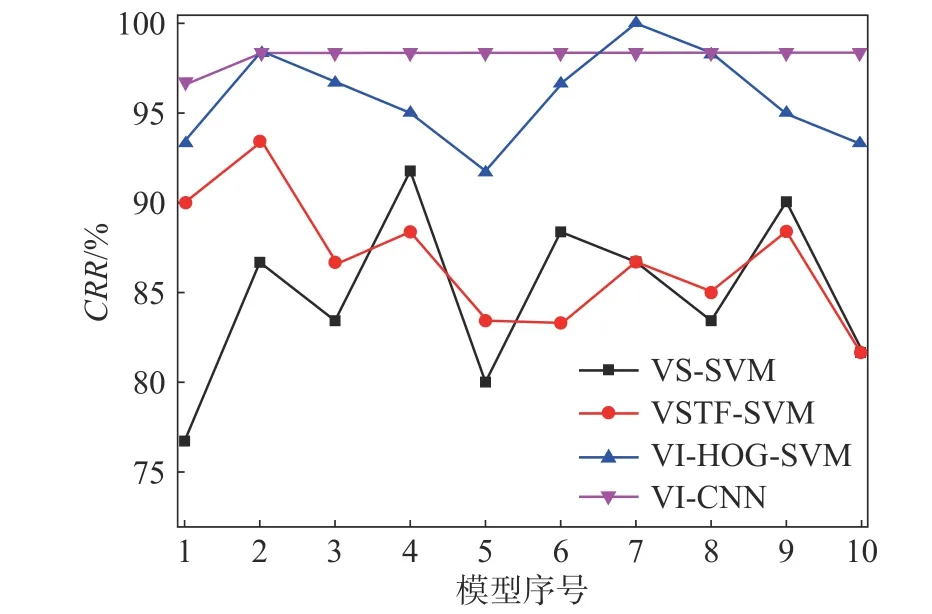
图10 轴承质量等级评估结果比较

表3 轴承质量等级评估结果统计

对于轴承质量等级数据集，VI-CNN 模型识别结果混淆矩阵如图11所示。标签1、2、3分别代表优等品、一等品、合格品，行代表测试值标签，列代表真实值标签，在进行轴承等级识别分类时错将某一优等品样本识别成一等品样本，导致平均测试识别精度为98.33%。对于不同质量等级的轴承振动信号样本数据，该模型仍能高效稳定识别。