输油管道内检测机器人结构设计与仿真*
2022-02-13孙乐辰万菁菁杜天昊
孙乐辰 万菁菁 杜天昊 杨 峰
(1.北京交通大学机械与电子控制工程学院 2.中国石油化工股份有限公司胜利油田分公司东辛采油厂)
0 引 言
服役于石油运输的管道长期处于水、油及其混合物以及硫化氢等环境中,极易发生电化学腐蚀。同时,随着输油管道服役年限的延长,裂纹、错位等缺陷也会产生。为了避免管道事故的发生,必须对其定期进行检测[1-2]。目前国内大型油田的例行检测都采用外检测法对管道接口处的焊缝进行检测。因为输油管道一般埋于地下,检测成本和维修成本均很高。相较于大型的油气管道,小直径的输油管道检测难度更大。为了对常用型号的输油管道进行快速、准确的检测,设计一种能够在管道中自主运行、适应复杂环境、搭载检测设备并适用于各型号输油管道的检测机器人具有重要意义。
目前国内外对于金属管道常用的检测方法主要包括:超声波检测技术、漏磁检测技术、X射线检测技术及视频图像检测技术等。超声波检测技术具有对管道性能无影响、受外干扰程度小、检测准确、设备轻便以及检测效率高等优点,将作为本设计的检测方式。现有石油管道机器人主要驱动方式包括被动式和主动式,其中被动式机器人依靠管道中石油的流动被动运动。北京航空航天大学的张逍[3]设计了一种由万向轮连接具有高自由度的管道检测机器人,但这种机器人的结构冗杂度高且被动驱动的方式稳定性较差。主动式管道机器人有较多的结构,其中包括轮式、履带式及蠕动式等。其中轮式的结构灵活方便,但和管壁摩擦较小,在油气管道中难以适应环境。较为经典的轮式结构机器人有张永顺等[4]研究的直进轮式全主动管内移动机器人。相对于轮式,蠕动式机器人应用更加广泛,其通过交替重复的收缩和伸长方式向前行进,越障性能优越,但能量损失大且牵引力小,例如德国的B.KLAASSEN等[5]研制的采用电动机驱动6单元体的蠕动式管道机器人。履带式结构的机器人牵引力大、越障能力强,但结构复杂。笔者采用主动驱动的同步轮带式结构,集成了履带式和轮式的优点,其结构简单且牵引力较强。同时基于超声波检测技术,设计一种能够自主独立运行,搭载检测设备,保证较大范围变径及适应较小直径管道的内检测机器人。
1 输油管道超声波检测原理
超声波是一种频率大于20 kHz的弹性机械波,其检测方法有很多,应用最广泛的是A型脉冲反射法。A型显示是用点扫描方法分析系列波信号的幅值与时间的关系,并显示在直角坐标系中。脉冲反射法中超声波发射后,其经过不同介质所形成的界面时会发生反射。本文的超声检测模块利用了A型脉冲反射法[6],图1为超声波检测原理图。其中T代表发射脉冲信号,F代表缺陷回波信号,B代表底面回波。当探头发射脉冲信号,超声波经过声耦合介质进入管道中,若无内部裂纹缺陷,超声波会直接到达材料底面,并反射回到探头接收器中(见图1a);若存在内部裂纹,则有部分超声波能量在缺陷处反射,提前回到探头中(见图1b);若存在腐蚀缺陷,腐蚀将导致待测件的厚度减小,使超声波在材料中的反射距离变短,从而导致T信号与B信号从发射至返回时间间隔变短(见图1c)[7]。

1—探测仪;2—待测件;3—内部裂纹;4—腐蚀缺陷。
2 机器人整体结构设计
2.1 设计要求
我国输油管道常用规格(外径×壁厚)为:DN100(114 mm×7 mm)、DN150(159 mm×9 mm)、DN200(219 mm×9 mm)、DN250(279 mm×9 mm)、DN300(325 mm×10 mm)。设计机器人可凭借自身动力在管道中行进,同时利用超声波探伤对管壁上的腐蚀、裂口、错位、障碍物等多种缺陷进行探测并记录缺陷位置。设计包含以下模块:驱动模块、变径模块、超声波检测与定位模块。设计流程见图2。

图2 机器人设计流程图
2.2 整体结构组成说明
机器人结构主要包括驱动模块、变径模块、超声波检测模块和定位模块。其中驱动模块使用同步带和同步带轮提升了机器人运动时的稳定性和越障能力;变径模块使用了基于滚珠丝杆的升降式变径机构,其结构简单易于控制且调节范围大,能使机器人适应不同管径的石油管道;超声波探测模块使用了一种原创的双弹簧伸缩、喷探一体式的超声波探头,能一定程度上实现全自动化的管壁缺陷探测;定位模块则采用计数齿轮和计时器2种方式同时计数,规避了GPS等坐标系统定位方式可能会出现的信号和精度问题。整机结构如图3所示。

1—驱动模块;2—变径模块;3—超声波检测模块。
2.3 驱动模块
管道机器人的主要运动方式包含蠕动式、蛇形、多足式、轮式、履带式及螺旋前进式等[2-8]。其中轮式又包括支撑轮式与车型式。而蠕动式、蛇形、多足式运动方式具有运动效率低、行走不连续、稳定性较差且运动自由度较为冗杂等缺点,不适用于执行输油管道内连续进行的检测任务。因此,本文将重点对比轮式、履带式以及螺旋前进式在携带检测仪器、结构与越障方面的性能。
轮式、履带式及螺旋前进式3种类型驱动机构都具有较强的驱动能力并且都便于携带检测仪器。但是对于运动效率而言,螺旋式的性能与另外2种相比明显不足。在结构方面支撑轮式最为简单,其次是螺旋式,履带式结构较为复杂。对于需要在管道探测中重点考虑的越障和弯道通过性能,螺旋驱动式对比另外2种都有明显不足。履带式在越障性能上优于支撑轮式,但在弯道通过性上稍有不足。
综合对比3种驱动机构的优缺点,结合设计要求中管径以及行走距离较长和需要搭载检测装置的要求,选择对轮式和履带式进行改进以作为驱动方式。由于支撑轮式结构在越障性能上有所欠缺,所以,使用同步带与同步带轮来增强驱动结构的越障能力。同步带传动综合了带传动、链传动和齿轮传动的优点,具有传动准确、工作时无滑动、传动平稳的特性,而且具有缓冲和减振能力,噪声低,传动效率高,节能优势显著。转动时,通过带齿与轮的齿槽相啮合来传递动力。同步带传动传输具有准确的传动比,无滑差,可获得恒定的速比,传动平稳,能吸振,传动比范围大,一般可达1∶10。
由于管道尺寸限制,拖拽电缆的驱动模块所受阻力会大大增加,进而影响检测性能,所以采用6 V直流电源驱动电机来为机器人行进提供驱动力。为了尽可能地节约空间,将驱动电机集成在驱动模块壳体内部,通过一对锥齿轮进行转动方向的转换。有源驱动电机采用低压无刷直流伺服电机,该类驱动电机具有质量轻、体积小、牵引力大等优点。该电机还配备有编码器等,既便于对其进行控制,又便于后续定位装置的设计。为确保速度符合要求,电机前端使用180行星齿轮箱进行减速,减速比为370。电机具体参数为:额定电压6 V,额定转速16 r/min,额定力矩15 N·cm,质量0.069 kg,箱体长度29.9 cm。驱动模块结构如图4所示。
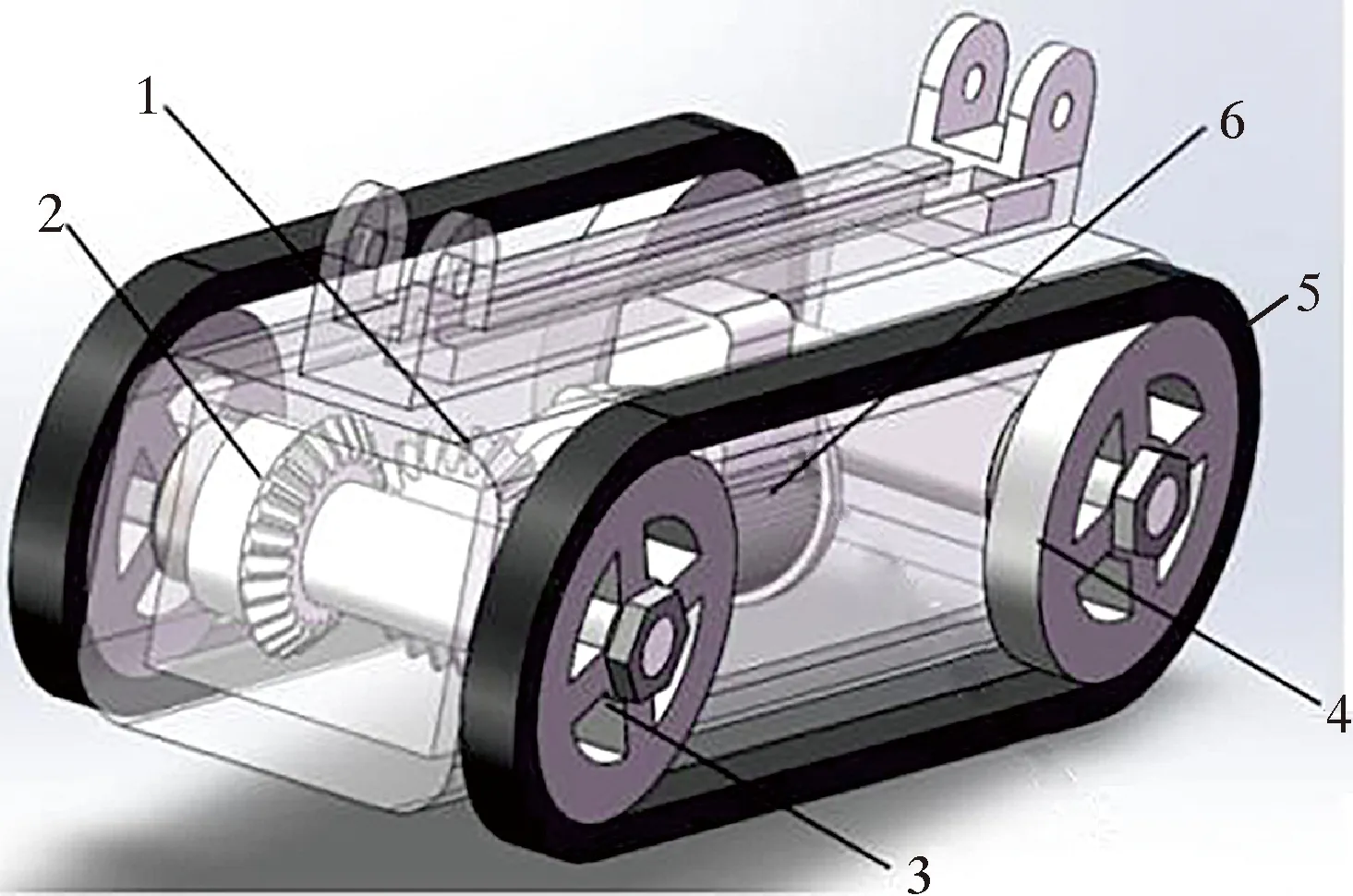
1—主动锥齿轮;2—从动锥齿轮;3—主动轮轮毂;4—被动轮轮毂;5—同步带;6—驱动电机及支撑座。
驱动模块的基本参数如表1所示。为了更好适应DN100和DN150这2种较小管径输油管道,驱动模块设计为可拆卸装置,所使用的同步带轮半径和驱动模块密封箱截面面积可减小至通用尺寸60%。结合所使用的180行星齿轮减速电机,可以设定该机器人的额定行进速度为5 cm/s,单次检测时间(1 km管道)为5 h。

表1 驱动模块关键参数 mm
为防止整个装置动力不足并解决支撑的问题,一共采用了3组驱动模块。每1个驱动模块包含2组同步带与带轮。为确保摩擦力足够大,同步带以钢丝绳为强力层,外覆以聚氨酯橡胶的环形带,通过活动支架配合变径用滑块滑轨将整个驱动模块垂直压在管壁上,使其可以与管壁完全相切。管道检测机器人整体截面如图5所示。
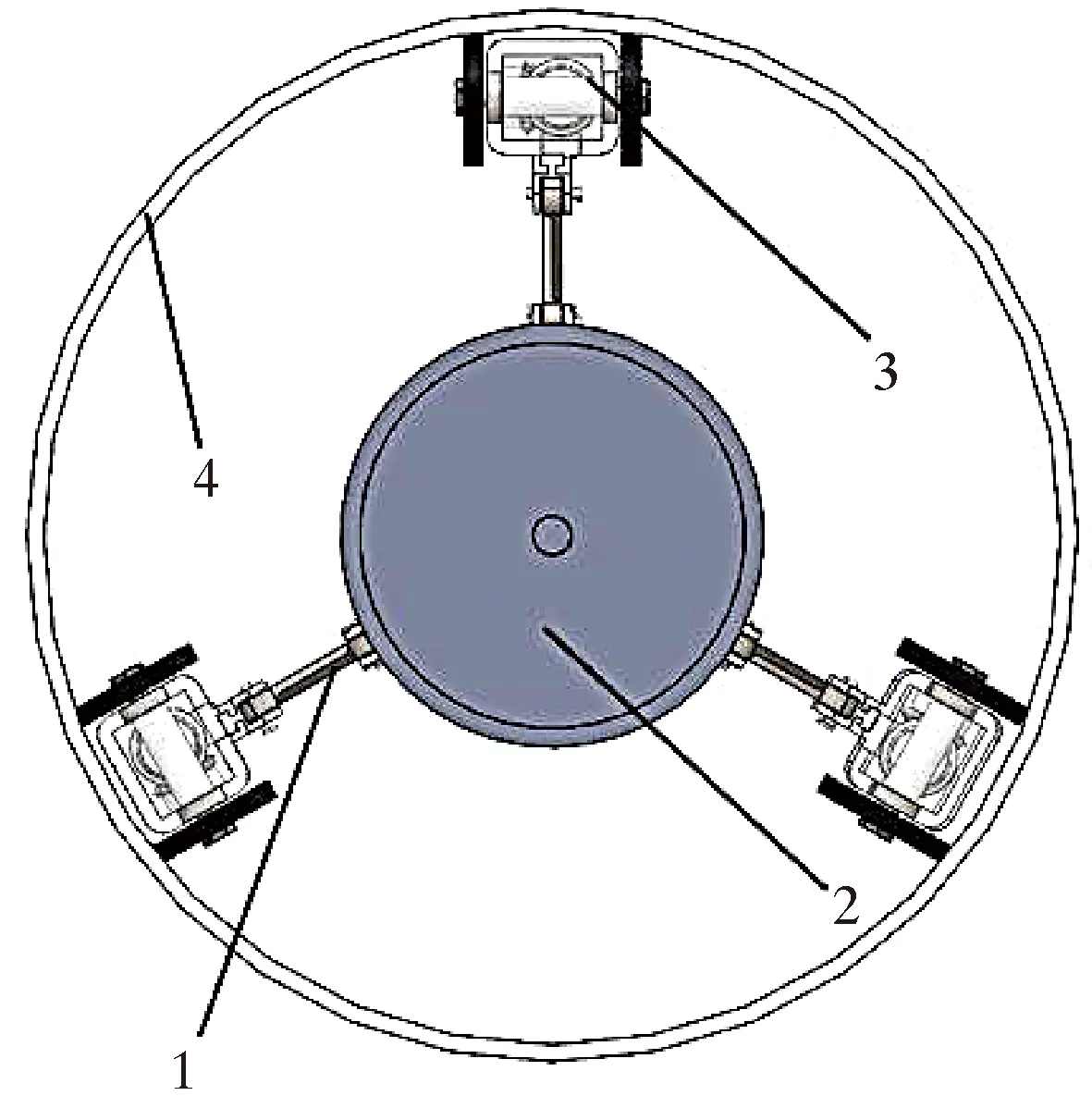
1—活动支架;2—机器人主体;3—驱动模块;4—管道(ø273 mm×9 mm)。
2.4 变径模块
针对需要保证机器人能够适用于不同规格输油管道的设计要求,能够实现大幅度变径的结构是必不可少的重要机构。设计变径机构的目的是在管道内径发生变化时,它能主动或者被动调节管道机器人驱动模块的位置并使其能够保持与管壁的接触,从而保证机器人在管道中的正常行进。
一般来说,变径机构主要分为主动变径机构和被动变径机构。被动变径模块可由弹簧等实现,主要功能是缓冲和微调等。主动变径模块有升降式、蜗轮蜗杆式以及丝杠螺母式变径机构[2-9]。考虑到涡轮蜗杆式变径机构刚度较低,传动效率低,同时丝杆螺母式变径机构可调范围比较小,最终选用基于升降式变径机构配合活动支架与滑块滑轨来进行变径。
变径模块结构如图6所示。伺服电机会带动丝杆旋转,从而推动升降平台向左运动。升降平台与固定平台通过活动支架与装在驱动模块上的滑轨固定端以及滑轨移动端相连。当活动平台向左运动时,由于活动支架对力的传递,移动滑块会向左移动,两活动支架间夹角θ减小,滑块固定端到丝杆的垂直距离d增大,从而实现周向尺寸的改变。同时,在驱动模块上安装有力传感器,对伺服电机进行负反馈控制。设置最小压力值Nmin,当压力值N≥Nmin时,力传感器输出高电平信号,即

1—伺服电机;2—活动支架;3—滑块移动端;4—滑块固定端;5—丝杆;6—固定平台;7—升降平台。
A1&A2&A3=1
(1)
式中:A1、A2、A3分别为3个驱动模块上力传感器输出的电平信号。此时,伺服电机停止工作,变径过程完成。
同时为了保证机器与管壁贴合的紧密性,在力传感器中增加一个最大压力值Nmax。当某一个压力大于Nmax且仍有力传感器未达到最小压力值Nmin时,表明此时变径机构未能准确贴合管壁,需要人工调整角度再次进行变径。
变径模块使用扭矩数字电机,额定电压为4.8 V,额定转速0.14 r/min,额定转矩109 N·cm,质量为0.069 5 kg。变径模块关键参数如表2所示。

表2 变径模块关键参数 mm
2.5 超声波检测模块
超声波检测分为静态超声波检测和动态超声波检测。考虑到管道机器人负载的限制,对探头数量要有所限制。为了保证管道检测的全面性,采用动态超声波检测方法。管道机器人的超声波检测模块共有3个超声波探头,沿机器人的周向均布。当机器人运动时,3个探头在步进电机驱动下旋转。
利用超声波探头检测时,需要保证探头能够紧贴管壁,同时需要探头与被测管壁之间没有空隙[10],因此耦合剂喷头与变径装置的设计十分关键。由于3个超声波探头须要同时实现变径,所以设计了利用1个大直径锥齿轮带动3个小直径锥齿轮运动的探头伸缩装置,如图7所示。当下方步进电机驱动大直径锥齿轮逆时针转动时,与其啮合的3个小锥齿轮都会沿顺时针方向同步转动,驱动丝杆旋转,从而带动2件升降杆向外顶出,保证探头能够与管壁贴合。
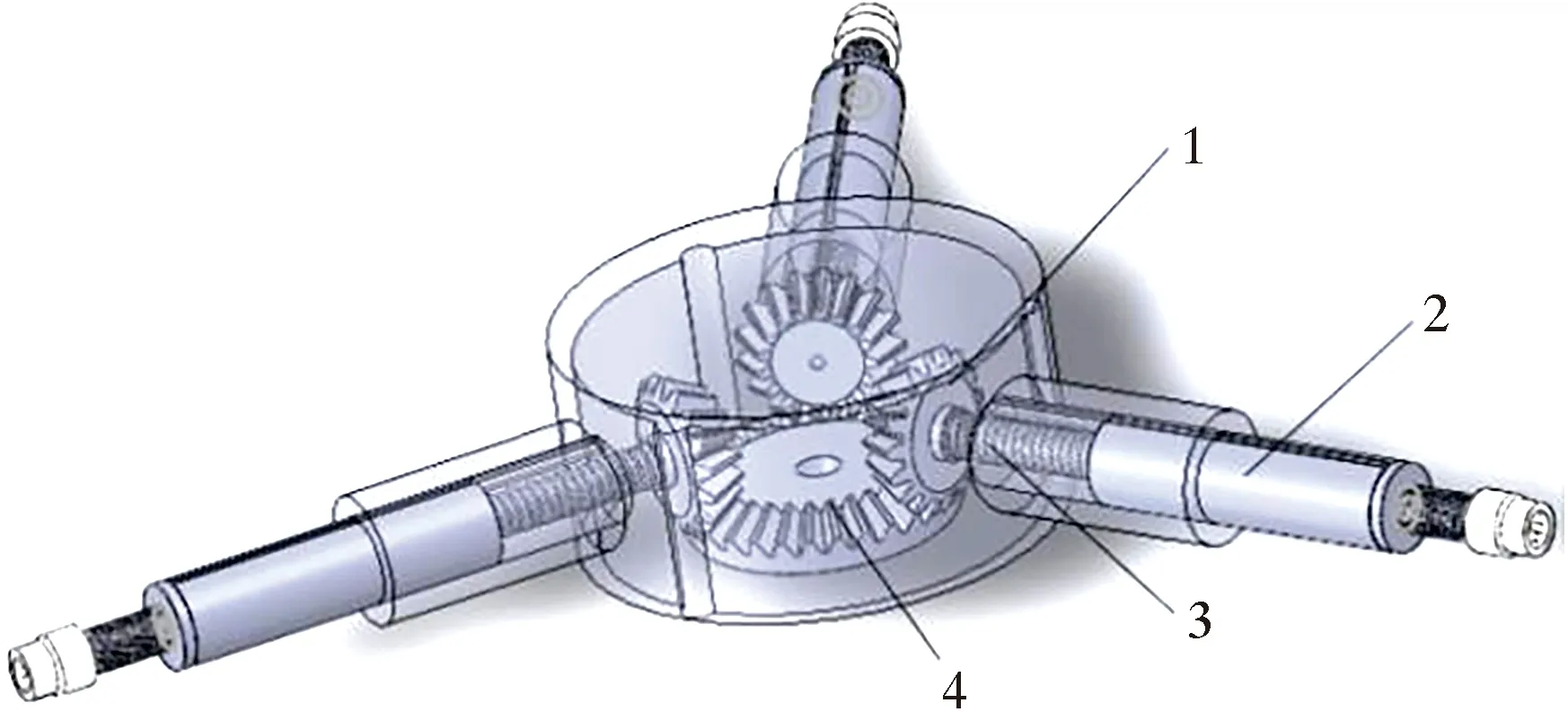
1—小直径锥齿轮;2—升降杆;3—丝杆;4—大直径锥齿轮。
若探头与管壁不能完全接触(即存在空气),则会大大影响检测的精度。单个超声探头截面如图8所示。从图8可以看出,大弹簧连接耦合剂喷头,大弹簧内部的小弹簧连接超声波探头。当滚珠丝杆转动带动升降杆伸长时,耦合剂喷头先接触管壁,此时大、小弹簧同时开始被压缩,当压缩量均为ΔL1时,大弹簧压阻式力传感器设置最小压缩力,则有:

1—小弹簧(连接超声波探头与升降杆);2—大弹簧(连接耦合剂喷头与升降杆);3—耦合剂喷头;4—超声波探头。
(2)
耦合剂喷头开始喷出耦合剂。耦合剂喷孔均匀分布在耦合剂喷头内壁上,从而保证探头与管壁间不存在空气并提升耦合剂的利用率。当压缩量均为ΔL2时,大弹簧压阻式力传感器设置最大压缩力:
(3)
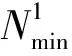
耦合剂喷头停止工作。当超声波探头能检测并反馈数据后,导出此时压阻式力传感器上测出的压缩力Nc,可以通过该数据获得管道的精确内径。

2.6 定位模块设计
当探测出油管中缺陷时,需要进行定位。输油管道一般埋于地下并且为金属材质,利用GPS定位会出现信号不稳定、定位精度较差的问题[3]。为了能够对缺陷位置进行准确定位,同时采用2种较为常见的定位方式。
第1种为里程轮计数法。假设检测到缺陷m时计数齿轮转动次数为n,则该机器人此时运动里程计算式为:
X1m=2πRn
(4)
式中:X1m为利用里程轮计数法测得缺陷m时的运动里程,cm;R为同步带轮半径,cm;n为检测到缺陷m时计数齿轮转动次数。
由于机器人在石油管道中可能发生打滑现象,实际运动里程Xm可能小于测得缺陷m时里程X1m。
第2种方式通过时间进行定位。机器人配备速度传感器,相关计算式为:
ve=2πRω
(5)
式中:ve为机器人额定运动速度,cm/s;ω为同步带轮转动角速度,rad/s。
当机器人运动到达额定速度ve并保持匀速运动时,计时器开始计时,当速度变化超过极限值(该数值应在样机多次试验基础上分析数据给出)时,计时器停止计时直至速度恢复到允许区间。假设检测到缺陷m所用时间为t,则可近似得到此时运动里程计算式为:
X2m=2πωRt
(6)
式中:X2m为利用时间定位法测得缺陷m时的运动里程,cm;t为检测到缺陷m时所用时间,s。
由于加速阶段与遇到障碍等时间不计,实际位置Xm可能大于X2m。
根据2种定位测量方式,可采用加权平均的方式得出较为准确的数据,即
Xm=0.5(aX1m+bX2m)
(7)
式中:参数a和b为通过试验测量的权重常数,无量纲。
3 机器人关键参数计算
3.1 变径模块关键参数
图9为单变径模块关键几何参数示意图。其中:l为活动支架连杆的长度;h1为升降平台初始位置距固定平台的距离;d表示升降平台移动的距离,h2为丝杆中轴线和滑块移动端的距离;α为单根活动支架与管道轴线的夹角,并随着d的变化而变化。
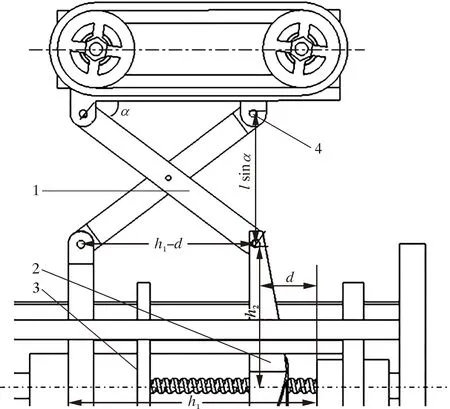
1—活动支架连杆;2—升降平台;3—固定平台;4—滑块移动端。
通过几何关系的分析,首先可以得到α和d的关系式:
(8)
因为滚珠丝杆连接的升降平台进行匀速升降运动,故可以得到:
d=vt
(9)
结合式(8)、式(9),得出活动支架的角速率和变径速率分别为:
(11)
式中:ω为活动支架的角速率,rad/s;v0为活动支架的变径速率,mm/s;v为升降平台运动的速度,mm/s;t为升降平台运动的时间,s。
已知升降平台的运动速度v和滚珠丝杆的导程S1,可以得到控制丝杆的伺服电机转速n1;若伺服电机的功率恒定为P,则同时可得其扭矩T:
(12)
(13)
式中:n1为电机转速,r/min;S1为滚珠丝杆导程,mm;P为伺服电机功率,W;T为电机扭矩,N·m。
3.2 超声波检测探头模块关键参数
图10为超声波检测模块中圆锥齿轮的结构示意图。两轮的传动比和角速度与齿轮本体几何尺寸参数的关系为:

图10 超声波检测模块直齿圆锥齿轮结构示意图
(14)
式中:i12为传动比;ω1、ω2为控制大、小锥齿轮的伺服电机的角速度,rad/s;d1、d2为大、小锥齿轮分度圆直径,mm;δ1、δ2为大、小锥齿轮分度圆锥角,(°)。
由式(14)可得:
(15)
(16)
已知小锥齿轮连接的丝杆的导程为S2,可以推导出超声波探头的运动速度v2计算式为:
(17)
3.3 机器人最小过弯半径
通过机器人的总长度和宽度可以计算出其最小可通过弯道的曲率半径。图11为机器人通过弯道时的轮廓和几何参数示意图。其中:L为机器人的长度;h为机器人的直径;R0和r0分别为管道外侧和内侧对应的曲率半径。已知管道的直径为D,可以得到下列关系式:
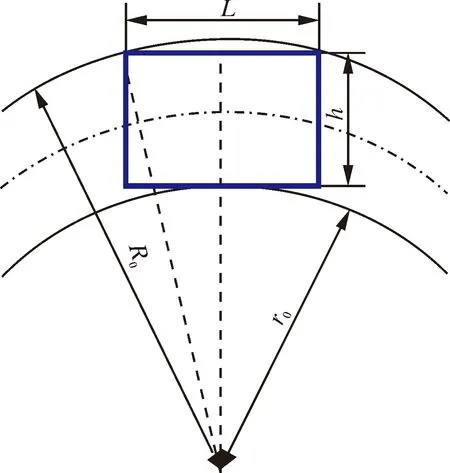
图11 机器人通过弯道示意图
D=R0-r0
(18)
由图11与式(18)可以得到以下方程:
(19)
式中:L为机器人的长度,mm。
最终求得最小可过弯的管道外侧曲率半径为:
(20)
式中:h为机器人的直径,mm。
在Solidworks模型的设计参数中,机器人最大直径hmax≈318 mm,最小直径hmin≈110 mm,L≈213 mm,可适应的管道直径D的范围为114~325 mm。分别将最大管道直径和最小管道直径代入式(20)可以得到:R0≈813 mm和1 891 mm。
由此可知,在管道直径最大时机器人的最小过弯半径为813 mm,在管道直径最小时机器人的最小过弯半径为1 891 mm。
3.4 机器人超声波检测探头轨迹覆盖率
超声波探头移动速度示意图如图12所示。从图12可见,超声波探头的移动速度由2个方向的速度分量组成,一个是沿管道方向的vh,另一个是与管壁相切方向的vt。若将整个管壁在平面上展开可以发现,探头在2个相互垂直的方向分别做匀速直线运动和往复直线运动。假设探头在往复运动部分的加、减速时间极短并满足匀速运动时的速度大小均为vt,则探头的探测范围是以探头和壁面接触点为圆心,直径为d0的圆面。图13为探头在管壁平面展开图上两个运动周期的轨迹和探测范围示意图。
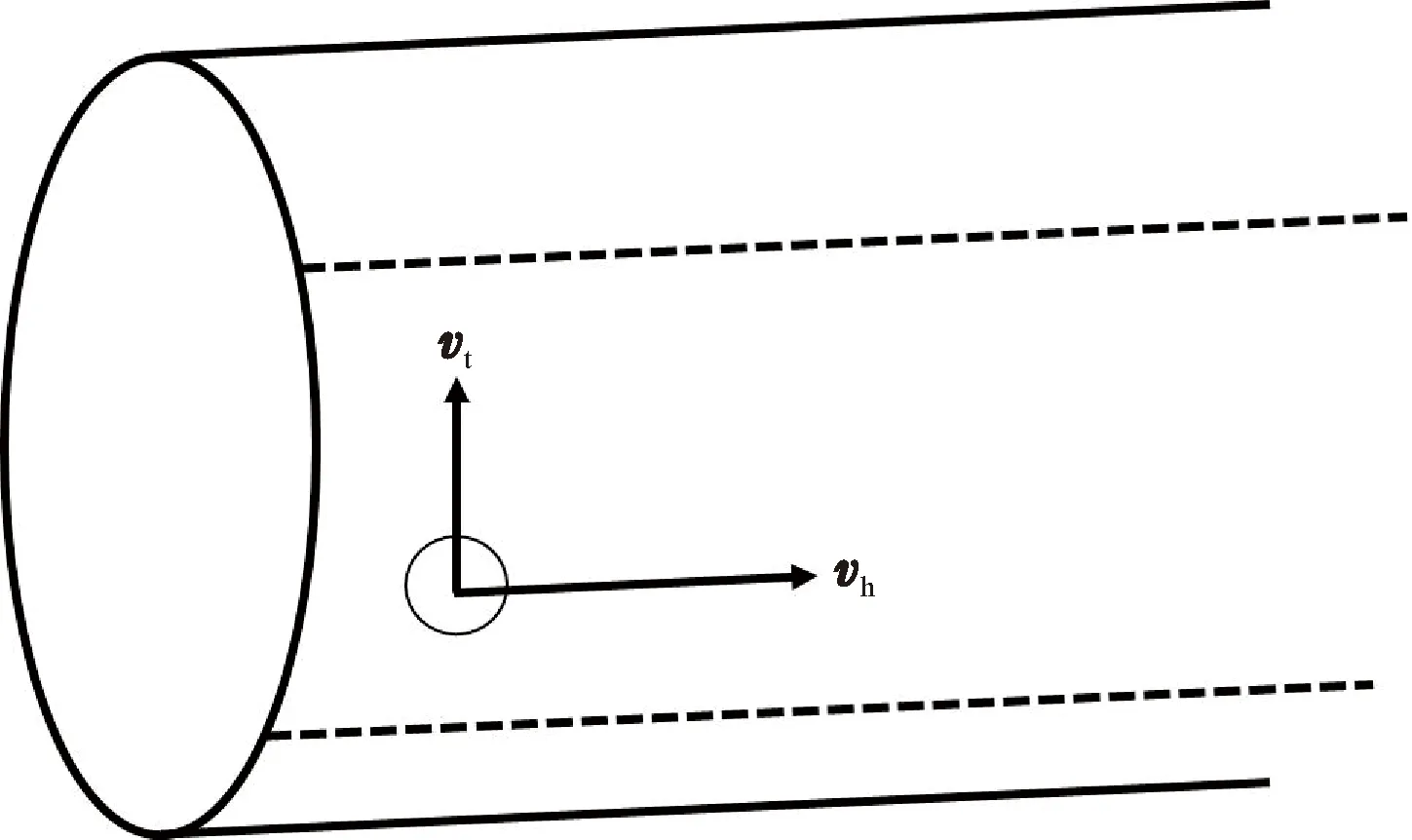
图12 超声波探头移动速度示意图

图13 轨迹和探测范围示意图
已知管道的直径,检测探头移动线速度vt,可以得到步进电机的转速计算式:
(21)
式中:nm是步进电机转速,r/min。
(22)
单个探头在一个周期内沿管道方向的运动距离L1计算式为:
(23)
根据几何关系,半个周期内的未检测区域的面积Au计算式为:
(24)
式中:d0为以探头和壁面接触点为圆心的圆形探测范围直径,mm。
单个探头一个周期的期望检测面积A计算式为:
(25)
最终计算总的被检测概率Pj为:
100%
(26)
为了提高单次检测的覆盖率,行进速度vh调节为5 cm/s,nm约为0.2 r/min,d0=50 mm,代入式(26)可得缺陷总被检测概率为84%。
4 基于COMSOL的超声探测仿真
4.1 待测件的几何建模和参数设置
当物体某个部分受力时,该处会发生弹性变形,能量会以波的形式向周围扩散,整个物体也会发生变形,这个传播过程需要用固体力学中弹性动力学模型解释[11-12]。基于COMSOL的有限元仿真可以利用固体力学模块和压力声学模块的耦合,可视化地模拟待测件在被探测过程中超声波的传播规律,以验证超声波检测的可行性。
为了简化仿真模型、提高有限元软件的分析效率,可以将超声波在石油管道材料中的传播问题转变为平面应力问题,因此可以将石油管道设计为二维截面模型。同时为了使超声波传播过程更加清晰,选取截面一小部分进行分析。管道截面二维仿真模型如图14所示。将圆弧几何结构简化为矩形结构,内部缺陷是长宽比为3∶1的矩形,表面腐蚀设计为部分厚度减小的几何结构。
图14 仿真二维几何模型
在软件的参数设置中,待测件材料使用碳素结构钢,置于空气域中。对于超声激励信号的选择,采用一个周期的5 MHz正弦震荡信号[13-14],并经过Hanning窗进行调制,最终得到表达式为:
(27)
式中:F为t时刻的信号值,无量纲;f为震荡信号的频率,MHz。
为了减少简化模型对超声波传播的影响,需要将矩形的两个侧边设置为低反射边界,其余为自由边界。
4.2 仿真结果分析
图15为该管道机器人超声波检测仿真的流程。首先耦合剂喷头伸长到设计长度时,喷头紧贴住管壁开始喷出耦合剂。当超声波探头伸长到设计长度时,耦合剂喷头停止工作,此时信号接收装置收到反射回的声波并进行判断。若判断为缺陷,则将读取里程轮与计时器中数据,储存在内置储存卡中。图16为仿真软件中探头与待测输油管道管壁的接触结构。

图15 超声波检测的流程

图16 管道机器人超声波探头与管道接触仿真结构
对于信号处理模块单元,本文对3种不同情况下的信号接收装置接收到的超声波信号进行了物理场仿真。预处理后,建立物理场对待测件进行研究计算。图17是超声波在完好管道工件中的传播图。其中:图17a为传播初始阶段;图17b中,超声波在1.7 μs时到达底面;图17c中,超声波发生在接触底面后反射;图17d中,反射后的波在3.3 μs时回到激励处。
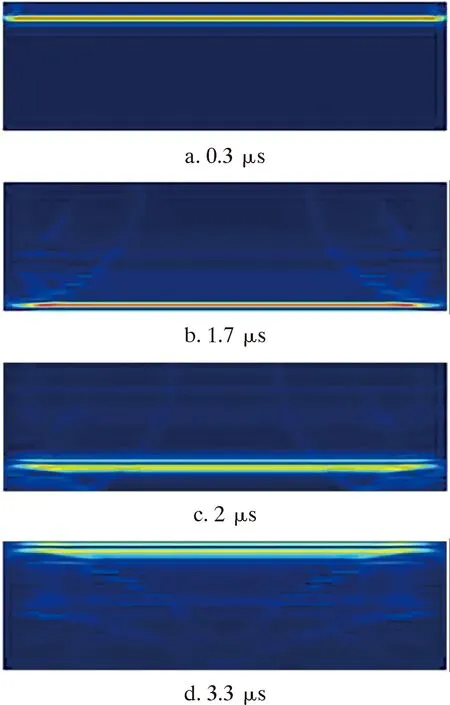
图17 超声波在完好管道工件中的传播示意图
图18是超声波在有内部缺陷的管道工件中的传播。在图18b中,当波到达裂纹处时,直接接触的部分由于空气声阻抗远大于钢材料,发生全反射;在1.6 μs时提前回到顶面,如图18c所示;剩余部分在3.3 μs时回到激励处,如图18d所示。
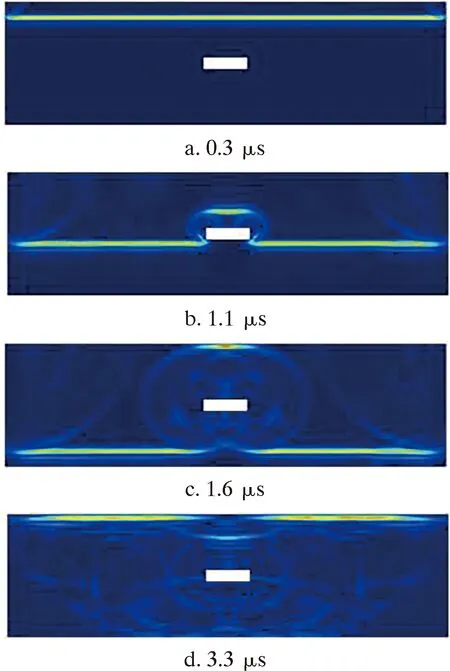
图18 超声波在存在内部缺陷的管道工件中的传播示意图
图19是超声波在存在表面腐蚀的管道工件中的传播示意图。由于受腐蚀的管道部分厚度较完好管道小,超声波传播的距离变短,所以超声波在1.3 μs便到达底面,如图19b所示。超声波会在2.3 μs回到激励处,比正常情况下少1 μs,如图19d所示。

图19 超声波在存在表面腐蚀的管道工件中的传播示意图
5 结 论
(1)设计的管道机器人采用有源驱动模块,可在输油管道内独立运行。额定运动速度为5 cm/s,最大测试运动距离为1 km,最小过弯半径为813 mm。
(2)驱动模块创新使用了同步带,大大增强了越障能力及运动的稳定性。
(3)在管道机器人变径模块的设计上改进了传统的升降式变径机构,使其变径范围可达到114~325 mm。
(4)根据超声波检测理论,该管道机器人可以通过超声波探头与耦合喷头相互配合的方式对输油管道管壁进行检测。通过仿真与计算,探头理想探测范围占管道内壁面积的84%。
