高压管汇活动弯头接触特性分析*

2022-02-13张国友

石油机械 2022年12期

张国友

(中石化四机石油机械有限公司)

0 引言

压裂技术在油气田中使用日益广泛[1]，在非常规油气开发中[2]，通常需要面对复杂的井身结构、复杂的岩性和复杂的流体性质，这对压裂设备提出了更高的要求，需要有良好的耐高压、抗腐蚀、耐冲蚀特性。但是目前高压管汇在实际工作中的寿命远远短于其他的压裂设备，严重制约了油气田整体开发效益，所以需要对高压管汇易损件进行研究[3-7]。

为了延长活动弯头的使用寿命，许多学者进行了大量研究并取得了一定进展。徐晓东等[8]通过对活动弯头结构和加工工艺改进来延长活动弯头使用寿命。敬佳佳等[9]利用CFD软件分析放喷管角度、位置、放喷量、含砂率、颗粒形状对壁面冲蚀率的影响，指出含砂率对最大冲蚀率的影响较大，弯管位置对最大冲蚀率的影响较小，放喷管最大冲蚀率随含砂率、颗粒形状系数的增大而增大，随弯管角度和直管段长度增大而减小，随着放喷量的增加最大冲蚀率先增大后减小。郭登明等[10]针对现有活动弯头出现明显压痕和点蚀的情况，以20CrNiMo活动弯头为研究对象，将活动弯头进行渗碳+等温淬火+回火热处理，观察活动弯头金相组织的变化，发现工件表面为下贝氏体金相组织，该组织具有良好的耐磨性和抗腐蚀性，内部为下贝氏体和马氏体的混合金相组织，该组织可以有效防止裂纹扩散。

以上研究多以弯头加工工艺、弯头最大冲蚀率、弯头热处理工艺为主，对大通径四滚道活动弯头接触特性规律研究有待完善。笔者以大通径四滚道活动弯头为研究对象，采用增广拉格朗日乘子法[11]，分析不同滚道轴向间距、径向间距、滚道半径对活动弯头最大接触应力的影响规律。笔者对滚道接触应力进行分析总结，以期为活动弯头的设计、优化提供指导。

1 有限元接触算法

1.1 罚函数法

罚函数法相当于在接触面与目标面之间引入弹簧系统。在未接触时，弹簧系统不发生作用；在接触发生时，弹簧系统就会阻止接触物体相互嵌入[12]。为方便系统计算，在不含接触总位能基础上引入一个惩罚势能：

(1)

式中：ΠP(U)为惩罚势能，J；EP为惩罚因子，N/m；P为嵌入深度，m；U为节点位移，m。

这样，接触问题就等价于无约束优化问题：

minΠ*(U)=Π(U)+ΠP(U)

(2)

式中：Π*(U)为接触总位能，J；Π(U)为不含接触总位能，J。

罚函数法受接触刚度的影响较大。接触刚度越大，穿透量越小；接触刚度越小，穿透量就越大。理论上而言，当我们将接触刚度设定到无穷大时，其穿透量即可以为0，但是刚度矩阵不可能无穷大，否则刚度矩阵呈现病态。

1.2 拉格朗日乘子法

拉格朗日乘子法[13]是通过类比拉格朗日法的数学意义，以g(x)为约束条件，f(x)作为目标函数，引入拉格朗日乘子λ来构造公式：

L(x)=f(x)+λg(x)

(3)

在接触非线性问题上，拉格朗日乘子法以接触力的拉格朗日乘子λ乘以无侵彻条件，构造接触约束条件的附加泛函：

ΠC(U，λ)=λg

(4)

式中：ΠC(U，λ)为含接触约束条件的附加泛函，J；λ为拉格朗日乘子；g为接触约束条件。

最终将约束条件极值问题转化为无条件极值问题：

minΠ*(U，λ)=Π(U)+ΠC(U，λ)

(5)

拉格朗日法不再通过定义刚度来计算接触力，而是将接触力作为一个自由度，扩大了刚度矩阵。该算法优点是精度高；缺点是失去系数矩阵正定性，不易收敛。

1.3 增广拉格朗日乘子法

在增广拉格朗日乘子法[14]下，系统的总位能由不含接触约束条件的总位能Π(U)和惩罚势能ΠP(U)以及含接触约束条件的附加泛函ΠC构成，构造修正的势能泛函如下：

Π*=Π(U)+ΠP(U)+ΠC(U，λ)

(6)

增广拉格朗日是先将程序按照罚函数法进行开始计算，通过赋予允许穿透的最大值。如果在计算迭代过程中出现穿透量大于许用穿透量，则对刚度矩阵进行更新，将各个接触单元的接触刚度加上接触力乘以拉格朗日乘子的数值，形成不断更新刚度矩阵的罚函数法，也就是拉格朗日法。随着刚度矩阵的不断更新，最终穿透量将小于允许值，计算则停止。极大地克服了罚函数法的病态矩阵，以及拉格朗日法的刚度矩阵零对角元问题。

2 活动弯头有限元接触分析

2.1 物理模型及网格划分

本文选取某厂型号为ø130.2 mm-105 MPa(5in-15 000 psi)的大通径活动弯头为研究对象，采用Solidworks对其进行三维建模。该活动弯头为四滚道活动弯头，4个滚道安装钢球数量分别为32、33、34和35颗，其中第一滚道钢球数量为32颗。因为活动弯头活动节整体结构比较复杂，无法对其直接进行接触分析。查阅文献可知，活动弯头第一滚道接触应力较大，所以模型以第一滚道32颗钢球为参考，建立活动弯头活动节1/32分析模型，如图1所示。

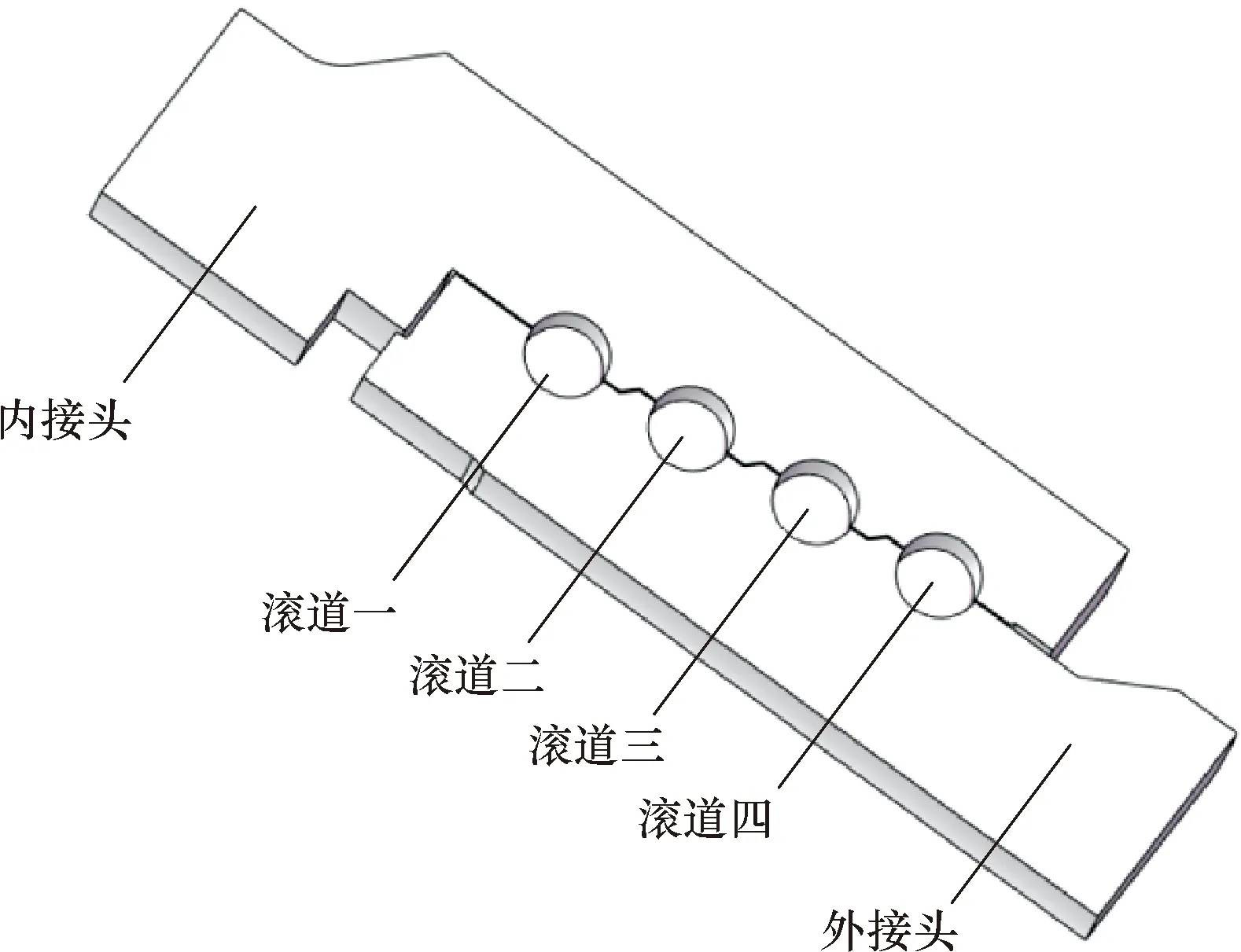
图1 活动弯头简化模型示意图

在活动弯头使用期间，活动弯头滚道表面容易出现压痕和点蚀。其中第一滚道最严重。因此，需要对活动弯头进行弹塑性接触分析，其中在活动弯头活动节塑性阶段采用双线性模型。材料的密度ρ=7 850 kg/m3，弹性模量E=210 GPa，泊松比υ=0.275，屈服强度σs=896 MPa，切线模量Etan=21 GPa。

考虑到弹塑性接触分析对网格要求较高，本文采用如下网格划分方式：首先对球体进行切分，切分后可以自动生成规则的六面体网格；为保证滚道网格基本与钢球网格一致，采用球体加密网格方式，以钢球球心为坐标原点，对滚道一圈进行网格加密。对于非接触区域不存在塑性变形，顺延滚道六面体划分方式。网格大小设置为5 mm，划分结果如图2所示。

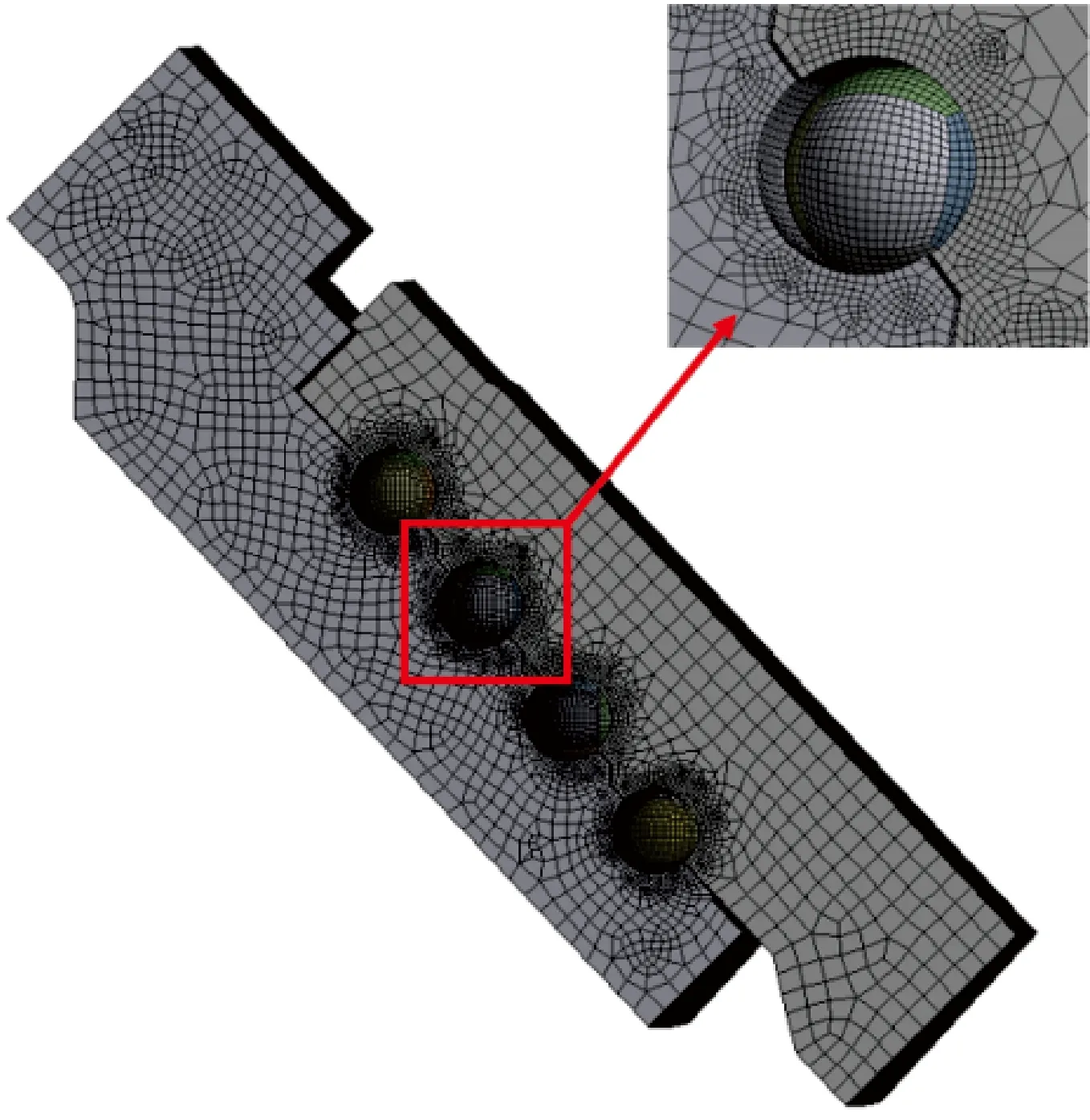
图2 活动弯头网格划分

2.2 边界条件

根据活动弯头的实际工况，对活动弯头有限元网格模型施加载荷和边界条件。活动弯头主要承受2种载荷：内压和轴向载荷。内压作用在外接头和内接头内壁面，外接头在管壁内压作用下产生径向位移，钢球在外接头和内接头共同作用下产生挤压变形；轴向载荷是在管内流体压力作用下，将管道看作密闭容器，外接头和内接头都将受到管内流体对管道的横向作用力。在施加载荷时，根据施加工况直接在外接头和内接头管道内表面施加内压105 MPa的压力；轴向载荷可以在内接头端面施加，外接头端面采用位移约束，约束外接头端面轴向位移。内接头端面载荷采用均布载荷方式施加，均布载荷p可以通过下式求得：

(7)

式中：po为管壁内压，MPa；Si为内接头外端面内圆的面积，mm2；So为内接头外端面外圆的面积，mm2；di为内接头外端面的内径，mm；do为内接头外端面的外径，mm。

活动弯头钢球多，钢球与滚道接触较多，不利于分析。上文对模型进行简化，取1/32进行分析，所以对外接头和内接头侧面需要进行合理约束，本文采用法向无位移约束。施加载荷和边界条件后的模型如图3所示。

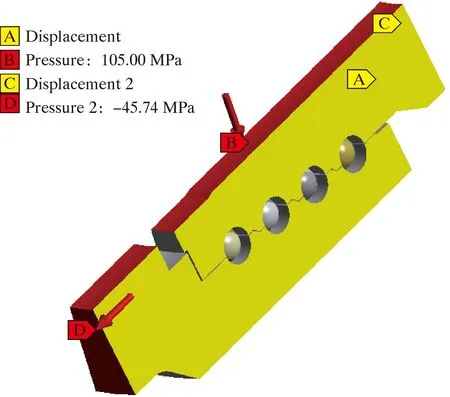
图3 边界条件和载荷施加图

2.3 网格无关性验证

通过对数值模型的试算，钢球的法向接触刚度因子与网格数量对弹塑性接触非线性仿真分析结果有较大影响，为确保计算结果的正确性，进行无关性验证。首先计算最大接触应力与网格大小的关系，计算结果如图4所示。

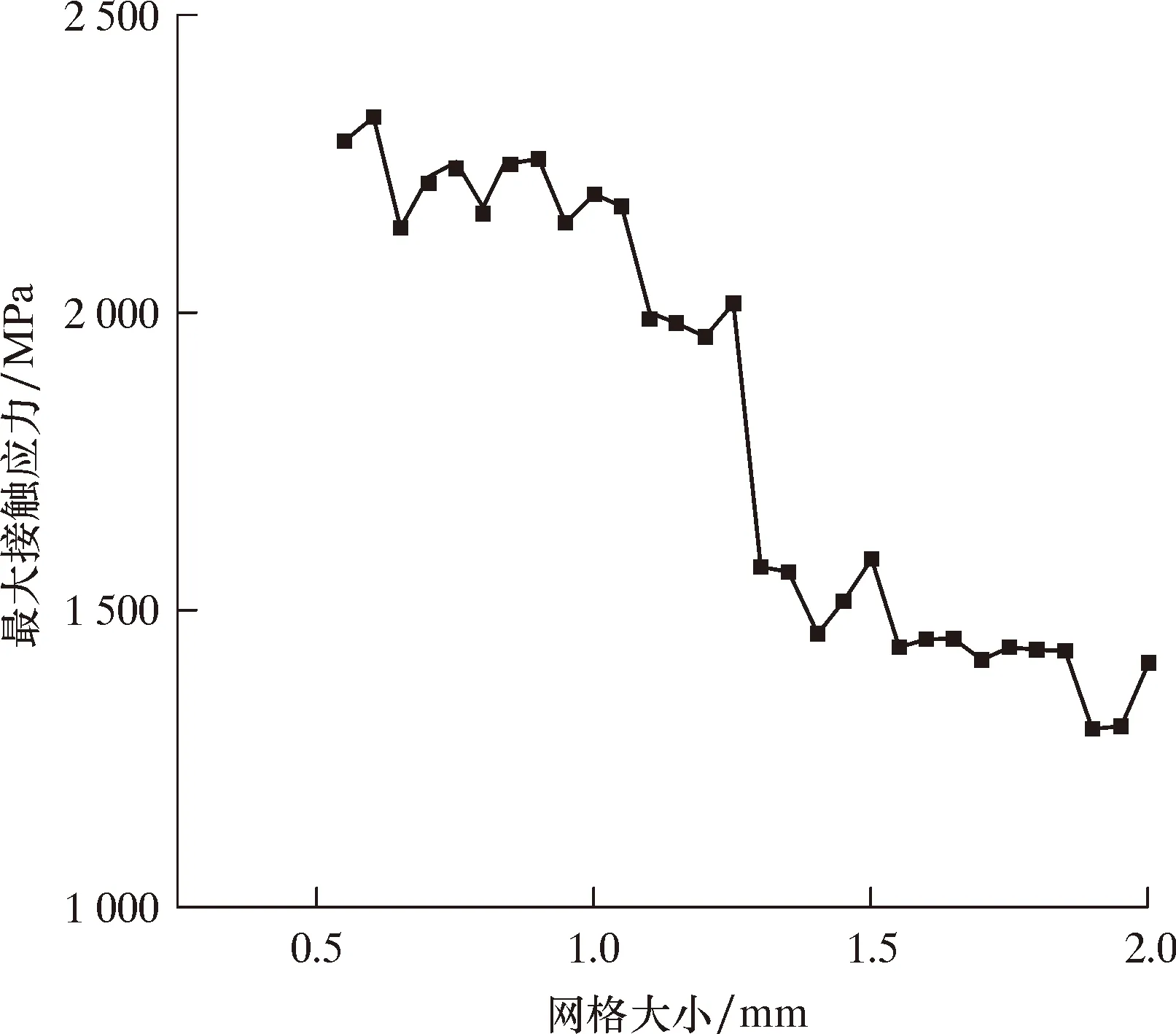
图4 最大接触应力与网格大小关系图

通过对网格无关性验证可以得到，随着网格不断减小，网格量不断增大，结果趋于收敛。网格尺寸在0.65～1.05 mm时接触应力波动较为平稳，分布较为均匀。若将网格继续加密，接触应力开始出现不规则，分布不均，开叉等不正常现象。网格尺寸在0.65～1.05 mm范围内的最大接触应力为2 264.5 MPa，最小接触应力为2 145.2 MPa，误差为5.26%，精度满足要求。综合上述分析，本文选取网格大小为1.05 mm，在此基础上选择合适的法向接触刚度因子，计算最大穿透量、最大接触应力与接触面法向接触刚度因子的影响，如图5所示。

图5 最大接触应力、最大穿透量与接触刚度因子关系图

查阅文献可知[15]法向刚度控制接触面和目标面之间的穿透量。较高的法向刚度会降低贯入量，但会导致整体刚度矩阵的病态和收敛困难。较低的法向刚度可能导致一定数量的穿透，并产生不准确的解决方案。理想情况下，需要一个足够大的法向刚度，使渗透足够小。通过对不同法向刚度分析计算，可以看出随着接触面法向刚度的增加，接触面与目标面的最大穿透量不断减少趋于收敛；最大接触应力逐渐增大直至稳定，综合考虑，选取法向接触刚度因子为10。

2.4 仿真计算结果

采用Workbench软件对活动弯头进行弹塑性接触非线性分析，得到滚道接触应力如图6和图7所示。由图6和图7可知，接触应力云图呈现椭圆形，与赫兹理论假设一致，分析结果合理。外接头和内接头第一滚道接触应力都明显大于其余滚道，呈现逐渐减小趋势，与现场第一滚道压痕最为严重的现象一致。对比外接头与内接头滚道最大接触应力可以发现，外接头滚道最大接触应力比内接头大。

图6 外接头滚道接触应力云图

图7 内接头滚道接触应力云图

图8为活动弯头结构示意图。本文将结构划分为6个区域。由上文可知，活动弯头所受载荷主要有2种。活动弯头内壁在承受载荷时，活动弯头所有区域在径向上都会外扩，区域1壁厚较大，在区域5共同作用下，不易变形；区域4壁厚较大，在区域6共同作用下，不易变形；相较于区域1、区域4，区域2、区域3径向变形较为容易。在内压作用下，区域3推动区域1，区域4推动区域2，区域3可以过滤内压能量不如区域4，剩余能量都由区域1承担；区域4过滤较多的内压能量，剩余的能量到区域2，又因为区域2径向易变形，而区域1不易变形，所以造成滚道严重偏载。活动弯头在承受轴向载荷时，所有区域在径向上都会有远离钢球的趋势，在第一滚道和第二滚道都有径向易变形区和不易变形区，所以轴向载荷并不是造成滚道偏载的主要原因。

图8 活动弯头结构示意图

以外接头滚道最大接触应力为判定依据，通过对活动弯头内压和轴向载荷单独分析,再与载荷共同作用进行对比，得出不同载荷下滚道所受最大接触应力，分析结果如表1所示。

表1 不同载荷工况下滚道最大接触应力

由表1可以看出，在轴向载荷单独作用下，滚道最大接触应力相差不大；在管壁内压单独作用下，第一滚道相对第四滚道最大接触应力降低了44.68%；在轴向载荷和管壁内压共同作用下，最大接触应力降低了31.70%。由此可见，轴向载荷对管壁内压导致的滚道接触应力偏载有一定的缓解作用。

3 活动弯头接触应力影响因素分析

由上述仿真可知，活动弯头存在接触应力过大和偏载现象，笔者对接触应力偏载做出了解释，并在此基础上分析活动弯头结构参数对滚道接触应力的影响。弯头结构参数主要包括滚道轴向间距、滚道径向间距和滚道半径。

3.1 滚道轴向间距

在滚道结构参数不变的情况下，选取不同大小的滚道轴向间距分别为27.4、31.4、35.4、39.4和43.4 mm。研究滚道轴向间距对活动弯头滚道接触应力的影响规律，整理数值仿真数据可得活动弯头滚道最大接触应力随滚道轴向间距的变化规律，如图9所示。

图9表明，随着活动弯头滚道轴向间距的增大，第一滚道、第二滚道最大接触应力呈现上升趋势，第三滚道最大接触应力上下波动，第四滚道最大接触应力呈现下降趋势。因为随着滚道轴向间距的增大，外接头内壁面承载内压面积增大，单个钢球所需承载的载荷增加，但是区域3过滤内压能力没有区域4强，所以导致活动弯头滚道最大接触应力的增加。

图9 不同滚道轴向间距下的最大接触应力

3.2 滚道径向间距

在滚道结构参数不变的情况下，选取不同大小的滚道径向间距分别为0、1.1、2.1、3.1、4.1、5.1和6.1 mm。研究滚道径向间距对活动弯头滚道接触应力的影响规律，整理数值仿真数据可得活动弯头滚道最大接触应力随滚道径向间距的变化规律，如图10所示。

图10 不同滚道径向间距下的最大接触应

图10表明，随着活动弯头滚道径向间距的增大，第一滚道、第二滚道最大接触应力呈现上升趋势，第三滚道最大接触应力上下波动，第四滚道最大接触应力呈现下降趋势。这是因为随着弯头滚道径向距离变大，区域1和区域4的壁厚变大，区域2和区域3的壁厚没有改变，导致区域4承载的内压比例增加，分配给区域2的内压能减少；区域3承载的内压比例基本不变，但是区域1壁厚增加，导致结构刚度增加，更加不易发生形变，致使钢球形变增大，所以接触应力增大。