Mathematica在基础工程学教学改革中的应用★

吴雪婷，陈 斌

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.杭州师范大学理学院，浙江 杭州 311121)

1 概述

基础是建筑结构的重要组成部分，它承受着建(构)筑的全部荷载并将荷载传递给地基，合理选择地基基础的设计方案对建筑物的安全使用和工程造价至关重要。在进行地基基础设计时，大量的科研、工程技术人员结合理论和工程实际，归纳总结出了诸如查表法、经验系数法、简化模型法、试算法等传统方法，在工程建设中发挥了巨大的作用。

基础工程学是土木工程类专业的一门主干必修课程。面对传统教学中烦琐的计算过程和复杂的方程求解，学生的注意力往往放在具体的计算步骤上，而忽视了对建模和计算方法的本质理解。因此，从教学的角度看，教师的重要任务是让学生知其然，并知其所以然。很多一线教师从教学观念、教学思路、教学方式、教学实践[1-3]等各个环节开展了适应现代化发展和新工科教育理念的教学改革。

随着计算机技术的发展，工程设计方法也不断更新，Mathematica是一款符号计算软件，拥有强大的数值计算和符号运算能力，广泛使用于科学、工程、数学、计算等领域。目前，Mathematica已用于数学[4]、物理[5]、航空[6]、土木工程[7]等领域的课程教学中，并取得了一些成效。利用Mathematica辅助教学有利于增强教学内容的直观性，激发学生的学习兴趣，加深对理论知识的理解，拓展数值分析的能力；同时可以将学生从繁杂的计算中解脱出来，从而关注问题的实质。

基于此，本文以浅基础的基础底面尺寸计算的不确定性问题为例，将Mathematica编程引入到基础工程学的教学改革中。首先将传统试算法与Mathematica辅助编程法进行对比，帮助学生理解计算结果的物理和工程意义；再利用Mathematica软件绘图，探讨解析法中如何形象直观地求解一元三次方程和不等式的问题，从而更方便快捷地得到基底尺寸。

2 计算基础底面尺寸的不确定性问题

在基础工程学中，对于天然地基上的浅基础，在初步选择基础类型和埋置深度后，就可以计算地基持力层的承载力特征值和作用在基础底面的荷载值，进行基础底面尺寸设计[8]。例如在轴心荷载作用下，按地基持力层承载力计算基底尺寸时，基础底面积的计算公式如下：

(1)

其中，A为基础底面面积，A=bl，b为基底短边边长，l为基底长边边长；Fk为相应于作用的标准组合时，上部结构传至基础顶面的竖向力值；fa为修正后的地基持力层承载力特征值；γG为基础及回填土的平均重度；d为基础平均埋深；γw为水的重度；hw为地下水位至基础底面的距离。

通常轴心荷载作用下，采用方形基础(即A=b2)，则基础边长b为：

(2)

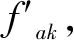
fa=fak+ηbγ(b-3)+ηdγm(d-0.5)

(3)

其中，fa为修正后的地基承载力特征值；fak为地基承载力特征值；ηb,ηd分别为基础宽度和埋深的地基承载力修正系数，可按基底以下土的类别查规范[9]表格得到；γ为基础底面以下土的重度；b为基础底面宽度，当基底宽度小于3 m时按3 m取值，大于6 m时按6 m取值；γm为基础底面以上土的加权平均重度；d为基础埋置深度。

由式(3)可知，在对fak进行修正时，是需要知道b值的，但由于基底宽度b是未知待求的参数，因此，只能采取假设法。首先假设b≤3 m，则式(3)中的ηbγ(b-3)=0，此时仅对fak进行埋深d的修正，将得到的fa代入式(2)计算可得b。再比较计算得到的b和假设的b≤3 m是否一致。如果一致，则计算值即为所求的基底尺寸；如果计算得到的b>3 m与假设不一致，则在计算基础尺寸之前需要对fak同时进行d和b的修正，这时式(3)中的ηbγ(b-3)≠0，需要迭代试算才可得到基底尺寸。

因此，在计算基础底面尺寸时出现了上述不确定性问题，传统教学的求解方法是假设试算法，该方法容易导致学生对上述计算步骤理解不透彻，对计算结果的工程意义一知半解。

3 基于Mathematica的基底宽度求解

针对上述问题，本文将Mathematica程序引入基础工程学的教学，利用Mathematica对基底宽度b进行了编程求解，分析了不同地基土层条件下(淤泥、黏土和中砂地基)，基础底面宽度与基础顶面荷载的关系，讨论了上述不确定性问题的解。

以基础工程学的某教材例题为算例[10]，某黏性土重度γm为18.2 kN/m3，孔隙比e=0.7，液性指数IL=0.75，地基承载力特征值fak为220 kPa。现修建一外柱基础，作用在基础顶面的轴心荷载Fk=830 kN，基础埋深(自室外地面起算)为1.0 m，室内地面高出室外地面0.3 m，需要确定方形基础底面宽度b。

传统的计算方法和步骤为：首先假设b≤3 m，先进行地基承载力的深度修正，查规范表格可知黏土的ηd=1.6，再利用式(3)得到fa=235 kPa；最后利用式(2)得到b≥1.98 m，取b=2 m；由于b=2≤3，与假设一致，所以不必进行承载力宽度修正。传统的求解方法只能首先假设b值和3的大小关系，再根据已知的参数查表和计算，每次计算只能得到一个确定的b值。如果计算的b值与假设不一致，则需要代入公式，反复试算。

分析式(2)和式(3)可知，当基底宽度b≤3 m时，对于某一类别的地基土层而言，基底宽度b的大小仅与Fk有关：Fk越大，则基底宽度b越大。利用Mathematica软件编程，可以绘制基底宽度b随荷载Fk的变化曲线，如图1中的实曲线所示。当0≤Fk≤1 900 kN时，恒有基底宽度b≤3 m，不会出现与假设不一致需要反复试算的问题；而当Fk>1 900 kN时，基底宽度才会有b>3 m，出现与假设不一致的问题，此时图1中的实曲线在b>3 m段需要重新代入式(3)进行修正，并重新按照式(2)计算。重新计算和反复试算的过程也可通过Mathematica软件编程来求解，可得图1中所示的虚线曲线段。由图1中的实线和虚线在3 m≤b≤6 m的对比可知，对于任意荷载Fk值，虚线的纵坐标恒小于实线的纵坐标，即再次计算的基底宽度b恒小于第一次的计算值，且对于该类黏土地基而言，第二次计算值仍然满足b>3 m，即可得到正确的基底宽度b值。

实现图1中数据计算及曲线绘制的Mathematica程序的部分主要源代码如下：

niantuyy1=Plot[Sqrt[(Fk/(fakNiantu+ηdNiantu*γmNiantu*(d1-0.5)-γG*d2))*p/n],{Fk,0,50000}, PlotRange->{{0,8000},{0,7}}, AspectRatio->1];

niantuyy2=Plot[Sqrt[(Fk/(fakNiantu+ηbNiantu*γ*(Sqrt[(Fk/(fakNiantu+ηdNiantu*γmNiantu*(d1-0.5)-γG*d2))*p/n]-3)+ηdNiantu*γmNiantu*(d1-0.5)-γG*d2))*p/n],{Fk,1900,8000},PlotRange-> {{0,50000},{0,7}}, PlotStyle->{Red, Dashed}, AspectRatio->1]

通过Mathematica软件编程求解和绘制曲线，模拟了黏土地基上基底宽度b与荷载Fk的关系。Mathematica程序代码编写简单，计算速度快，直观形象地解决了此工程设计计算中关于基底尺寸的不确定性问题。而且，只需改变上述程序源代码中的参数，就可以方便快捷地得到其他类型地基土层的相关关系曲线，如图2所示(图2中曲线1代表淤泥地基，曲线2代表黏土地基，曲线3代表中砂地基)。根据图2可以对不同类型地基土层上的基础底面尺寸进行对比分析，当3 m≤b≤6 m时，对于淤泥地基，实线和虚线重合；对于中砂和黏土地基，遵循相同的规律，但中砂地基第二次计算值与第一次计算值的偏差大于黏土地基。

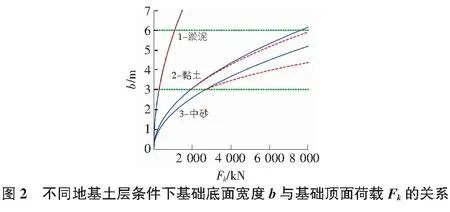
上述编程求解过程和曲线模拟通过Mathematica软件可以很方便地实现，如果采用传统手算、查表的试算法，不仅计算难度大、计算过程复杂，也很难得到上述结果和规律。

4 Mathematica图像分析在基底尺寸的解析法中的应用

除了一般教材中对于基础底面尺寸的传统试算法，以及本文基于Mathematica的求解法以外，还有直接计算的解析法[11-12]。解析法的思路是将式(3)代入式(2)中，可得：

(4)

再将式(4)化简，可得到一个关于b的一元三次不等式：

α3b3+α2b2+α0≥0

(5)

式中：

α3=ηbγ

(6)

α2=fak-3ηbγ+ηdγmd-0.5ηdγm-γGd+γwhw

(7)

α0=-Fk

(8)

由式(5)可知，求轴心荷载作用下的基础宽度b本质上是一元三次不等式的求解问题，可按Cardan公式法求解。为了得到定量的解，需要求解一元三次方程，这个过程是复杂和困难的。但是借助Mathematica的绘图功能，可以很方便地得到y与b的函数关系曲线，便于直接读图判断。

本文利用Mathematica软件编程，绘制函数y=f(b)=α3b3+α2b2+α0的曲线。根据工程实际意义，y≥0，b恒大于0，则该曲线与横轴坐标轴正值的交点即为所求的基础宽度b。仍以上述例题为例，编程计算并绘制轴心荷载Fk=830 kN,Fk=1 900 kN和Fk=3 000 kN时，函数y=f(b)的曲线如图3所示，从图3中可直观地得到对应的b=2 m,b=3 m和b=3.7 m。由此可见，利用Mathematica软件辅助计算和绘图，可以方便快捷、直观形象地得到基础宽度b，从而简化了解析求解法中求解一元三次方程和不等式的复杂过程。

5 结论

利用Mathematica编程，可以直接计算并绘制基础底面宽度与基础顶面荷载的关系曲线，不仅简化了反复试算的求解过程，而且解答了传统手算法所不能计算的不确定性问题。此外，基于Mathematica编程绘图功能，也简化了解析算法中一元三次方程和不等式的求解过程。

基于Mathematica的求解在基底宽度b的传统试算法和解析算法中均得到了很好的应用，一方面提高了学生的学习兴趣和积极性，加深了学生对基础工程学知识的理解，帮助学生更好地理解了基底尺寸求解过程中的假设-计算-重新假设-重新计算……的逻辑思路；另一方面，新教学法还锻炼了学生发现问题-分析问题-解决问题的能力，使学生将来能更好地利用现代化手段解决工程实际问题。