大跨度跨海铁路连续刚构桥波浪荷载动力响应研究

罗浩 甘贤备 晏亮 吕海龙 杨彤麟 郭辉

1.湖南科技大学土木工程学院，湖南 湘潭 411201；2.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081

跨海桥梁结构承受随时间和空间变化的各种随机荷载，如风荷载、波浪荷载等。大多数研究只考虑风荷载作用在桥梁上的一些动力特性，而忽略了波浪荷载的影响［1-4］。波浪荷载对桥梁的作用是一个复杂的非线性流固耦合问题，难以有效模拟波浪荷载。根据海洋工程波浪理论，海洋工程结构分为小尺度结构物和大尺度结构物。对于小尺度结构物，采用Morison等［5］提出的莫里森方程计算波浪荷载。对于跨海大桥的桥墩、桥塔或承台结构，当特征尺寸与入射波波长比值大于0.2时，其对波浪场的影响不可忽略，应按大尺度结构物来计算波浪荷载。在实际工程中，基于绕射理论或Froude⁃Kylov理论的求解方法，即使仅求解一阶问题，能得到解析解的结构也非常少。因此，大量结构物的波浪荷载求解采用数值方法［6］。随着数值求解技术的高速发展，很多学者对计算流体动力学（Computational Fluid Dynamics，CFD）波浪数值水槽进行了深入研究，并取得了很多的研究成果［7-9］。

本文基于计算流体力学及波浪力学理论，运用CFD软件对波浪场进行数值模拟，研究大跨度连续刚构桥在波浪荷载作用下的动力响应规律。

1 CFD造波理论基础

1.1 基本控制方程

质量守恒方程（连续性方程）［10-12］为

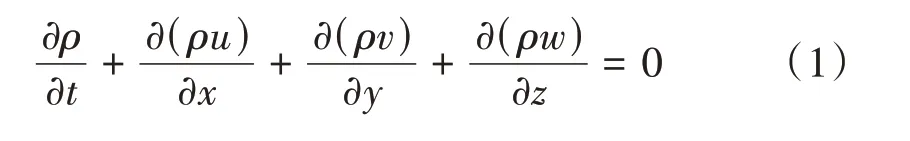
式中：ρ为流体密度；t为时间；u、v、w分别为流体运动速度在x、y、z三个方向的分量。

动量守恒方程（Navier⁃Stokes方程）［10-12］为

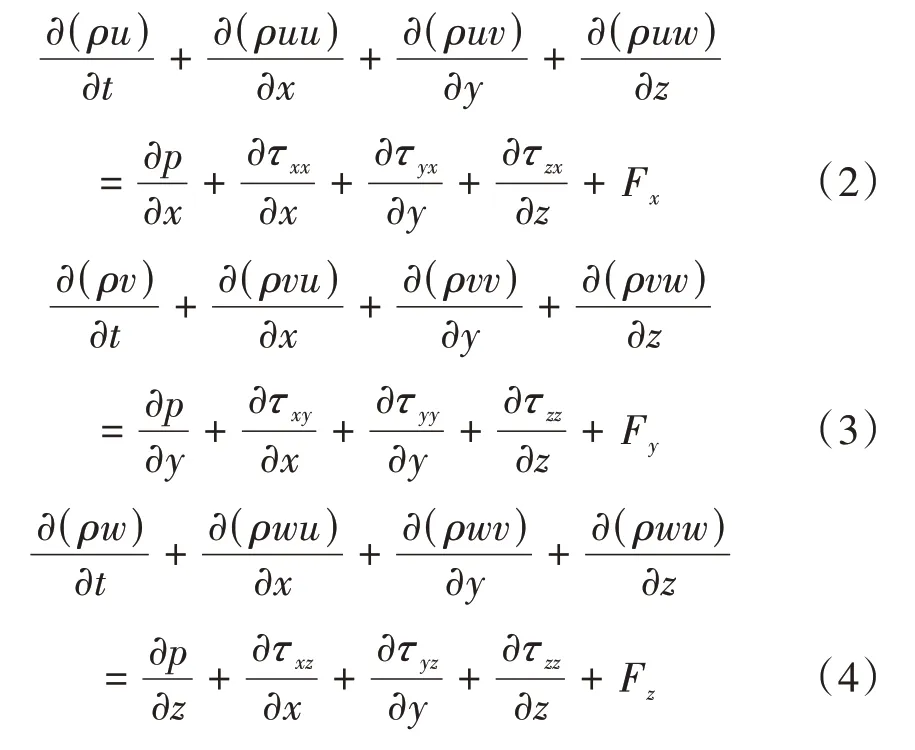
式中：p为流体微元体上的压力；τxx、τxy、τxz均为黏性应力分量；μ为动力黏性系数；Fx、F y、Fz均为体积力。

1.2 湍流控制方程

波浪运动属于经典的湍流运动。湍流数值模拟的方法分为两类：直接数值模拟方法和非直接模拟方法。由于直接数值模拟方法求解三维问题对计算机内存空间及运算速度要求很高，目前还无法真正用于工程上的计算。因此，一般选用非直接数值模拟方法。本文选择应用较广泛的Reynolds平均法（Reyn⁃olds Averaged Navier⁃Stoke，RANS）对湍流运动进行数值模拟。

能够体现湍流特点的湍流模型有标准k⁃ε模型和RNGk⁃ε模型，k为风湍动能，ε为湍流耗散率。标准k⁃ε模型假定湍动黏度是各向同性的，对低雷诺数、大曲率强旋流的流动适用性较差；RNGk⁃ε模型对湍流黏度比进行修正，并充分考虑流体在旋转中、旋流流动的影响，更好地解决了高应变率和流线设计中弯曲程度较大的流动。由于大跨度连续刚构桥和三维波浪场相互作用，波浪荷载会出现变形破碎，因此本文湍流模型采用RNGk⁃ε模型［10］，即

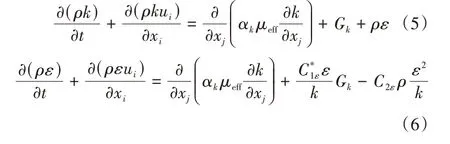
式中：ui为时均速率；αk为逆有效普朗特数，αk=1.39；μeff为有效黏性系数，μeff=μ+μt，μt=ρCμk2/ε，Cμ=0.0845；Gk为时均速度梯度引起的湍动能产生项；C1ε-[η(1-η/η0)/(1+βη3)]，C1ε=1.42；η为平均流时间尺度与湍流时间尺度之比；η=(2E ij E ij)1/2k/ε；Eij为平均应变速率张量，E ij=(∂u i/∂x j+∂u j/∂x i)/2；η0=4.377，β=0.012；C2ε=1.68。

1.3 边界条件及初始条件

进口设置为速度入口边界，初始时刻的初始速度为0，水面为静水面。出口边界采用出流（Outflow）边界条件，即Sommerfeld辐射边界条件。

1.4 数值造波方法

本文主要通过设置水槽进口造波边界相关波浪参数进行边界法造波。采用ANSYS中FLUENT板块自带的Open channel wave BC，通过设置合理的边界条件生成三维弦函数波浪。

定义入射波的波浪形式H为

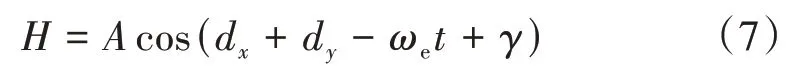
式中：A为振幅；γ为相位差；d为波数，d x=dcosθ，d y=dsinθ；ωe为有效波频率，ωe=ω+dU，ω为波频率，U为入射波速度。

2 CFD数值计算方法的验证

为了验证CFD数值计算方法的可行性，结构验证模型采用文献［8］的物理实验资料。波浪参数为：直径0.36 m，水深0.38 m，波高0.083 m，波浪周期1.35 s。根据试验模型参数，数值波浪水池的计算区域尺寸为8.0 m（长）×3.6 m（宽）×0.6 m（高），水槽宽度与筒径之比为4.44。数值模型见图1，波浪力时程曲线见图2。

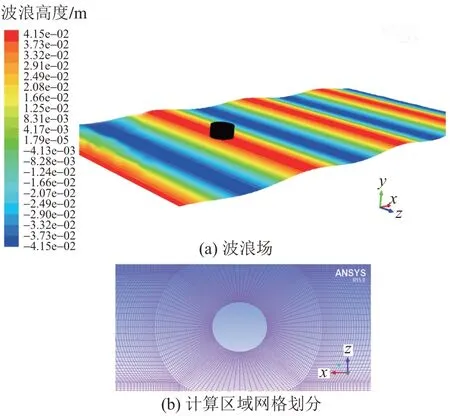
图1 数值模型

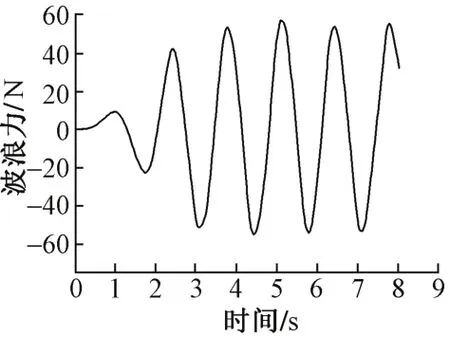
图2 波浪力时程曲线

由图2可知，本文模型波浪力计算峰值为57.0 N。文献［8］中单筒的波浪力峰值试验值和数值模拟值分别为56.5、54.6 N，本文模型计算值与文献［8］试验值接近，验证了本文采用的波浪场数值计算方法可行。

3 波浪荷载效应研究

3.1 工程概况

一座高速铁路跨海连续刚构桥（图3），跨度为（88+160+88）m，主梁采用单箱单室截面，跨中及端支座截面梁高为5.0 m，中支座处梁高为9.8 m；主墩为双肢薄壁结构，墩柱中心距为8 m。受潮流影响，计算采用历史最高水位，距承台底部13.4 m。

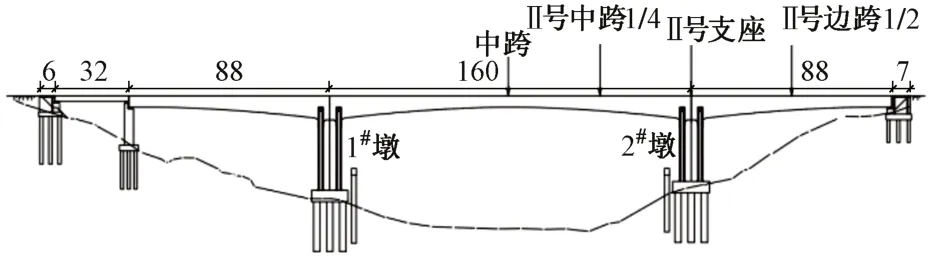
图3 连续刚构全桥立面（单位：m）

梁和墩采用beam188单元模拟，横隔板采用mass21单元模拟。建立模型时对结构施加如下约束：两端支座节点处约束竖向自由度和横向自由度，通过约束绕桥向的转动来实现；双肢薄壁墩与梁固结；墩底与承台简化为固结形式，通过约束墩底节点的所有自由度来实现。

3.2 CFD波浪荷载数值模拟

采用ANSYS软件中CFD模块建立波浪水槽模型，计算区域尺寸200 m（长）×80 m（宽）×32 m（高）。波浪传播方向网格节点距离选取渐进格式，桥墩附近局部加密到0.10 m，水面附近1倍波高内竖向网格节点距离取0.21 m，其余部分越远离水面的网格越稀。波浪沿x轴正向传播，波浪场速度云图见图4。

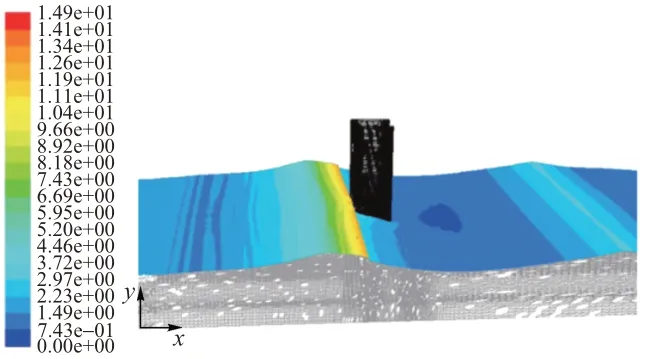
图4 波浪场速度云图（单位：mm·s-2）

3.3 CFD波浪荷载数值计算结果

3.3.1 相同周期下不同波高的桥梁动力响应

根据当地水文条件、波浪理论的基本规律和波浪力时程曲线随时间呈周期性变化的特点，绘制波高为2、3、4、5、6、8 m的波浪力极值变化曲线，见图5。

图5 不同波高下波浪力极值变化曲线

由图5可知，波浪力极值随波高的增大而增大，在波高为2～5 m时增幅较大，在波高为6～8 m时增幅较小。横桥向波浪力极值总是大于纵桥向波浪力极值，原因是波浪冲击桥墩时发生绕射，产生纵向波浪力，其值明显小于横桥向波浪力。

为了分析波高对连续刚构桥的影响，计算不同波高下波浪荷载作用在桥墩时的动力响应（波浪荷载周期为8.8 s、波长为90 m），见图6。可知：①跨中横向位移峰值总是大于支座和边跨横向位移峰值。随着波高的增大，跨中横向位移峰值与支座和边跨横向位移峰值的差值也随之变大，在波高为2 m时，差值分别为0.05、0.09 mm；在波高为8 m时，差值分别为0.20、0.28 mm。②各位置的横向位移峰值随波高增大而增大。③波高从2 m变化至5 m时峰值跨中位移增幅为190.0%；波高从5 m变化至8 m时峰值跨中位移增幅为9.6%。当波高增大到一定值时，跨中横向位移的增幅会减小。原因是本文中不同波高下波浪荷载周期均为8.8 s，当波高增大到一定值时结构的位移响应受波浪周期和波长共同影响。②峰值加速度整体变化规律与位移变化规律相似，当波高增大到一定值时，各位置加速度峰值的增幅会减小。

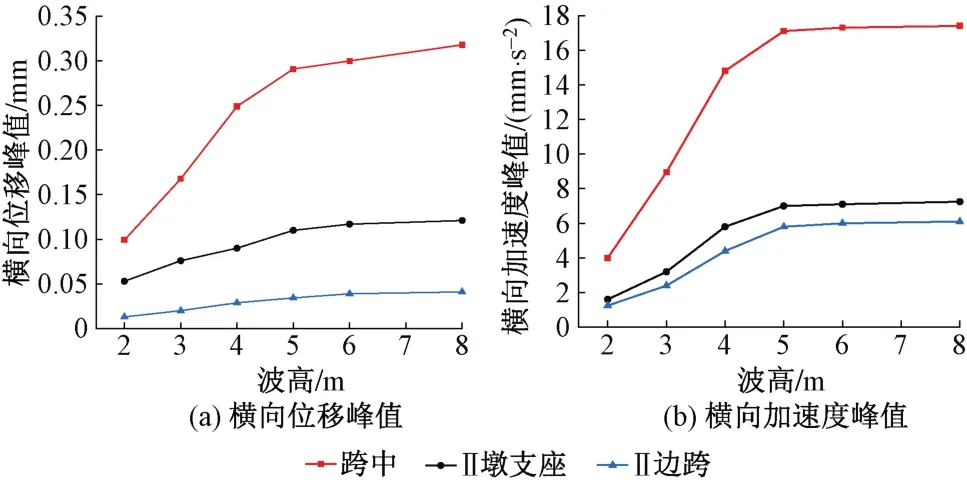
图6 不同波高下结构的动力响应

由于波高为5 m时结构的动力响应最大，为了解波浪荷载对刚构桥的动力响应规律，对比波高为2、5、8 m时跨中位移和加速度时程曲线，见图7。

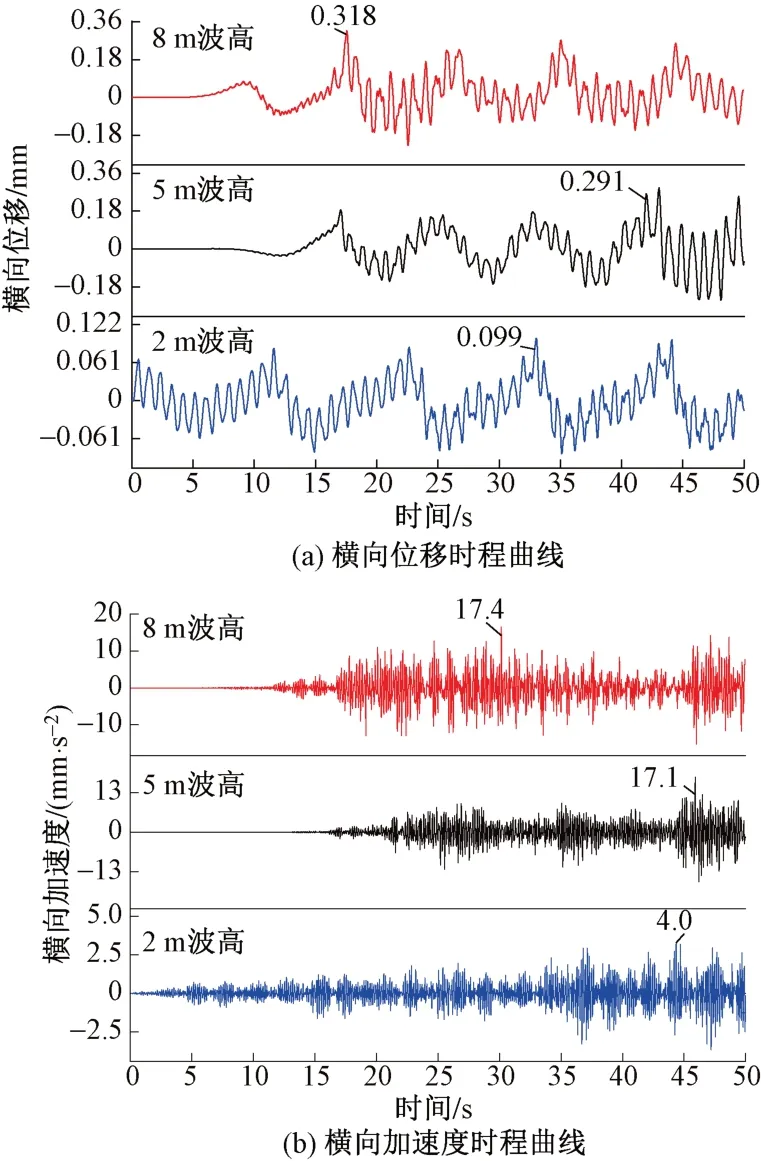
图7 不同波高下跨中横向位移和加速度时程曲线

由图7可知：①当波高为2、5、8 m的波浪荷载作用在连续刚构桥时，位移变化幅度分别为0.184、0.530、0.540 mm，跨中横向加速度峰值分别为4.0、17.1、17.4 mm/s2。②当波高较小的波浪荷载作用于桥梁时，加速度时程曲线和位移时程曲线在计算时间内持续变化；随着波高增大，位移和加速度产生较大的变化。③当波浪达到一定高度后，在波浪荷载作用的前一段时间内加速度和位移没有任何变化，存在滞后效应，且加速度和位移变化幅度相差不大。

不同波高下的跨中和墩顶横向位移峰值见图8。可知：①墩顶横向位移随波高增大而增大，当波高增大到一定值时，墩顶横向位移的增幅减小。②跨中位移峰值始终大于墩顶横向位移峰值，且随波高的增大二者差值逐渐增加。

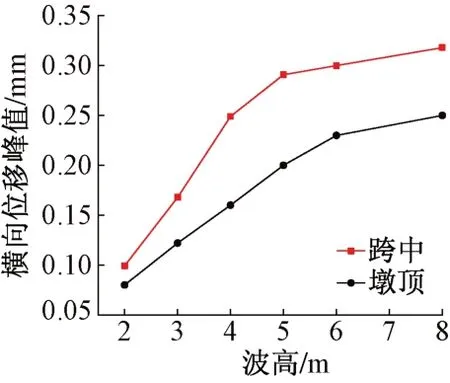
图8 跨中和墩顶横向位移峰值对比

3.3.2 相同波高下不同周期的桥梁动力响应

随着波高的增大，位移和加速度变化不明显的主要原因是波浪荷载周期相同。波浪的联合统计特征是：对于较大的波高，周期在平均周期附近比较集中；对于较小的波高，周期在平均周期附近比较分散。为了研究波浪周期对桥梁动力响应的影响，根据桥梁的实际场地情况，波高取2.4 m；结构对3～15 s的周期比较敏感，因此选取周期为3.3、3.5、4.0、5.0、5.8、6.4、8.0、10.0、12.0 s进行分析。不同周期下波浪力极值变化曲线见图9。

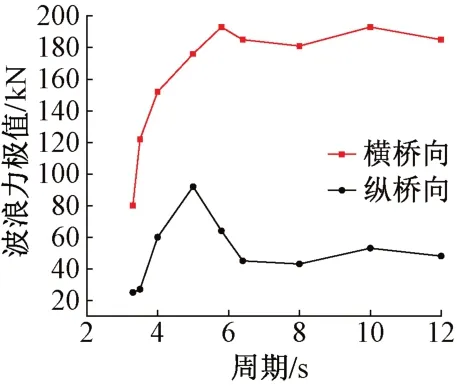
图9 不同周期下波浪力极值变化曲线

由图9可知：①周期为3.3～6.4 s时横桥向波浪力极值增长速率较大，周期大于6.4 s时变化幅度较小。②周期为3.3～5.0 s时纵桥向波浪力极值增长速率较大，周期大于5.0 s时，波浪力极值随周期的增加呈减小趋势。

选取2#墩附近采样点数据，对比不同周期下结构的动力响应，见图10。可知：①在波高相同的情况下，位移和加速度受波浪周期的影响较大。②不同位置位移响应和加速度峰值出现的周期为3.5～4.0 s。Ⅱ号边跨1/2、Ⅱ号支座处、Ⅱ号中跨1/4以及跨中的加速度峰值分别为0.088、0.780、0.850、1.190 mm/s2，位移峰值分别为0.007、0.011、0.021、0.031 mm。③随着周期的增加，位移和加速度逐渐减小；当周期增加到某一值时，位移和加速度的变化幅度减小，且趋于稳定。对比图6可知，在周期相同的情况下也有类似的规律。因此，对于此类刚构桥应合理考虑波浪周期和波高的影响，不能只考虑其中某一个因素。

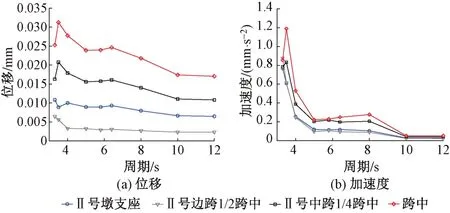
图10 不同周期下结构的动力响应

4 结论

1）跨中处位移总是大于桥梁其他位置的位移；跨中横向位移会随着波高增大而增大，但当波高增大到一定值时，跨中横向位移的增幅会减小；跨中横向加速度随波高的增大而增大，但波高增大到一定值时，跨中横向加速度的增幅不明显。

2）墩顶横向位移随波高增大而增大，但当波高增大到一定值时，墩顶横向位移的增幅会减小。

3）不同波高下跨中横向位移的峰值均大于墩顶横向位移的峰值。

4）对大跨度跨海桥梁进行波浪荷载动力研究时应合理考虑波浪周期和波高的影响，不能只考虑其中某一个因素。