悬臂支挡基坑开挖的离心模型试验研究
2022-02-12杨家新王耀王小华金红柳
杨家新 王耀,2 王小华 金红柳
1.北京城投地下空间开发建设有限公司,北京 100084;2.北京市基础设施投资有限公司,北京 100101;3.清华大学水沙科学与水利水电工程国家重点实验室,北京 100084
近年来,我国基坑工程事故频发,造成了重大人员伤亡和财产损失。为了建立安全的基坑支护体系,需要深入研究基坑的变形破坏特性。
基坑变形破坏的研究手段主要有现场观测、数值方法、模型试验等。现场观测结果作为基坑变形破坏的第一手实测数据,对于理解基坑变形破坏机理至关重要。已有许多学者结合施工过程中的监测数据及事故现场的灾害调查结果,总结了基坑变形破坏的形态和影响因素[1-3]。实际基坑工程干扰因素复杂且无法主动改变各类影响因素,在基坑变形破坏机理的研究中存在较大的局限。有限元等数值方法可以通过选择合适的本构模型对基坑中土与结构的相互作用进行合理模拟,且方便改变土性、施工条件等各类影响因素[4-6]。有限元计算的精度对土体本构模型和参数的选取依赖性较强,对于基坑破坏阶段的计算精度也有待进一步提高。
土工离心模型试验因具有模型和原型自重应力场相等、变形相似、破坏机理相同等优势,在基坑变形破坏研究方面得到了广泛应用[7-9]。基坑开挖离心模型试验方法的技术关键是如何合理模拟离心场中的开挖。目前的模拟方法主要有停机开挖和离心场开挖两类。停机开挖操作简单,是在1g重力场下进行开挖,再重新置于离心场中试验,模型应力路径与原型开挖应力路径明显不同;而离心场开挖能模拟与实际基坑工程相符的应力路径,合理模拟基坑的变形破坏过程[10-14]。文献[15]自主研发了一种离心场基坑开挖设备,采用加载单元模拟待开挖土体,能再现开挖前原型地基侧限状态的变形场和应力场,从而合理模拟开挖过程。目前,基坑离心模型试验的研究多集中在观察基坑开挖后的稳定性和变形破坏特性,对开挖条件下基坑变形过程、支挡结构土压力变化规律等的研究较少。
本文采用可实时模拟开挖的离心场基坑开挖设备进行粉质黏土基坑开挖的离心模型试验,再现粉质黏土地基中悬臂支挡基坑变形破坏的全过程,并记录开挖过程中基坑位移、支挡结构应变、土压力等,根据试验结果分析开挖条件下粉质黏土基坑变形规律和支挡结构土压力特性。
1 离心模型试验
1.1 试验设备
离心模型试验在清华大学土工离心机上进行,其有效半径为2 m,最大离心加速度为250g。使用文献[15]研制的离心场基坑开挖设备,可在离心场真实应力路径条件下实现基坑开挖。开挖设备固定在模型容器上,模型容器由铝合金制成,长60 cm,宽20 cm,高55 cm,见图1。模型容器的一侧装有一块厚的透明有机玻璃,用于在试验时观察模型变形。

图1 基坑开挖试验模型示意(单位:cm)
1.2 试验模型
试验在50g的离心加速度场中进行。挡墙的埋置深度为14 cm,基坑的开挖深度为22 cm,埋深比(埋置深度与开挖深度比值)为1∶1.6。
试验所用的粉质黏土的土粒相对密度为2.7,液限为25%,塑限为18.5%,土坡模型的击实干密度控制在1.55 g/cm3,含水率为18%。制样前先按照试验方案调整好固定挡墙位置,然后分层击实地基,完成后嵌入挡土墙,固定挡墙后将左侧地基开挖至设计深度。根据待开挖土体的质量确定设备竖向加载板的质量后,将开挖设备安装到模型箱上。将横向的支撑板调整到与挡墙刚好接触的位置,竖向加载板则置于左侧地基土上,最后解除对挡墙的临时固定,试样制备完成。
试验采用的挡墙为实心铝板,其高度为40.0 cm,宽度为19.6 cm,厚度为1.0 cm,弹性模量为70 GPa。挡墙宽度略小于模型箱宽度以保证开挖时挡墙可以自由移动,不受模型箱壁的影响。根据抗弯刚度等效原则,该模型挡墙在50g离心加速度下相当于厚度为650 mm的钢筋混凝土挡墙。
1.3 测量技术
试验采用离心场高质量图像采集与位移测量系统记录挡墙与土体的变形过程。通过图像相关分析可以得出挡墙位移分布、土体位移场、任意点的位移时程等。此外,试验中使用激光位移传感器测量挡墙顶部的水平位移。
挡墙两侧表面沿竖直方向设置若干圆柱形孔槽,用于布设土压力传感器。土压力传感器内嵌于孔槽内,受力面与挡墙表面平齐,尽可能消除局部土拱效应带来的误差。此外,挡墙两侧粘贴了14对应变片,记录试验过程中挡墙不同高度的应变。根据弹性理论,利用实测应变可以得到挡墙的弯矩。挡墙上传感器的具体布置参见图1(b)。
1.4 试验步骤
在进行基坑开挖离心模型试验时,离心加速度从1g开始逐渐增加至50g后,控制离心加速度保持稳定一段时间,待模型变形稳定后,通过远程控制系统向开挖设备发送开挖指令,支护板后撤离开挡墙,同时竖向加载板上提完成开挖。当基坑支护系统破坏或模型不再变形时,试验结束。试验过程中通过图像采集系统、位移传感器、土压力传感器及应变片测量和记录模型变形、挡墙顶部位移、挡墙上作用的侧土压力及挡墙应变。
2 支挡结构响应
基坑内土体开挖时,支挡结构因两侧土压力差而产生侧向变形。挡墙顶部水平位移的时程曲线见图2。可知:基坑开挖后挡墙水平位移随时间增长显著增加且增加速率逐渐减小并趋于稳定;图像测量和激光位移传感器测量的结果吻合较好,验证了图像测量方法的有效性。
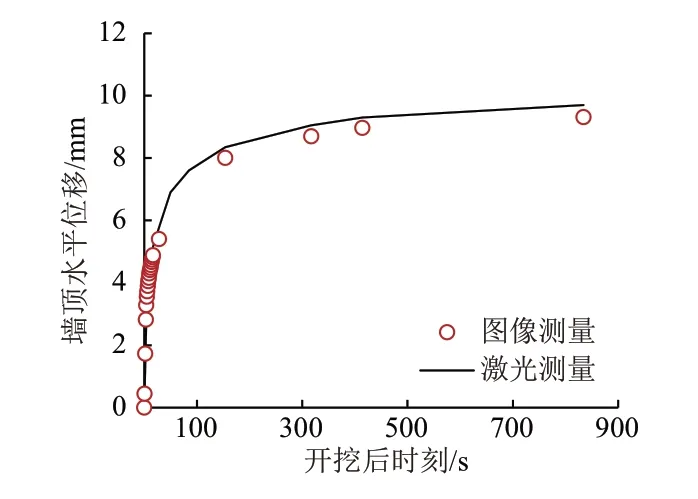
图2 挡墙顶部水平位移时程曲线
不同时刻挡墙水平位移沿深度分布曲线见图3(a)。可知:基坑开挖引起挡墙变形的模式主要为向坑内的偏转,并伴随一定的弯曲变形。随挡墙顶部水平位移增长,挡墙挠曲变形增大,转动中心深度增加,说明随挡墙位移增长,挡墙和填土之间的相互作用加强,相互作用范围加深。
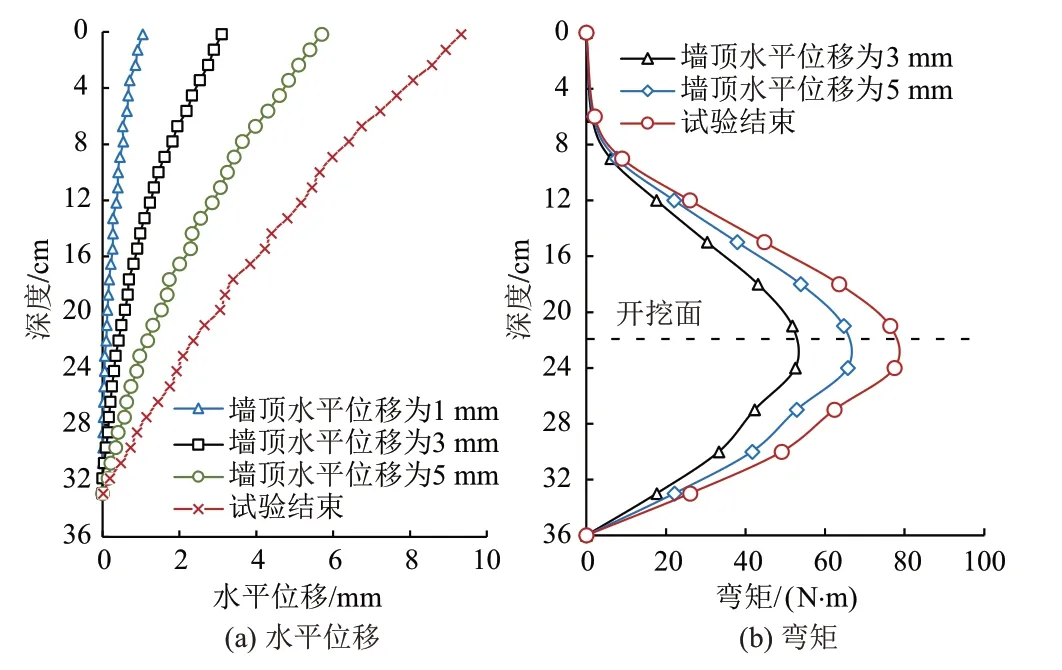
图3 不同时刻挡墙水平位移、弯矩沿深度分布曲线
开挖后不同时刻挡墙弯矩沿深度分布曲线见图3(b)。可知:弯矩分布呈现出近似抛物线分布,峰值出现的位置略低于开挖面。随着挡墙顶部水平位移增大,挡墙弯矩增大,但最大弯矩所在位置几乎不变,即挡墙最危险截面的位置几乎不随挡墙位移发生改变。
3 基坑变形特性
试验结束时模型见图4。可见,开挖完成后填土内部产生了两条竖直裂缝,分别距挡墙12、23 cm,而在挡墙和填土之间没有产生裂缝,此现象与朗肯土压力理论中挡墙和填土之间会产生裂缝的认定不同。两条裂缝最终的深度相近,大约为6 cm。朗肯土压力理论中裂缝深度z0的计算公式为z0=2ctg(45°+φ/2)/γ,其中c为土黏聚力,φ为土内摩擦角,γ为土重度。据此计算的裂缝深度为5.8 cm,与试验测得的裂缝深度接近。

图4 试验结束时模型
基于位移测量精度,本文将水平位移0.1 mm的等值线作为基坑变形区边界。基坑变形过程中墙后支护土体水平位移等值线见图5,其中ut为挡墙顶部水平位移。可知,随着挡墙偏转,墙后填土的位移增加,变形区向深部扩展。进一步分析表明,基坑变形具有明显的阶段性特征。当挡墙水平位移较小时(ut=1 mm),基坑变形较小,变形集中在填土上部靠近挡墙区域,位移分布较均匀;随着挡墙进一步偏转(ut=3 mm),土体变形区向深部扩展,土体上部水平位移等值线变密并出现了张拉裂缝;随着挡墙继续偏转(ut=5 mm),张拉裂缝不断扩展,宽度和深度增加,此阶段基坑变形以张拉变形为主;挡墙顶部水平位移从5 mm增大至9 mm的过程中,水平位移等值线进一步密集,裂缝宽度继续扩展,但深度不再变化,变形区逐渐稳定,裂缝与挡墙间的部分土体发生滑动变形,此阶段基坑变形以滑动变形为主。综上,开挖引起的墙后土体位移依赖于挡墙的位移模式和大小。

图5 不同墙顶水平位移时支护土体水平位移等值线
不同深度土体水平位移和竖向位移沿水平方向分布见图6。可知:填土水平位移和竖向位移变化趋势相同,均随深度增加而减小。在同一深度上,靠近挡墙区域的土体水平位移较大,而远离挡墙区域的土体水平位移较小。位移水平分布曲线上存在一个位移由小变大的转折点,如果曲线的转折点不明显,则在变化趋势不同的两段曲线取切线,采用其交点作为转折点。这说明挡墙和转折点之间的土体发生了较为明显的滑动变形。不同深度处转折点的位置在图6中用红色虚线标出,将不同高度处的拐点相连,可以组成基坑变形的滑动区。

图6 不同深度土体水平和竖向位移沿水平方向分布
不同挡墙顶部水平位移时填土滑动区的边界见图7。可知,随着挡墙偏转,滑动区边界和变形区边界一样不断向下扩展,当挡墙顶部水平位移到达一定值(ut=5 mm)后,填土滑动区边界逐渐稳定,形成较为明显的滑楔体。当挡墙顶部水平位移继续增加时,滑楔体边界不再改变,但滑楔体内部土体的变形继续增加,与周围土体产生更大的相对位移。滑动区在变形区内部,和变形区相比较,滑动区边界线较陡,下边界点略高于变形区。

图7 不同时刻土体滑动区和变形区边界
4 支挡结构土压力特性
不同深度处挡墙的土压力随挡墙顶部水平位移的变化见图8。可知:随挡墙顶部水平位移增长,各点土压力减小,且下降速率逐渐减小,直至趋近于0,位移继续增长土压力保持不变。

图8 挡墙上土压力变化值随挡墙位移变化
挡墙上土压力沿深度分布曲线见图9。可知,上部由于张拉裂缝的产生,土压力的值非常小;土压力沿深度近似呈抛物线分布,极值点在4H/5(H为挡墙高度)处,这会导致合力的作用点高于朗肯土压力三角形分布时的作用点。
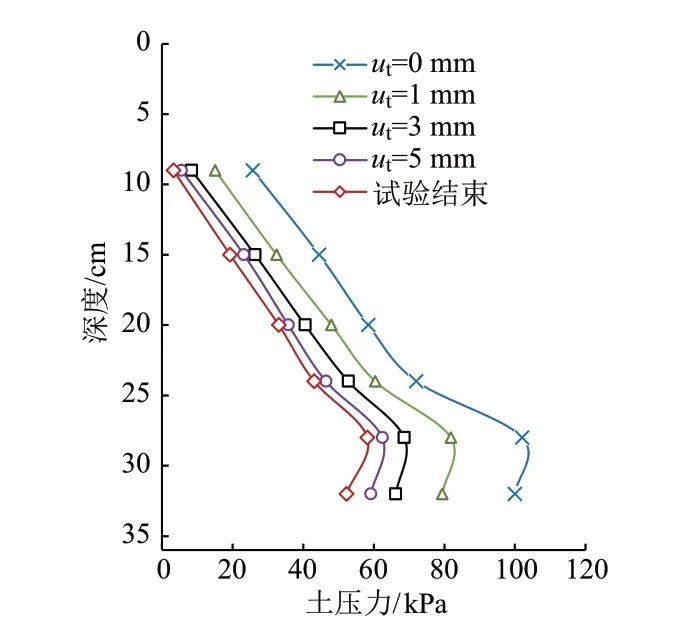
图9 不同时刻挡墙上土压力沿深度分布曲线
5 结论
1)基坑开挖后,挡墙会朝坑内发生偏转,并伴随一定的挠曲变形。
2)开挖导致的基坑位移依赖于挡墙的位移模式和大小,其过程具有明显的阶段性,可分为小变形阶段、张拉变形阶段和滑动变形阶段。
3)墙后填土的滑动区位于变形区内部,和变形区一样随挡墙偏转不断向深部扩展。当挡墙位移到达一定值后,变形区和滑动区边界逐渐稳定,不再随挡墙位移增长而改变。
4)挡墙和填土界面上没有产生裂缝,张拉裂缝仅在填土内部产生,裂缝深度可用朗肯土压力理论公式计算。
5)开挖过程中,挡墙上土压力随挡墙位移增加而下降,且下降速率逐渐减小,直至土压力达到极小值。土压力沿深度方向近似呈抛物线分布,极值点大致在4/5倍挡墙高度处。
