基于ARIMA和SVM混合模型的流感新增病例预测
2022-02-12李荣庭范莲静
李荣庭,段 鹏,胡 瑞,范莲静
(云南民族大学 数学与计算机科学学院,云南 昆明 650000)
根据以往的经验,我国冬季流感流行时间一般从12月份开始一直持续到来年的3—5月.经中国疾病预防控制中心病毒预防控制所首席专家武桂珍的介绍由于流感和新冠肺炎均可经呼吸道飞沫传播及接触传播[1-4],其均受气候以及人际接触等的影响较大:秋冬季节的低温天气会使呼吸道排入外界的病毒存活期延长,且在寒冷刺激下,人的抵抗力相对较弱,病毒趁虚而入,易于形成传播;人员聚集,则是疫情扩大的另一必要条件[5].进入秋冬季之后,全国更大范围的复工和学生开学,会形成广泛的、不同程度的人员聚集,且秋冬季节里人们室内活动相对频繁,室内通风情况不及夏季.加之目前全球范围内许多其他国家的新冠肺炎疫情仍较严峻,尚未得到有效控制等,以上这些因素均可能导致我国在今年冬季面临新冠肺炎疫情的反弹,其反弹时间也将很可能与冬季流感流行时间重叠[6].倘若我们能在流感发现早期及时预测疾病的增长趋势,很有可能我们就可以采取相应的措施,及时止损.同时权威精准的预测也可以使人们尽早的把预防流感重视起来,从而进一步减少流感蔓延的规模,从而也从侧面对新冠疫情的防控起到了积极作用.本课题虽然是以甲型H1N1流感为案例进行预测分析,但搭建构造的模型,其实亦适用与其他类似的传染病,例如肺结核、新冠肺炎等.对于后续的相关研究,起到了一定的借鉴作用.从另一个角度出发,也可以用此模型对未来可能出现的潜在的传染病威胁进行排查.
目前现代医学技术取得重大发展,但诸多传染性疾病仍是人类社会向前发展的重要阻力之一.查阅全世界范围内已有的流感相关数据进行分析研究,多数预测模型应用多元线性回归、LASSO回归以及Ridge回归模型结合相关检索词数据进行建模分析,探讨回归模型与流感疫情预测的相关性与可行性[7].常见的传染病预测模型还有灰色模型、Markov模型、人工神经网络模型、通径分析模型等[8].但这都需要大量数据作为支持才能得到理想的结果,而针对突如其来的大规模传染病,其预测数据量小、预测结果亟待使用的特点对预测工作的准确度和速度提出了双重要求.基于上述要求,实验选取少样本数据集,利用数据变化的自回归过程建立模型,使得搭建的模型具有较高的可信度及一定的实用性.
1 模型介绍
1.1 ARIMA模型
时间序列是利用统计学的基本原理,通过对数据的采集选用模型以近似估计,利用模型分析揭示数据的内在特性[9],达到推测发展趋势规律的目的[10].自回归差分移动平均模型(ARIMA)是常用的时间序列之一.该模型主要分为三个过程,平稳过程(I)、自回归过程(AR)和移动平均过程(MA).该模型反映了时间序列过去与现在,未来与现在之间的关系,适用于短期预测,需要的数据量小、参数少,这与少样本数据集训练有很高的锲合度.基于上述特点,ARIMA模型在众多领域的应用都有着不错的变现,尤其是在与时间相关的预测方面[11].
1.2 SVM模型
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器.SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题.SVM的的学习算法就是求解凸二次规划的最优化算法[12].相比于传统的优化算法,例如人工蜂群算法、蚁群算法、粒子群算法,SVM的优化对象不仅可以是固定参数也可以是其他数值.ARIMA模型里的关键参数都是通过模型自身的差分值进行自调整的,无需再优化,对于下文中动态残差的优化,SVM算法较为合适.
2 基于ARIMA-SVM模型的预测算法
2.1 ARIMA模型搭建
本文通过将2009年美国甲型流感新增病例数据与传统ARIMA模型结合[13],并在此基础上增加模型评估环节以确定阶数,绘制修改后的流程图如下.

图1 ARIMA模型构建流程示意图
传统ARIMA模型在阶数选择方面,一般采用置信度区间能够完全覆盖的数值,但是往往没有容忍度的参数选择会使模型错过最佳参数,故本文加入模型评估,为确定阶数增加一些弹性,使得模型在可接受范围内忽略一些误差从而找到最佳参数.
2.1.1 平稳数据
流感的传播具有聚集性和爆发性,所以针对数据的区域特点和时间特点,考虑到模型对数据平稳性的要求[14],将美国2009年甲型H1N1新增病例数数据利用差分法进行平稳,计算特征点数据方差,找到合适的差分阶数,下图2为差分比较图.
通过图2内容可以看出,一阶差分后数据相对稳定.又根据差分后的过滤掉空值缺失数据绘制效果展示图.由图3可知差分后的平稳性要比原数据好很多,标准差反映出差分后的数据的离散程度在可接受的范围[15],故确定ARIMA模型的参数d=1.
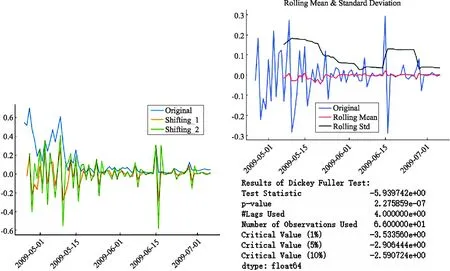
图2 一、二阶差分效果展示图 图3 差分数据效果展示图
2.1.2 自相关图和偏自相关图的分析
本文利用自相关函数(ACF)和偏自相关函数(PACF)结合赤池准则(AIC)和贝叶斯信息准则(BIC)进行模型评估确定相应的阶数p和q,下图4中的阴影表示置信区间,可以看出不同阶数自相关性的变化情况,从而选出p值和q值.p值代表预测模型中采用的时序数据本身的滞后数(lags),也叫做AR(auto-regressive)项.q值代表预测模型中采用的预测误差的滞后数(lags),也叫做MA(moving average)项[9].
针对p值和q值得选取,本模型提出利用Matlab软件对自相关函数图像和偏自相关函数图像进行拉普拉斯(Laplace)滤波处理抽离置信区间和阶数取值特征点,然后用cftool工具箱中的傅里叶函数和高斯函数分别进行拟合得到置信区间边界函数s(x)和阶数取值函数F(x).(由于置信度区间关于x轴大致对称,所以本文选取x轴上方的部分,抽象出置信度区间边界函数s(x)).

图4 自相关函数和偏自相关函数选取p、q值
(1)
p值和q值的确定原则是,图像中置信区间所涵盖的最后一个超出其范围的滞后数的取值.但在原有的模型中p值和q值的选取是没有容忍度的,即只有完全符合置信区间要求才会被选取.本文在此基础上提出利用容忍度函数,如公式(1),筛选符合条件的最小的p值和q值以保证不会使模型陷入局部最优而导致忽略全局最优.其中xi是待定p或q.根据上述图像和公式本确定的p值为3,q值为2.
2.1.3 AR模型与MA模型
根据之前确定的差分阶数还有p值和q值,建立如下数学模型:
(2)
(3)
(4)
其中,yt是当前值,μ是常数项,p是阶数,γi是自相关系数,εt是误差,θi能够消除波动的最佳参数.从实际情况出发由于自回归模型本身的限制,在数据选取过程中既要保证稳定性,还要保证自相关性,如果自相关系数φi小于0.5,则不宜采用[13].
2.1.4 模型残差检验
基于以上模型,进行模型残差检验,观测ARIMA模型方差是否为常数的正态分布,以确保模型的可行性和合理性[16].并通过对其准确的预测采取下一步相应的预防措施.在选择了合适的参数之后,对ARIMA模型的残差进行初步预测,如图5.
2.2 SVM模型残差优化
2.2.1 SVM优化分析
根据上文中给出的相关图像,不难看出预测数据与实际数据还存在这一定的误差.故针对预测中存在的误差本实验欲通过支持向量机(Support Vector Machine,SVM)进行优化[17].根据上文,本实验选取原模型残差作为对象进行优化,并综合两个模型的实验结果得出混合预测值作为最终预测值[11],图6为优化过程流程图.对于图6混合预测值的详细解释参照下文残差数据导入部分.
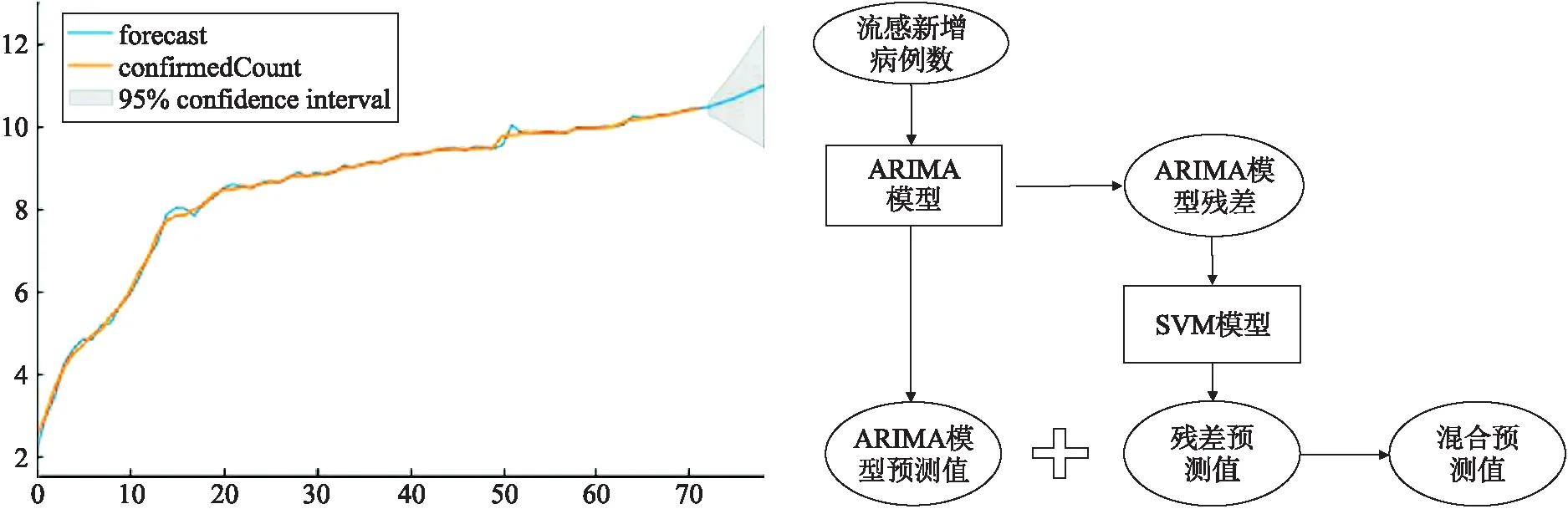
图5 残差预测效果图展示 图6 加入SVM模型优化后的ARIMA模型流程示意图
具体优化的操作步骤主要分为3个部分,第1个部分根据之前ARIMA模型预测数据与实际数据做差得到新的误差数据并利用numpy第3方库进行矩阵化为误差数据贴上时序标签,如公式(5);第2部分将得到的新的数据再做滑动处理扩增数据集,滑动次数按照参照之前ARIMA模型得出的,这样就得到了新的矩阵,共计63行5列如图7所示;第3部分将实际数据的误差作为标签利用SVM模型进行有监督的学习,具体操作流程参下.
Eerror=yreal-yarima
(5)
2.2.2 导入SVR模块
由于当前环节需要处理的数据是预测值与实际值的误差,那么自变量就可以定做是出现新增病例之后的每一天,与此同时因变量也自然而然成了误差本身.在此基础上就不难推断在进行优化之前需要导入SVR模块[15],SVR()就是SVM算法来做回归用的方法(即输入标签是连续值的时候要用的方法),通过以下语句来确定SVR的模式(选取比较重要的几个参数进行测试).
1) kernel:核函数的类型
一般常用的有rbf函数,linear函数,poly函数,如图7所示,将数据导入函数拟合图像发现rbf函数图像与实际数据拟合度最高,故最佳核函数为rbf函数[18].
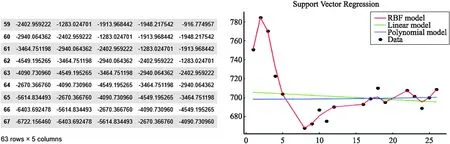
图7 误差数据最终形式 图8 核函数与数据贴合度参考图
2)C:惩罚因子
C表征对离群点的重视程度,C大小与重视程度成正比,与对误差分类的惩罚成正比,与margin成反比.当C趋近无穷的时候,表示不允许分类误差的存在,容易过拟合;当C趋于0时,表示我们不再关注分类是否正确,容易欠拟合.
3)gamma
gamma是rbf函数的核系数且gamma的值必须大于0,其作用是保证模型不会过拟合.
综上所述SVR模块的几个重要参数可以由上述规则基本确定:
SVR(C=10, cache_size=200, coef0=0.0, degree=2, epsilon=0.1, gamma=‘scale’, kernel=‘rbf’, max_iter=-1, shrinking=True, tol=0.001, verbose=False)
2.2.3 残差值数据导入
首先要将每日的预测值,转化为矩阵形式,方便将数据导入SVM.由于目前本实验无法确定优化后的效果优秀与否,故要同时考虑原始ARIMA模型的预测值yarima与ARIMA-SVM模型的预测值yarima-svm,如公式4.然后将总预测值减去实际值,得到残差值E,即公式5.在此基础上将残差值导入SVR模块,为了筛选出最合适本数据集的C和gamma,还要引入一个新的变量[12],记作最小残差Emin.一方面初始Emin是为了拿来和E进行比较,缩小检索C和gamma的范围,保证筛选范围不会太大,导致程序崩溃.另一方面,并将循环中出现的最小E赋值给Emin,循环最后找到Emin对应的C和gamma,记作Cbest和gammabest流程图如图8.
ysum=yarima+yarima-svm,
(6)
(7)

图9 SVM参数调整流程图
3 实验与分析
实验数据采用WHO官网公开的美国2009年甲型H1N1流感数据集,实验选择配置为AMD Ryzen 5中央处理器(主频 3.4 GHz),内存为8G的电脑为硬件平台,在 Windows 10,64位操作系统下利用anaconda(python3.7.2)进行实验.将上述过程中得到的最佳最佳参数分别导入到ARIMA和SVM模型中,便可以得到较为准确的预测结果了.
3.1 数据集
本文使用的数据来自世界卫生组织WHO(World Health Organization)公开下载数据集.对数据进行了如下处理:①考虑到地方防疫措施和疫苗推广对疫情的影响,本实验选取2009年疫情初期4月24日到7月16日共计 83 d,美国甲型H1N1新增病例数信息(其中有 4 d 空值);②数据清洗,取空值前后2天的平均值填充;③将数据集按4∶1比例分割为训练集与验证集.
3.2 基于ARIMA和SVM模型的预测
3.2.1 ARIMA模型预测结果
将2009年4月24日以来到7月6日之间美国甲型H1N1流感新增病例数数据导入到已经初步搭建好的时间序列模型,并利用python软件绘制出模型差分值图像,如图9所示.并将差分后的数据导入传统ARIMA模型预测结果如图10.

图10 ARIMA模型数据的差分值 图11 ARIMA模型预测效果示意图
很明显预测结果存在较大偏差,其中原因有可能为以下2点:
1) 在偏离处当地相关部门采取了有效的防控措施,使得实际新增病例数远远低于预测值.
2) 模型本身仍存在一定缺陷,需要进行进一步的优化.
基于上述原因,本文提出了利用SVM模型对残差值进行改进的方案.
3.2.2 ARIMA-SVM模型优化结果
根据上文中SVM对残差值的优化,将新的预测模型预测值、旧的预测模型预测值、真实的新增病例利用python中的画图工具绘制甲流新增病例变化趋势折线图12用于进行相互比对.
3.2.3 模型结果评估
为了考察新模型预测效果,本实验引入平均绝对百分误差(MAPE)和均方根误差(RMSE)2个指标来测定模型预测的精度.其中MAPE表示预测结果每天的预测结果与当天实际情况的偏离指数,RMSE表示总体预测结果与实际情况的偏离指数.故MAPE和 RMSE越小,预测精度越高.公式与对比见表1:
(8)
(9)

图12 各模型预测结果对比图

表1 新旧模型残差评估表
通过上面的表格和对比图,不难发现改进后的模型精准度大大增加了,疫情病发的 50 d 内,预测数据与实际数据基本重合,准确率非常高,50 d 之后预测与实际情况开始出现偏差,但走势相对吻合.
查阅相关资料2009年6月11日(即疫情出现 50 d 以后),WHO将甲型H1N1警戒级别从5级提高到最高级6级.这是WHO 40年来第1次把传染病警戒级别升至最高级别.世卫生组织确认全球75个国家和地区,共确诊27737例患者,死亡141例.至此美国人民危机意识已经防疫意识有了本质上的觉醒,自觉在家隔离,相关部门加强卫生管理.猜测这可能是导致疫情增长状况出现拐点与预测数据产生偏差的本质原因.正如王菊[19]博士所说,独立、透明、有效和及时的信息流对于国际社会控制不断出现的疾病至关重要.随着甲型HIN1流感的细节开始被披露,人们应对农业尤其对墨西哥的猪养殖业进行一个更加全面的评估,这对于为未来吸取经验教训至关重要.当然,人们目前的注意力集中在国际社会公共卫生反应,为疫情作准备意味着为意外作准备,在不确定的情况下作出快速和有效的反应.正如应对禽流感的经验教训所表明的那样,这可能需要采取更多的措施,而不只是从上至下的“积极和有力”的技术应对措施.本文的实证分析为上述卫生结论提供有力证明.
4 结语
本研究基于2009年在美国和墨西哥等地大面积爆发的甲型H1N1流感新增病例数据,展开关于传染性肺炎的研究,通过ARIMA -SVM模型预测得知甲型H1N1流感新增病例人数明显高于实际值,这可能与当年当地各国医疗工作者展开的防治工作有关,本研究结果也为甲型H1N1流感防治措施的有效性提供了间接证据,为之后的传染病预防工作提供参考,从而达到及时判断、抉择和控制的目的.
根据4月24日到7月16日数据本实验针对传统ARIMA模型进行改进:①提出利用图像拟合函数得到了最佳p值和q值;②利用ARIMA预测值与实际值之间的残差序列作为样本集,导入支持向量机(SVM)预测残差,建立ARIMA-SVM混合模型;③在SVM优化过程中加入参数自循环得到最佳惩罚因子和支持向量数;④通过比较新的评估参数MAPE和RMSE,发现支持向量机有效拟合了原始序列的非线性部分,ARIMA-SVM混合模型的预测效果优于单一ARIMA模型.
针对本模型可以做的进一步研究工作:①优化ARIMA模型的数据平稳过程;②本模型应对噪声的自适应性较差,如果在预测的过程中数据被其它人为因素影响会导致预测误差变大,故在去噪方面可以进一步改进;③ARIMA模型研究的对象只与时间有关,但在现实社会中,流行性传染病的传播受医疗水平、文化、经济等多种因素的影响,在本模型的基础上可以加入人口演化,医疗隔离等仿真模型,使得模型精度进一步提高.
