改进的PrefixSpan算法在旅游热门路线上的应用
2022-02-12胡冰冰芦俊丽郑承宇
胡冰冰,芦俊丽,郑承宇
(云南民族大学 数学与计算机科学学院,云南 昆明 650500)
旅游业在地区经济增长中一直发挥着重要作用,它能带动地区经济发展和资金的积累,促进信息技术的传播,增加就业机会等[1].随着经济的发展和生活水平的提高,喜爱旅游的人变得越来越多,而旅游路线的选择是人们出发前研究的一个重要问题,是旅游中至关重要的一个环节[2-3].为了使游客游览的内容丰富多彩、避免迂回和往复等问题,旅游路线的规划对于游客至关重要.
随着互联网的发展和时代的进步,越来越多的游客喜爱通过游记的形式在旅游平台上分享自己的旅游经历,游记中含有大量不同游客的独特体验和可靠的出行建议,为挖掘旅游热门路线提供了极佳的参考依据.然而,由于用户量的日益增加,各大旅游网站游记数目也日益庞大.从爆炸式增长、庞杂多样的游记中,获取历史游客的游览信息进行旅游路线推荐,成为了目前旅游路线推荐的研究难点[4].
笔者提出一种改进的PrefixSpan算法来挖掘旅游热门路线.首先从携程旅游网站(https://www.ctrip.com/)爬取大量游记记录,对游记数据进行预处理,获取旅行轨迹数据库.然后,采用改进的PrefixSpan算法对数据进行挖掘,得到旅游热门路线.与原算法相比较,改进的PrefixSpan算法连续性更好,比原算法效率更高,更适用于旅游路线的搜索.
1 相关工作
旅游路线问题一直被国内外学者所重视.目前,许多学者对旅游热门路线进行了深入研究,并取得了一批有价值的研究成果.2020年董飞[5]基于0-1规划模型为旅游团设计旅游路线,该路线主要考虑的是在时间的限制下,给出旅游团游览景点的最大时长路线.同年郭斌等[6]提出一种基于群智数据的跨模态分析与情境关联旅游路线推荐方法.首先使用跨模态分析方法将互补的图像与文本相结合,再进行分类识别,然后基于图模型使用PhotoRank算法优选出具有多样性、代表性的图片,最后采用关联规则挖掘,得到针对不同出行人群的特定需求情境的推荐路线.同年袁绛书等[7]针对黄山景点众多且过于分散,游客没有办法在有限的时间内游览完期望景点的问题,建立了基于游客满意度最大化的旅游路线优化模型,此模型考虑了距离、年龄、性别、金钱和用户偏好等元素,利用贪心算法求解,最终给出游客满意度最大的最优路线.
旅游热门路线的好坏与旅游轨迹数据的来源和获取方式息息相关.目前,旅游轨迹的搜索方式主要有以下几种:2015年Sobolevsky等[8]通过银行卡终端获得的交易数据来建模旅行者的空间和时间移动模式.这些方式所收集数据要么在数量和地理区域上有限,要么不能免费提供给公众使用.2017年Vu等[9]以及2020年Kolahkaj等[10]使用Flickr软件,通过处理带地理标记的照片来得到旅游轨迹,此软件虽然免费但毕竟不是旅游软件,不能保证提取的数据全是游客的旅游轨迹,且上传的旅游图片只包含旅游路线的部分地点,不是完整路线.互联网旅游平台的游记是对旅游过程的完整描述,作为当今最热门的软件,得到越来越多旅游研究者的重视[4, 6, 11].
序列模式挖掘是指从序列数据库中挖掘出现频率高的模式,序列模式挖掘问题首先由Agrawal和Srikant在1995年提出,并给出了基于类Apriori的AprioriSome,AprioriAll和DynamicSome 3种序列模式挖掘算法[12],随后他们又提出了AprioriAll算法的扩展算法:广义序列模式(Generalized Sequential Pattern,GSP)挖掘算法[13],该算法的特色是引入了时间约束、滑动时间窗和分类层次技术,增加了扫描的约束条件.而此类基于类Apriori的算法的缺点是产生大量的候选项集合和必须重复扫描数据库.序列模式挖掘的模式增长方法FreeSpan算法[14],以及它的前驱算法PrefixSpan算法由Han等[15]提出,其中PrefixSpan算法因包含更少的投影库和子序列连接,数据库收敛更快,算法效率比之前的算法效率都高,而被广泛应用于序列模式挖掘中[16-19].
基于模式增长策略的PrefixSpan算法是现有的序列模式挖掘算法中性能最好的算法之一,它不需要产生候选的序列模式,大大缩减了算法运行需要的存储空间.为提高PrefixSpan算法的效率以及适应于各种应用,很多学者提出了一些改进算法.2019年Ganaphy等[17]对PrefixSpan算法进行改进,应用于挖掘交通序列模式和基于交通序列规则的交通量预测.2019年Niyazmand等[18]对PrefixSpan算法进行改进,应用于发现不同洪水情况下的报警模式.2021年,Wang等[19]针对传统的序列模式挖掘算法Prefix span存在时效性差、阈值均匀等缺点,提出了TVI-Prefixspan算法来挖掘传销模式,实验结果表明,TVI-Prefix span算法在效率和挖掘效果上均优于传统的序列模式挖掘算法.
序列模式挖掘在旅游热门路线上有着广泛的应用,研究者们对其开展了很多学术研究和探索.比如2017年,Vu等[9]使用Top-k序列规则挖掘算法[20]来挖掘旅游目的地,然而此算法不能有效的挖掘完整的旅游热门线路.2019年孙文平等[21]利用PrefixSpan算法来挖掘旅游热门景点,虽然挖掘到的景点有着时间先后关系,但是不具有线路的连续性.
2 PrefixSpan算法
2.1 基本定义
PrefixSpan算法的基本思想是使用递归的策略,从1阶前缀开始,不断用频繁的前缀划分搜索空间,得到相应的后缀数据库,在后缀数据库上进行支持度统计并得到1阶频繁序列.再扩展前缀,用高一阶的前缀划分空间,继续向前推进.就这样,前缀越来越长,后缀数据库中的后缀序列越来越短.最终,后缀数据库为空时,频繁序列搜索完毕.基于PrefixSpan算法的相关定义如下.
定义1(序列)s=〈l1,l2,…,lm〉是一个长度为m的序列,li(1≤i≤m)为序列的项,代表一个旅游地点,长度为m的序列为包含m个地点的旅游轨迹,称为m阶序列.
定义2(序列数据库)序列数据库S是元组〈sid,s〉的集合,其中,sid是用户ID,s是一个序列,即一个用户的旅游轨迹.
例1表1是一个旅游的序列数据库,s3=〈l1,l2,l6,l5〉是一个4阶序列,即用户依次旅游地点l1、l2、l6、l5的旅游轨迹.

表1 序列数据库
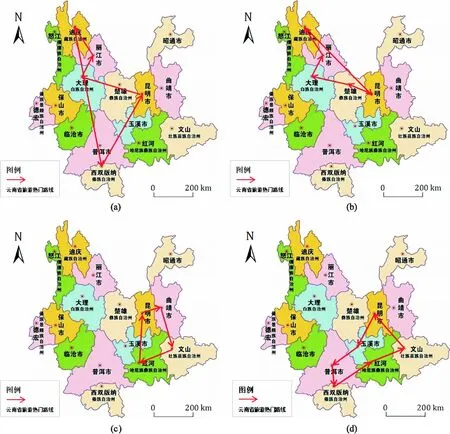
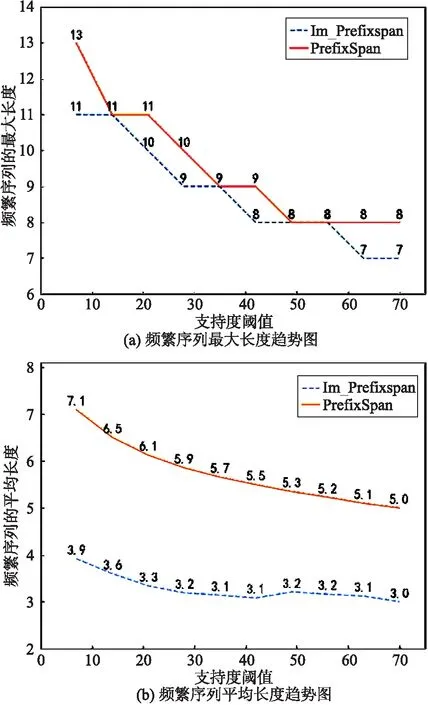
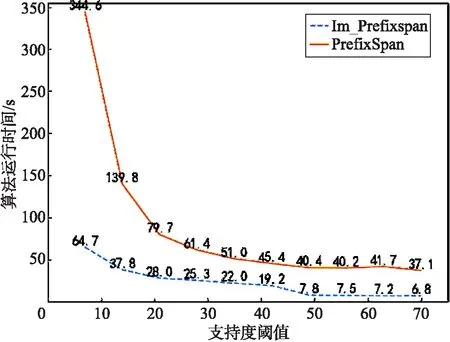
定义3(前缀及后缀)设序列A=〈a1,a2,…,am〉,B=〈b1,b2,…,bn〉(m 例2表2为s4=〈l2,l6,l7,l8,l3,l1〉的一些前缀和对应的后缀. 表2 前缀和后缀实例 定义4(后缀数据库及后缀数据库的支持度)设v为序列数据库S中的一个序列,则v的后缀数据库为v在序列数据库S中后缀的集合,表示为S|v,序列v在其后缀数据库中的支持度为序列数据库中包含S|v的序列个数. 例3序列〈l6,l7〉在表1序列数据库S中的后缀数据库如表3所示,即S|〈l6,l7〉={〈l5〉,〈l8,l3,l1〉,〈l4,l2,l1,l5〉},序列〈l6,l7〉在其后缀数据库中的支持度为3. 表3 后缀数据库实例 定义5(频繁序列)如果序列v在后缀数据库S中的支持度不低于给定阈值min_support,则称序列v为频繁序列. 2.2.1 PrefixSpan算法实例 下面以表1给出的序列数据库S及min_support=2为例来描述PrefixSpan算法挖掘频繁序列的过程. Step 1 扫描序列数据库S一次,找到所有的1阶序列,对其进行计数.它们分别是〈l1〉:5、〈l2〉:5、〈l3〉:4、〈l4〉:2、〈l5〉:4、〈l6〉:5、〈l7〉:3和〈l8〉:1,其中符号“〈序列〉:计数”表示序列和它的支持度计数.〈l8〉的支持度低于2,将〈l8〉从序列数据库中删去,即s4=〈l2,l6,l7,l3,l1〉. Step 2 用每个频繁的1阶序列作为前缀来划分空间,构造相应的后缀数据库,如表4所示. Step 3 对于每个1阶前缀,统计后缀数据库中各项的支持度计数.出现在后缀数据库中1阶前缀后面的项都要统计其支持度,不管是否相邻.例如:在后缀数据库中〈l3〉前缀后面出现的项有〈l1〉、〈l2〉、〈l3〉、〈l4〉、〈l5〉、〈l6〉和〈l7〉.将满足支持度计数的项〈l1〉、〈l2〉、〈l5〉和〈l6〉与当前前缀〈l3〉进行合并,得到新的前缀〈l3,l1〉、〈l3,l2〉、〈l3,l5〉和〈l3,l6〉. Step 4 以新的前缀〈l3,l2〉为例来说明后续挖掘过程,扫描以〈l3〉为前缀的后缀数据库,构造以〈l3,l2〉为前缀的后缀数据库,统计新的后缀数据库中各项的支持度计数.统计支持度时和Step 3相似,出现在〈l3,l2〉后面的项都要统计,不管是否与〈l3,l2〉相邻.结果如表5第1行所示. Step 5 将满足支持度计数的项〈l1〉、〈l5〉分别与〈l3,l2〉进行合并,得到新的前缀〈l3,l2,l1〉和〈l3,l2,l5〉,如表5第2、3行所示. 表4 PrefixSpan算法的一阶频繁序列及后缀数据库 表5 以〈l3,l2〉为首的频繁序列及后缀数据库 Step 6 此时以〈l3,l2,l5〉为前缀的后缀数据库中没有满足支持度计数的单项,即停止对〈l3,l2,l5〉的扩展.在以〈l3,l2,l1〉为前缀的后缀数据库中,将满足支持度计数的项〈l5〉与前缀〈l3,l2,l1〉进行合并,得到新的前缀〈l3,l2,l1,l5〉,此时以〈l3,l2,l1,l5〉为前缀的后缀数据库中没有满足支持度计数的单项,即停止对〈l3,l2,l1,l5〉的扩展.即以前缀〈l3,l2〉为首的频繁序列为〈l3,l2〉、〈l3,l2,l1〉、〈l3,l2,l5〉、〈l3,l2,l1,l5〉. Step 7 以〈l3〉为首的其他前缀的扩展过程同理,以〈l3〉为首的频繁序列为:〈l3〉、〈l3,l1〉、〈l3,l2〉、〈l3,l5〉、〈l3,l6〉、〈l3,l1,l5〉、〈l3,l2,l1〉、〈l3,l2,l5〉、〈l3,l5,l6〉、〈l3,l6,l5〉、〈l3,l6,l7〉、〈l3,l2,l1,l5〉和〈l3,l6,l7,l5〉. 2.2.2 连续性问题分析及改进策略 将PrefixSpan算法应用于旅游序列数据库中,会出现连续性问题.比如例5中得到的频繁序列〈l3,l2,l5〉,虽然〈l3〉、〈l2〉与〈l5〉在序列数据库中有着先后顺序关系,可是运用在旅游路线上,〈l3〉、〈l2〉与〈l5〉之间并不直达,频繁序列〈l3,l2,l5〉作为一个旅游热门路线就没有意义,本文对这种不连续关系做了优化改进. PrefixSpan算法应用在旅游热门路线挖掘中,需要充分考虑路线的连续性,主要有两方面不足需要改进: 第1,PrefixSpan算法对于1阶不频繁序列,将其直接从序列数据库中删除,这会导致数据库中包含此序列的序列不连续,进而导致挖掘出的结果存在误差. 第2,此算法在挖掘频繁序列时,对后缀数据库出现在前缀后的每个单项都进行支持度计数,不管它是否紧邻当前的前缀,忽略了序列的连续性.挖掘出的频繁序列跳过了一些地点,连贯性不足. 针对以上2个问题,本文将PrefixSpan算法进行如下改进: 第1,为防止出现不连续的现象,从序列数据库中删去1阶不频繁序列之后,再将其左、右子序列分别放回序列数据库. 第2,为了保证挖掘到的序列是连续的,挖掘频繁序列时,只对后缀数据库中各序列的首项进行支持度计数. 改进的PrefixSpan算法(本文称之Im_Prefixspan算法)的主要步骤如下: Step 1 扫描序列数据库S一次,找到所有的1阶序列,对其进行计数.如果某个1阶序列的支持度小于阈值,就将其所在序列以它为界一分为二,其左、右子序列分别放回序列数据库,并将原序列从序列数据库中删除. Step 2 用所有频繁的1阶序列作为前缀来划分空间,构造相应的后缀数据库. Step 3 对于每个L(L≥1)阶前缀,只扫描后缀数据库中序列的首项进行计数.如果支持度计数低于阈值,则将该首项对应的序列从后缀数据库中删去,停止对该首项的扩展. Step 4 将满足支持度计数的各个首项和当前的前缀进行合并,得到若干新的前缀. Step 5 令L=L+1,扫描当前后缀数据库,以新的前缀来构造相应的后缀数据库.返回到第3步,直至后缀数据库为空. 下面以表1中的序列数据库S及min_support=2为例,来描述Im_PrefixSpan算法挖掘过程. Step 1 扫描序列数据库S一次,找到所有的1阶序列,对其进行计数.它们分别是〈l1〉:5、〈l2〉:5、〈l3〉:4、〈l4〉:2、〈l5〉:4、〈l6〉:5、〈l7〉:3和〈l8〉:1.〈l8〉的支持度计数小于2,将其所在序列s4=〈l6,l7,l8,l3,l1〉,以〈l8〉为界分为s4.1=〈l6,l7〉和s4.2=〈l3,l1〉 2个左、右子序列,放回序列数据库,并将原序列s4从序列数据库中删除. Step 2 用〈l1〉、〈l2〉、〈l3〉、〈l4〉、〈l5〉、〈l6〉和〈l7〉分别作为前缀来划分空间,构造相应的后缀数据库,如表6所示. 表6 Im_PrefixSpan算法的一阶频繁序列及后缀数据库 Step 3对于每个1阶前缀,只扫描后缀数据库中序列的首项进行计数.以〈l3〉为例来说明,以〈l3〉为前缀的后缀数据库中,首项〈l1〉和〈l2〉的支持度计数低于阈值,则将对应的序列〈l1〉、〈l2,l1,l5,l6〉从后缀数据库中删去,停止对首项〈l1〉和〈l2〉的扩展. Step 4 将满足支持度计数的首项〈l6〉和当前的前缀〈l3〉进行合并,得到新的前缀〈l3,l6〉. Step 5 扫描以〈l3〉为前缀的后缀数据库,以新的前缀〈l3,l6〉来构造相应的后缀数据库,如表7所示.以〈l3,l6〉为前缀的后缀数据库中,首项〈l7〉满足支持度计数,将其和当前的前缀〈l3,l6〉进行合并,得到新的前缀〈l3,l6,l7〉. 表7 以〈l3〉为首的频繁序列及后缀数据库 Step 6 扫描以〈l3,l6〉为前缀的后缀数据库,以新的前缀〈l3,l6,l7〉来构造相应的后缀数据库.以〈l3,l6,l7〉为前缀的后缀数据库中,首项〈l5〉和〈l4〉都不满足支持度计数,将对应的序列〈l5〉和〈l4,l2,l1,l5〉从后缀数据库中删除,后缀数据库为空,停止对〈l3,l6,l7〉的扩展.即以〈l3〉为首的频繁序列为〈l3〉、〈l3,l6〉和〈l3,l6,l7〉. 通过和2.2.1节中PrefixSpan算法挖掘的结果对比可以发现,Im_PrefixSpan算法挖掘出的频繁序列更连续、更简洁. 本文实验是在python 3.7.2版本、Intel Core i5 2.5 GHz 和4GB内存的Windows 10实验环境下完成的.从携程旅行网站(https://www.ctrip.com/)爬取了与云南省旅游相关的 42 639 条游记,每条游记包括旅游的时间、旅行时长、人均花费和人物类型等属性.因为本文考虑的是城市级别的旅游路线,所以对于挖掘到的结果进行预处理,将游记中的地点映射到城市层面上,得到云南省的16个城市分别为昆明、大理、保山、丽江、德宏、楚雄、西双版纳、文山、曲靖、怒江、迪庆、红河、玉溪、普洱、昭通和临沧.删除了路线中城市数目少于2的路线,最终获取到 7 468 条不同的旅游轨迹数据.实验数据示例如表8所示. 表8 实验数据示例 把Im_Prefixspan算法应用于旅行轨迹数据库(即序列数据库)后,在min_support=70的情况下,得到了107条云南省旅游热门路线.以经过昆明的4条路线为例,如图1所示,图1(a)是游客经过昆明的旅游最热门路线,这也说明了游客来云南旅行,通常会选择昆明→大理→丽江→大理→迪庆→西双版纳这条线路,经了解这条线路是旅行社已经推出的经典线路.除了图1(a)路线以外,其他三条路线也很受游客青睐.从图中可以看出,这些路线的城市间相邻且距离较近,并都包含了云南省特色景点,是便捷高效且深入了解云南特色的重要线路,可以推荐给旅行社. 图1 云南省旅游热门路线 本节,将从参数和可伸缩性两方面对算法的性能进行分析,结果如图2、图3所示. 4.3.1 参数 把Im_Prefixspan算法和PrefixSpan算法分别应用于旅行轨迹数据库中,在不改变数据集的情况下,只改变支持度阈值,得到的支持度阈值与频繁序列长度的关系如图2所示,支持度阈值与算法运行时间的关系如图3所示. 图2(a)是随着支持度阈值变化得到的频繁序列的最大长度的趋势图. 图2(b)是随着支持度阈值变化得到的频繁序列的平均长度的趋势图.从图2中可以看出,随着支持度阈值的增加,Im_Prefixspan算法和PrefixSpan算法得到频繁序列的最大长度和平均长度都随之减少.支持度阈值是划分频繁序列与不频繁序列的标准,支持度阈值的增加会导致频繁序列的数目减少,由于频繁序列挖掘是按照低阶到高阶的顺序进行工作的,因此频繁序列的最大长度和平均长度也都随之减少.在同一条件下,Im_Prefixspan算法比PrefixSpan算法得到频繁序列的最大长度和平均长度要短,这是由于Im_Prefixspan算法在连续性上对PrefixSpan算法进行改进,在统计后缀数据库中各项的支持度计数时,只对首项进行计数来判断序列是否为频繁序列,而PrefixSpan算法在统计后缀数据库中各项的支持度计数时,要扫描后缀数据库中的每一项来统计后缀数据库中各项的支持度计数,所以Im_Prefixspan算法相对于PrefixSpan算法剪掉了一部分不连续序列,从而导致Im_Prefixspan算法比PrefixSpan算法频繁序列的最大长度和平均长度要短. 图3是随着支持度阈值的变化得到的算法运行时间趋势图.从图3中可以看出随着支持度阈值的增加,Im_Prefixspan算法和PrefixSpan算法的运行时间都随之减少.原因是支持度阈值的增加会导致频繁序列的数目减少,构造和搜索后缀数据库的时间都会变少. 在同一条件下, Im_Prefixspan算法比PrefixSpan算法的运行时间要少,这是由于Im_Prefixspan算法在统计后缀数据库中各项的支持度计数时,只对首项进行计数来判断序列是否为频繁序列,而PrefixSpan算法在统计后缀数据库中各项的支持度计数时,要扫描后缀数据库中的每一项来统计后缀数据库中各项的支持度计数,从而导致Im_Prefixspan算法比PrefixSpan算法的运行时间要少. 图2 支持度阈值与频繁序列的最大、平均长度的关系 图3 支持度阈值与算法运行时间的关系 4.3.2 可伸缩性 对旅行轨迹数据库进行处理,将 7 468 条序列按时间顺序进行排列,删除距今时间最远的序列,得到前 7 000 条序列,在固定阈值min_support=70的情况下,把Im_Prefixspan算法和PrefixSpan算法分别应用于旅行轨迹数据库中,得到的序列数据库规模、最长序列长度与算法运行时间的关系如图4,城市数目与算法运行时间的关系图5所示. 图4 序列数据库规模、最大序列长度与算法运行时间的关系 图5 城市数目与算法运行时间的关系 图4(a)是随着序列数据库规模的变化得到的算法运行时间趋势图.序列数据库规模的变化是通过对 7 000 条序列以 1 000 条为步长,依次删除距今时间最远的序列得到的.从图4(a)中可以看出,随着序列数据库规模的增加,Im_Prefixspan算法和PrefixSpan算法运行时间都增长很快.原因是序列数据库规模的增加,导致扫描序列数据库和构建、扫描后缀数据库的时间较长. 图4(b)是随着序列数据库中最大序列长度的变化得到的算法运行时间趋势图.从图4(b)中可以看出随着序列长度的增加,Im_Prefixspan算法和PrefixSpan算法运行时间增加的都特别快.原因是随着序列的最大长度的增加,增大了扫描序列数据库的时间,以及构建后缀数据库的次数,比如最大序列长度为13时,最多需要构建从第1层到第12层的后缀数据库.由图2(a)可知序列在阈值min_support=7时,Im_Prefixspan算法得到频繁序列的最大长度是13,所以本实验选择长度为13以内的序列来测试序列的最大长度与算法运行时间的关系,即将序列数据库中序列长度超过13的部分删除,通过对 7 000 条序列从长度13开始以1为步长,依次删除来进行测试. 图5是随着城市数目的变化得到的算法运行时间趋势图.从图5中可以看出随着城市数目的增加,Im_Prefixspan算法和PrefixSpan算法的性能都有下降.原因是随着城市数目的增加,创建的后缀数据库的数目也随之增加,比如对于两个城市a,b,c,只需要创建关于序列a,b,c为首的后缀数据库.城市数目按照昆明、大理、保山、丽江、德宏、楚雄、西双版纳、文山、曲靖、怒江、迪庆、红河、玉溪、普洱、昭通和临沧的顺序进行处理,城市数目是2时,只保留序列数据库中的城市昆明、大理,其他城市全部删除,其他数目同理,从而得到如图5所示随着城市数目变化的算法性能趋势图. 根据实验可得,在同等条件下Im_Prefixspan算法比PrefixSpan算法的运行时间都要少,原理在上节“图3 支持度阈值与算法运行时间的关系”中已做解释. 针对旅游热门路线的问题,考虑游客在旅游过程中对路线连贯的需要,改进了PrefixSpan算法,弥补了PrefixSpan算法应用在旅游路线上连续性不足的问题,并提高了算法的效率.通过示例可以看出,文中提出的算法较原算法在处理旅游热门路线问题上具有更好的连续性和简洁性. 本文的工作还可以从下面2个角度进行深入研究.第1,仅对城市旅游路线进行挖掘,以后的研究可以进一步考虑景点或者国家级别的热门旅游路线推荐.第2,在推荐热门旅游路线上主要考虑了连续性,在以后的研究中可以考虑增加对旅游时长和旅游时间的约束,为游客推荐更为人性化的结果.

2.2 PrefixSpan算法的连续性问题


3 改进的PrefixSpan算法
3.1 改进的PrefixSpan算法描述
3.2 改进的PrefixSpan算法实例
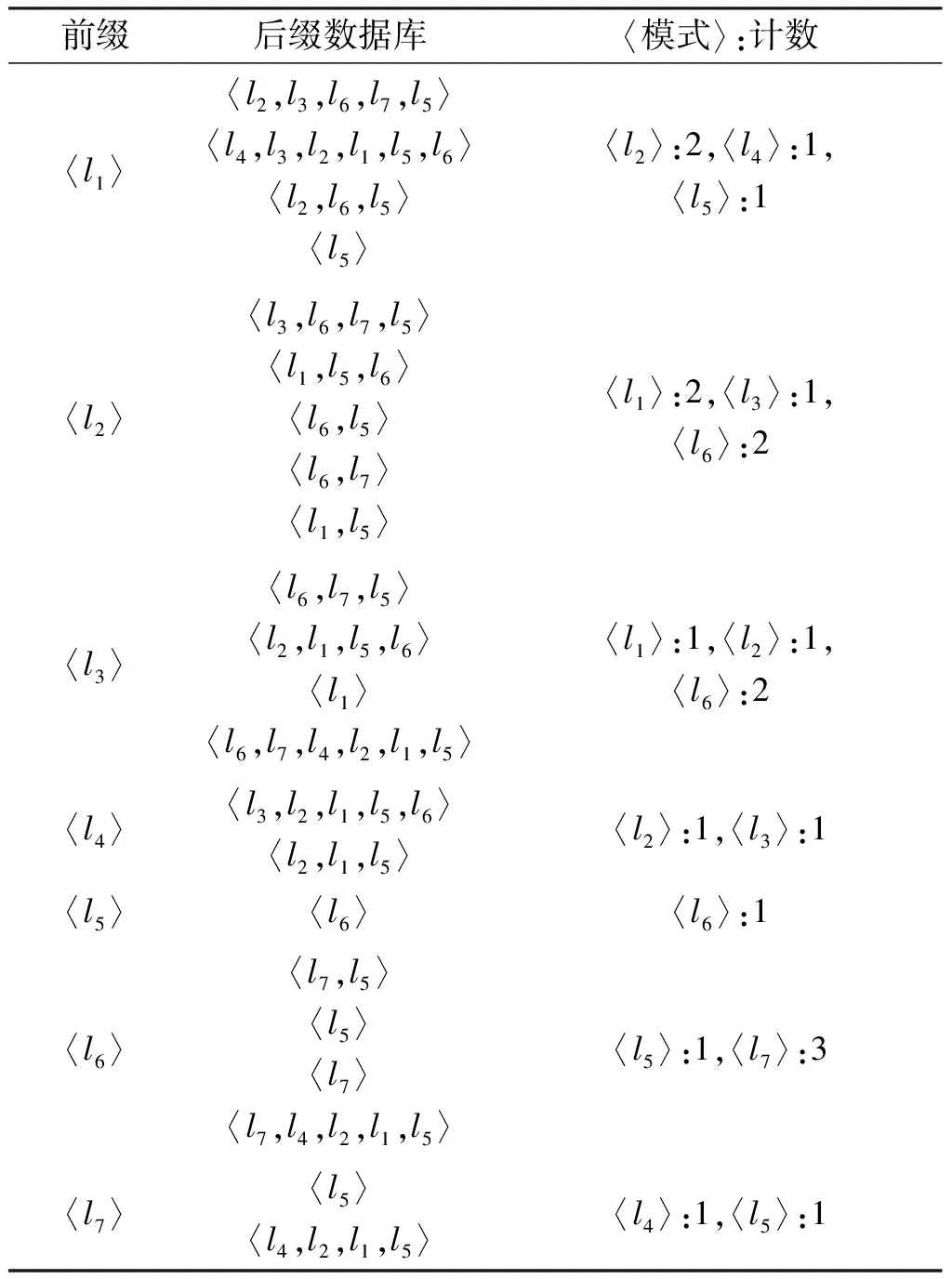

4 实验结果及性能分析
4.1 实验数据

4.2 实验效果分析
4.3 实验性能分析


5 结语
