基于复杂网络的电力信息相依网络鲁棒性研究

赵 莹，李 琰，徐天奇

(云南民族大学 电气信息工程学院，云南 昆明 650500)

近年来，我国建设以特高压电网为骨干网架、各电压等级电网协调发展的坚强型智能电网，随着智能电网的不断发展，传统电网已经向电力信息相依网络过渡，然而相依网络加剧了网络的复杂度，给网络带来的新的挑战.具体地，相依网络中单一故障可能会引起级联故障，从而造成大规模的停电事故，如2003年美国东北部发生了严重的级联故障[1]，导致发生停电事故.为保证电力系统在大规模互联网络中能安全经济的运行，相依网络鲁棒性的研究成为智能电网的一个挑战，为了解决这一问题，本文提出根据复杂网络拓扑结构特征研究相依网络的鲁棒性.

以往都是基于复杂网络理论来研究单层电力网络，直到Buldyrev等提出相依网络模型并研究他们所提出的相依网络模型[2]，复杂网络研究的对象从单网转向了相依网络.因此，许多学者开始从相依网络的级联故障、攻击模式、拓扑结构等方面研究网络性能，文献[3-4]提出了基于边移除研究智能电网鲁棒性，文献[5]根据电网静态结构分析单层网络鲁棒性，文献[6]建立电网模型并根据电气介数研究脆弱性，文献[7]通过攻击负载节点比较电力信息相互依存网络和单层网络的鲁棒性，文献[8]从动态和静态两个方面研究相依网络的鲁棒性，文献[9,15]建立相依网络模型，从网络级联故障角度出发，研究相依网络结构脆弱性.

上述研究建立的是无权网络模型，因此本文从复杂相依网络的角度出发，将电网层和通信网层抽象为由点和边组成的加权网络[17]，其中通信网节点给电网节点传输控制信息，保证电网的正常运行，电网节点给通信网节点供电确保控制信息的正常传输.此外上述研究没有说明选择哪种故障模式研究网络性能.因此本文根据五种故障模式分析单层电网鲁棒性，并选择合适的故障模式分析相依网络鲁棒性.

1 网络参数和指标

1.1 复杂网络的特征参数

1) 度数k：节点度数定义为与该节点连接的边数；

2) 介数Bi(节点介数和边的介数)：边介数通过某一条边的最短路径条数定义；节点介数通过经过某节点的最短路径条数定义.

3) 度分布：是指在网络中随机选择一个节点其度数为k的概率P(k).

1.2 鲁棒性评估指标

1.2.1 单层电网鲁棒性评估指标

网络发生故障可能会出现分裂，这时系统中会存在孤立的节点或互相不连通的子网络，原本连通的节点现在无法实现网络传输.可见最大连通度对网络的性能有很大的影响，尤其是电力网络，因为只有连通才能进行电能的传输.因此用最大连通度[16]指标来评估单层电网鲁棒性，其表达式为：

(1)

其中N1表示故障发生后，所有子图中最大簇的总节点数，N表示故障发生前网络的总节点数，S越大，表明网络的鲁棒性越好.

1.2.2 相依网络鲁棒性评估指标

相依网络中电力网络和通信网络相互依存，因此电网或通信网任意一个网络中的节点或边发生故障都会影响电力网络的最大连通度.用网络故障前后电网的最大连通度的比例作为电网的有效区域[17-19]来评估电网的鲁棒性，其表达式为：

(2)

其中S1为发生故障后网络的最大连通度，S为发生故障前网络的最大连通度.

2 单层电网模型和相依网络模型

基于复杂网络理论将网络模型抽象为由节点和边组成的拓扑图，网络用G=(N,E)表示，N是图中所有节点的集合，E是图中所有边的集合；其中电网层节点是发电机、母线等，边是输电线路，变电站等；通信层节点是调度中心、路由等，边是通信线路.相依网络的相互依存[20]方式有“一一对应”、“一对多”、“多对多”等.

文中考虑一一对应相依方式，电网层电源节点作为通信网层通信节点并与通信节点一一对应连接，本文根据IEEE30和IEEE118节点系统建立单层网络和相依网络模型，网络模型数据见表1.

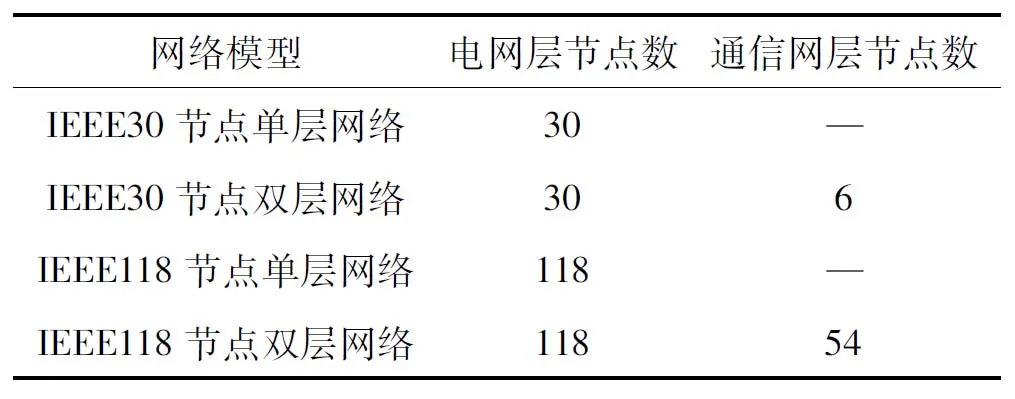
表1 网络数据

2.1 建立拓扑模型

这里以IEEE30节点电气接线数据为例，建立以电抗为权值的IEEE30节点单层电网见图1和双层相依网络的拓扑模型如图2：

图1 IEEE30节点系统单层网络拓扑图

图2 IEEE30节点系统双层网络拓扑图

2.2 相依网络电网侧网络特征

由于复杂网络的节点度分布近似于泊松分布，为了说明基于复杂网络特征可以研究相依网络鲁棒性，我们分析相依网络单侧电网的节点度分布，图3分别是IEEE30和IEEE118节点系统相依网络的单侧电网节点度分布，可见图中度较高节点分别概率较小，其余节点度分布比较均匀，符合泊松分布，这为基于复杂网络研究鲁棒性提供理论依据.

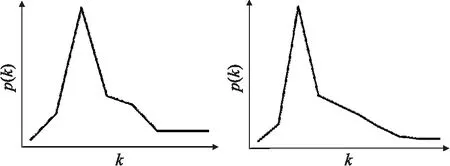
图3 节点度分布曲线

3 鲁棒性分析

建立网络模型之后，基于复杂网络结构特征，考虑网络结构的所有特征，分别从以下5种故障模式分析单层电网鲁棒性[21-22]：

(1)移除高度数节点

(2)移除高介数节点

(3)移除随机节点

(4)移除随机边

(5)移除高介数边

3.1 单层网络鲁棒性

IEEE30系统有30个节点41条边，我们假设移除30%的故障节点或边.首先基于复杂网络理论，调用度数和介数算法，得到高度数节点、高介数节点和高介数边，接着按照不同的故障模式移除节点或边，最后根据指标(1)计算每移除一个节点(一条边)的网络最大连通度.图4为5种故障模式下，移除30%节点或边单层电网最大连通度.

图4 电网最大连通度曲线

图中可以看出，移除30%的高度数和高介数的节点后网络的最大连通度要远低于移除30%的随机节点后网络的最大连通度；移除30%高介数边后的网络最大连通度低于移除30%随机边后网络的最大连通度.说明高度数节点、高介数节点和高介数边发生故障对网络鲁棒性的影响更大，且高度数和高介数节点对网络鲁棒性的影响程度基本相同.

因此本文选择移除高度数节点和移除高介数边两种故障模式分析相依网络的了鲁棒性.

3.2 标准算例系统相依网络鲁棒性分析

第2节中建立了一一对应相依网络模型，该模型直观的展现了电力网络和通信网络之间的相互依存关系.就该模型而言，电力节点给与之一一对应的通信节点供电，反过来通信节点采集电力节点的信息，由于电力网各节点之间存在联系，通信网各节点之间也有联系，就单个网络而言，他们自身网络内部存在能量传输和信息传递.

而就相依网络而言，如果通信网络的任意边发生故障，那么连接这条边的2个节点之间就失去了联系，与这2个节点相依的电力网的节点也有可能出现故障，这种情况就是通信网故障引起的电力网故障；反之，电力网节点或边发生故障有可能会使通信网对电网的控制就会出现差错，从而影响电网性能，这种情况就是电力网故障引起通信网对电力网故障的加深[25-28].

与单层网络不同，相依网络笔者倾向于研究网络耦合对电力系统性能的影响.因此基于电网有效区域评估指标，按上一小节中选择出的移除高数节点和高介数边两种故障模式，分析相依网络的鲁棒性：

3.2.1 移除高度数节点故障模式鲁棒性分析

基于电网有效区域指标，计算移除高度数节点节点数相同时，IEEE30和IEEE118节点单层电网和相依网络的电网有效区域，结果见图5.

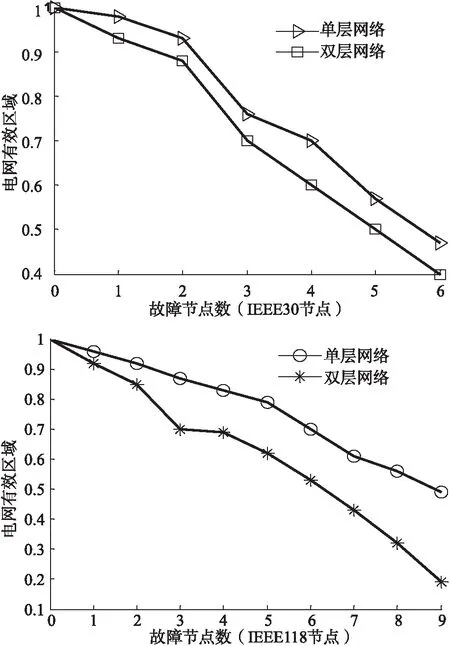
图5 移除高度数节点电网有效区域

比较图中的单层网络和相依网络电网有效区域曲线，可以看出相依网络发生故障的电网有效区域曲线下降程度高于单层网络.

具体地，IEEE30系统单层网络和相依网络都有6个节点发生故障时，单层网络节点发生故障后的电网有效区域高于相依网络节点发生故障后的电网有效区域；同样IEEE118系统中相依网络有9个节点发生故障后电网有效区域不到20%，而单层网络发生故障后电网的有效区域差不多还有50%.说明重要节点发生故障后相依网络的鲁棒性低于单层电网鲁棒性.

3.2.2 移除高介数边故障模式鲁棒性分析

同理，用移除高介数边故障模式的电网有效区域见图6.可以看出相依网络中发生故障电网有效区域曲线下降程度高于单层网络中发生故障有效区域曲线.

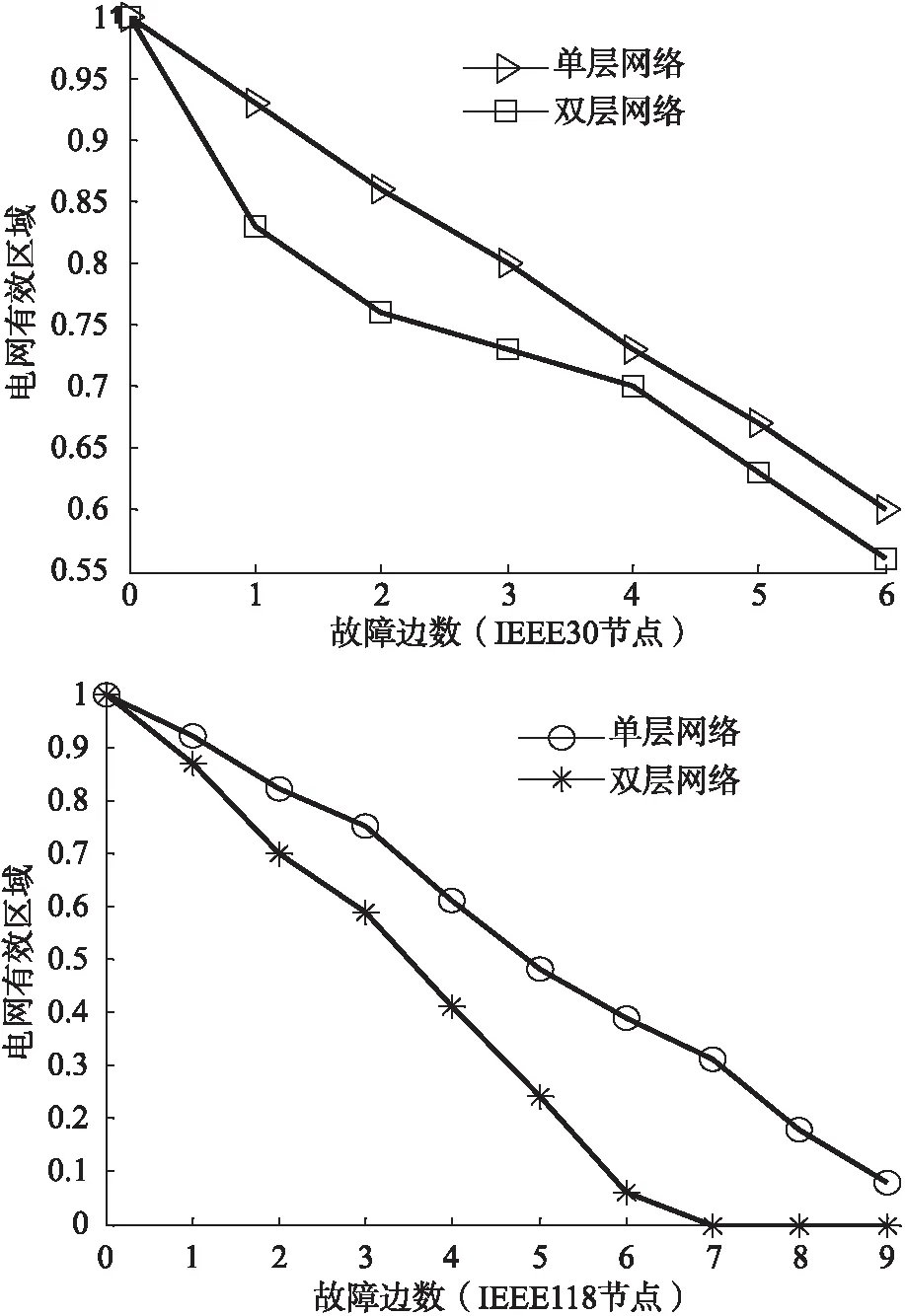
图6 移除高介数边电网有效区域

具体地，IEEE30系统相依网络中6条边发生故障后电网有效区域低于单层电网6条边发生故障后的电网有效区域；IEEE118系统相依网络中9边发生故障后的电网有效区域0，此时电网已经大面积的崩溃；而单层电网中有9条边发生故障后电网有效区域大约还有30%.说明发生高介数边发生故障后相依网络鲁棒性低于单层电网鲁棒性，这一结论和以高度数节点发生故障分析相依网络鲁棒性的结论一致.

因此根据电网有效区域指标分别以高度数节点和高介数边发生故障的故障模式对比分析IEEE30、IEEE118节点单层网络和相依网络的鲁棒性，得出相依网络鲁棒性要比单层电网鲁棒性差.

3.3 模拟实际网络的相依网络鲁棒性分析

上一节基于复杂网络提出合理的故障模式分析了相依网络的鲁棒性，并用IEEE30和IEEE118节点标准算例系统进行验证.而本节文中用模拟实际电网进行验证.

同理基于复杂网络理论根据南方电网接线拓扑图，建立相依网络模型并分析网络结构特征，根据指标(2)分析相依网络的鲁棒性.由于实际电网中线路发生故障的概率较大，因此这里根据移除高介数边和移除随机边2种故障模式分析相依网络的鲁棒性.移除故障边之后网络的电网有效区域曲线见图7.

图7 模拟实际相依网络电网有效区域

图中可以看出，相同故障模式下，单层电网的有效区域曲线下降程度高于相依网络.具体地，9条随机边发生故障后单层电网的有效区域高于双层相依网络的有效区域；9条高介数边发生故障后，双层相依网络的有效区域不到30%，而单层电网有效区域大约还有55%.所以，在2种边故障模式下模拟实际相依网络电网的边发生故障之后有效区域大幅度降低，说明相依网络对实际电网鲁棒性具有较大的影响，即模拟的实际相依网络鲁棒性也低于单层电网鲁棒性.

4 结语

基于复杂网络理论建立IEEE30、IEEE118节点系统复杂网络拓扑模型，其中包括单层电网模型和双层相依网络模型.为了研究相依网络的鲁棒性，从单层电网出发，提出最大连通度指标以5种故障模式分析单层网络鲁棒性，在此基础上选择有效的故障模式，基于电网有效区域指标评估相依网络鲁棒性.此外还建立模拟实际电网的相依网络，并根据实际电网故障多发情况，以移除边故障模式研究相依网络鲁棒性.研究结果表明，标准算例系统相依网络在高度数节点和高介数边故障模式下，相依网络的鲁棒性都要弱于单层电网；而模拟实际相依网络在随机边和高介数边故障模式下也表现出相依网络鲁棒性差的特点，可见相依网络确实降低了电网的鲁棒性.上述结果为今后研究提高相依网络鲁棒性工作奠定理论依据.