一种基于后缀排序快速实现Burrows-Wheeler变换的方法

李 冰 龙冰洁刘 勇

(东南大学集成电路学院 南京 210000)

一种基于后缀排序快速实现Burrows-Wheeler变换的方法

李 冰 龙冰洁*刘 勇

(东南大学集成电路学院 南京 210000)

近年来，Bzip2压缩算法凭借其在压缩率方面的优势，得到了越来越多的应用，Bzip2的核心算法是Burrows-Wheeler变换(BWT), BWT能有效的将数据中相同的字符聚集到一起，为进一步压缩创造条件。在硬件实现BWT时，常用的基于后缀排序的算法能有效克服BWT消耗存储资源大的问题，该文对基于后缀排序实现BWT的方法进行了详细分析，并且在此基础上提出了一种快速实现BWT的方法后缀段算法。仿真结果表明后缀段算法在处理速度上比传统的基于后缀排序的算法有很大的提高。

信号处理；数据压缩；Bzip2；Burrows-Wheeler变换；后缀排序

1 引言

数据压缩在信息技术中占有很重要的地位，传统的LZ系列和ZIP系列压缩算法利用了数据内部的重复性，对数据重复性进行记录，然后对数据进行编码处理，从而得到压缩数据。这些压缩算法的压缩率在一定程度上取决于数据内部的重复性。Bzip2与这些传统的算法不同，Bzip2的核心变换算法Burrow-Wheeler 变换(Burrows-Wheeler Transform, BWT)是一种不依赖于数据内部重复性的变换方法，它能将数据内部相同的字符聚集到一起，这使得Bzip2的压缩率基本不会受到数据内部重复性的影响，Bzip2压缩数据主要由游程编码(Run-Length Encoding, RLE), BWT，前移变换(Move-To-Front, MTF)以及霍夫曼(Huffman)编码4个步骤组成，Bzip2的压缩性能比其它传统的压缩算法都要高，但是耗费的压缩时间比较长[1-4]。

Bzip2压缩数据过程中耗时最多的是BWT，快速实现BWT能有效地减少Bzip2压缩数据的时间。BWT由Burrows和Wheeler在1994年提出[5]，这种算法的核心思想是对字符串轮转后得到的字符矩阵进行排序和变换，得到的结果序列中相同的字符在很大程度上聚集到了一起，这样的特性很适合使用通用的统计压缩模型(Huffman编码、PPM算法等)进行压缩，并得到理想的压缩率[5-7]。BWT原始算法是通过矩阵完成的，需要占用大量存储资源，交织(Weavesort, WS)编码算法的出现解决了这个问题，但是这种算法处理的速度太慢[8-11]，基于后缀排序的算法(Suffix sorting)比WS算法在速度上提高了很多，其中双向搜索算法(Bi-directional search)进一步提高了处理速度[12-16]。本文通过对基于后缀排序实现BWT算法的研究，结合后缀排序以及BWT自身的特点，提出了一种快速实现BWT的算法，称其为后缀段算法，仿真结果证实了这种算法能在存储资源消耗与双向搜索算法基本相当的情况下大大减少BWT的时间。

2 BWT与后缀排序

对于一个包含N字节的字符串S，对其进行BWT由3个步骤组成：

步骤 1 构造一个N×N矩阵M(M中的每一行分别是S左移0,1,…,n-1个字符)；

步骤 2 对矩阵M行向量按字典顺序进行升序排序，得到新的矩阵MT；

步骤3 输出MT中最后一列(记为L)以及原字符串S在MT中的行号index。

以abraca为例，其BWT变换过程如图1所示。

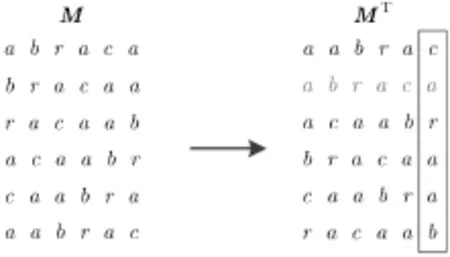
图1 BWT实例

abraca的BWT结果L=caraab , index = 1是用于进行BWT反变换的。BWT之后，数据长度并没用缩短，但相同字符很大程度上被排列到了一起。

对于字符串S:X1X2…XN，将它的子字符串XiXi+1…XN称为后缀Si，后缀之间存在着大小关系，假设有后缀Xi与Xj，定义其大小关系为：

(1)如果Xi＞Xj，则Si＞Sj；

(2)如果Xi＜Xj，则Si＜Sj；

(3)如果Xi=Xj，则继续比较Si+1和Sj+1，比较规则同(1)和(2)。

对于字符串S:X1X2…XN，在其后面添加一个$，得到S′:X1X2…XN$其中$ 需要满足条件$>Xt,t=1,2,…,N ，即$要比S中所有字符的字典序都要大，将S′的所有后缀进行升序排序，同样以abraca为例，首先在其后面添加一个$ ，这样这个字符串就有7个后缀，分别是S1:abraca$,S2: braca$,S3:raca$,S4:aca$,S5:ca$,S6:a$,S7:$根据后缀大小的比较规则，这些后缀的升序排列结果为S1S4S6S2S5S3S7，现在用每个后缀在S′中的前一个字符代替，得到X7X3X5X1X4X2X6，即$rcaaba，同样，参照图1所示的方法对S′进行BWT，可以发现其BWT结果也是$rcaaba，也就是说只要进行BWT的字符串满足最后一个字符的字典序比其它出现在字符串中的字符的字典序都大这个条件，那么就可以用后缀排序来得到它的BWT结果，实际上满足这个条件的字符串很少，但是一般在读入数据流的时候，都会默认添加一个文件结束符(End of File, EOF)，而EOF恰好是满足这个条件的，所以后缀排序的时候带上EOF就可以了。

对于一个字符串S:X1X2…XN对其后缀进行排序，从第1个后缀S1(S)开始处理，直到最后一个后缀SN(XN)，处理后缀Si相当于是都在S1S2…Si-1的升序排列集合中插入Si，用Ti-1来表示这个升序排列集合，将这样的集合称为后缀链表。当所有后缀完成排序后，得到后缀链表TN，将TN中的所有后缀用它在S中的前一个字符(图1中矩阵MT的最后一列)替换，即后缀用字符替换(S1用XN替换)，这样得到的字符串就是S的BWT结果，这就是后缀排序实现BWT的原理，也是基于后缀排序实现BWT的基本算法。

在后缀排序中将后缀Si插入到后缀链表Ti-1的过程中，需要将Si与Ti-1中所有后缀进行比较，从而确定Si在Ti-1中的位置，称这个过程为搜索。以降序搜索为例，当Ti-1中所包含的后缀很多，并且Si比Ti-1中绝大多数后缀都要小的时候，搜索过程耗费的时间是很长的，这种情况下采用升序搜索就能很快确定Si在后缀链表中的位置，于是基于后缀排序实现BWT的双向搜索算法也很自然地被提出，就是在后缀链表中升序搜索和降序搜索同时进行，只有有一个方向上找到Si对应的位置，即停止搜索，并插入Si，然后更新相应的信息。但是当数据块很大，处理过程中Ti-1包含的后缀越来越多，而且Si处于Ti-1的中间位置的时候，即使采用双向搜索算法，耗费的时间也是很长的。

3 后缀段算法

仔细分析一下后缀排序的特点，可以发现有很多特点是可以利用的。

对于字符串S，定义集合Pi:{Sj:j＜i,Xi= Xj,Si+1＜Sj+1}，它表示当前后缀链表Ti-1中首字符与Si的首字符Xi相同并且比Si小的所有后缀集合，在插入Si的过程中会出现以下3种情况：

(1)Ti-1中存在以Xi为首字符的后缀Si，并且也满足Xj=Xi, Sj+1＜Si+1，这时Pi不是空集；

(2)Ti-1中存在以Xi为首字符的后缀Si，但是不满足Xj=Xi, Sj+1＜Si+1，这时Pi是空集；

(3)Ti-1中不存在以Xi为首字符的后缀，这时Pi也是空集。

以降序搜索为例，在后缀排序过程中，情况(1)出现的可能性最大，出现情况(1)时，需要在Pi中搜索并插入Si；对于情况(2)和情况(3)，需要有更进一步的分析，参照双向搜索算法的原理以及集合Pi，同样可以定义集合Pi:{Sj:j＜i,Xi=Xj,Si+1＞Sj+1}，它表示当前后缀链表Ti-1中首字符与Si的首字符Xi相同并且比Si大的所有后缀集合，出现情况(2)时，检测Qi是否为空集，如果Qi不是空集，则在Qi中搜索并插入Si。

假设Pi和Qi中的后缀都是按照升序排列的，定义集合Ri:{Pi,Qi}，表示Ti-1中首字符与后缀Si的首字符相同的所有后缀的集合，称其为后缀段，并且将Si的首字符Xi称为后缀段Ri的段首字符。显然，根据后缀大小的判断规则，在后缀排序的过程中，后缀链表由0～256个后缀段(假设文件是以ASCⅡ码的形式读入)按照段首字符升序排列组成。当出现情况(1)和情况(2)时，Ri不是空集，在插入后缀Si时，只要能确定以Xi为段首字符的后缀段Ri在后缀链表中的位置，接下来在Ri中搜索并插入Si就可以了。当出现情况(3)时，Ri是空集，这时需要做的就是找到段首字符与Xi距离最近的段，然后根据大小情况将Si插入到对应的位置。

通过以上分析可以知道在后缀排序过程中，有3条信息是可以利用的：(1)Ri是否已经存在于当前的后缀链表Ti-1中，这个信息可以用一个数组appear记录，appear[i]=1表示Ri已经存在于后缀链表中，appear[i]=0表示Ri还不存在；(2)当前Ri中最大的后缀max[i], max[i]里面存放的是当前Ri中最大的后缀在后缀链表中的地址；(3)当前Ri中最小的后缀min[i], min[i] 里面存放的是当前Ri中最小的后缀在后缀链表中的地址，信息(2)和(3)用于确定Ri在后缀链表中的位置。在后缀排序过程中后缀链表结构如图2所示。

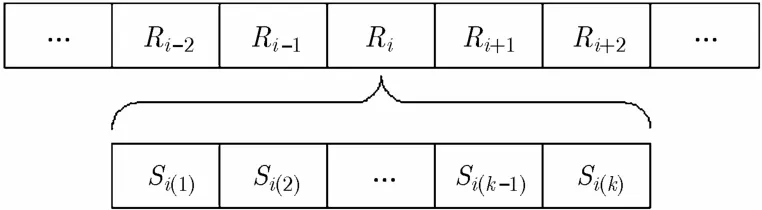
图2 后缀链表结构

综合以上对后缀排序特点的分析，可以总结出后缀段实现BWT的步骤：首先初始化后缀链表为空，接下来从后缀Si开始，一直到后缀SN，每次向后缀链表中插入一个后缀。插入后缀Si的步骤如图3所示：首先检查appear[i]的值，如果appear[i]=1，说明对应的Ri已经存在，接下来在Ri内进行双向搜索并插入Si；如果appear[i]=0，说明对应的Ri不存在，这时需要查找距离最近的后缀段，根据最近后缀段的大小确定Si所在的位置并更新后缀链表和相应信息。

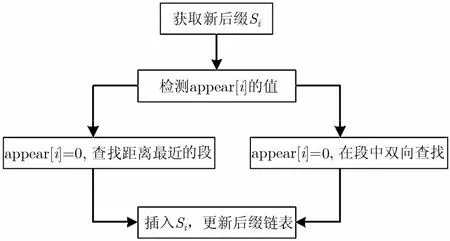
图3 插入后缀Si的流程

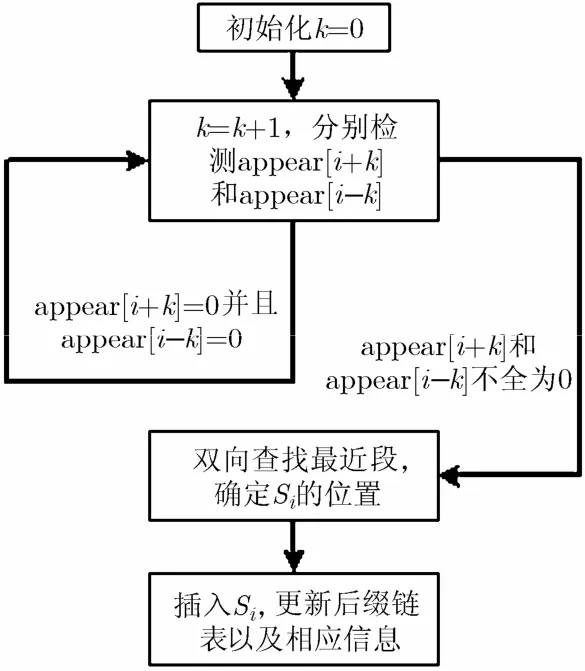
图4 查找距离最近的段流程

查找距离最近的段的步骤如图4所示。查找距离最近的段是一个双向的过程，从appear[i+1]和appear[i-1]开始依次往两边扩散，直到appear[t]的值为1，如果t＞i,Si就应该插入到段Ri中最小后缀的左边；如果t＜i,Si就应该插入到段Ri中最大后缀的右边。插入Si后，需要更新后缀链表以及相应的max[i]和min[i]的值，且令appear[i]=1。

在段Ri中双向搜索的步骤如图5所示：首先根据max[i]min[i]的值确定Ri在后缀链表中的位置，接下来从max[i]和min[i]开始依次在两个方向上往段内取相邻后缀与Si进行比较，直到确定Si在Ri中的位置，插入Si，然后更新后缀链表以及相应的max[i]和min[i]的值。

在所有后缀都已经插入到后缀链表后，把后缀链表中的所有后缀用它在S中的前一个字符替换，这就是基于后缀段实现BWT的方法。

对于硬件实现来说，存储资源是十分宝贵的资源，用硬件实现很多经典的算法时，存储资源往往成为瓶颈，一个算法是否能够很好地用硬件实现也很大程度上与其所消耗的存储资源有关，第2节曾提到用基于后缀排序的算法来实现BWT比起原始算法最大的优势就是节省了大量的存储资源，但是在变换速度上仍然显得不够，后缀段算法利用了后缀排序算法的特点，在增加了一些存储资源的情况下，大大提高了变换速度。

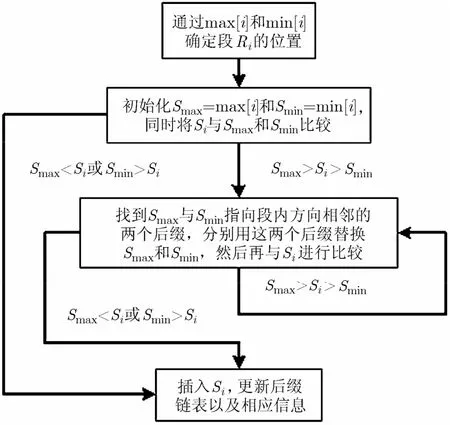
图5 在段Ri中双向搜索流程图

对于一个长度为N字节，包含T个不同的字符的字符串S，采用后缀段算法实现BWT所消耗的主要存储资源为(假设文件都是以ASCⅡ码形式读入)：

(1)位宽为8，深度为N的数组，用于存放字符串S；

(3)位宽为1，深度为256的数组，用于记录以ASCⅡ值为0～255的字符为段首字符的后缀段是否存在于后缀链表中；

4 实验结果分析

对基于后缀排序实现BWT的3种算法进行了仿真测试，测试代码是用Verilog硬件语言进行设计的，在Modelsim软件下面进行仿真。用于测试的数据是一系列长度不同的0～255的随机数，3种基于后缀排序实现BWT的算法在处理这些数据时所消耗的主要存储资源如表1所示，完成BWT的时间如表2所示。

表1给出了3种基于后缀排序实现BWT算法的存储资源，3种算法的主要消耗在于后缀链表中记录该处后缀在S中的地址，这是区分后缀的唯一标识，另外，在后缀段算法中，增加了bit的消耗，这个消耗用于记录后缀段在后缀链表中的位置，是提高排序速度必不可少的。

表1 3种算法实现BWT消耗的存储资源(bit)

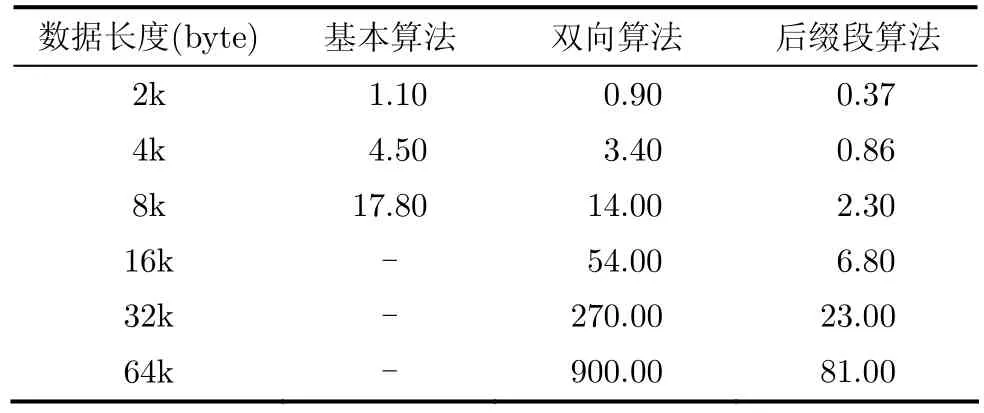
表2 3种算法完成BWT的时间(ms)

表2给出了3种基于后缀排序实现BWT算法的速度结果，表中数据长度的单位是字节，后面3列数据表示该算法处理对应大小的数据时所用的时间，单位是ms。这里由于采用基本算法处理16k字节以上大小的文件时耗时太长，所以没有给出具体数据。

从测试结果数据上可以得出一些结论：当数据的长度增加一倍时，基本算法完成后缀排序的时间大概会增加3倍；双向算法所用的时间大概也会增加3～4倍；后缀段算法所用的时间大概会增加2～3倍。在数据长度相同的情况下，双向算法完成后缀排序的时间比基本算法减少了20%，后缀段算法完成后缀排序的时间比起双向算法则有了更加明显的减少，随着数据长度的增加，后缀段算法完成后缀排序的时间比起双向算法减少的幅度也在增加，当数据长度为32k时，后缀段算法完成后缀排序所用的时间只是双向算法的十分之一不到，而且可以推测当数据长度进一步增加时，后缀段算法的优势会更加明显。

5 结束语

本文针对Bzip2压缩算法里面的BWT部分，对其原理算法进行了介绍，对基于后缀排序的BWT算法进行了详细的分析，利用后缀排序中后缀链表的组成特点提出了后缀段算法，虽然比传统的基本算法和双向搜索算法消耗更多的存储资源，但是在处理速度上得到了明显的提高。测试结果表明在处理同样长度的数据时，后缀段算法能明显减少处理时间，在数据长度从2k增加到64k时，后缀段算法与双向算法完成后缀排序所用的时间比从1:3逐渐减小到1:10不到，并且时间减少的幅度在不断增加。在后缀段中进行双向搜索的优化是进一步研究的重点。

[1] Julian Seward, Bzip2[OL]. http://en.wikipedia.org/wiki/ Bzip2, 2010.9.20

[2] Szecówka P M, and Mandrysz T. Towards hardware implementation of bzip2 data compression algorithm [C]. Proceedings of the Mixed Design of Integrated Circuits and Systems, Lodz, Polland, 2009: 337-340.

[3] Sun Wei-feng, Zhang Nan, and Mukherjee A. Dictionarybased fast transform for text compression[C]. Proceedings of the International Conference on Information Technology: Computers and Communications, Nanjing, China, 2003: 176-182.

[4] Baloul F M, Abdulah M H, and Babikir E A. ETAOSD: static dictionary-based transformation method for text compression [C]. Prioeedings of the International Conference on Computing, Electrical and Electronic Engineering, Khartoum, Sudan, 2013: 384-389.

[5] Burrows M and Wheeler D. A block-sorting lossless data compression algorithm[R]. SRC Research Report 124, Digital Systems Research Center, Palo Alto, CA, USA, 1994.

[6] Arnsvut Z. Move-to-front and inversion coding[C]. Data Compress Conference, Snowbird, USA, 2000: 193-202.

[7] Effros M. PPM performance with BWT complexity: a fast and effective data compress algorithm[J]. Proceedings of the IEEE, 2000, 88(11): 1703-1712.

[8] Martínez J, Cumplido R, and Feregrino C. A fast algorithm for making suffix arrays and for Burrows-Wheeler transformation[C]. Proceedings of the International Conference on Reconfigurable Computing and FPGAs, Puebla City, Mexico, 2005: 28-30.

[9] Kong J M, Ang L M, and Seng K P. Low-complexity two instructions set for suffix sort in Burrows-Wheeler transform[C]. Proceedings of the International Conference on Advanced Computer Science Applications and Technologies, Kuala Lumpur, Malaysia, 2012: 181-186.

[10] Arming S, Fenkhuber R, and Handl T. Data compression in hardwarethe Burrows-Wheeler approach[C]. Proceedings of the Design and Diagnostics of Electronic Circuits and Systems (DDECS), Vienna, Austria, 2010: 60-65.

[11] Grajeda V Z, Uribe C F, and Parra R C. Parallel hardware/ aoftware architecture for the BWT and LZ77 lossless data compression algorithms[J]. Computation System, 2006, 10(2): 172-188.

[12] Sadakane K. A modified Burrows-Wheeler transformation for case-insensitive search with application to suffix array compression[C]. Proceedings of the Data Compression Conference, Snowbird, USA, 1999: 29-31.

[13] Hayashi S and Taura K. Parallel and memory-efficient Burrows-Wheeler transform[C]. Proceedings of the IEEE International Conference on Big Data, Silicon Valley, USA 2013: 43-50.

[14] Zhao Zhi-heng, Yin Jian-pin, and Xiong Wei. GPU-accelerated Burrows-Wheeler transform for genomic data[C]. Proceedings of the 5th International Conference on BioMedical Engineering and Informatics, Chongqing, China, 2012: 889-892.

[15] Cheema U I and Khokhar A A. High performance architecture for computing Burrows-Wheeler transform on FPGAs[C]. Proceedings of the International Conference on Reconfigurable and FPGAs, Cancun, Mexico, 2013: 1-6.

[16] Baron D and Bresler Y. Antisequential suffix sorting for BWT-based sata sompression[J]. Computers, 2005, 54(4): 385-397.

李 冰： 男，1963年生，教授，博士生导师，研究方向为现场集成系统与信息专用集成电路设计、数据压缩等.

龙冰洁： 男，1988年生，硕士生，研究方向为嵌入式系统、数据压缩.

刘 勇： 男，1979年生，博士生，研究方向为集成电路设计.

A Fast Algorithm for Burrows-Wheeler Transform Using Suffix Sorting

Li Bing Long Bing-jie Liu Yong
(College of Integrated Circuit, Southeast University, Nanjing 210000, China)

Bzip2, a lossless compression algorithm, is widely used in recent years because of its high compression ratio. Burrows-Wheeler Transform (BWT) is the key factor in Bzip2. This method can gather the same symbols together. The traditional methods which are based on suffix sorting used in implement of BWT in hardware can solve the problem of memory consumption effectively. Detail analysis of BWT algorithm based on suffix sorting is given and a new methodSuffix segment method is presented in this paper. Experimental results show that the proposed method can much decrease BWT time consumption without increasing memory consumption much.

Information processing; Data compress; Bzip2; Burrows-Wheeler Transform (BWT); Suffix sorting

TN492

A

1009-5896(2015)02-0504-05

10.11999/JEIT140232

2014-02-24收到，2014-07-17改回

十二五国家科技支撑计划(2013BAJ05B03)资助课题

*通信作者：龙冰洁 longbj1107@sinacom