多进口旋流器流场特征及分离性能
2022-02-12张悦刊葛江波刘培坤杨兴华
张悦刊,葛江波,刘培坤,杨兴华
(山东科技大学机械电子工程学院,山东 青岛 266590)
旋流器作为一种高效固液分离设备,凭借其操作简单、占地面积小、维修费用低等优点,广泛应用于煤矿、石油、化工、环保等领域。但传统旋流器分离效率低等缺陷制约了旋流分离技术在工程领域的进一步应用。因此,改善旋流器结构,提高其分离性能势在必行。而进口结构是影响旋流流场初始流态、干预旋流分离效果的重要因素。通过优化旋流器进口结构,提前干预流体运行状态和流场分布,是提高旋流器分离效率的一种有效方法。
文献[7−8]研究发现,合适的旋流器进口宽度可以降低分离粒度,进而实现精细分离。Fan 等通过粒子图像测速(PIV)技术测量不同入口倾角对分离效率的影响,发现入口倾角为30°时分离性能最高。Yoshida等通过实验对比了传统旋流器和螺旋进口旋流器的分离性能,发现螺旋进口旋流器分离效率较传统型式有明显提高。Zhang 等采用数值模拟方法,研究了不同曲率的弧形进口对旋流流场的影响,研究发现曲率较小的弧形进口旋流器可以抑制溢流跑粗现象,进一步提升了分离精度。Li等通过数值模拟方法对比分析了渐开线和螺旋线进口旋流器的差异,结果表明:螺旋线进口型旋流器既能抑制颗粒错位,又能降低能量损耗。
旋流器进口数量对旋流器流场稳定性、分离效率同样具有重要作用。对称双进口旋流器流场具有较好的稳定性,多用于油水分离领域。Liu等、Hwang等对多进口旋流器进行了模拟研究,均认为在相同工况下,增加进口数量可以提升旋流器切向速度,增强离散相离心力,进而优化分离效率。Winfield 等采用数值模拟方法分析了单、三进口旋流器流场特征,发现三进口旋流器可以在低入口速度工况下提供稳定的旋流流场,以提升分离精度。
为了进一步研究进口数量对旋流器流场性能与分离效率的影响,本文在不改变总体进料流量的前提下,将单进口旋流器改为双进口、三进口、四进口旋流器,采用数值模拟方法研究进口数量对旋流器流场特征及分离性能的影响规律,以期为旋流器在工程领域的进一步推广应用提供理论支撑。
1 数学模型与验证
1.1 结构模型与网格划分
单进口旋流器结构如图1(a)所示,相关结构参数见表1,多进口旋流器具体结构如图2所示。
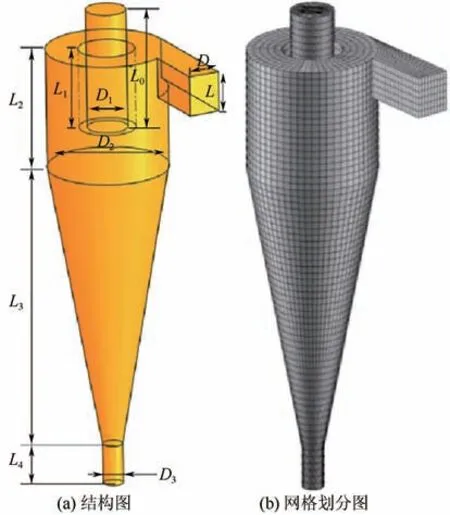
图1 单进口旋流器结构与网格划分
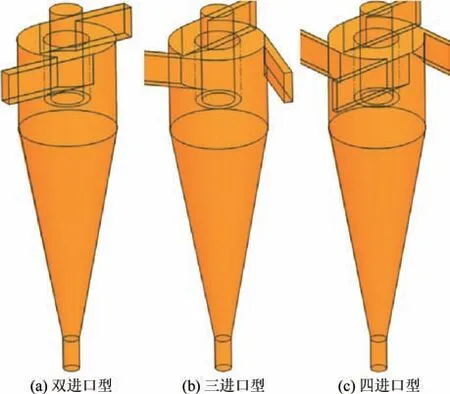
图2 多进口旋流器结构
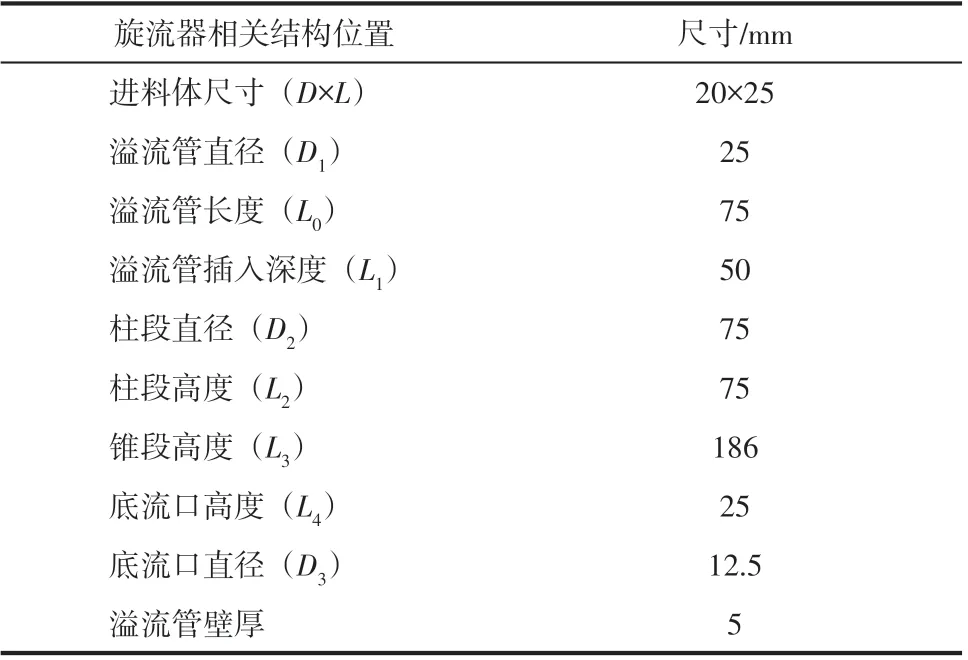
表1 旋流器相关结构参数
使用ICEM18.0 软件对旋流器流场进行网格划分,如图1(b)所示。网格数量既影响模型预测结果的准确性,又决定模型计算时间成本。因此,对旋流器模型进行网格独立性验证,确定合适的模型网格数量是必要的。将单进口旋流器流场模型划分网格数分别为27295、50925、70458、118073,进行网格独立性验证。选取旋流器轴向位置=95mm 处进行切向速度对比,从图3 可以看出,网格数在50000以上时,切向速度基本一致。综合考虑模拟结果准确性和模型计算时间成本,本文单进口旋流器流场网格数量选用50925。

图3 网格独立性验证
1.2 数学模型
VOF模型通过求解单一相动量方程[式(1)],捕捉网格中的流体体积分数,从而实现对空气柱的捕捉。

式中,α为水相体积分数,其值介于0~1 之间;v为相方向速度;、x分别为时间、位置长度。
RSM 模型考虑湍流各项异性假设,对复杂流场的预测精度较高,可以较准确预测旋流器流场特性,并通过雷诺应力输运方程[式(2)]封闭雷诺平均N−S方程进行求解。

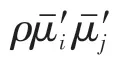
Mixture 模型作为简化的多相流模型,通过计算混合项动量方程[式(3)]、连续性方程[式(4)]可以在短时间内完成对离散相的预测。
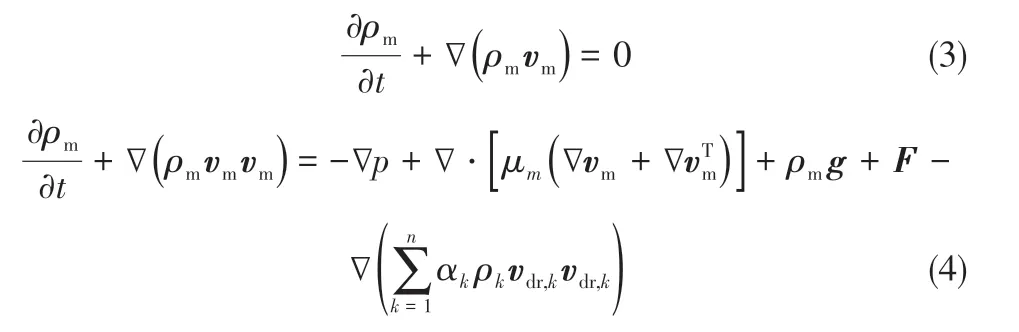
式中,为混合相密度;为混合相平均速度;为压力;为重力加速度;为体积力;αρ为第相黏度;为第相漂移速度。
DPM模型是追踪低浓度颗粒运动的有效方法,通过式(5)计算颗粒运动特性,实现对离散相运动轨迹的预测。

式中,u、ρ分别为第相颗粒速度、密度;为颗粒松弛时间;为流体速度;为附加力。
1.3 模拟参数设置
文中使用VOF模型、Mixture模型和DPM模型分别对旋流流场、离散相分离效率和颗粒轨迹进行预测,所用模型均为Fluent18.0商用软件中标准模型。模型入口均为Velocity−inlet,出口均为Pressure−out。压力−速度耦合方式采用Simple,压力离散方法采用Presto,其他离散方法使用Quick 格式。使用VOF 模型预测旋流器的流场特性,入口速度为2.28m/s,空气回流系数为1。Mixture模型使用CaCO颗粒预测离散相的分离效率,颗粒体积分数为5.4%,具体颗粒粒径分布及体积分数见表2。DPM模型入口、溢流口均为escape模式,底流口为trap模式。计算时以进出口单位时间内各相流量不平衡误差小于10作为计算收敛的依据。

表2 颗粒粒径分布及体积分数
1.4 模型验证
相关数学模型使用前需要进行模型准确性验证。Hsieh 等测量了75mm 旋流器内部流场速度,本文采用VOF 耦合RSM 模型,模拟得到了单进口旋流器流场的切向速度分布,如图4(a)所示,与Hsieh 等实验数据进行对比,两者速度结果基本一致;将Mixture模型预测结果与文献[22]的试验结果进行比较,如图4(b)所示,二者具有较高的一致性。
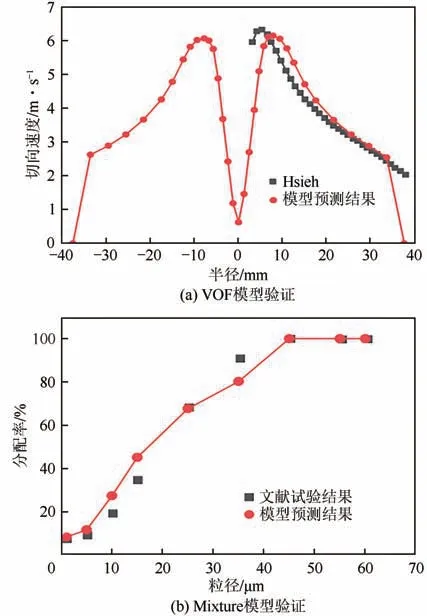
图4 模型准确性验证
2 结果与分析
旋流器结构图坐标原点设为旋流器溢流管端面中心,选取坐标轴=0时的截面为中心截面;进口横截面位置设在=30mm处,如图5所示。
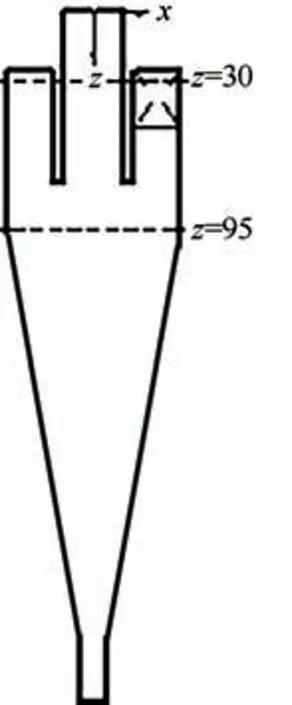
图5 旋流器中心截面位置
2.1 压力分布
图6为不同进口旋流器不同高度位置的压力分布,可以看出,当旋流器位置高度<157.5mm 时,多进口旋流器(二、三和四进口旋流器)径向压力峰值较单进口旋流器的径向压力更大。而当旋流器位置高度>157.5mm 时,4 种旋流器流场压力分布基本相同。为进一步分析流场压力变化,选取4种旋流器中心截面上高度=95mm 处径向压力进行分析,如图7所示。从定量角度分析流场径向压力变化,可以看出在旋流器器壁处,多进口旋流器压力值均大于单进口旋流器,且进口数量为偶数时,流场压力值更大。因此,增加旋流器进口数量,有利于流场径向静压力提升,从而增大颗粒径向受力,强化颗粒分离效果。

图6 不同高度静压分布云图

图7 压力分布曲线(z=95mm)
2.2 切向速度
旋流流场切向速度决定了颗粒离心力的大小,影响颗粒从内旋流到外旋流的逃逸能力。图8是不同进口旋流器不同位置高度的切向速度云图,可以看出,4种旋流器切向速度均呈现出从器壁到旋流中心先增加后降低的趋势,但是进口数量仅对旋流场=30mm 和=51mm 高度位置的切向速度大小有一定影响,表现为从单进口到四进口旋流器,进口截面处流场切向速度随进口数量的增加而增大,而随着旋流器轴向位置的变化,这种影响逐渐减小。这一现象可以通过=72mm 和=95mm 位置的切向速度云图看出。因此,可以认为进口数量仅在一定位置高度影响切向速度场变化,该影响随值增大而逐渐降低。

图8 不同位置高度的切向速度云图
2.3 轴向速度
图9 是4 种旋流器中心截面上=95mm 高度位置的轴向速度分布曲线,可以看出:旋流器中心轴向速度随进口数量的增加而增加。同时,相比于三进口旋流器,四进口旋流器轴向速度最大值略有降低,但仍大于单进口旋流器中心轴向速度。空气柱区域轴向速度的增加在一定程度上了带动了内旋流的上升,所以增加旋流器进口数量,可以提升中心区域附近的流场轴向速度,进而强化旋流器处理能力。图10是不同进口旋流器轴向零速包络面云图,图中蓝色区域为外旋流流场。由图10 可以看出,相比于单进口旋流器,多进口旋流器轴向零速包络面波动性更小,这表明增加进口数量有利于增强旋流器分离空间内矿浆运动的稳定性。
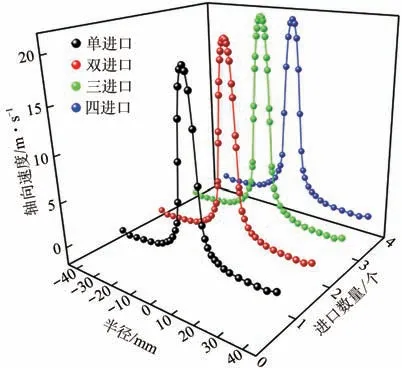
图9 轴向速度曲线分布(z=95mm)

图10 轴向零速包络面云图
2.4 空气柱
空气柱的生成是旋流器流场稳定的重要标志,且空气柱对旋流器分离性能具有重要影响。图11是不同进口结构旋流器空气柱的产生、发展、演化过程。对比空气柱形态可以发现,进口数量对稳定的空气柱形成时间有一定影响。对于多进口结构旋流器,流场运行时间均在0.6s时形成较为稳定的状态,而单进口旋流器空气柱在该时间时仍表现为偏摆非常明显的非稳定状态。为进一步分析4种旋流器对空气柱直径的影响,提取气液边界面绘制空气柱边界位置曲线,如图12所示。经对比可以发现,处于不同轴向位置的空气柱直径均有随着值的增大而减小的趋势。同时还可以发现,多进口旋流器空气柱直径总体比单进口旋流器空气柱直径略小,从而表明多进口旋流器不仅有利于流场在短时间内趋于稳定,而且由于空气柱直径较小,可以在相同的工况下有效提升旋流器的处理能力。但同时也发现,由于多进口旋流器多个进料体的叠加,使得多进口旋流器空气柱径向波动比单进口旋流器略有增加。
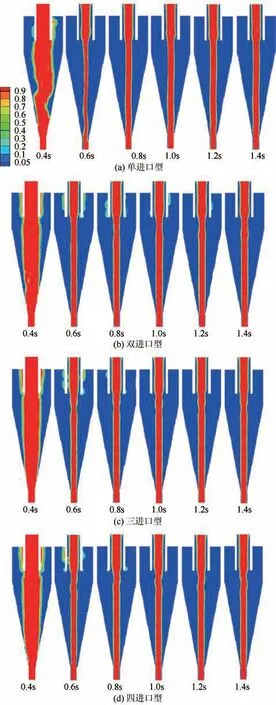
图11 空气柱形成过程

图12 空气柱边界曲线图
2.5 湍动能
湍动能对旋流器流场的稳定性、分离性能、能耗均有影响,图13 是不同进口旋流器中心截面湍动能云图。对比图13 可以发现,在主分离区内,多进口旋流器(二、三和四进口)湍动能略大于传统旋流器,而在溢流管内单进口旋流器的湍动能比其余3种旋流器大,两者作用区域不同。在主分离区域内矿浆运动产生的湍动能对矿浆分离产生影响,较大的湍动能可能引起颗粒在液体内的波动性,影响分离精度;在溢流管内空气和矿浆流动产生的湍动能会对能耗产生额外影响,较大的湍动能会带来能耗的增加。
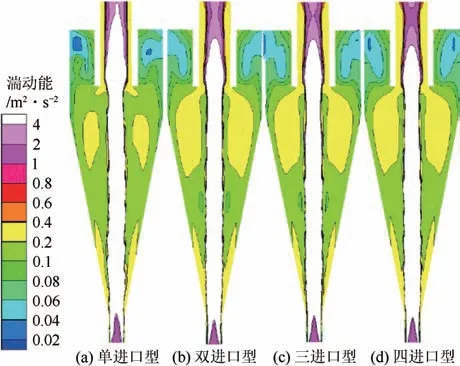
图13 湍动能云图
2.6 颗粒轨迹
通过DPM 模型追踪了不同旋流器中7.5μm 细颗粒和57.5μm 粗颗粒的运动轨迹,如图14 所示,其中图14(a)~(d)依次为单、双、三和四进口旋流器中7.5μm颗粒轨迹线,图14(e)、(f)为对应不同进口旋流器中57.5μm 颗粒轨迹线。图中可以看出,4 种进口旋流器内57.5μm 粗颗粒运动轨迹基本一致。但在相同工况下,从进口到底流口的最短分离时间分别为0.6s、0.53s、0.46s、0.416s,这表明入口数量越多,颗粒在旋流器内停留时间越短,越有利于提高粗颗粒的处理效率。而由于7.5μm颗粒粒径小,受湍流扩散影响较大,其轨迹线具有较强的随机性,很短时间内就从溢流口排出,因此入口数量对细颗粒的分离时间基本没有影响。

图14 颗粒轨迹线
2.7 分离性能
分配率是衡量旋流器分离效果的重要指标,图15 是不同进口旋流器底流分配率曲线。可以看出,当入口速度为3m/s、单进口旋流器处理粒径为50μm、57.5μm 颗粒时,底流分配率分别为81.40%、90.75%;当旋流器进口数量为二、三和四进口时,50μm 粒径颗粒的底流分配率分别达到92.00%、91.90%和90.50%,57.5μm 颗粒的底流分配率分别达到96.34%、96.34%和96.30%。相同物料条件下,只有当单进口旋流器入口速度为7.5m/s时,50μm、57.5μm 颗粒的底流分配率才能达到96%,这说明可以通过适当增加进料速度和增加进口数量来实现粗颗粒底流分配率的提升。

图15 底流分配率曲线
为了进行分离性能的全面分析,引入了分离粒度()和可能偏差()两个指标。表3 是不同进口旋流器分离粒度和可能偏差指标值。由表3可以看出,入口速度为3m/s、进口数量为二、三和四时,其均比单进口旋流器小。同时还能看出,双进口和三进口旋流器值要小于传统单进口旋流器,但进口数增加到四进口时,又出现增大趋势。
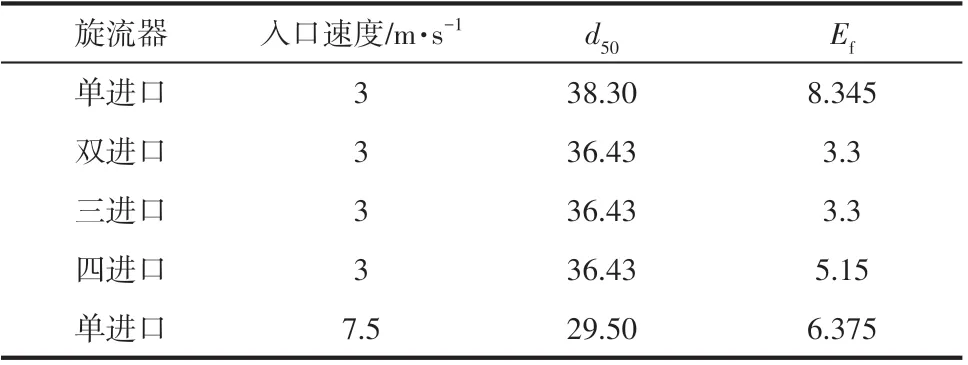
表3 分离粒度和可能偏差表
3 结论
通过对单、双、三、四进口旋流器流场特征及分离性能的对比模拟研究,得出以下结论。
(1)旋流器进口数量的改变会对旋流器流场产生影响,相比于传统旋流器,多进口旋流器可以有效增加流场径向压力和矿浆分离区域内流场的稳定性。
(2)进口数量的增加可以有效提升旋流器分离性能。在分离50μm、57.5μm粗颗粒时,多进口旋流器(二、三和四进口)的底流分配率较传统单进口旋流器分别提升了10.60%、5.59%。
(3)多进口旋流器可以减小分离粒度,同时,多进口旋流器能在较低速度入口工况下实现传统旋流器高入口速度才能完成的分级效果。
需要指出的是,尽管本文通过数值模拟方法从不同角度分析了进口数量对旋流器流场和分离性能的影响,但由于流场的复杂性,研究过程中忽略了颗粒与颗粒之间、颗粒与流体之间的相互作用的影响,因此多进口旋流器的分离性能有待进一步深入研究。
符号说明
,,,—— 分别为进料体长度、溢流管直径、柱段直径、底流口直径,mm
—— 雷诺应力输运方程中湍流扩散项,Pa/s,,=1、2、3
—— 雷诺应力输运方程分子扩散相,Pa/s,,=1、2、3
—— 分离粒度
—— 可能偏差
—— 体积力,N
G—— 雷诺应力输运方程产生相,Pa/s,,=1、2、3
—— 重力加速度,m/s
,,,,—— 分别为进料体高度、溢流管插入深度、柱段高度、锥段高度、底流口长度,mm
P—— 雷诺应力输运方程压力相,Pa/s,,=1、2、3
—— 压力,N
,—— 分别为时间和颗粒松弛时间,s
—— 第相漂移速度,m/s
v,—— 分别为水相方向速度、流体平均速度,m/s,=1、2、3
,u—— 分别为混合相平均速度、相颗粒速度和流体速度,m/s
x—— 位置长度,mm,=1、2、3
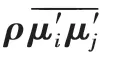
—— 水相的体积分数,%
ε—— 雷诺应力输运方程耗散相,Pa/s,,=1、2、3
φ—— 雷诺应力输运方程压力应变相,Pa/s,,=1、2、3
,,ρ—— 分别为流体、混合相密度、相颗粒密度,kg/m
μ,α ρ—— 分别为流体黏度、第相流体黏度,Pa·s
