基于线性二自由度模型的多轴车辆转向特性仿真

李正，刘相新，黎兰

(北京航天发射技术研究所，北京 100076)

重型多轴车辆一般是指轴数≥3的越野车辆，包括驱动形式为6×6、8×8、10×8、12×10、12×12、16×10、16×16等全轮或非全轮驱动车辆[1]。重型多轴车辆具有载重能力大、通过能力强等突出特点，在军民用领域都应用广泛，如作为地空导弹、岸舰导弹、地地导弹、战略导弹等武器装备的机动平台或大吨位起重机的机动平台等。由于多轴车辆的转向系统结构复杂，并且对车辆机动性的影响极大，因此需要开展转向特性研究。刘芹芹[2]推导了多轴车辆非线性二自由度动力学模型，提出了基于理想模型跟踪的非线性多轴车辆控制。黄薇等[3]建立了某三轴特种车辆的多体动力学模型，分析了该车辆的操纵稳定性。韩汪利[4]基于零质心侧偏角控制策略，结合电液比例转向技术对某型号五轴全路面起重机进行了仿真分析。陈翔[5]提出了4种阿克曼等效转向模型，并基于第三种阿克曼等效转向模型，提出了以车辆操纵稳定性和轮胎磨损为控制目标的分层转角控制策略。姚广磊等[6]研究了某三轴车辆的5种转向模式的稳态和瞬态响应特性及其应用范围。

车辆自动驾驶主要涵盖感知、规划和控制三大部分。线控转向作为控制层的重要组成部分，国内已有大量研究。施国标等[7]研究了四轮线控转向系统的横摆角速度反馈控制策略，改善了传统四轮转向的转向不足劣势，提高了操纵稳定性。陈小兵等[8]基于线控转向系统动力学模型，提出了一种横摆角速度和侧向加速度综合反馈的主动转向控制策略。张庭芳等[9]提出了最优滑模面的滑模控制算法，并以七自由度整车动力学模型为对象进行了仿真分析。王天怡[10]针对四轮线控转向稳定性与灵活性，提出了最优控制及比例控制。目前，线控转向的研究对象通常是两轴乘用车，针对多轴车辆的线控转向控制研究相对匮乏。

本文采用基于模型的研究方法，建立符合多轴车辆转向特性的数学模型，并对建立的数学模型进行仿真分析，以定性地掌握车辆转向过程中所表现出来的物理特性，为后续转向控制器设计提供理论依据。

1 多轴车辆线性二自由度模型

多轴车辆转向动力学模型从经典的线性二自由度模型拓展得到。线性主要指忽略轮胎侧偏的非线性特性；而二自由度是指在对车辆转向特性进行分析时，仅考虑车辆的y向位移(横向车速)和绕z轴转动的角度(横摆角速度)。

1.1 坐标系定义

为表述清楚，首先对车辆坐标系予以说明，见图 1。其中，坐标原点设在车辆质心位置, 各个方向规定如表1所示。绕x轴的侧倾角速度、绕y轴的俯仰角速度、绕z轴的横摆角速度正方向采用右手定则确定。此外，还需要对车轮坐标系予以说明，见图 2。垂直于车轮旋转轴线(忽略主销倾角，假设与地面垂直)的轮胎中心平面称为车轮平面。坐标原点设在车轮平面和地平面的交线与车轮旋转轴线在地平面上投影线的交点，各个方向规定如表2所示。

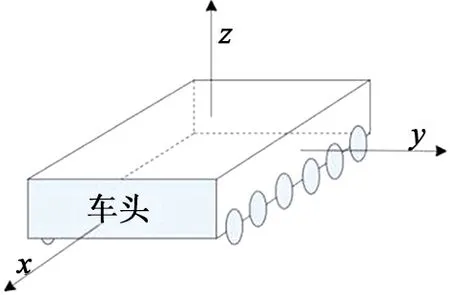
图1 车辆坐标系Fig.1 Vehicle coordinate system

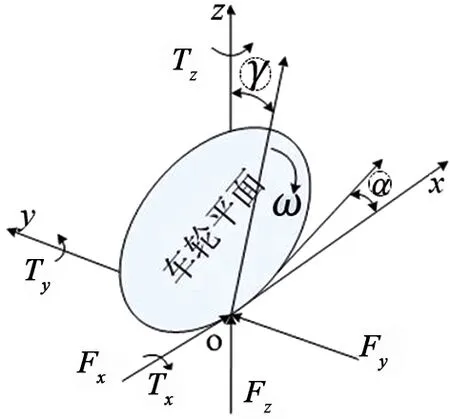
图2 车轮坐标系Fig.2 Wheel coordinate system

表1 车辆坐标系参数及其含义Table 1 Vehicle coordinate system parameters and their meanings

表2 车轮坐标系参数及其含义Table 2 Wheel coordinate system parameters and their meanings

1.2 模型假设

建立线性二自由度模型的假设包括：

(1)忽略实际转向系统的影响，将前轮转角作为模型输入；

(2)忽略悬架的影响，车辆始终平行于地面运动，即z向位移、绕x轴的侧倾角和绕y轴的俯仰角均为0；

(3)轮胎侧偏特性位于线性范围内，车辆侧向加速度不超过0.4g；

(4)仅考虑地面侧向反作用力对轮胎侧偏特性的影响，忽略地面切向反作用力对轮胎侧偏特性的影响；

(5)不考虑空气阻力的影响；

(6)忽略载荷变化对左右车轮的影响；

(7)忽略回正力矩的影响；

(8)车速(x向速度)视为不变，忽略加减速时载荷转移的影响。

在以上假设的作用下，车辆被简化成了一个单侧模型，如图3所示。通过该简化模型进行转向特性分析，会有以下几点主要影响：当侧向加速度超过0.4g时，轮胎侧偏呈现出明显的非线性特性，该简化模型失效；没有考虑前后、左右的载荷转移，仅适合较为平稳的转向过程；没有考虑道路坡度及车辆悬架对转向特性的影响。

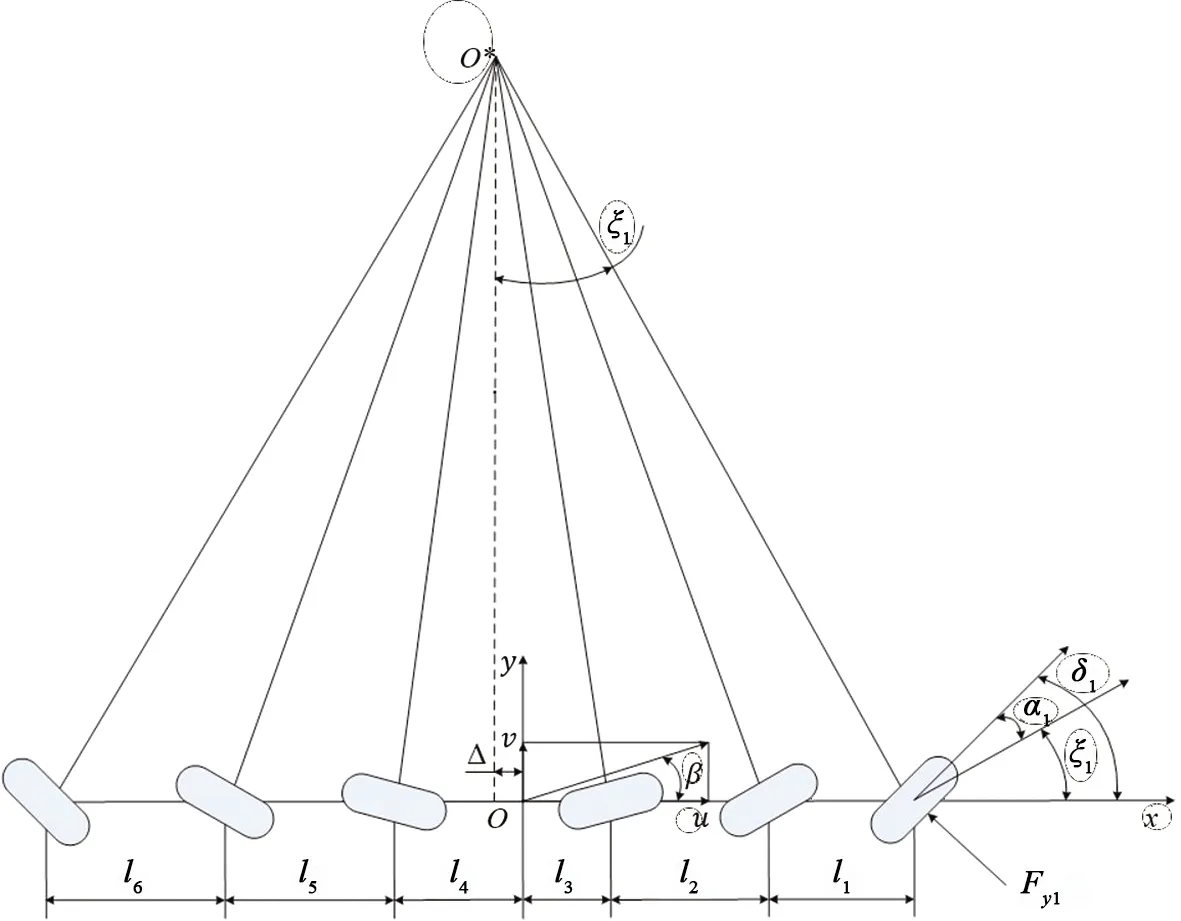
图3 线性二自由度多轴车辆模型Fig.3 Linear 2-DOF multi-axle vehicle model

该简化模型虽然存在一定的局限性，但是对于小坡度道路上的平稳转向过程具有很好的适用性。同时，简化模型也有利于降低后续转向控制器的设计难度。

1.3 车轮侧偏特性

由以上假设可知轮胎侧偏特性在线性范围内，即

Fyi=kiαi，

(1)

其中，Fyi为第i轴车轮受到的地面侧向反作用力(即侧偏力)，ki为第i轴车轮侧偏刚度之和，αi为第i轴车轮的侧偏角。

通过图3 可以发现侧偏角与车轮转角的关系，即αi=δi-ξi。同时，应该注意到在车轮坐标系的定义中，这个侧偏角是负的。因此，实际侧偏角为

αi=-(δi-ξi)，

(2)

其中，δi为第i轴车轮的转角，ξi为第i轴车轮速度与x轴的夹角。

结合质心侧偏角的定义，式(2)可写为

(3)

即得到车轮侧偏特性：

(4)

其中，β为质心侧偏角，li为第i轴到车辆质心的距离，ωr为车辆横摆角速度，u为车辆质心速度在车辆坐标系x轴上的分量。

1.4 整车动力学方程

将车辆的绝对加速度(相对于地面参考系)沿车辆坐标系的x轴、y轴分解，再列出沿y轴方向的力平衡方程和绕z轴方向的力矩平衡方程：

(5)

代入车轮侧偏特性，整理后可得线性二自由度多轴车辆转向动力学方程：

(6)

其中，m为车辆总质量，Iz为车辆绕z轴的转动惯量。

2 多轴车辆线性二自由度模型

为定性分析，考虑以下三种情况：

(1)仅前两轴转向，即ε=[1 1 0 0 0 0]；

(2)前两轴转向、后两轴负转向，即ε=[1 1 0 0 -1 -1]；

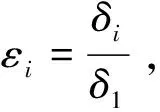
2.1 稳态横摆角速度增益

采用Matlab绘制三种情况下的稳态横摆角速度增益，见图4。从图4可以看出，三种情况下的稳态横摆角速度增益均随着车速增加而增大。后两轴负转向时增益增大的速度最快，相同车速下增益值最大。仅前两轴转向次之。后两轴正转向时增益增大的速度最慢，相同车速下增益值最小。从物理意义上分析，稳态横摆角速度增益越大，表现出来的是车辆转向越容易、转弯半径越小。而增益增大的速度越快，说明车速增加对车辆转向的影响程度越明显。

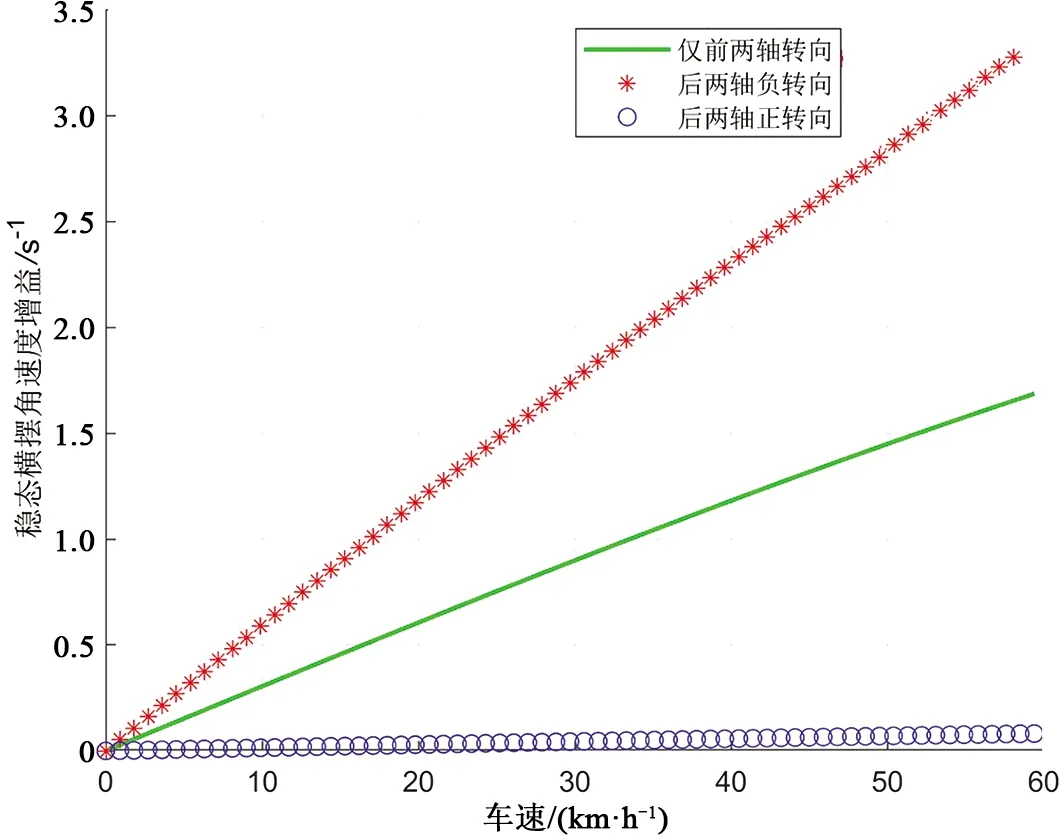
图4 三种情况下的稳态横摆角速度增益Fig.4 Steady-state yaw angular velocity gain in three cases

2.2 稳态质心侧偏角增益

采用Matlab绘制三种情况下的稳态质心侧偏角增益，见图5。从图5可以看出，三种情况下的稳态质心侧偏角增益都随着车速增加而逐渐减小。后两轴负转向时增益减小的速度最快，相同车速下增益值最小。仅前两轴转向次之。后两轴正转向时增益减小的速度最慢，相同车速下增益值最大。由车轮侧偏特性可知，随着质心侧偏角的减小，各轴车轮的侧偏角也会随之减小，这意味着侧偏角对转向的影响程度逐渐减小，也意味着转向半径越来越小、转向灵活性越来越高。

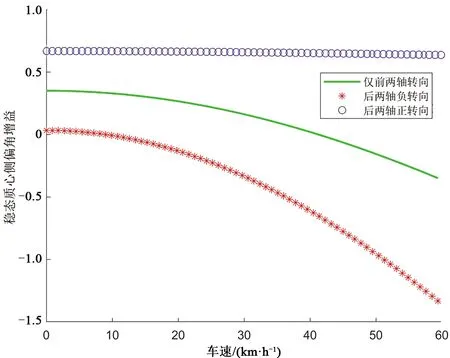
图5 三种情况下的稳态质心侧偏角增益Fig.5 Steady-state centroid sideslip angle gain in three cases

综上所述，如果将仅前两轴转向时车辆转向的难易程度视为“中等”，那么后两轴负转向时车辆转向的难易程度则可以视为“简单”，而后两轴正转向时的转向难易程度则可以视为“困难”。对于两轴车辆而言，由于其轴数少、车身短，车辆具有“中等”转向难易度就可以满足转向机动性要求。而对于多轴车辆而言，由于其轴数多、车身长，“中等”转向难易度则无法满足车辆转向性能要求。因此，需要采用多轴转向技术来实现“简单”的转向难易程度。

3 转向过程瞬态特性分析

为定性分析，考虑以下三种情况：

(1)仅前两轴转向，即ε=[1 1 0 0 0 0]；

(2)前两轴转向、后两轴负转向，即ε=[1 1 0 0 -1 -1]；

(3)前两轴转向、后两轴正转向，即ε=[1 1 0 0 1 1]。

3.1 横摆角速度阶跃响应

采用Matlab绘制车速为5、30、60、90 km/h时三种情况下的横摆角速度阶跃响应曲线。从图6可以发现，无论是低速、中低速、中高速还是高速，三种情况下的阶跃响应曲线均表现出了相同的趋势。后两轴负转向时的横摆角速度稳态值最大，仅前两轴转向次之，后两轴正转向时的横摆角速度稳态值最小。这与稳态特性分析结果相吻合，即后两轴负转向可以增强转向灵活性。

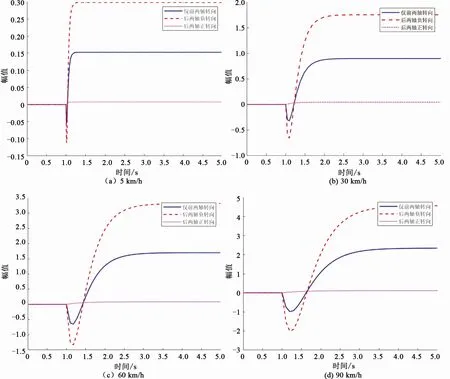
图6 横摆角速度阶跃响应曲线Fig.6 Step response curve of yaw angular velocity

3.2 质心侧偏角阶跃响应

采用Matlab绘制车速为5、30、60、90 km/h时三种情况下的质心侧偏角阶跃响应曲线。从图7可以看出，低速和中低速时，三种情况下的质心侧偏角稳态值最终趋于相同的正值。而中高速和高速时，三种情况下的质心侧偏角稳态值最终趋于相同的负值。值得关注的是，在低速和高速时，三种情况下的质心侧偏角阶跃响应曲线相差甚微。只有在中低速、中高速时，三者体现出了较大的差异，后两轴负转向和仅前两轴转向表现出过阻尼特性，而后两轴正转向表现出欠阻尼特性。因此理论上，采用后两轴正转向能够提高转向稳定性。

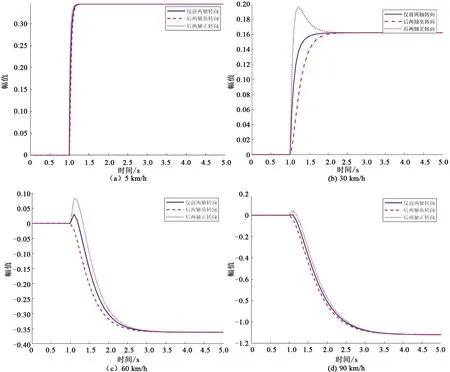
图7 质心侧偏角阶跃响应曲线Fig.7 Step response curve of centroid sideslip angle

4 结论

通过经典的前轮转向动力学模型，拓展得到了多轴车辆转向动力学模型。依据该模型，采用Matlab对仅前轴转向、前后轴负转向和前后轴正转向进行了仿真分析，定性地研究了转向过程稳态特性和瞬态特性。其中，稳态仿真结果和瞬态仿真结果都定性地说明了采用多轴转向(前后轴负转向)能够有效提升转向机动性。同时，应当注意到中高速时车辆转向过于灵活会对行驶稳定性产生较大影响，需要采取转向桥组锁止等策略来提升行驶稳定性。

该模型为后续转向控制器设计提供了有力的理论支撑，但考虑到多轴车辆车身长、轴数多、载荷大等特点，下一步应当将该模型从单侧模型扩展为整车模型。同时，还需要建立具备更高自由度的转向模型或非线性模型来与之对比。除此之外，由于低速和高速时三种转向情况下的质心侧偏角阶跃响应相差不大，因此可以在控制策略中加入横摆角速度增益和质心侧偏角增益的变权重控制，通过智能算法优化两者对转角的影响程度，从而进一步提高车辆的转向机动性与稳定性。