考虑出行全过程的城市群多方式交通流分配模型与算法

徐璞

(1.北京交通大学 交通运输学院，北京 100044；2. 中铁工程设计咨询集团有限公司，北京 100055)

中国城市群发展已进入快车道，“十三五”规划纲要提出，要建设京津冀、长三角、珠三角等19个城市群。今后较长时期内，以城市群为主体形态的城际客运量将大幅增长，为满足城市群内部旅客运输需求，迫切需要多种交通方式并存的交通网络结构作为支撑。结合城市群旅客出行特征，研究网络达到均衡状态时的交通流量分布状态，已经成为确定城市群交通方式合理发展规模、优化城市群交通网络结构、建设城市群综合交通运输体系的重要依据。

对于城市交通系统而言，无论是单方式还是多方式，交通网络结构是进行交通系统分析的前提和基础。目前，国内外对于城市单一方式网络拓扑结构的描述已经比较成熟，这些研究大都以图论为基础，将单一方式的路网转化成由点和边组成的网络结构。但是随着城市交通方式的多样性发展，交通网络结构也变得越来越复杂，简单的网络拓扑结构已经不能够描述复杂的多方式交通系统，因此越来越多的学者开始研究多方式交通系统的网络拓扑结构。国内外一些学者基于地理信息系统(geographic information system，GIS)对多方式交通网络的建模做了一些研究[1-2]。虽然这些基于GIS技术建立的网络拓扑结构能够很好地描述道路网络的特征，但不能描述多方式交通网络中不同交通方式之间相互独立而又联系的特征。Chen等[3]、Si等[4]和Shan等[5]用一种分层网络结构描述城市多方式交通系统，在这种结构中，每一层都代表一种交通方式的运行网络，这种结构可以很好地描述每种交通方式的运行特征，但是不能描述不同方式之间的关联关系。此外，Lozano等[6-7]基于超网络理论为城市多方式交通系统建立了超网络，这是由多层独立网络集结而成的网络，每一层独立网络都是某一种交通方式的运行网络，这种网络不仅能够表达每种交通方式网络独立运行的特征，还能够描述不同交通方式之间的联系。在此基础上，李红莲[8]、汪勤政等[9]和周豪等[10]基于多方式交通超网络，研究了可换乘条件下的城市交通系统。

本文通过对城市群旅客出行过程的充分分析，运用网络拓扑结构构建与之对应的多方式交通系统超网络模型，以此对城市群交通系统进行描述，并根据网络结构特性和出行者换乘行为特征给出网络中有效路径的具体搜索算法。同时提出多模式交通网络条件下的Logit-SUE 模型，并基于相继平均法对模型进行求解，以此为依据对城市群多方式交通超网络上的流量分布状态进行研究分析。

1 城市群旅客出行过程及交通网络模型

1.1 城市群旅客出行定义及过程

城市群出行是旅客为了实现某一生活、生产目的，采用某一种或几种交通工具，经由城市道路、城际交通运输线路，从城市群内的一个城市的某一地点出发到城市群中另一个城市的某一地点，并沿单方向移动的全过程。城市群旅客出行不仅仅包含城市(镇)之间的出行，还必须要与两端的城市(镇)内部出行进行衔接才能完成，因此对城市群出行的研究，应该从城市群旅客出行的整个过程出发，综合考虑旅客从出发地到目的地的全过程，整体把握其出行规律。城市群旅客出行全过程如图1所示。

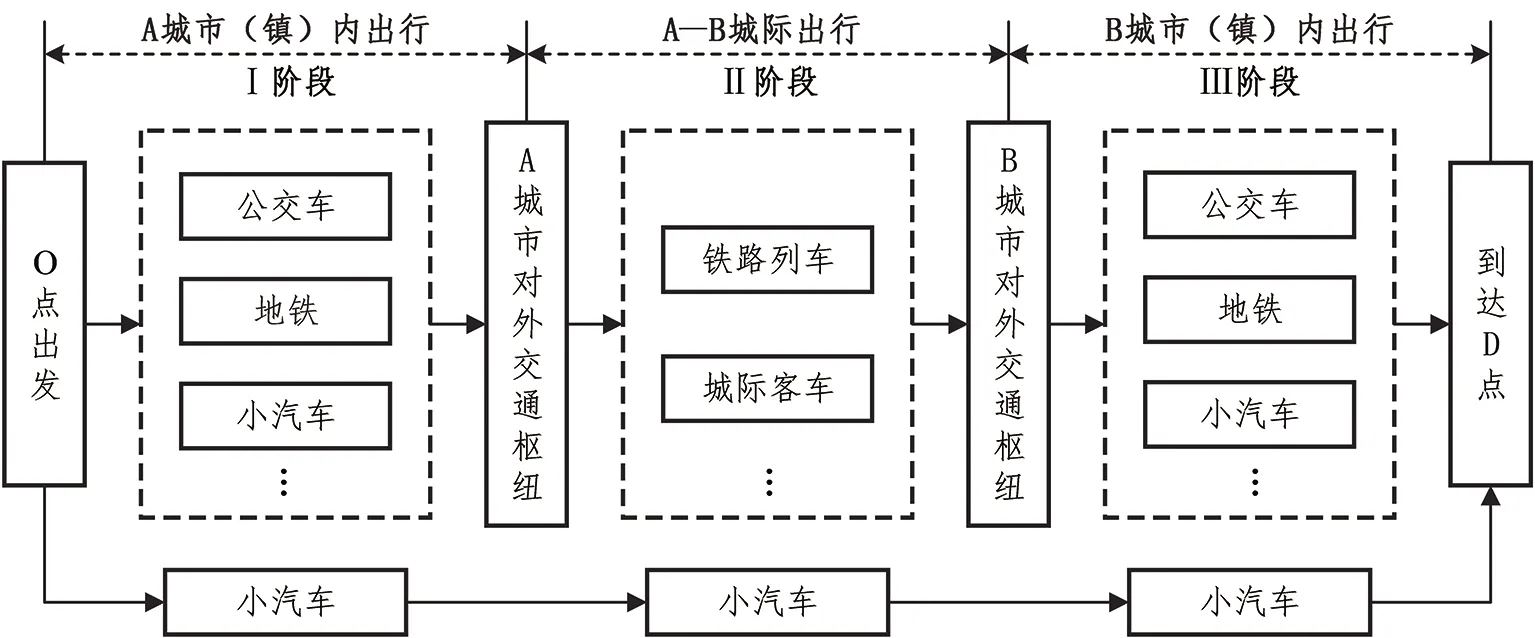
图1 城市群旅客出行全过程Fig.1 The entire process of passenger travel in an urban agglomeration

城市群旅客出行全过程分为三阶段：Ⅰ阶段为在出发地城市的市内出行，旅客从A城市某交通小区内的出发点，乘坐某种交通方式，经由城市交通网络到达该城市的某一对外交通枢纽；Ⅱ阶段为城市群中A城市至B城市的城际出行，旅客采用某一种城际交通方式，从A城市的对外交通枢纽，经由城际交通运输网络，到达目的地B城市的对外交通枢纽；Ⅲ阶段为在目的地城市的市内出行，旅客从B城市的对外交通枢纽，乘坐某种交通方式，经由城市交通网络，到达该城市某交通小区内的目的地。

1.2 城市群多方式交通超网络模型

与城市群旅客出行过程相对应，城市群交通系统是一个包含起讫点城市内部主干交通网络、城际交通网络的多种交通方式叠加的多层级交通网络，而每一层级的交通网络又是由多种交通方式的子网络复合而成的。从逻辑网络的角度来看，城市群交通网络是由城市内部、城市间不同交通方式的逻辑子网络构成的，将不同层次、不同方式的交通网络通过实际的换乘关系建立联系，就形成了城市群交通系统的超级网络。出行者完成一次城市群出行一般包括上网过程、行驶过程、换乘过程和下网过程4个阶段，根据出行者的出行特征，本文构建一种超网络结构来描述城市群交通系统。在超网络结构中，城市内部主干交通网络与城际交通网络通过城市对外交通枢纽的换乘节点连接，同时，城市内部主干交通网络和城际交通网络均由多方式子网构成，因此，超网络(ES)是一个由多层次、多方式子网络构成的系统，可以表示为：

ES=(N,A,M)，

(1)

N=N1∪N2，

(2)

A=A1∪A2∪A3∪A4，

(3)

A2=Au∪Ai，

(4)

M=Mu∪Mi，

(5)

式中：N表示超网络中所有节点的集合；A表示超网络中路段的集合；M表示超网络中交通方式的集合；N1表示起讫点的集合，N2表示除起讫点之外的节点集合；A1、A2、A3、A4分别表示上网路段集合、行驶路段集合、换乘路段集合和下网路段集合，其中行驶路段包括城市路段Au和城际路段Ai；Mu表示城市内部交通方式的集合，Mi表示城际交通方式的集合。

下面通过一个示例来说明城市群交通系统结构。图2为某城市群内部从A城市到B城市的城市群交通网络示意图。出发地O是A城市的某一居住区，目的地D是B城市的某一商务办公区。出行者从A城市的出发地到B城市的目的地，可选择的市内交通方式有小汽车、公交车和地铁，分别用数字1、2、3表示， {1,2,3}∈Mu，可选择的城际交通方式有小汽车、铁路和城际客车，分别用c、t、b表示，{c,t,b}∈Mi。出行者可以从对外交通枢纽由城市交通网络换乘到城际交通网络，或从城际交通网络换乘到城市交通网络，节点3和10分别是A、B城市的小汽车对外枢纽，节点5和14分别是A、B城市的铁路对外枢纽，节点9和16分别是A、B城市的城际客车对外枢纽。

图2 城市群多方式交通出行网络示意图Fig.2 Schematic diagram of multi-modal transportation travel network of urban agglomeration

根据图2所示的城市群交通系统构建城市群多方式交通超网络，如图3所示。本文将图3超网络中从A城市的出发地到B城市的目的地的路径称为超路径，每一条可行超路径的换乘次数为2次，即由起点城市的某种交通方式换乘到某种城际交通方式，再由某种城际交通方式换乘到讫点城市的某种交通方式。通常情况下，起讫点之间会存在多条可行超路径，然而，并不是所有的可行超路径都会被出行者所考虑，本文基于出行者可承受的广义出行费用，将满足式(6)的路径称为有效超路径。

(6)

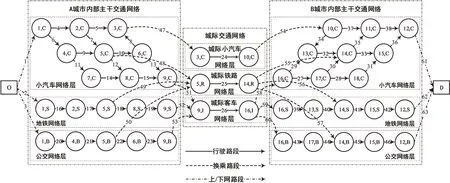
注：C表示小汽车；S表示地铁；B表示公交车；R表示铁路；I表示城际客车。图3 城市群多方式交通超网络Fig.3 Super network of multi-modal traffic in an urban agglomeration

2 广义出行费用

从城市群旅客出行的全过程考虑，将上述超网络模型的路段分为上网路段、行驶路段、换乘路段和下网路段。出行者在不同路段上的出行活动差异导致各类路段上的广义费用定义不同。本文考虑时间成本、货币成本和舒适度损耗对出行费用的影响，对不同类型路段的广义费用进行定义。

2.1 上网路段

上网路段的费用是出行者从出发地到达城市交通网络站点的上网时间费用。对于小汽车出行者来说，上网时间主要是在上网路段的行驶时间。对于地铁和公交车出行者来说，上网时间主要是到达站点的步行时间和在站点的等待时间。上网费用可以表示为：

(7)

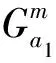
(8)

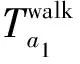
2.2 行驶路段

行驶路段包括城市内部交通网络上的车辆行驶路段和城际交通网络上的车辆行驶路段。对于城市内部交通网络上行驶路段的广义费用突出考虑交通拥挤的时间费用，对于城际交通网络上行驶路段的广义费用突出时间费用、货币费用以及舒适度损耗。

2.2.1 城市交通网络上的行驶路段

小汽车在路段上的时间费用可以通过BPR函数来确定，其货币费用主要是燃油费。假设公交车和地铁在路段上的行驶时间是固定的，但考虑交通拥挤导致的路段出行时间延长，其时间费用同样仿照BPR函数来确定，相应的货币费用主要是线路票价，本文假设地铁和公交车都采用单一票价。城市交通网络上行驶路段的费用可以表示为：

(9)

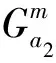
(10)

(11)

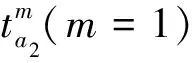
2.2.2 城际交通网络上的行驶路段

对于小汽车来说，时间费用同样通过BPR函数来确定，相应的货币费用主要是燃油费和通行费。对于城际列车和城际巴士来说，假设其严格按照运营时刻表运行，运行时间确定，但是由于乘客数量的增加会使得舒适感降低，从而感知出行时间延长，因此要对行驶时间进行放大来表示舒适度损耗，相应的城际列车和城际巴士的货币费用为路段票价。城际交通网络上行驶路段的费用可以表示为：

(12)

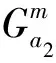
(13)

(14)

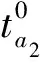
(15)

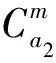
2.3 换乘路段

换乘路段的费用是出行者在城市交通网络与城际交通网络之间进行换乘产生的费用，包括换乘时间和换乘造成的舒适度损耗两部分。换乘时间由出行者在换乘路段上的步行时间和不同交通方式之间的换乘等待时间构成，舒适度损耗与换乘时间有关，时间越长，舒适度损耗越高。换乘路段的费用可以表示为：

(16)

(17)

(18)

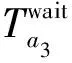
2.4 下网路段

下网路段的费用是出行者从城市交通网络站点到达目的地的下网时间费用。对于小汽车出行者来说，下网时间是下网路段的行驶时间。对于地铁和公交车出行者来说，下网时间是下网到达目的地的步行时间。下网费用可以表示为：

(19)

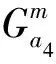
(20)

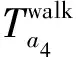
本文将超路径的费用定义为组成该路径所有路段费用的叠加，其表达式为：

(21)

3 随机用户平衡分配模型

本文提出如下随机平衡分配模型来描述多方式交通网络中的流量分配问题。

(22)

(23)

(24)

(25)

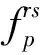
可以证明，模型式(22)～(25)的最优解满足式(26)所示的Logit流量分布条件[8]。

(26)

4 求解算法

可采用相继平均法(method of successive average，MSA)对模型进行求解，具体步骤如下：

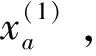
在上述算法中的Step2和Step3中需要确定有效路径的集合，依据式(6)对有效路径判定条件的定义，本文基于图的遍历算法提出有效路径搜索算法来确定有效路径的集合：

在以下有效路径搜索算法中：r表示网络的起点；s表示网络的终点；s(i,j)是换乘路段的判定值，如果路段(i,j)是换乘路段，其值为1，如果路段(i,j)不是换乘路段，其值为0；U(r,i)为由r至i的换乘次数；Umax表示最大换乘次数；a(i)表示沿某条遍历路径到达节点i且最靠近i的节点。

Step1 初始化，令U(r,i)=0，a(i)=0，输入Umax和σ的值。

Step4 如果s(i,j)=1，判断是否满足s(a(i),i)=1，若是，转Step7；若否，令U(r,i)=U(r,a(i))+s(a(i),i)，转Step5；如果s(i,j)=0，转Step6。

Step5 如果U(r,i)≤Umax，转Step6；否则转Step7。

Step6 判断节点j是否为终点s，若是，记录该条有效超路径；若否，设节点j为当前节点，转Step3。

Step7 利用回溯的方法返回到上一层，若未退至起点，转Step3。

有效超路径搜索算法的Step2中，需要对最短可行超路径进行确定，本文通过如下基于Dijkstra算法的最短可行超路径搜索算法确定最短可行超路径：

在以下最短可行超路径搜索算法中,q(i)表示沿着最短路径到达节点i且与i最靠近的节点,w(i,j)为路段(i,j)的阻抗,d(i)为由r沿最短路径至i的最小阻抗,In为第n步的临时标号节点集合,Fn为第n步的永久标号节点集合,l为最新得到的永久标号点。

Step1 初始化，令n=0，F0={r}，I0为除r以外所有节点的集合，d(r)=0，l=r，q(r)=0，d(i)=∞∀i≠r，q(i)=0，U(r,i)=0。

Step2 检查l的邻接节点，如i，其中i∈In，判断i是否被检查过，若否，转Step3；若是，检查下一个节点，转Step3。

Step3 检查路段(l,i)，若s(l,i)=0，转Step4；若s(l,i)=1，判断是否满足s(q(l),l)=1，若是，转Step2；若否，判断是否满足U(r,i)≤Umax，若是，转Step4；若否，转Step2。

Step4 若d(i)>d(l)+w(l,i)，令d(i)=d(l)+w(l,i)，q(i)=l,否则令d(i)和q(i)不变；若将l的邻接点检查完毕，转Step5,否则转Step2。

Step5 从节点l的全部邻接节点i中，找出d(i)最小的节点，如节点j，令l=j，U(r,l)=U(r,q(l))+s(q(l),l)，Fn+1=Fn∪{l}，In+1=In-{l}，n=n+1，转Step6。

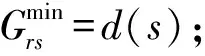
5 算例分析

以图2所示的城市群多方式交通出行网络为例,对模型与算法进行验算，本文主要模拟计算的过程，对参数的精确性要求不高，参数取值如下：

(1)ps=0.6 元/km；p2=1 元；p3=2 元；r24=10 元；q=5000 人；v=10 元/h；pt=50 元；pb=30 元。

(2)σ=0.5；Umax=2；γ=0.2；b=0.1；c=0.2；η=0.8；θ=1；α=0.15；β=4；α1=0.15；β1=4；α2=α3=0.1；β2=β3=2；ε=0.001。

各方式的路段出行信息如表1～6所示。

表1 城际交通方式出行信息Table 1 Travel information of intercity transportation modes

表2 地铁出行信息Table 2 Travel information of subway

表3 公交车出行信息Table 3 Travel information of bus

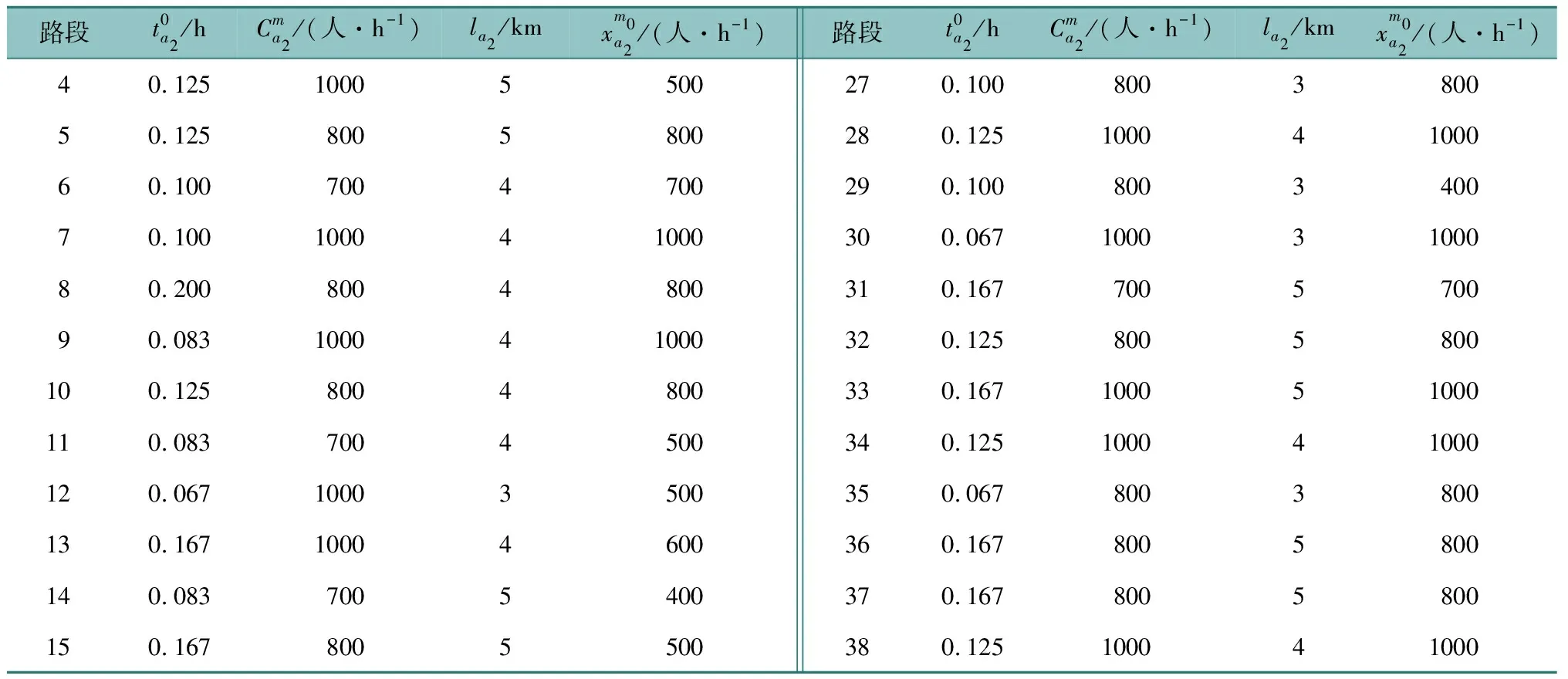
表4 小汽车出行信息Table 4 Travel information of car

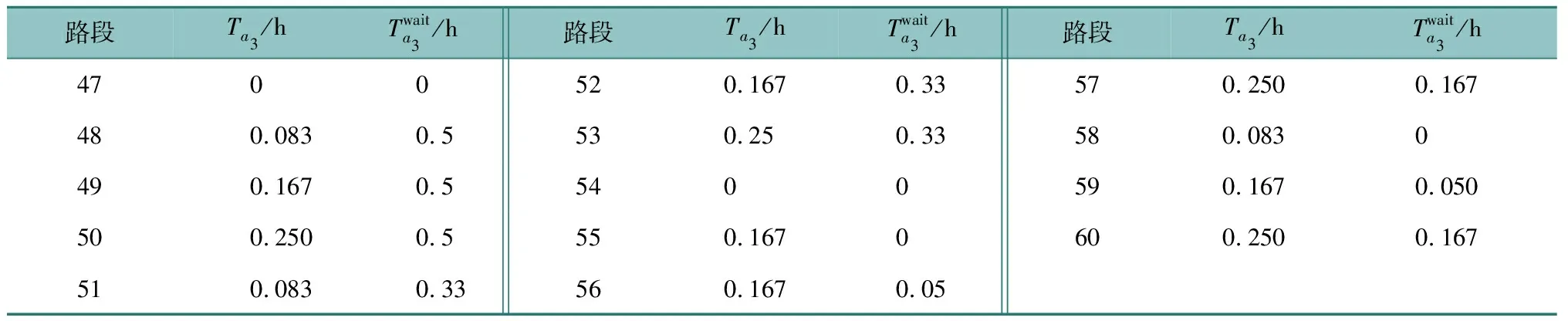
表5 换乘路段出行信息Table 5 Travel information of transfer links

表6 上/下网路段出行信息Table 6 Travel information of boarding/alighting links

首先对MSA算法的收敛性进行分析，通过每次迭代中上网路段1和下网路段62上的流量变化来表示算法的收敛性，图4给出了在总需求一定的情况下MSA算法的收敛情况。可以看出，算法具有明显的收敛性质，在迭代59次后，所求解达到了收敛要求。

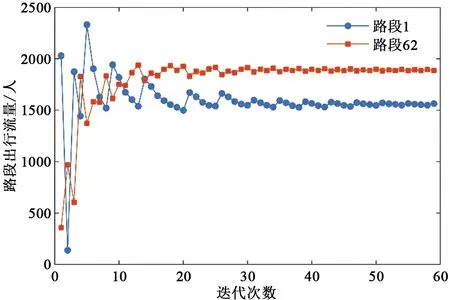
图4 算法的收敛性Fig. 4 Convergence of the algorithm

对于算例中的超网络，经程序计算，达到平衡时，超网络中的有效超路径共有74条。图5显示了超网络达到平衡时各路段的出行流量，可以看出，对于各种出行模式中城际交通方式的选择情况，有18.9%的出行者选择小汽车，有57.1%的出行者选择城际列车，有24%的出行者选择城际客车。

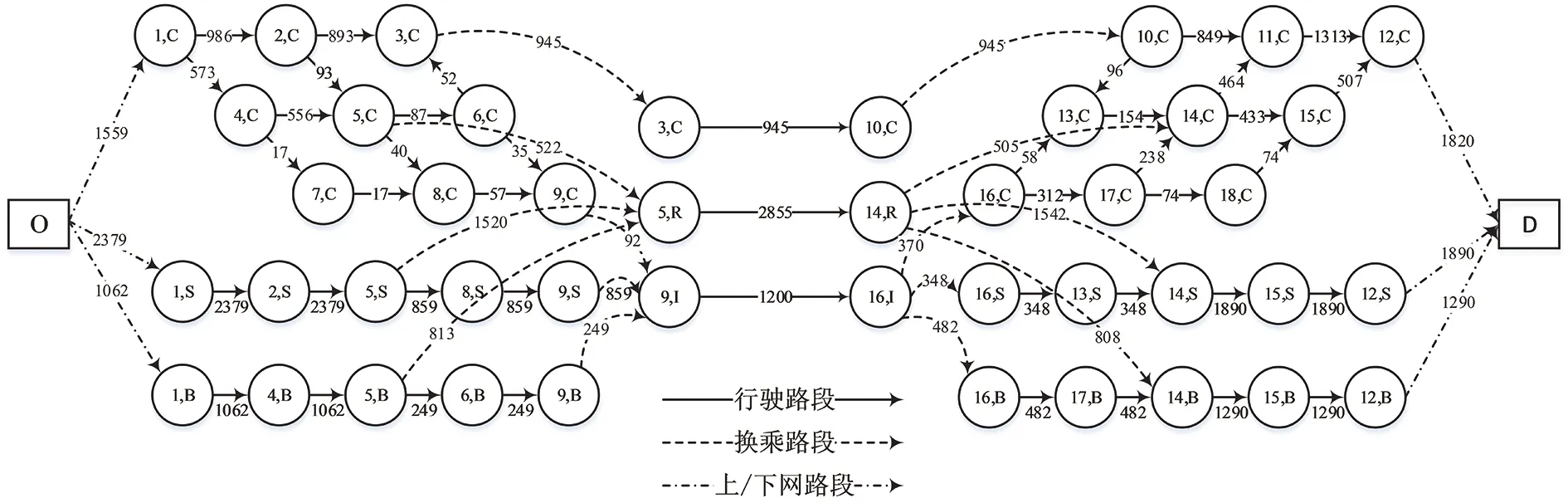
图5 超网络路段流量分配结果Fig. 5 Traffic assignment result of super network

6 结论

本文基于对城市群旅客出行全过程的分析，构建了包含起讫点城市内部主干交通网络及城际交通网络的城市群多方式交通超网络，以此作为研究城市群多方式交通分配问题的网络模型。通过超网络模型，多方式交通系统的分配问题可以很容易地转化为一般网络的交通分配问题。研究结果表明，本文提出的模型和算法是可行有效的，并且说明在对城市群城际交通网络进行优化分析时，不能仅从各种城际交通方式自身的角度出发分析问题，而应当从城市群旅客出行全过程以及多方式交通系统的角度进行具体分析。